三角形重心、垂心、内心、外心的向量性质及简单应用
2019-04-13广东省珠海市斗门区第一中学519100陈水松
广东省珠海市斗门区第一中学(519100) 陈水松
一、三角形四心的表述与性质
(一)重心——三角形三条边上的中线的交点叫做三角形的重心.重心将中线长度分成2: 1 的两部分.
证法1设O(x,y), A(x1,y1), B(x2,y2), C(x3,y3),是△ABC 的重心.
证法2如图1,因为所以所以A、O、D 三点共线, 且O 分AD 为2:1,所以O 是△ABC 的重心.
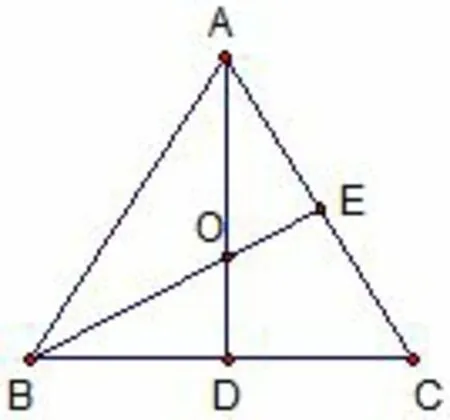
图1
2.若O 是△ABC 的重心, 则S△BOC= S△AOC=
证明由所以(反之也然)故O 为△ABC 的重心.
(二)垂心——三角形三条高线的交点叫做三角形的垂心.
证明如图2 所示H 是三角形ABC 的垂心, BE 垂直AC,AD 垂直BC,D、E 是垂足.同理为△ABC 的垂心.
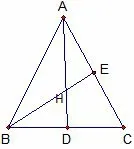
图2
(三)内心——三角形三个内角的角平分线的交点叫做三角形的内心,即三角形内切圆圆心.
⇔O 为△ABC 的内心.
⇔O 为△ABC 的内心.
证 明因 为所 以所 以所以
证明因为O 为△ABC 的内心, 故所以
(四)外心——三角形三条边上的中垂线的交点叫做三角形的外心,即三角形外接圆圆心.
2.若O 是△ABC 的外心, 则S△BOC: S△AOC:S△AOB= sin ∠BOC : sin ∠AOC : sin ∠AOB = sin 2A :sin 2B :sin 2C.
证明设△ABC 外接圆半径为R, 则S△BOC=, S△AOC=sin ∠AOC, S△AOB=又∠BOC = 2A,∠AOC = 2B,∠AOB =2C, 所 以S△BOC: S△AOC : S△AOB = sin ∠BOC :sin ∠AOC :sin ∠AOB =sin 2A:sin 2B :sin 2C.
二、应用举例
例1 O 是平面上一定点,A、B、C 是平面上不共线的三个点,动点P 满足λ ∈[0,+∞),则点P 的轨迹一定通过△ABC 的( )
A.外心 B.内心 C.重心 D.垂心
解析如图3 所示△ABC,D、E 分别为边BC、AC 的中点.因为所以因为所以所以所以点P 的轨迹一定通过△ABC 的重心,即选C.

图3
例2O 是平面上一定点, A、B、C 是平面上不共线的三个点, 动点P 满足λ ∈[0,+∞),则点P 的轨迹一定通过△ABC 的( )
A.外心 B.内心 C.重心 D.垂心
解析因为分别为方向上的单位向量,所以平分∠BAC,所以点P 的轨迹一定通过△ABC 的内心,即选B.
例 3O 是 平 面 上 一 定 点, A、B、C 是 平 面上不共线的三个点, 动点P 满足λ ∈[0,+∞), 则点P 的轨迹一定通过△ABC 的( )
A.外心 B.内心 C.重心 D.垂心
解析如图4 所示AD 垂直BC,BE 垂直AC,D、E 是垂足.所以点P 的轨迹一定通过△ABC的垂心,即选D.
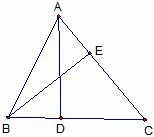
图4
例4(2018 ·重庆三模)已知点I 为△ABC 的内心,AC = 2, BC = 3, AB = 4, 若则x+y =____.
解析因为点I 为△ABC 的内心, 所以其中O 为任一点, a,b,c 为三角形三边.因此所以
例5(2016 ·福州质检)在△ABC 中, BC = 2,A = 45°, B 为锐角, 点O 是△ABC 外接圆的圆心, 则的取值范围是( )
解析由题意得取BC 的中点D,连接OD,AD,则OD⊥BC,所以= 4 sin2C -4 sin2B = 2 cos 2B-2 cos 2C = 2 cos 2B - 2 cos(270°- 2B)= 2 cos 2B +2 sin 2B =又45°<2B+45°<225°,所以所以即选A.
例6(2016·四川卷)在平面内,定点A,B,C,D 满足-2,动点P,M 满足则的最大值是( )
解法1由题意,因为所以D 到A,B,C 三点的距离相等,D 是△ABC 的外心.所以DB⊥AC.同理可得,DA⊥BC,DC⊥AB,从而D 是△ABC 的垂心,所以△ABC 的外心与垂心重合,因此△ABC 是正三角形,且D是△ABC 的中心,所以所 以 正 三 角形ABC 的边长为以A 为原点建立如图5 所示的平面直角坐标系, 则由设P 点的坐标为(cos θ,sin θ), 其中θ ∈[0,2π).由可知M 是PC 的中点, 所以M 的坐标为则当时,取得最大值
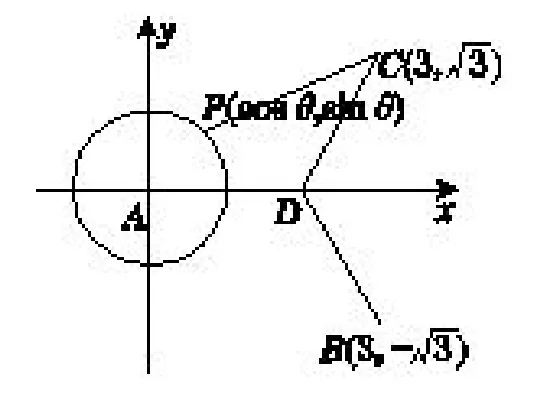
图5
解法2由可知D 为△ABC 的外心, 再根据得∠ADB = ∠BDC = ∠CDA = 120°, 于是△ABC为正三角形, 且边长为设AC 的中点为T, 则由条件知所以当且仅当即同向时等号成立.
例7点O 在△ABC 内部且满足则△ABC 面积与△AOC 面积之比是____.
解 法1取BC、AC 中 点D、E, 连OD、OE, 因为所以(2)+ (1)×2 得所以共线,且所以S△COE= 2S△COD, 所以S△COA=所以S△ABC:S△AOC=3:1.
解法2延长OB 至D, 使OB = BD; 延长OC 至E, 使CE = 2OC.则2OB = OD, 3OC = OE.因为所以O为△ADE 的重心, 所以所以S△ABC=S△AOC+S△BOC+S△AOB =S△ADE+=所以S△ABC:S△AOC ==3:1.
三、拓展延伸
1.(2018·皖江八校5 月联考)已知A,B,C 为圆O 上的三点,若圆O 的半径为2,则( )
A.-1 B.-2 C.1 D.2
2.(2018 ·唐山三模)在△ABC 中, 点G 满足若 存 在 点O, 使 得且则m-n=( )
A.2 B.-2 C.1 D.-1
3.(2018 ·扬州四模)在△ABC 中, AH 是底边BC上的高, 点G 是三角形的重心, 若AB = 2, AC = 4,∠BAH =30°,则
4.(2018·济南二模)已知△ABC 中,AB =4,AC =5,点O 为△ABC 所在平面内一点, 满足则=____.
