延迟退休会损害健康吗?
——基于对退而不休的研究
2019-04-12黄乾于丹
黄乾,于丹
(南开大学 经济学院/中国特色社会主义经济建设协同创新中心,天津 300071)
1 引言
根据第六次人口普查数据,我国城镇60~64岁和65~69岁老年人口的劳动参与率分别为24.30% 和15.49%,而发达国家同年龄段人口的劳动参与率为:美国(55.80% 和31.56%)、德国(55.83%和14.00%)、法国(26.80%和.90%)、意大利(32.57% 和8.43%)、瑞典(70.31%和21.84%)、日本(62.90% 和41.44%)、韩国(59.83%和45.50%)、OECD 国家(49.12%和25.03%)。可见,我国老年人口劳动参与率明显低于绝大部分发达国家,特别是60~64岁低龄老年人口的劳动参与率不到大部分发达国家劳动参与率的一半。通过积极的劳动力市场政策和延迟退休年龄政策,提高老年人的社会和经济参与程度,特别是劳动力市场的参与程度,积极开发老年人力资源,是我国应对人口老龄化严峻挑战的必然选择。但是,老年人健康状况是延迟退休年龄政策实施的前提,延迟退休不能以损害老年人健康为代价。
目前关于延迟退休政策的研究已经很多,但主要从就业与劳动力资源开发、养老金等角度展开,较少涉及健康问题,相关的退休与老年人健康研究主要有三种观点:
第一,退休对老年人健康产生显著负面影响。如Sahlgren(2012)使用欧洲11个国家的面板数据,分别利用配偶的特征以及法定退休年龄作为工具变量,并采取一系列方法克服内生性,发现退休对自评健康、心理与身体健康都有显著的负向影响,且短期影响不明显,长期影响越来越显著[1]。Barnay(2015)也认为相比就业而言,退休对健康的负向作用更加明显[2]。
第二,退休对老年人健康产生显著的正向影响。Bénédicte H.Apouey,Cahit Guven,Claudia Senik(2018)利用澳大利亚家庭微观数据实证研究了退休对健康的冲击,发现退休能显著提高健康水平[3]。一些研究发现,退休的积极健康效应主要来自退休后老年人的社会参与作用。Sirven and Debrand(2008)利用反事实分析法分析了社会参与对欧洲50岁以上老年人健康的影响,他提出两个观点:一是,当个体到达一定年龄后,其所相识的人群数量开始减少,参加其它的社会团体能够帮助其维持社会网络的规模;二是,退休会导致认知能力的下降,而退休后的社会参与能够促进大脑活动,从而阻止该进程,保护精神健康。通过实证研究,他证实了自己的观点,发现提高老年人社会参与有利于提高其健康水平,且能够减轻总体之间的健康不平等[4]。之后,两位学者又通过构建联合递归模型发现社会资本与健康之间存在互利的关系,健康水平较高的人有更高的倾向参与社会活动且更能从中受益(Sirven and Debrand,2011)[5]。国内学者近年来也对该问题进行了分析,发现老年人社会参与与健康之间存在互相影响的循环机制,一方面,健康状况较好的老年人更倾向于参加社会活动;另一方面,进行社会参与能够显著的提高老年人的健康水平[6-8]。
第三,退休对老年人健康的影响是不确定的。Bassanini and Caroli(2014)通过文献整理与分析,认为退休对健康的影响取决于退休决策是自身选择还是外在约束,如果某人退休后被迫继续工作以及由于失业造成的被迫停止工作对健康有不利的影响,而自愿退休则对健康有正向作用[9]。Andreas Kuhn(2018)利用德国数据研究发现,退休行为既可能通过减少不健康、风险高、损害大的工作而提高老年人的健康水平,也可能由于退休改变了日程生活规律、身体和精神活动而降低老年人的健康水平[10]。由于退休影响健康存在滞后效应,有些学者研究了退休对健康的短期和长期影响(Heller-Sahlgren,2017)[11]。Dusanee Kesavayuth(2018)利用10个欧洲国家的数据采用工具变量法实证研究了退休对健康行为的影响,发现退休增加了一些健康行为,同时也减少健康行为,而且性别、地区、工作类型之间存在较大差异[12]。雷晓燕等(2010)使用我国2005年1%全国人口抽样调查数据,利用断点回归设计(RD)发现在正常退休年龄(强制退休),退休对男性健康有显著的负面影响,对女性则没有影响,而提前退休(自愿发生)对男性和女性的健康都没有影响[13]。利用同样的方法,王存同、臧鹏运(2016)使用2010年中国综合社会调查数据,得出了相似的结论[14],而邓婷鹤、何秀荣(2016)则利用2012中国家庭追踪调查数据发现退休对个体身体健康没有影响,对心理健康有显著的正向影响,退休后压力减小、认知能力以及生活满意度的提升是心理健康改善的主要原因[15]。另一方面是,老年人退休后时间安排对健康的影响。
那么,通过延迟退休政策延长老年人在劳动力市场的工作时间对健康会产生怎样的影响?回答这个问题,既可以提高劳动者对延迟退休政策的理解和接受程度,也能促进延迟退休政策的完善,提高老年人健康水平,实现健康老龄化的目标。由于我国还没有正式实施延迟退休政策,不能直接评估其对健康的影响,但是考虑到我国目前有大批60岁以上退休老年人仍继续在劳动力市场就业(即退而不休),通过他们的就业行为与健康之间的因果关系可以间接反映未来延迟退休政策实施的可能健康效应,所以本文利用2011年中国健康与养老追踪调查数据,采用反事实分析方法实证研究老年人“退而不休”行为对健康的影响,在一定程度上模拟和评估我国延迟退休政策可能产生的健康后果。与已有文献相比,本文的边际贡献在于以下三个方面:一是通过退而不休对健康的影响考察了延迟退休政策对老年人健康的可能影响;二是以往文献较少考虑退而不休与健康之间的内生性问题,本文采用倾向得分匹配方法在一定程度上解决了该问题。三是以往文献对老年人的健康度量比较单一,本文从自评健康、日常活动能力、抑郁情绪和认知功能四个方面度量健康水平,从而比较全面地考察了延迟退休政策的老年人健康的综合影响。
2 数据来源、研究方法和变量
2.1 数据来源
本文以北京大学“中国健康与养老追踪调查”(China Health and Retirement Longitudinal Study,CHARLS)项目调查数据为基础,该数据调查对象是随机抽取的45岁以上的人,旨在收集一套代表中国45岁及以上中老年人家庭及个人的高质量微观数据,用其来分析人口老龄化问题。2011年,该项目进行了全国基线调查,该调查包括全国150个县、区的450个村、居,并且成功访问了10257户家庭的17708个老年人,充分代表了中国的老年群体。由于农村地区劳动者从事农业生产活动以自雇形式较多,同时受雇者大部分也没有签订正式的劳动合同,退出劳动力市场不是出于制度的约束,“退而不休”行为难以界定,因此本文选取城镇地区户口类型为非农的60岁及以上老年人作为研究对象,经过整理和筛选,共得到1761个有效样本。
2.2 研究方法
老年人“退而不休”不是一个随机行为,而是其根据自身条件做出的选择,是自选择的结果,而且这些个体特征会同时影响劳动力供给和健康状况,所以很难区分究竟是退而不休影响了健康还是健康状况影响了退而不休行为的选择。在这种情况下,采用最小二乘法来估计会产生自选择导致的偏差问题。想要估计“退而不休”行为对健康的影响,最理想的办法是比较老年人退休后继续工作与不继续工作状态下的健康状况,这两种状态下健康状况的差别则是“退而不休”的健康效应。然而,现实中只能观测到每个老年人在一种状态下的情况。如果简单的用一位“退而不休”者和另一位“退而休”者之间的健康状况差异来估计,则会带来较大的偏差,因为两者在年龄、生活习惯等方面都可能存在区别,而这些区别会同时影响工作行为选择与健康。
为了解决该问题,本文利用倾向得分匹配(PSM)方法进行估计,该方法由Rosenbaum & Rubin(1983)最早提出[16],目前已成为处理非随机数据的重要实证方法之一。其核心思想是借助倾向得分构造反事实框架,将一个退而不休老年人和与其自身特征相似的一位退而休老年人进行匹配,由于两者在其他方面的各项特征相似,可以将匹配的“退而休”老年人的健康状况视为“退而不休”老年人退出劳动力市场状态下的情况,因此两组样本的健康差异可以归因于退而不休行为。
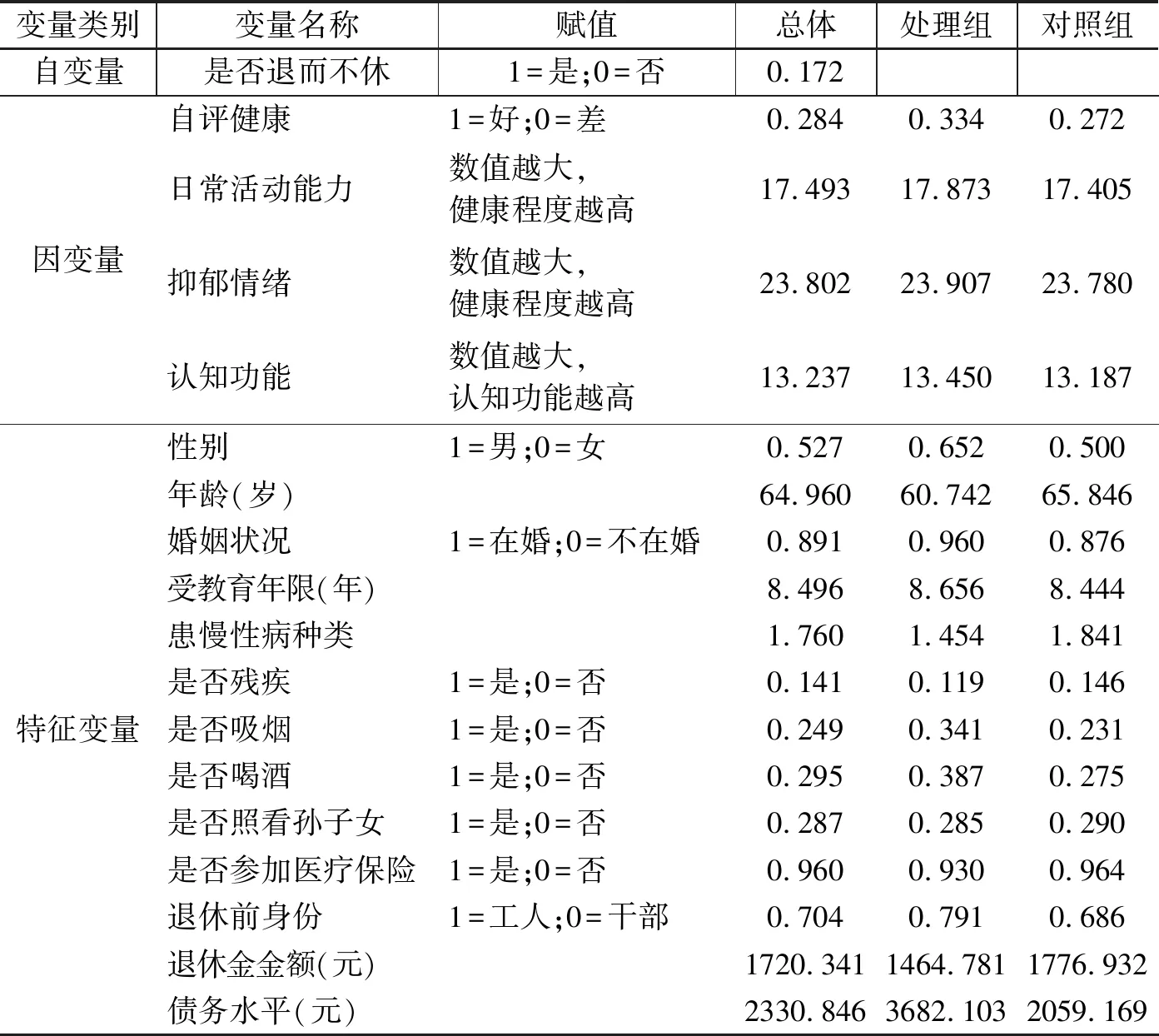
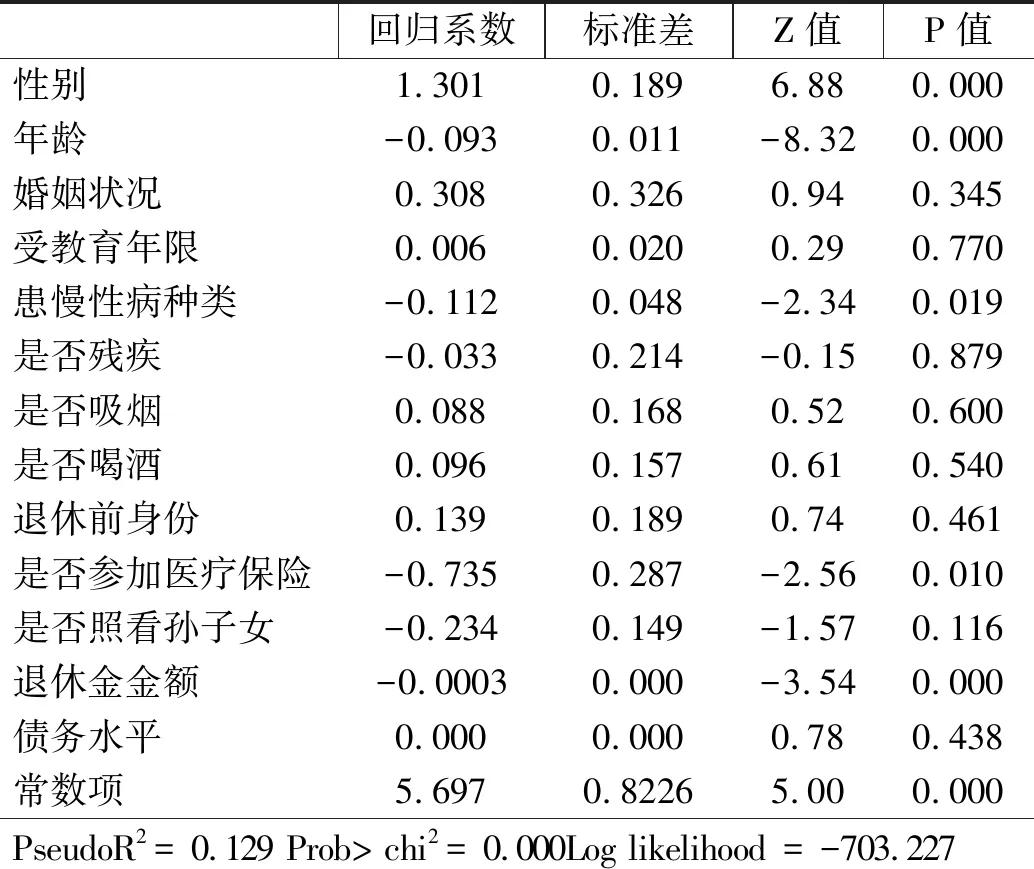
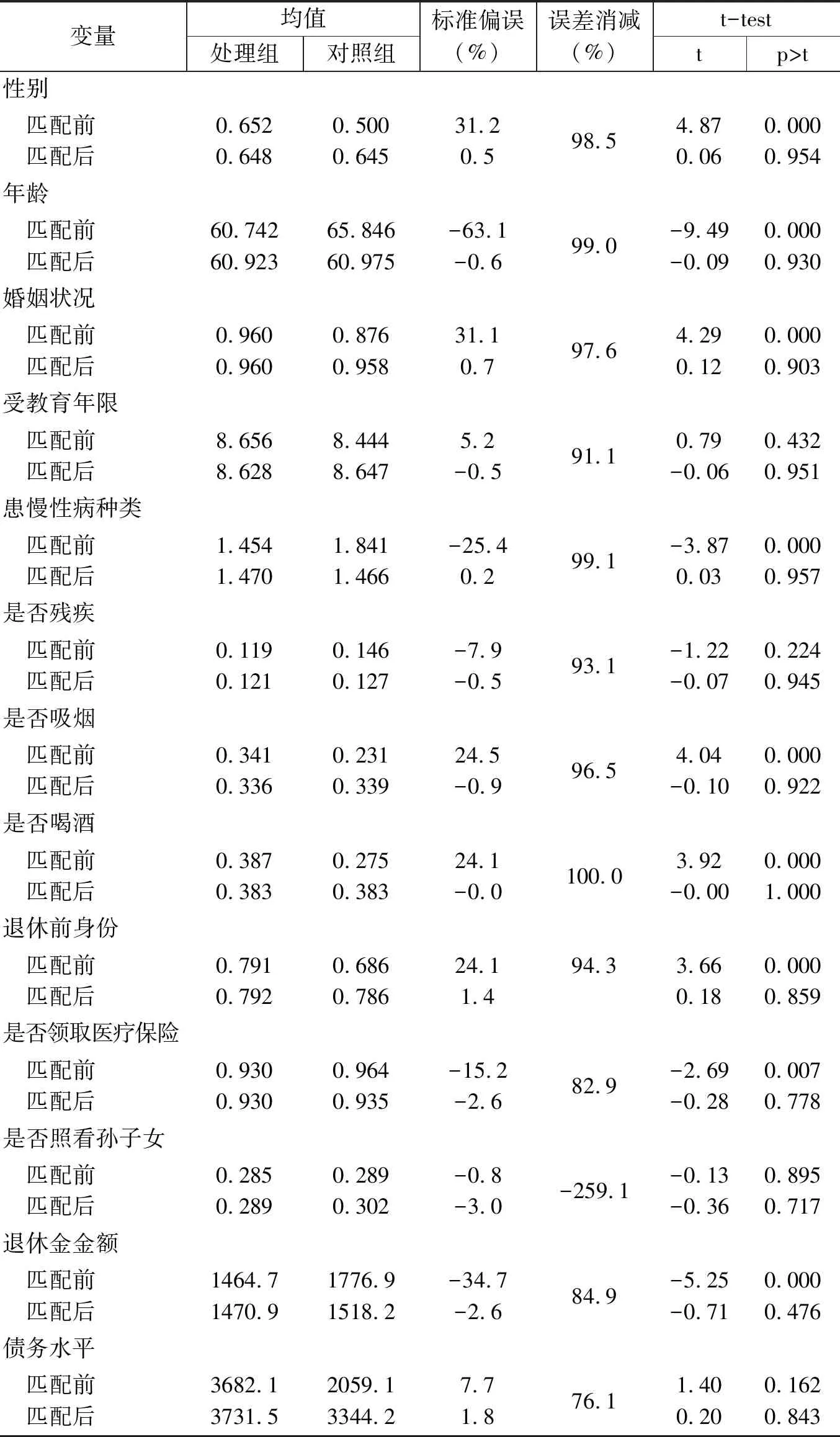
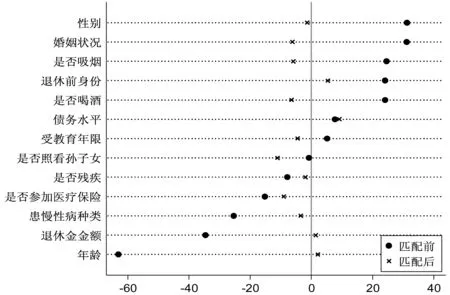
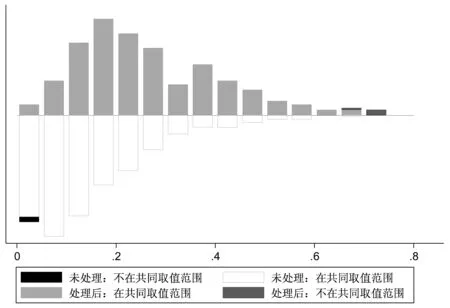
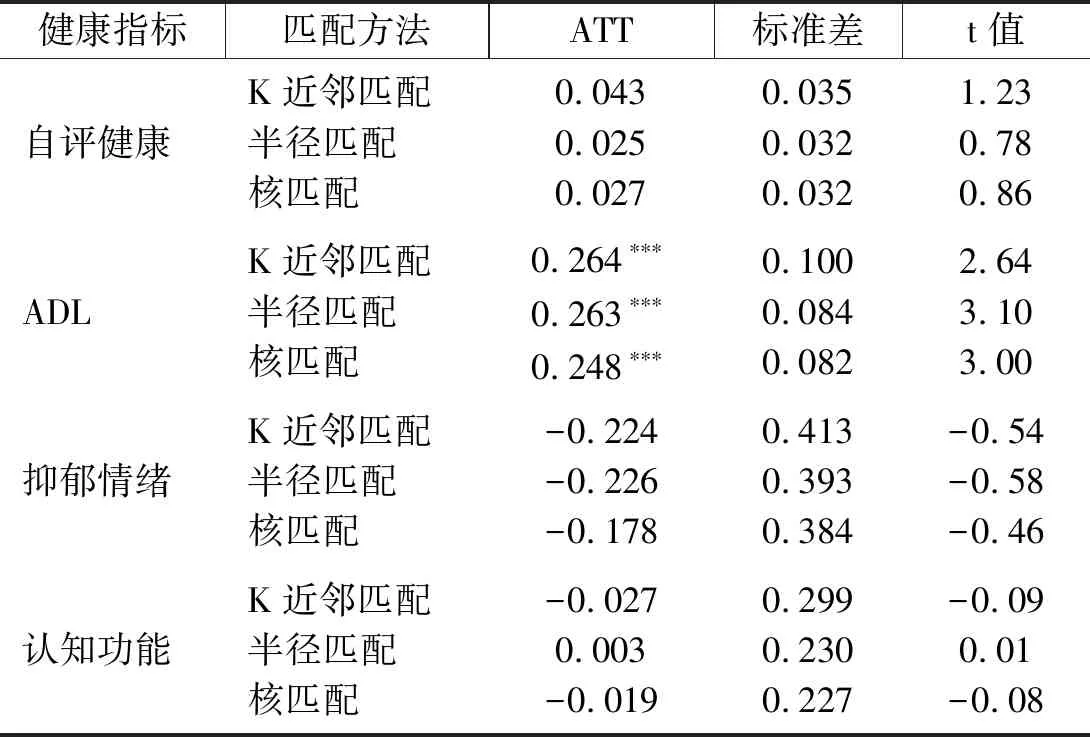
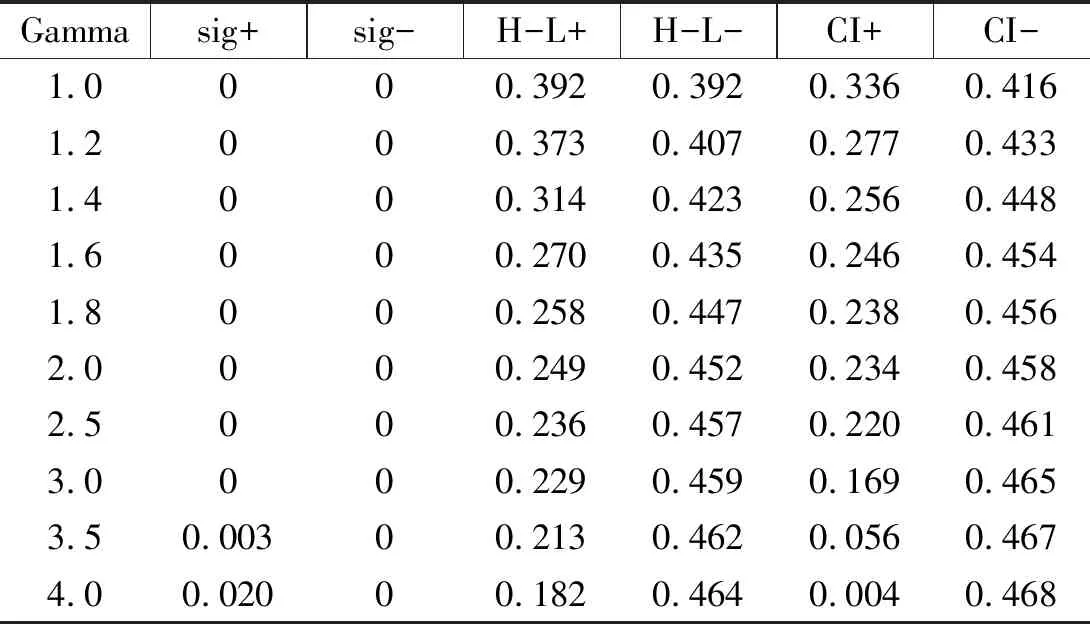
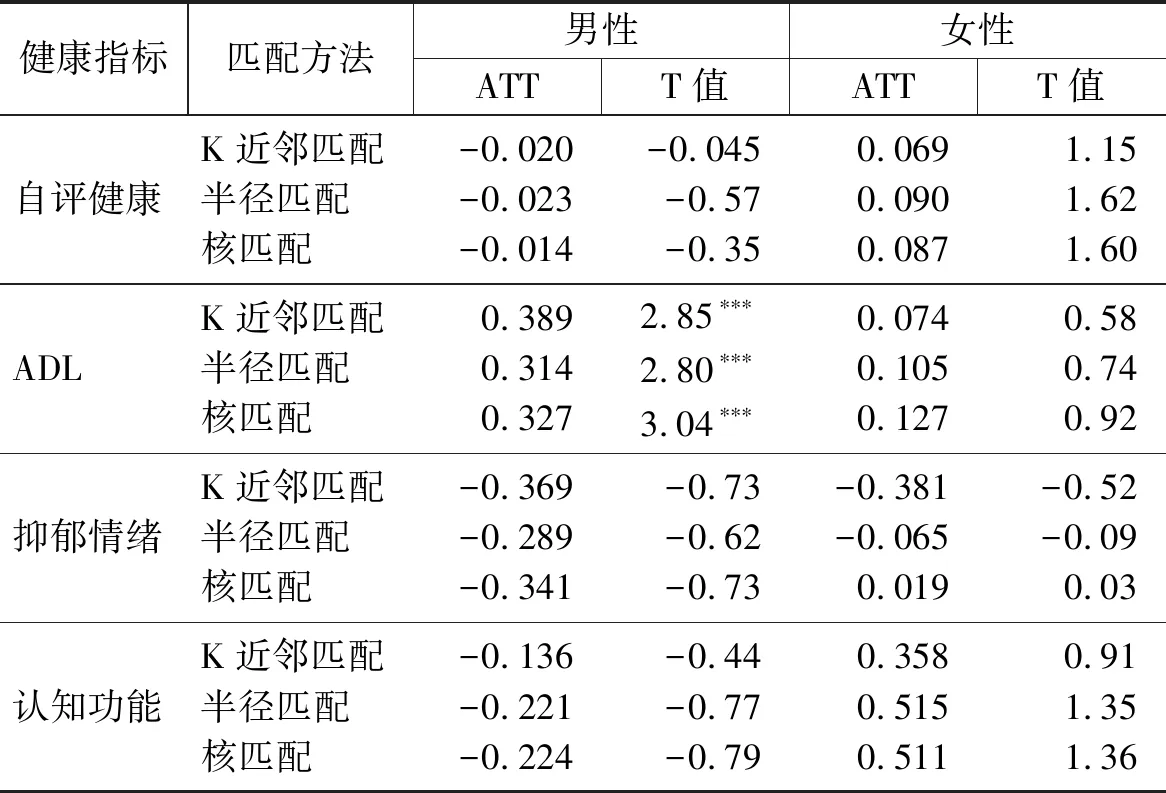
具体而言,我们设置虚拟变量Ti={0,1}表示退休老年人i是否还在工作,其中Ti=1表示“退而不休”老年人,为处理组;Ti=0表示“退而休”老年人,为对照组。本文将选取充足有效的匹配变量,并利用Logit模型对倾向得分进行估计,由该模型获得的样本接受处理的概率为倾向得分值,即p值,P=P(Ti=1)=μ(Xi)为退休者继续工作的概率,其中Xi为匹配变量。然后,我们采用倾向评分匹配法进行配对,PSM法将会根据处理组与对照组之间P值的相似度对二者进行匹配。这种配对方法的有效性取决于以下两个条件:条件独立性条件,即控制了共同影响因素后退休者健康水平的变化与其是否工作的决定是相互独立的,该假设要求尽可能多地观测到影响健康与工作的变量,由于本文的数据比较丰富,能够将同时影响两者的变量包含进来,未观测到的变量不足以产生系统性影响,因此该条件得到满足;共同支撑条件,即0 我们关心的是平均处理效应ATT,退而不休行为对老年人健康的平均处理效应可以由下式得到: ATT=E(Yi(1)-Yi(0)|Ti=1)=E{E[Yi(1)-Yi(0)|Ti=1,p(Xi)]} =Ep(Xi)|Ti=1{E[Yi(1)|Ti=1,p(Xi)]-E[Yi(0)|Ti=0,p(Xi)]} 其中,Yi(1)和Yi(0)分别为处理组和对照组退休者i的健康状况。 2.3.1 自变量:退而不休 即办理了退休和退职的老年人是否在劳动力市场中工作。具体而言,即询问退休人员在过去一年以及过去一周是否从事过报酬性工作,或者有工作但正在休假,如果回答为是,则说明其仍在提供劳动力供给,属于退而不休,赋值为1;如果为否,则赋值为0。 2.3.2 因变量:健康状况 健康包括多种维度,如身体、心理和社会适应性等。为了能够全面研究延迟退休政策对老年人健康的影响,我们选取了四个相关变量进行分析,包括自评健康、日常活动能力、认知功能和抑郁情绪。 (1)自评健康(SRH)。该指标基于问卷调查中的问题“您觉得自己的健康状况怎样”,答案分为六个选项,本文采用两分法对其进行分类:如果受访者回答“极好”、“很好”或“好”,则视为自评健康好,赋值为1;相反,如果受访者回答“一般”、“不好”或“很不好”,则视为自评健康较差,赋值为0。自评健康存在许多优良的特性,它不仅能够反映个人对自身身体与心理健康的主观评价与判断,同时也是预测死亡及严重或慢性疾病的重要变量[17],但该变量主观性较强,存在一定缺陷,如个体为了匹配其劳动状况谎报健康,造成识别性偏差等,因此,本文还将采取其他健康指标进行分析。 (2)日常活动能力(ADL)。包括穿衣、洗澡、进食、起床下床、上厕所、控制大小便六项基本活动能力,选项均为“没有困难、有困难但仍可以完成、有困难需要帮助、无法完成”,各个选项分别赋值为3、2、1、0分。六个问题所得分值相加为ADL分值,其中0分代表老年人生活完全不能自理,分值越高代表日常活动能力越强,身体越健康。 (3)认知功能(MMSE)。包括定向力、计算力、记忆力以及结构能力四个方面。定向力为询问老年人受访时的日期,包括年份、月、日以及星期、季节五个问题,每答对一题得1分,定向力为0~5分;计算力为采用问卷中的计算力度量,即100减去7等于多少?依次减去7,询问5次,每答对一题得1分,计算力取值为0~5分;记忆力为调查员读取10个词语后,受访者回忆并马上复述词语,几分钟后受访者再次复述词语,每答对一个得1分,取两次得分的均值,记忆力部分取值为0~10分;结构能力即在一张白纸上画有交叉的两个五边形,要求被测试者照样准确地画出来,正确则得1分。因此,认知功能指标赋值为0~21分,得分越高表示认知能力越强。 (4)抑郁情绪(D)。根据问卷中被访者对抑郁量表简表的回答得到。抑郁量表包含10个问题,其中8个为消极陈述,2个为积极陈述,选项均为“很少或根本没有、不太多、有时或者说有一半的时间、大多数的时间”,消极陈述各个选项分别赋值3、2、1、0分,积极陈述相反。从而抑郁情绪的得分为0~30分,得分越高表示抑郁程度越低,精神越健康。 表1 变量定义与描述性统计 2.3.3 匹配变量 本文将匹配变量分为三类:第一类为受访者个人特征变量,包括性别、年龄、受教育年限、婚姻状况;第二类为健康行为特征变量,包括患慢性病种类、是否残疾、是否吸烟、是否喝酒;第三类为社会特征变量,包括退休前身份、退休金金额、是否参加医疗保险、债务水平以及是否照看孙子女。 表1描述了匹配前样本的基本情况。在1761个有效样本中,退而不休者302个,退而休者1459个,处理组所占比例为17.1%。根据对因变量的分析可知,处理组在自评健康、ADL、认知功能、抑郁情绪四个健康指标上的均值都高于对照组,这在一定程度上说明退而不休者的健康水平优于退而休老年人,但不能说明两者之间存在因果关系,因为内生性存在,可能健康状况较好的老年人退休后更愿意继续工作。另外,处理组与对照组在各个特征变量上也存在明显的差异。具体而言,男性退休后工作的比例更高,处理组中男性所占比例为65.2%,而对照组这一比例仅为50%;退而不休老年人的年龄较低,均值为60.7岁,婚姻状况为在婚的比例较高;在健康特征与行为方面,处理组中患慢性病种类以及残疾比例均低于对照组,但是其吸烟、喝酒的比例较高;在社会特征方面,处理组退休前身份为工人的比例为79.1%,显著高于对照组的68.6%,另外,退而不休者的退休金金额低于对照组,而债务水平明显高于对照组。 表2 老年人退而不休的Logit模型估计结果 老年人退休后的工作决定取决于多种因素,倾向得分是给定这些条件的情况下接受干预的概率。本文将构造一个老年人退而不休参与概率的Logit模型,估计倾向得分,以完成处理组和对照组的匹配,该模型为: Logit(Ti=1)=β0+β1Xi+εi 其中,Xi为可能影响老年人退而不休概率的匹配变量。 表3 特征变量匹配平衡性检验结果 表2给出了老年人退而不休的估计结果。模型的Pseu-doR2值为0.129,说明模型的拟合优度较好。性别、年龄、患慢性病种类、退休金金额以及是否参加医疗保险变量对退而不休都有显著的影响,男性、年龄小、患慢性病种类较少、没有参加医疗保险、退休金水平较低以及债务水平较高的退休老年人更倾向于继续工作,而其他因素的影响则不显著。 倾向得分匹配估计的可靠性取决于“条件独立性条件”是否被满足,在获得老年人退而不休的预测概率后,接下来需要检验匹配变量和倾向得分在处理组和对照组之间是否存在显著差异,即平衡性检验。匹配后各个特征变量的标准偏差越小,说明匹配的效果越好,如果标准偏差较大,则说明匹配变量或匹配方法选取不当,倾向评分匹配估计无效。但对于标准偏差值的界定,目前没有统一的标准,因此,我们依据Rosenbaum & Rubin(1985)的标准,如果匹配变量的标准偏差值绝对值大于20时可认为匹配效果不好[18]。此处以Kernel匹配法为例说明样本的匹配效果,如表3所示。 根据表3最后一列t检验的相伴概率值可知,配对后处理组与对照组在性别、年龄、婚姻状况、受教育年限、患慢性病种类、是否残疾、是否吸烟、是否喝酒、退休前身份、退休金金额、是否参加医疗保险、债务水平以及是否照看孙子女方面均不存在明显的差异,且误差偏误的绝对值全部控制在20%以内,说明匹配效果较好,可以认为本文匹配变量选取恰当。另外,K近邻匹配法与半径匹配法的检验结果也与Kernel匹配法类似,不再赘述。 图1 各变量的标准化偏差图示 图2 倾向得分的共同取值范围 共同支撑假定是进行匹配的前提,该假定要求处理组与对照组的倾向得分取值范围有相同的部分。如果处理组都获得较高的倾向得分,而对照组都获得较低的倾向得分,则共同取值范围较小,匹配质量较差,因此需要进行共同支撑检验,以确保两组的倾向得分有足够多的共同区域[19]。图1与图2分别表示在Kernel匹配方法下协变量的标准化偏差变化和倾向得分的共同取值范围。由图1可知,匹配后变量的标准化偏差缩小,由图2可以直观的看出,大多数观测值都在共同取值范围内,因此在进行倾向得分匹配时仅仅会损失少量样本。 为了提高匹配质量,通常仅保留倾向评分重叠部分的个体,具体来说,如果处理组某个体的倾向得分高于对照组倾向得分的最大值或低于控制组倾向得分的最小值,则去掉该处理组个体,这样做尽管会损失一定的样本,但会提高匹配的准确性,减少偏差。因此,我们在处理组中剔除了4个观测值,而在对照组中剔除了14个观测值,最终处理组与对照组的样本量分别为298与1445个。 本文将分别使用K近邻匹配、半径匹配以及核匹配方法对退而不休的健康平均处理效应进行估计。经验表明,不论采用哪种方法,结果都不应该相差太大。表4报告了平均处理效应的估计结果。 表4显示,与个体特征相似的退而休的老年人相比,退而不休行为对退而不休老年人的日常活动能力具有显著的正向促进作用,而对自评健康、抑郁情绪和认知能力没有统计显著的影响。以半径匹配结果为例,在控制了选择偏差后,退而不休本身能够使老年人的日常活动能力得分提高0.263,且在1%的水平上显著,说明退而不休行为能够使老年人的生活处在较高的活动频率当中,而退而休的老年人由于活动较少,身体机能下降,从而其日常活动能力和身体健康水平明显低于退而不休者。 另外,退休会使老年人的生活状态、人际交往、社会地位等方面发生变化,一些老年人无法适应这些变化,心理健康水平会下降,而退而不休行为会阻止该进程,但根据本文的估计结果来看,我国城镇地区退而不休老年人的心理健康水平与认知功能并没有因为继续工作发生明显变化,我们认为,在目前阶段,我国退休老年人中由于兴趣以及对工作的热爱等因素而退而不休的所占比例较少,更多的退而不休老年人是出于经济原因继续留在劳动力市场,即城镇地区老年人退休后虽然有退休金,但部分老年人退休金水平较低,甚至债务水平较高,退而不休行为是外在因素所致,在这样的动机下,退而不休行为对其心理健康的影响较小。 表4 退而不休对老年人健康影响的平均处理效应估计结果 健康指标匹配方法ATT标准差t值自评健康K近邻匹配半径匹配核匹配0.0430.0250.0270.0350.0320.0321.230.780.86ADLK近邻匹配半径匹配核匹配0.264∗∗∗0.263∗∗∗0.248∗∗∗0.1000.0840.0822.643.103.00抑郁情绪K近邻匹配半径匹配核匹配-0.224-0.226-0.1780.4130.3930.384-0.54-0.58-0.46认知功能K近邻匹配半径匹配核匹配-0.0270.003-0.0190.2990.2300.227-0.090.01-0.08 本文通过倾向得分匹配方法控制选择性偏差,Rosenbaum将选择性偏差分为显在偏差和隐藏偏差,倾向评分匹配方法(PSM)只能根据可观测到的协变量进行调整,而未观测到的变量所导致的隐藏偏差仍然是个问题[20]。因此,为了考察所估计的平均处理效应的可信度,还需要进行敏感性检验,本文利用Rosenbaum边界方法进行检验。Gamma值为1表示老年人退休后是否工作的概率是一样的,通过赋予Gamma不同的值,Rosenbaum边界估计给出了老年人退而不休的显著性水平的上限和下限、Hodges-Lehmann点估计的最大值和最小值以及Hodges-Lehmann区间估计的上限和下限(95%置信区间)。如果Gamma的微小变动能够导致统计推论与假定研究不会有隐藏偏差情况下的统计推论极为不同,那么该研究就是敏感的;如果需要很大的Gamma值(通常接近2)才改变统计推论,那么该研究就是不敏感的。 表5 PSM估计的敏感性分析 表5给出了退而不休对日常活动能力的Rosenbaum边界估计。可以看出,在1~4的区间内,Gamma系数均没有体现出其敏感性,说明PSM估计的隐藏偏差可以忽略。此外,基于三种匹配方法的估计值差异不大,自评健康、抑郁情绪和认知能力的检验结果与日常活动能力结果类似,这说明上述使用倾向得分匹配方法估计退而不休行为对健康影响的平均处理效应结果是稳健的。 前文研究结论基于全体老年人的基础上,本部分则从性别和年龄两个方面进行进一步的经验分析。 3.6.1 性别差异 由于退休年龄、家庭角色等不同,男性与女性老年人的退而不休的选择行为及其对各自健康的影响也可能存在差别,因此本文分别对男女老年人退而不休的健康效应进行了估计。样本中男性为918人,处理组为193人,占21%;女性为825人,处理组为105人,占12.7%。估计结果如表6所示。 表6 分性别估计的平均处理效应 表6显示,男性和女性老年人退而不休行为对自评健康、抑郁情绪和认知功能均没有显著的影响,这与总体分析的结果相同。在日常活动能力方面,男性和女性老年人有不同的效应,即退而不休仅仅对男性老年人的日常活动能力产生了显著的正向促进作用,女性则并不显著。我们认为该现象的形成可能有两方面的原因:第一,退休前,女性的工作强度等方面一般都低于男性,退休后生活习惯、日常活动量等变化较小,工作与否对其日常活动能力的影响也小于男性;第二,我国女性在退休后,往往比男性承担着更多的家庭责任,包括日常做饭、家务、甚至照看孙子女等,这些活动在一定程度上与退而不休起到了相同的作用,能够使女性保持充足的活动量。 3.6.2 年龄差异 目前,世界上大多数发达国家退休年龄都已提高到65岁,在老龄化日益严重的背景下,许多学者建议我国的退休年龄也推迟到65岁,该政策是大势所趋[21]。因此,我们以65岁为界,将样本分为两组,以分析退而不休行为对不同年龄组老年人健康的影响。其中,65岁以上老年人的样本量为761,处理组为75人;65岁及以下老年人的样本量为982,处理组为223人。 表7的估计结果显示,退而不休行为对两组老年人的健康影响有较大差异。退而不休对65岁及以下老年人的自评健康和日常活动能力有显著的正向促进作用,而对抑郁情绪和认知功能没有统计显著的影响,这说明退休不休不仅不会对低龄老年人的健康产生负面影响,反而在一定程度上提高了低龄老年人的健康水平。退而不休对65岁以上老年人的日常活动能力有显著的正影响,对自评健康和抑郁情绪没有显著的影响,这说明退而不休总体上不会对高龄老年人健康产生不利影响,但是,值得注意的是,退而不休对高龄老年人的认知功能产生了显著的负向影响,政府在制定退休政策和劳动政策时,应高度重视高龄老年人的认知功能问题。 基于中国健康与养老追踪调查数据,本文利用倾向得分匹配方法估计了老年人退而不休对健康的影响,以此评估我国延迟退休政策可能产生的健康后果。研究结果发现,退而不休总体上并不会影响老年人健康水平,反而对老年人的日常生活能力有显著的正向促进作用,但这种正向作用只体现在男性老年人。同时,退而不休在一定程度上显著提高了低龄老年人(65岁及以下)的健康水平;退而不休总体上对高龄老年人(65岁以上)的健康没有影响,对日常活动能力有显著正向促进作用,但对认知能力有显著负向影响。 健康水平是延迟退休政策制定和实施的重要基础,劳动者担心延迟退休会损害自己的健康,我们研究结论在一定程度上为延迟退休政策的健康后果提供了证据。延迟退休政策不仅能在我国老龄化日益严重、新增劳动力供给逐渐减少和养老金压力增大背景下提高劳动力资源利用程度,促进经济发展,也能促进老年人健康水平,促进健康老龄化目标的实现。本文研究结论有以下四点政策含义:第一,基于目前老年人的健康水平,逐步把我国退休年龄提高到65岁的延迟退休政策,从健康角度看是可行的。第二,退而不休对低龄、男性老年人健康有正向影响,而对女性老年人影响不显著,考虑到我国女性老年人退休普遍较早,政府和企业要进一步改善女性老年人的就业和工作环境,这既有利于未来适当延长女性老年人的退休年龄,也可以保持和提高女性老年人继续工作时的健康水平。第三,维护老年人工作权益,提高老年人就业质量,减少因侵害老年人工作权益、就业质量低下给在职老年人带来的健康损害。第四,在实施延迟退休政策中可以采取灵活的退休年龄政策,对于健康水平低的劳动者可以选择较早退休,同时,政府和企业对继续就业的高龄老年人给予高度关注更有必要。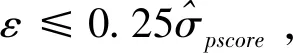
2.3 变量选取与描述
3 模型估计与分析
3.1 倾向得分估计
3.2 样本匹配平衡性检验
3.3 共同支撑检验
3.4 估计平均处理效应
3.5 敏感性分析
3.6 进一步的讨论
4 结论
