“人口红利”与“储蓄之谜”
——基于省级面板数据的实证分析
2019-04-12王树吕昭河
王树,吕昭河
(云南大学 发展研究院,云南 昆明 650091)
1 问题的缘起
改革开放至今已有40多年,我国经济在体量与质量上均得到了飞速的发展,而“人口红利”则是推动我国经济高速增长及现代转型的重要动力之一。有学者将人口红利定义为:快速的人口转变过程中,死亡率下降提早于出生率下降而引发时滞效应,之后,由于出生率的快速下降,致使人口年龄结构呈现“中间大、两头小”的形态,从而使得劳动力人口占比在一定时期内维持较高的水平,进而对经济增长产生有利的“人口条件”(钟水印,2016)。就我国的情况而言,建国以来的“第三次生育高峰”与严格的生育控制政策,使我国诞生了这样的“人口条件”,也有学者将其称之为“人口机会窗口”[注]有学者认为我国“人口机会窗口”的启动时间为1990年(于学军,1990),而由“人口机会窗口”转变为“人口红利”需要的是经济制度条件与人口条件的共同作用。1978年我国实施改革开放政策以来,大力发展的劳动密集型产业与劳动力人口的增加相契合,我国逐渐成为世界制造业大国,并使经济得到强劲的增长,因此收获了第一次人口红利。从上述概念可知,第一次人口红利的实现离不开快速的人口转变,而宏观层面上人口结构的剧烈变化,必然会引发微观家庭居民的经济行为发生变化,进而影响储蓄率发生变化。其次,根据第二次人口红利的概念,由于寿命延长效应及老龄化的加深,居民会为过长的“老龄期”谋划,因而增加储蓄,由此提高了国家的资本存量和为经济增长提供了新的资本条件(Mason et al.,2006;Mason and Lee,2007)。由图1可知,我国少儿抚养比逐年下降,老年抚养比则逐年增加,总抚养比自2010年下降至最低点的35.6%后有所增加,预期寿命不断延长,从1960年的43.7岁增加到2016年的76.3岁。而由图2可知,自20世纪80年代以来,我国居民储蓄率与经济发展程度较为相近的金砖五国相比,一直处于非常高的位置。但是,根据世界银行的计算,2007年我国居民储蓄率到达39.35%的峰值之后开始逐年下降。由此形成了“人口红利”与“高储蓄”同趋势并行的现象。本文将二者间的内在联系进行了理论分析,并运用实证分析方法进行了检验。
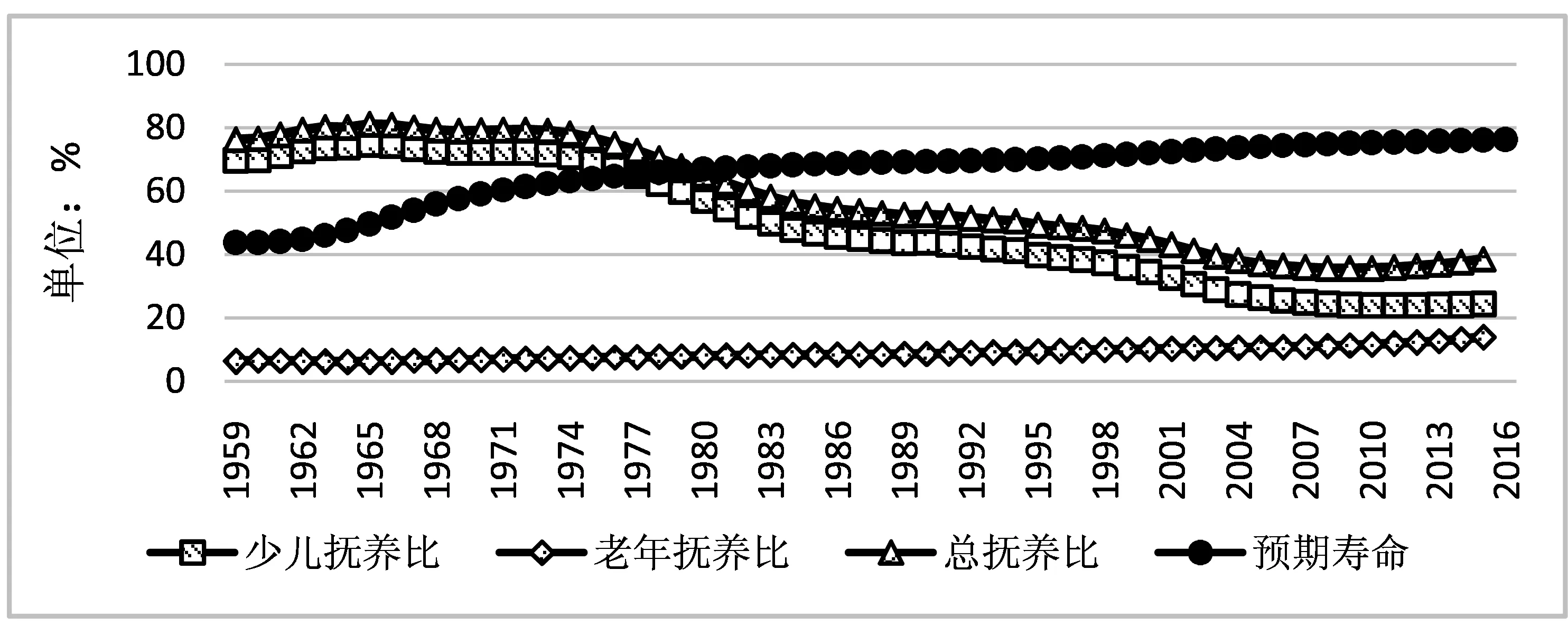
图1 中国居民预期寿命、总抚养比、少儿抚养比与老年抚养比(1959-2016) 数据来源:世界银行数据库
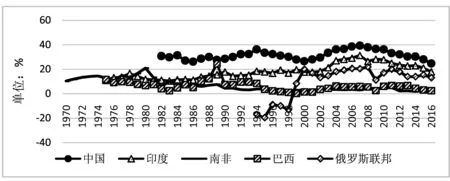
图2 金砖五国的居民储蓄率(1970-2016) 数据来源:世界银行数据库
2 国内外文献综述
2.1 国外文献综述
国外针对"人口红利"与"高储蓄"的相关研究寥寥无几,类似的研究主要集中在三条不同的主线上,一是研究预期寿命与居民储蓄的关系,二是老龄化与储蓄率之间的关系,三是人口结构对居民储蓄的影响研究。因此本文主要从以下三个方面进行阐述:
2.1.1 预期寿命与居民储蓄的关系
Ehrlich and Lui(1991)将寿命延长、生育和经济增长加入到OLG模型中,并将储蓄作为经济增长的一个表现形式,验证了寿命延长与储蓄之间存在正向效应。Futagami and Nakajima(2001)运用一般均衡模型得到了类似的结论。Bloom等(2003,2007)将健康和寿命延长效应加入到标准的生命周期模型当中,发现在寿命延长的预期会提升工作阶段的储蓄率,并用跨国面板数据进行了验证。Fukuda and Morozumi(2004)运用交叉代际模型通过跨国数据发现预期寿命增加可以提升居民储蓄。Park and Rhee(2005)通过韩国的微观数据发现抚养比的上升是储蓄率上升的主要原因之一,此外还有预期寿命以及消费习惯等同样可以解释储蓄过高的现象。Lee and Mason(2006)通过不同国家及地区的数据发现,预期寿命的增加提高了居民在老年阶段的风险性,由此增加了居民储蓄。而Braun等(2009),以及Kunze(2014)同样得到了类似的结论。
2.1.2 老龄化与居民储蓄的关系
部分学者发现老龄化会减少居民储蓄,Demery and Duck(2006)通过英国支出调查数据得到了这一结论。Horioka(2010)通过亚洲的数据运用时间序列的方法发现,持续的人口老龄化会带来居民储蓄率的下降。Yogo(2012)通过生命周期模型发现退休的老年人越多,他们面临着健康贬值的风险越大,因此会增加健康消费,从而减少了储蓄。Ongena and Zalewska(2017)发现机构很难通过保险的方式获得人们对健康的认同感,而老年人口比例的提高会增加这一群体的消费从而减少了储蓄。Grigoli(2018)通过多个国家的面板数据研究世界储蓄率的影响因素,发现人口老龄化的上升会导致储蓄率的下降。有部分学者发现老龄化可以增加储蓄。Hock and Weil(2006)通过连续世代交叠模型发现出生率下降引起的消费增加是短暂的,而老年人增加的预期会带来消费水平的下降以及储蓄率的上升。Curtis等(2015)通过OLG模型以及运用1963-2009年中国的数据发现老年人的增加意味着子女与父母进行更多的代际转移,总体来看增加了居民储蓄。
2.1.3 抚养比与居民储蓄相关研究
人口结构与居民储蓄的研究历史悠久,最早可以追溯到Modigliani and Brumberg(1954)的生命周期模型(Life Cycle Model),这一模型将居民的生命期间分为不同的阶段,研究表明抚养比越高储蓄率越低。Leff(1969)通过实证模型发现社会抚养比作为一种抚养负担,与居民的储蓄率呈现反向变动关系,这里与Modigliani and Brumberg(1954)的结论一致。Weil(1999)发现生育率减少的结果最终会使得劳动力减少,而在人均资本存量不变的假定下会使劳动力装备减少的投资转化为居民消费,从而使人均消费水平上升并且减少储蓄率。Doker等(2016)运用20个发展中国家1993~2013年的面板数据运用多个回归方程发现抚养系数与储蓄率的关系会随着城市化的变化而改变。而部分学者发现人口结构与居民储蓄率的关系不显著,Kraay(2000)运用中国的数据发现人口结构与居民储蓄没有显著关系。Wilson(2000)通过时间序列数据发现人口结构与储蓄水平关系不显著。Ramajo等(2006)通过OECD国家的面板数据运用工具变量法发现人口结构与储蓄率并没有显著关系。
2.2 国内文献综述
国内学者关注于人口红利相关因素与储蓄率的关系同样集中于三点:
2.2.1 预期寿命与储蓄之间的关系
贺菊煌(2003)在动态模型中将储蓄进行内生化,其研究发现寿命延长是导致储蓄的上升的重要因素,并认为如果可以将寿命的不确定性加入模型则更有意义。国内其他学者基于面板数据对二者进行了大量研究,多数研究通过面板数据得到类似的结论(郑长德,2007;范叙春、朱保华,2012;杨继军、张二震,2013;孟令国等,2013;张志远、张铭洪,2016;耿志祥、孙祁祥,2017;王颖、邓博文,2017)。金刚等(2015)将预期寿命分为工作与老年预期寿命,其中工作预期寿命与储蓄率呈负向关系,而老年预期寿命则相反,并且影响储蓄率的程度由二者共同决定。瞿凌云(2016)通过微观数据的数值模拟发现,在当前生育率水平下,预期寿命延长对养老储蓄率影响是非线性的,并呈现先上升后下降的趋势。
2.2.2 老龄化与储蓄之间的关系
多数基于面板数据的研究发现老龄化与储蓄之间具有促进作用(唐东波,2007;王森,2010;刘渝琳等,2014;李超、罗润东,2018),也有学者得到不一致的结论,汪伟、艾春荣(2015)通过将老龄化区分为负担效应与寿命效应,发现寿命延长的正效应会减弱负担效应的负效应,其变化存在正负转换的关系。另外,也有部分学者得到了老龄化对储蓄具有抑制作用的结论(陈彦斌等,2014;刘国斌、杜云昊,2015;钱先航、王可,2017;汪伟,2017)。
2.2.3 抚养比与储蓄之间的关系
在实证方面有大量研究表明少儿抚养比增加会导致储蓄下降(袁志刚、宋铮,2000;王德文等,2004;郑长德,2007;蒋云赟,2009;汪伟,2010;董丽霞、赵文哲,2011;徐升艳等,2013;刘渝琳等,2014;刘铠豪、刘渝琳,2015;孙涛、姜树广,2016;徐延明,2016);也有研究发现二者存在促进的作用(杨继军、张二震,2013)。大量研究表明老年负担比对储蓄率呈现正向影响(郑长德,2007;蒋云赟,2009;刘渝琳等,2014;刘铠豪、刘渝琳,2015),也有部分研究发现二者呈现负向关系(王德文等,2004;汪伟,2010;董丽霞、赵文哲,2010;杨继军、张二震,2013;孙涛、姜树广,2016);少数研究表明二者关系不显著,或呈现动态关系(董丽霞、赵文哲,2013;徐升艳等,2013;赵文哲、董丽霞,2013)。
2.3 国内外文献评述
上述文献主要基于人口结构和预期寿命的视角来研究居民储蓄,相比较而言,针对预期寿命与储蓄率的关系较为一致,近乎所有与预期寿命相关的文献皆表示其与储蓄率之间呈正向关系,即预期寿命的增加会提升居民的储蓄率。然而在人口抚养比与储蓄的研究领域则并无一致结果,多数研究从不同的视角来入手,其核心解释变量主要是少儿抚养比,老年抚养比,或者兼而有之。但相关的计量工具,研究方法及数据来源不同,致使研究的结论各异。因此,本文的创新之处在于:1.基于人口红利的理论视角来分析我国的居民储蓄率;将两次人口红利的人口特征全部运用于数理及实证模型中。2.在理论模型的分析上引入了预期寿命,且推导出人口结构、预期寿命对储蓄率的影响。3.运用动态的门槛模型研究了少儿抚养比和老年抚养比在不同的收入门槛内与储蓄间的趋势变化。
3 数理模型分析
3.1 家庭储蓄模型

代表性行为人在成年阶段的预算约束为:
(1)
代表性行为人在老年阶段的预算约束为:
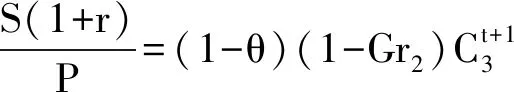
(2)
由此得到两阶段跨期的约束条件:
(3)
由于我国居民深受儒家文化影响,从抚养孩子和赡养老人的过程中可以得到效用,由此得到整体的效用函数为:
(4)
上式中,β表示时间的贴现因子;φ表示处于成年阶段的行为人从抚养孩子的过程中得到的贴现率;τ表示成年阶段的行为人从赡养老人的过程中得到的贴现率;大小皆在0到1之间。且效用函数采取对数形式。根据效用最大化原则以及给定的跨期约束条件得到均衡方程为:
C1= φC2
(5)
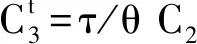
(6)
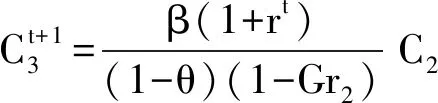
(7)
将(5)、(6)和(7)式代入(3)式可得:
(8)
将(8)式代入(7)式,再代入(2)式可得:
(9)
3.2 国家的储蓄模型
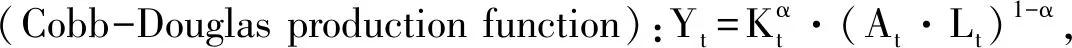
(10)
(11)
由(10)式可知:
(12)
根据(12)和(11)式可得:
(13)
将(12)式代入Cobb-Douglas 生产函数得:
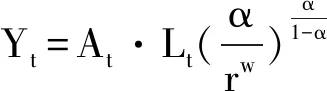
(14)
将(13)式代入(9)式,乘以当期的劳动人数,然后除以社会的总产出,由此得到社会的总储蓄为:
(15)
由(15)式对预期寿命求导,因为:
yd·φ+1+od·τ>0
(16)
所以:
(17)
容易得:
(18)
(19)
根据数理模型的推导,本文给定了需要检验的三个假说:
假说一:在上述的假设条件下,居民的预期寿命如果增加,由于要为了“过长的老年期”提前储蓄,导致居民的整体储蓄率上升,即预期寿命对储蓄率具有促进作用。
根据上述的假定,少儿、老年抚养比作为社会的纯消费群体,自身难以通过劳动获得收入,其数量的增加都会增加整个社会的消费,即会导致储蓄的减少,由此得到:
假说二:少儿抚养比对储蓄率具有抑制作用。
假说三:老年抚养比对储蓄率具有抑制作用。
4 实证分析
4.1 模型设定
本文主要基于两次人口红利的人口特征因素来分析我国高储蓄的现象,因此将少儿抚养比(Ydr)、老年抚养比(Odr)两个人口结构指标和人口预期寿命的替代指标:人口死亡率(Dr)作为核心解释变量。由于本文运用了各省份的数据,这些数据具有一定的内生性,主要包括居民的储蓄习惯,财政政策实施力度等,其来源于省份的个体特征,本文选用面板数据来消减这类内生性。模型分析上首先选用固定效应(Fe)和随机效应(Re)两种静态面板模型,其次选用动态面板模型,分别是DIFGMM方法和SYGMM方法。通常来讲SYSGMM是DIFGMM的优化模式,且在估计效率上也更高(ArellanoandBover,1995)。Blundell和Bond(1999)对这个模型进行了更加成熟的改善。因此,本文选用SGMM模型以获得更有效的工具变量从而进行更好的估计。SYS-GMM的水平和差分方程分别为:
水平方程:Yit=β1Yit-1+β2Xit+μi+εit
(20)
可以用的工具变量:D.Y[i,t-2][注]指Y的滞后两阶的差分。以作为Y[i,t-1]的工具变量
差分方程:D.Yit=β1D.Yit-1+β2D.Xit[注]通过水平方程取差分得到。+D.εit
(21)
可以用的工具变量:Y[i,t-3],Y[i,t-4]……
参考范叙春和朱保华(2012)的设定,为了防止扰动项的相关效应,因此需要加入Y的滞后三阶。(22)式中,μi代表地区固定差异项,εi表示随机扰动项。储蓄率计量公式为:
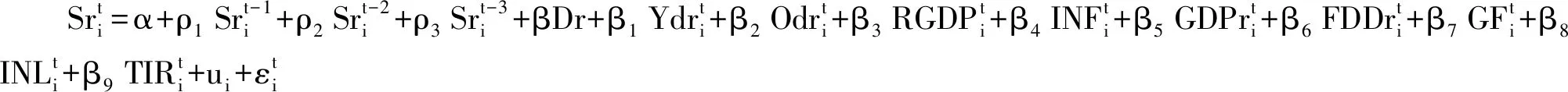
(22)
其中,Ydr、Odr分别表示少儿抚养比及老年抚养比;RGDP为人均实际GDP(支出法),代表了居民的人均可支配收入,并进行了CPI平减;INF表示通货膨胀率,用来体现物价变化对储蓄率的影响;GDPr为各省GDP(支出法)的增长率;FDD表示金融发展指数,这里以各省份金融机构年度贷款余额与支出法GDP的商来表示;公共财政支出比(GF)用政府公共财政支出占GDP的比例来表示;INL表示工业化率,用工业增加值除以支出法GDP;TIR表示产业高级化,即用我国第三产业就业人数占总就业人数的比例。
4.2 变量的计算依据和描述性统计
模型选用我国的29个[注]由于重庆市1997年前的数据缺失,而西藏部分数据缺失,因此将二者剔除。省市自治区1989~2015年共27年的省级面板数据进行分析。抚养比系数来自《中国统计年鉴》和《中国人口和就业统计年鉴》,其他变量来自《中国统计年鉴》以及《新中国六十年统计资料汇编》。具体的计算依据和描述如下:
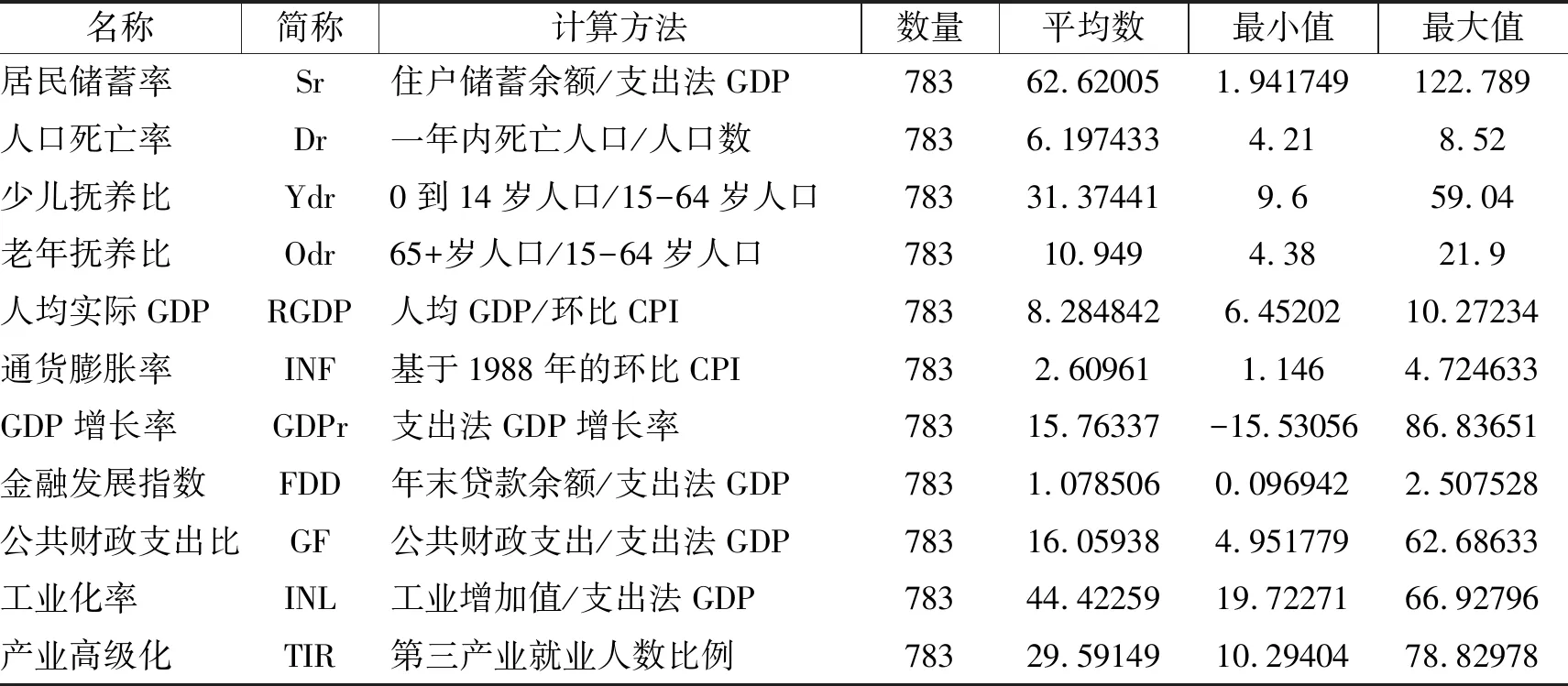
表1 各变量计算依据和统计性描述
4.3 初始计量
本文主要通过静态面板和动态面板两种方法进行初始的计量分析,从计量结果可以看到,无论是静态面板还是动态面板,Dr与Sr的回归系数非常显著,并且符号为负,由此证明了寿命的增加会带来储蓄率升高。Ydr与Sr同样具有显著的抑制作用,这里与本文的数理模型结论一致,根据我国实际情况,原因为:首先,生育控制导致Ydr不断下降,由于养育费用降低,储蓄动机则会变得更为明显;其次,由于生育数量的减少,导致家庭在养育孩子的行为上进行了“数量质量”替代,即为了孩子可以更好的发展,会对其教育资源进行投资从而提前储蓄(齐天翔,2000);最后,高房价及我国购买房屋的首付要求,父母为了孩子需要进行预防性储蓄。Odr对储蓄率具有促进作用,这里与数理模型有不一致的地方,但与很多现有的结论一致,首先,基于“二次人口红利”的理论,老龄化的加深和寿命的延长会让很多居民为了养老而增加储蓄。且我国法定退休年龄在多年内没有变化,很多居民在年轻时已经对养老时间延长存在着预期,这样会加强居民的预防性养老,因此会导致居民进行过度储蓄。其次,由于我国的社会保障制度有待完善,使得居民在退休后面临“养老”和“防病”等困扰,因此这一回归系数显著为正。最后,本模型数据的结构长度为27年,其中多数的老年人于我国40-50年代出生,这一代的老年人具有“勤俭节约”等优良品质,因此他们的消费减少而进行更多储蓄。
4.4 稳健性检验
模型采用三种方法来进行稳健性检验。参考郭峰(2015)、刘铠豪(2017)和戴翔、刘梦(2018)关于稳健性的检验方法,第一种,采取剔除异常值的方法,对核心变量进行缩尾,将储蓄率、人口死亡率、少儿抚养比和老年抚养比中5%以及95%分位数以外的数据进行剔除,并且将其数值替换为5%以及95%分位
数的数值。第二种,将作为核心解释变量的Ydr和Odr分别替换为少儿、老年与总人口数之比。第三种,采用一阶差分广义矩估计进行分析。经过上述检验由表3可知,各回归系数的符号不变,大小和显著性基本上没有变动。因此,本文运用静态、动态面板模型所得结论非常稳健。
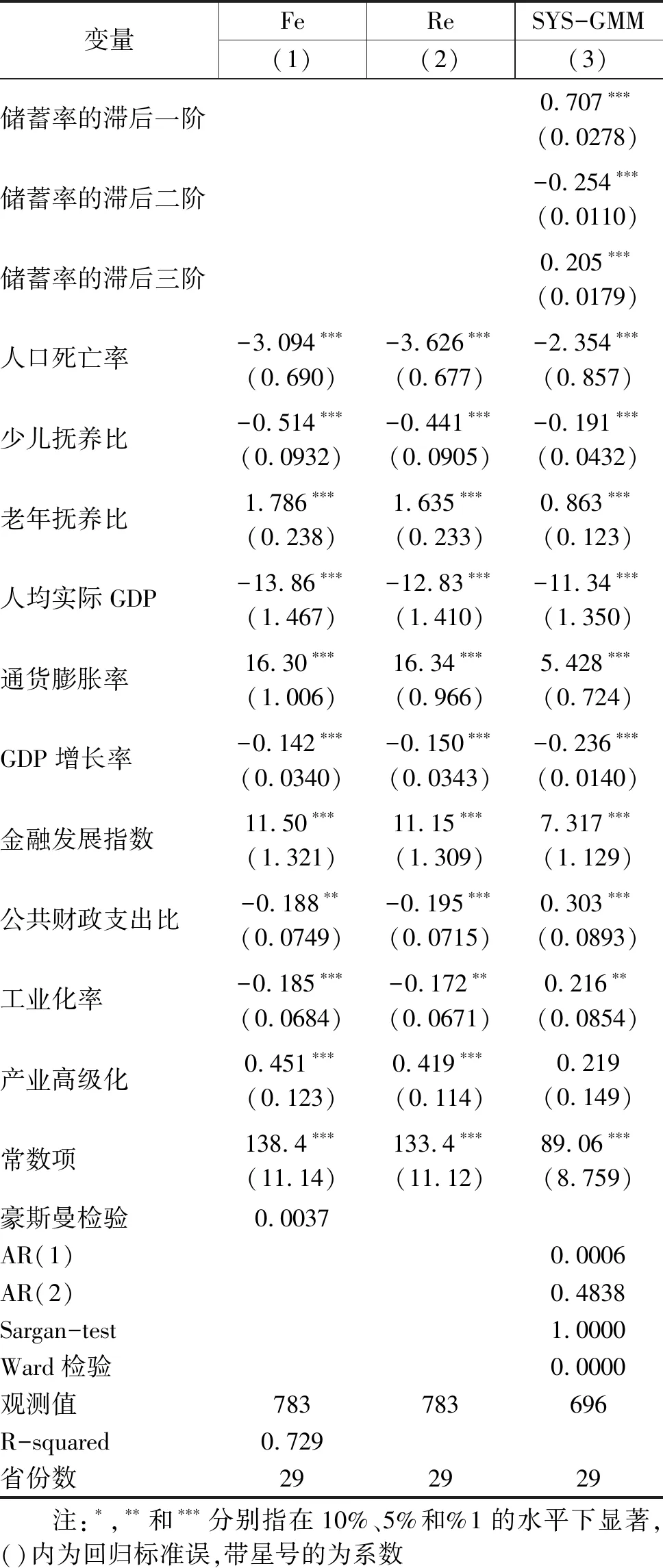
表2 初始回归结果

表3 稳健性检验
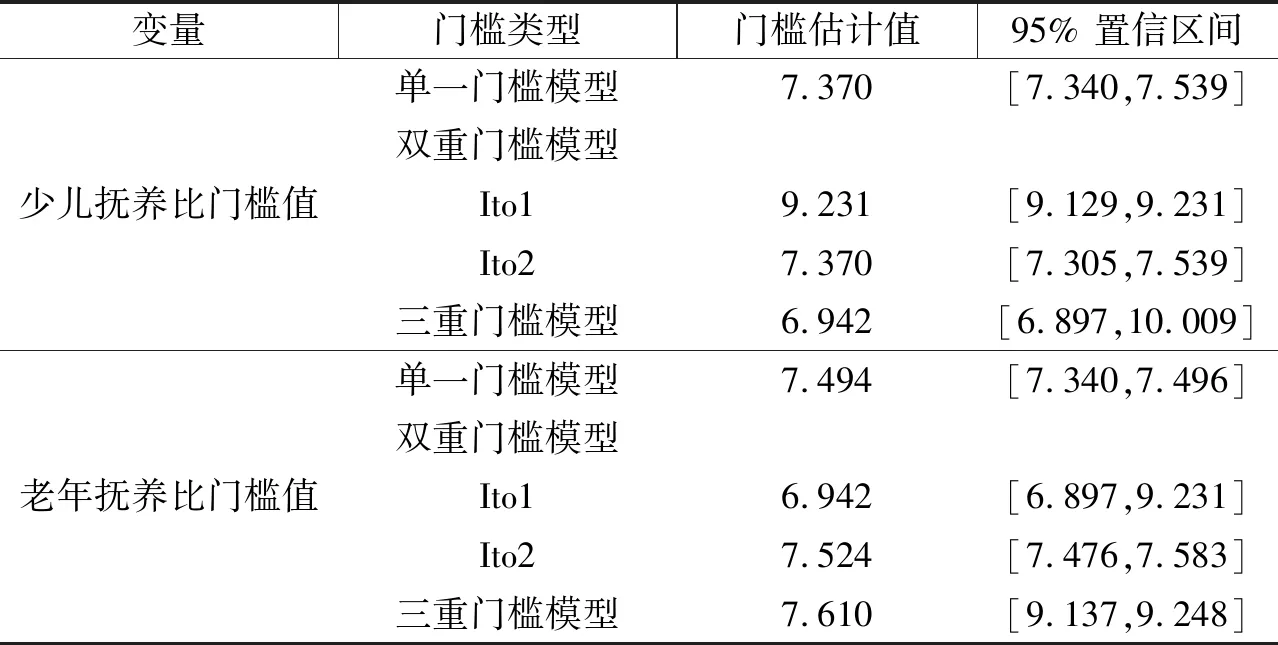
表4 门槛的估值与置信区间
4.5 面板门槛模型分析
从上面的结论可知,老年、少儿抚养比对储蓄率具有显著的影响,但储蓄的直接影响来源于收入,抚养比系数需要通过收入效应来影响储蓄,即人口结构与储蓄之间存在着结构突变效应,且这样的突变通常存在于人均收入的差异[注]这里引入一个假想国,如果一个国家的人口抚养比有一个较大的波动,但人均收入极低,由于根本没有多余的资金进行储蓄,储蓄率与人口结构并没有一个直接的联系,更没有内在联系。所以人口结构对储蓄的影响需要依赖于收入的变化。。前人的很多研究表明,关于Ydr与Odr对储蓄率回归系数的正负性颇有争议,有些学者将抚养比系数与人均收入进行交互分析,少数学者加入年份或省份等类别变量。此类方法可以减少伪回归的偏误,却也提高了其他的内生性,如省份分类偏误。基于上述原因,运用动态门槛模型给予深度分析。根据人均实际GDP即代表人均收入分为不同的区间来分析人口结构对储蓄的门槛影响。根据Hansen(1999)的门槛模型,采用Bootstrap方法确认门槛个数的显著性和数值。模型设定在区间内的数值个数最少为30[注]为了防止单个区间内的回归数值过少,从而产生伪回归的现象。,从而使抽样过程更合理。
其中,表4展示了门槛的估计值及置信区间,可以看到估计值都在置信区间当中,其确定门槛值的原理为Hansen(1999)的优化搜索方法,在搜索到第一个门槛值后,固定第一个门槛值,由此来搜寻第二个门槛值,然后再重新搜索第一个门槛值,直到门槛值较为稳定,由此得到比较准确的门槛值。且在表5中,展示了门槛个数的检验,总共进行了800次Bootstrap(自抽样法),由此极大地提升了估计的准确性。
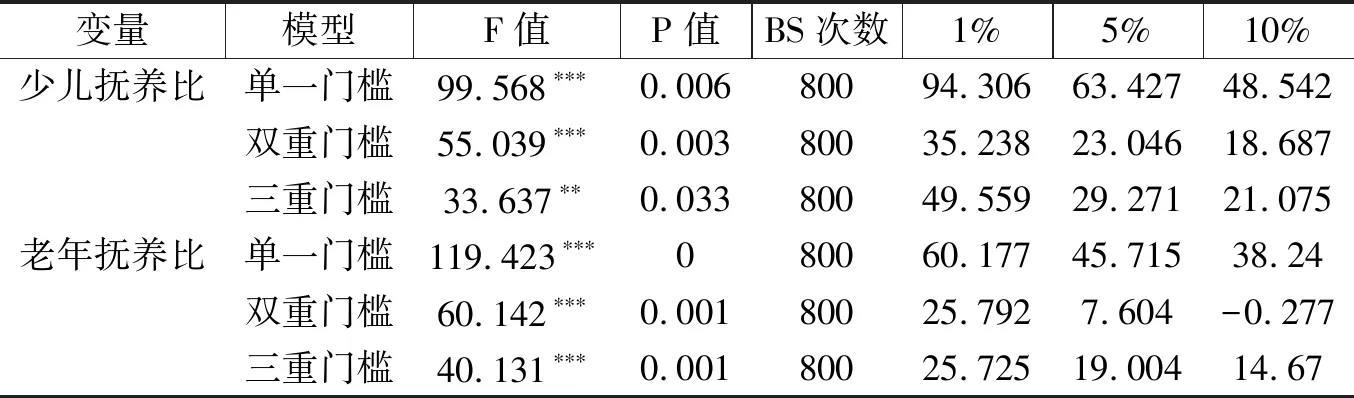
表5 门槛的个数检验
根据表5所示的结果可知,基于F统计量的显著性,以及门槛值的分析[注]如果两个门槛值过于接近,则证明这两个门槛值差异过小,因此本文会将其进行合并。,少儿抚养比的模型依据RGDP分为四个区间,分别为高收入群体(RGDP>9.231)、较高收入群体(7.37 首先,由(7)可知,在不同的人均收入的门槛里,Ydr对储蓄率具有不同的回归系数,且收入越高,系数的绝对值越小,即负效应越弱。由此可知我国居民收入越高,其中的抚养消费所占的比例则减少,表中可以看到Ydr对储蓄率的负向的作用逐渐变小,直到高收入群体中出现了系数不显著的现象。由(8)可知,不同的收入门槛内,Odr对储蓄率的回归系数同样发生了趋势性的变化,收入越高,正效应也越高。由此可知,人均收入的提升会使得居民对于老年的预防性储蓄效应增强。根据(7)和(8)来综合分析,收入处于低水平时,居民对孩子抚养的费用要占用大量的收入,从而使得居民的储蓄减少;且此时为了退休后的赡养储蓄动机不大。然而,当居民的收入水平不断提高,对孩子的抚养费用所占用收入的比例逐渐减少,居民会为了孩子进行教育投资,在居住和婚娶等方面进行预防性储蓄。从而使得Ydr对居民储蓄率回归系数绝对值越来越小;而老年抚养比对储蓄率的回归系数随着居民收入水平的不断提升则越来越大,收入的提升会使得年轻人为了保证老年的生活水平以及为预防疾病等而增加储蓄,且收入的提升会使得边际消费减少,而老龄化则进一步提高了储蓄的正向影响。因此,该结论符合我国的经济现实。模型的结论同样验证了我国地方省份收入差距过大,由此影响了居民储蓄行为的事实,如果收入差距缩小,社会抚养比(无论对老人还是少儿)的储蓄效应将会发生不同的变化,这样的过程不仅可以促进居民消费,并在人口红利逐步消失的背景下促进资本的良性运转,同时优化我国的经济结构,有效地保持我国经济增长所需要的“资本动力”,使我国经济可以得到高质量的发展。 表6 面板门槛的回归结果 本文研究我国人口红利与“高储蓄”两者并存的现象,发现“人口红利”与“高储蓄”具有内在必然关联性。首先,通过引入代际转移系数的OLG模型进行了数理分析,并通过实证模型进行了一定的检验,研究发现:居民预期寿命的延长会促进储蓄率的增加,少儿扶养比的提高则抑制了居民储蓄率增加,老年抚养比的增加促进了居民储蓄率的提升,结论十分稳健。之后,通过门槛模型的分析,收入越高,少儿抚养比的负效应越弱,老年抚养比的正效应越强。由此发现少儿、老年抚养比与居民储蓄率间呈现非线性的关系。因此,人口红利和“储蓄之谜”在演化趋势上存在内在关联性。 因此,随着我国第一次人口红利的消失和人口老龄化的加快,缩小我国居民的收入差距,可以为更加良性的国民储蓄行为提供条件,提前发挥二次人口红利的作用;其次,延长退休年龄可以促进居民的良性消费而减少过度储蓄;最后,尽快全面放开生育管制,既可以促进居民消费,也可以为我国未来的经济增长提供新的人口动力。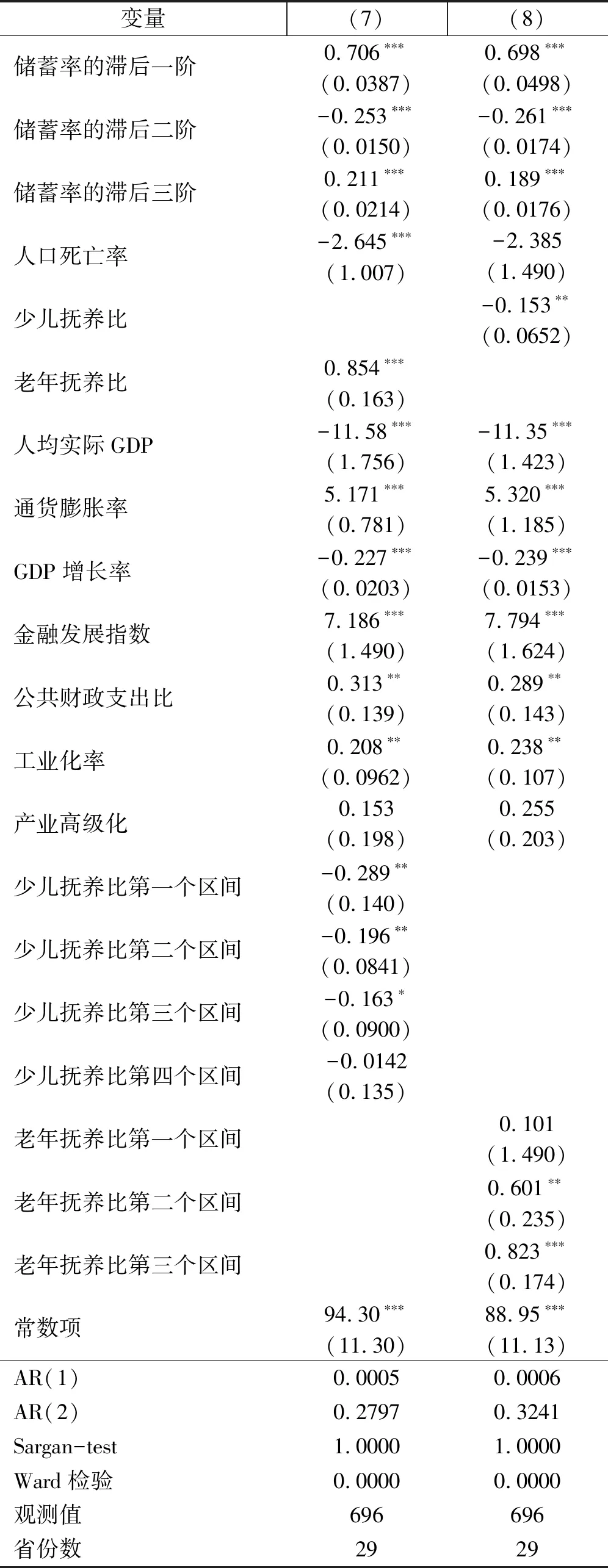
5 结论
