舰船水声信号特征提取方法研究
2019-04-11李环,李享
李 环,李 享
(沈阳理工大学 信息科学与工程学院,沈阳 110159)
海洋环境复杂、多样且时变性强,利用被动声呐检测到的水中舰船目标水声信号信息量少,甚至被环境噪声淹没。信号特征不仅可有效地表征信号信息,且可降低信号的识别维数,减少识别过程中的复杂度。
小波变换是处理时变信号的有利工具,其继承和发展了短时傅里叶变换的局部化思想,同时又克服了窗口大小不随频率变化的缺点。但小波变换存在仅对信号低频部分进行多尺度分解的局限性[1]。
本文提出利用具有良好正交特性的小波滤波器组构造小波库的方法,对信号进行分解,使得各频率段信号之间是正交的,不存在冗余。该方法可以克服小波变换的局限性,实现对高频信号进行多尺度分解,从而提取信号的波形特征值。
1 小波构造
1.1 构造原理
由小波的基本理论,可以得到满足理想重建条件的CQF(共轭正交滤波器组)基本方程[2]
P(z)+P(-z)=c
(1)
式中:c为常数;z为频域自变量;P(z)可表示为
P(z)=H0(z)H0(z-1)
(2)
式中H0(z)为分析低通滤波器。由H0(z)可得分析高通滤波器
H1(z)=z-NH0(-z-1)
(3)
式(3)的时域表达式为
h1(n)=-(-1)nh0(N-n)
式中:N为滤波器长度;n为阶次;h0为低通滤波器系数;h1为高通滤波器系数。

(4)
结合式(2)可得
(5)
根据式(3),由分析低通滤波器H0(z)可得分析高通滤波器H1(z),且H0(z)与H1(z)是正交的。
根据半带滤波器的特性[4],由半带滤波器可以得到满足CQF基本方程要求的P(z)。本文利用Kaiser窗函数设计半带滤波器F0(z),其冲击响应系数满足h(n)=h(-n),并且既满足可行性要求又有较好的频率特性。利用半带滤波器设计正交滤波器过程如下。
(1)根据设计目的,确定低通滤波器H0(z)的归一化通带截止频率ωp与阻带截止频率ωs及阻带最大衰减As,且ωp与ωs应满足ωp+ωs=π的设计要求。
(2)根据H0(z)的技术要求算出半带滤波器F0(z)的技术要求,半带滤波器的通带和阻带截止频率ωpf和ωsf,以及阻带最大衰减Asf。其中,半带滤波器F0(z)的最大衰减Asf与低通滤波器H0(z)的最大衰减As之间有如下关系
Asf=2As+20log10(2-10-As/40)
(6)
(3)选择用Kaiser窗设计FIR滤波器的方法[5]设计半带滤波器F0(z)。
(4)因式分解法求出正交低通滤波器H0(z)。
根据H0(z)可得到滤波器的单位冲击响应h0(n),通过对h0(n)做有限次数的迭代数值卷积运算[2],可得到小波尺度函数φ(t)。由分析低通滤波器与分析高通滤波器之间的关系可得到H1(z)与h1(n),同样对h1(n) 做有限次的跌代数值卷积运算,可以得到小波函数φ(t)。
1.2 正交滤波器设计及小波构造
根据目标信号的频率范围,设计低通滤波器的通带截止频率为ωp=0.37π、阻带截止频率为ωs=0.63π、As=40dB的分析低通滤波器。由式(6),可利用Kaiser窗设计通带截止频率为ωpf=0.37π、阻带截止频率为ωsf=0.63π、Asf=86.02dB 的半带滤波器F0(z)。
利用Matlab计算并仿真,可得到半带滤波器的单位脉冲响应图,如图1所示。

图1 半带滤波器单位脉冲响应
由图1可看出,单位脉冲响应满足h(n)=h(-n),且偶数项系数除常数项以外都为零,并且h(0)=0.5;奇数项系数按照滤波器设计要求得到,且F0(z)满足CQF基本方程。

滤波器系数h0=[-0.0014 -0.0072 -0.0137-0.0084 0.0072 0.0062 -0.0195 -0.0133 0.0883 0.2418 0.3125 0.2360 0.0992 0.0211 0.0164 0.0245 0.0149 0.0036 0.0012 -0.0005 -0.0039 -0.0036 -0.0003 0.0008 -0.0005 -0.0009 -0.0003 0.0000]
分析低通滤波器与分析高通滤波器的幅频特性曲线如图2所示。

图2 幅频特性曲线图
通过对h0(n)做迭代数值卷积[2],可得到小波尺度函数φ(t)。经过6次迭代数值卷积,并压缩为分析低通滤波器原来的长度,得到小波尺度函数的时域图和频谱图,如图3所示。
同理,通过对h1(n)做迭代数值卷积,可得到小波函数φ(t)。经过6次迭代数值卷积,并压缩为分析高通滤波器原来的长度,得到小波函数的时域图和频谱图,如图4所示。

图3 小波尺度函数的时域与频谱图

图4 小波函数的时域与频谱图
2 小波库构造
2.1 小波库构造原理
(7)

(8)
在同一尺度下得到的基本小波奇偶序数之间是正交的,即满足等式
(9)
2.2 小波库构造
水中舰船目标水声信号为低频信号,频率范围在0~30Hz内[1]。利用信号采集器采集信号时的采样频率为2048Hz。针对舰船目标信号的频率特征,并结合小波分解的一般理论,根据第8层的小波并结合式(7)构造小波库[2]。由8个第8层小波构成的小波库其基本小波如图5所示。

图5 小波库的基本小波
由文献[6]可知,由ω1(t)、ω2(t)、ω3(t)、ω4(t)、ω5(t)、ω6(t)、ω7(t)、ω8(t)基本小波分解可得到频率范围在0~4Hz 、4~8Hz、12~16Hz、8~12Hz、24~28Hz、28~32Hz、16~20Hz、20~24Hz内的信号。
3 信号特征提取与识别
3.1 信号特征提取
利用被动声呐采集模拟水中舰船水声信号,信号的时域与频域图如图6所示。

图6 目标信号时域与频域图
由图6b可知,信号频率在30Hz以内。利用构造的小波库中的基本小波ω2(t)、ω3(t)、ω4(t)和ω7(t)对15个目标信号样本及20个非目标信号样本进行分解,并用最小二乘法对35个样本进行训练,得到信号波形特征值,其中目标信号标签为A,非目标信号标签为B。根据训练结果,可提取频率范围在4~20Hz以内的信号波形特征值。信号经小波库中基本小波分解后,结合文献[7]中的最小二乘法训练,得到信号的波形特征值及特征维数如图7所示。
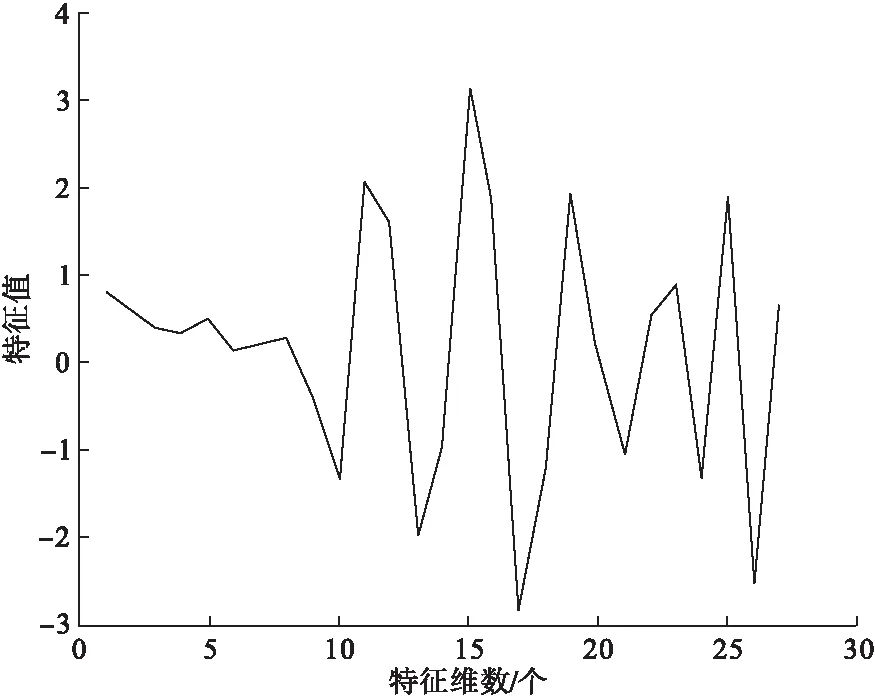
图7 训练特征波形结果
经小波库分解前,每个样本信号的长度为1660;分解与训练后,信号特征值长度为27,降低了信号识别维数。其中第1~7个特征值表征4~8Hz信号的特征波形,第8~20个特征值表征8~16Hz信号的特征波形,第21~27个特征值表征16~20Hz的信号特征波形。
3.2 信号识别
根据最小二乘法训练准则得到信号的特征值。将待识别的信号经小波库中同样的基本小波分解,分解结果与训练得到的特征值进行内积运算,若运算结果值为1,则该信号为目标信号;若运算结果值为-1,则该信号为非目标信号。
标签为A的样本信号,经分类器分类后仿真计算结果值为
1.0002 1.0000 0.9995 1.0001 0.9996
1.0011 1.0001 1.0015 1.0017 0.9988
1.0012 0.9969 1.0008 0.9972 1.0012
标签为B的信号样本,经分类器分类后仿真计算结果值为
-0.9999 -1.0011 -1.0006 -1.0000
-1.0003 -1.0005 -0.9980 -0.9997
-0.9995 -1.0011 -0.9992 -0.9964
-0.9973 -1.0016 -1.0018 -1.0036
-1.0000 -0.9976 -0.9988 -1.0037
由分类结果可知,分类结果误差在-0.005 ~ 0.005范围内,则当分类结果显示为0.995~1.005之间的值,则识别信号为目标信号;分类结果显示为-0.995~-1.005 之间的值,则识别信号为非目标信号。
将采集的舰船噪声水声信号与非舰船噪声水声信号利用小波库分解,经分类器分类后得到分类结果为
yA= 0.9988,yB=-0.9998
yA为目标信号,yB为非目标类信号,分类结果正确。以上结果表明,在分类结果误差允许范围内,建立舰船水声信号的小波库提取目标信号特征的方法,可实现对目标信号的识别。
4 结论
提出一种利用小波库提取信号特征的方法。该方法根据完全重构条件,构造具有舰船水声信号频率特性的小波,建立小波库;利用小波库中的基本小波对信号进行分解,并结合最小二乘法训练提取信号特征值。仿真分析和验证可知:利用该方法降低了信号维度,减少识别过程中的计算量,可以实现对目标信号的识别。
