城市环境下无人机TDOA定位中到达时间差误差统计模型

洪 伟 蔺诚毅 陈 婷

(西安电子工程研究所 西安 710100)

0 引言

城市环境下，由于缺乏统一的行业标准和规范，少数商用无人机处于“黑飞”状态，从而可能引发一系列安全事件。加强对无人机的管控已成为城市公共安全方面一项重要任务。

实现对无人机实时管控的前提是对无人机的精准定位，由于无人机与地面控制站之间具有无线通讯和控制链路，因此可使用电磁信号监测设备，通过处理无人机自身发出的电磁波信号(例如通讯信号)到达不同监测设备的时间差实现对无人机的定位。这种定位方法称之为时差定位(TDOA)。在二维平面内，无人机信号到达两监测设备的时间差确定了一对以两监测设备为焦点的双曲线，利用三个监测设备得到两组时差信息，得到两对双曲线，双曲线的交点即为无人机的位置[1]。

1 时差定位原理分析

如图1所示，T为无人机的位置，其坐标为(x,y)，A，B，C为三个监测设备的位置，其坐标分别为(x1,y1)，(x2,y2)，(x0,y0)。r0、r1、r2分别为目标到监测设备C、监测设备A和监测设备B的距离，距离差为Δri，i=1,2，则定位方程为：

(1)

其中i=1,2，c代表光速。

Δti表示信号到达时间(TOA)之差，即信号到达不同监测设备的时间之差。

对式(1)进行整理得到：

(x0-xi)x+(y0-yi)y=ki+r0Δri

(2)

将式2写成矩阵形式为：

AX=F

(3)

其中：

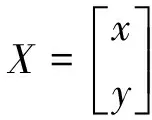
用伪逆法求得X的解为：

(4)

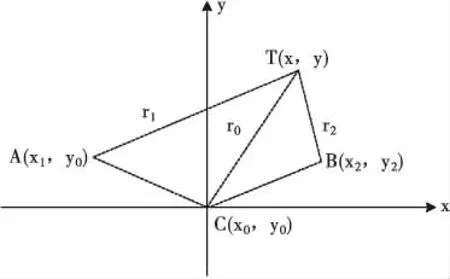
图1 时差定位原理示意图

令

(ATA)-1AT=[aij]2×2

(5)

则由式(4)得到目标位置的估计值为：

(6)

其中：

(7)

2 TDOA误差分析

2.1 无人机信号视距传播时的误差

当无人机信号监测设备周边无高大建筑、植被和地形遮挡时，可以认为电磁信号在无人机与监测设备之间沿直线传播，这种传播方式也称为视距传播。此时无人机信号从无人机到监测设备的传播时间取决于信号传播速度和无人机到监测设备的距离，并与距离呈线性关系，此时的误差来自信号检测。

2.2 无人机信号多径传播时的误差

城市环境下，由于各种障碍物的遮挡和地形的影响，无人机电磁信号只能以反射、折射和散射的形式传播，可以认为信号在无人机与监测设备之间存在多条直线传播，即多径传播。信号多径传播时，可以通过统计的方法研究特定环境下的传播误差，并分析其统计规律。

多径传播时，信号传播的时间比视距传播时间更长，即信号多径传播引起了附加时延τ。统计发现τ是一个服从指数分布的随机变量[2]，其概率密度函数为：

(8)

式(8)中的τrms是可以用式(9)表示：

τrms=Tdαβ

(9)

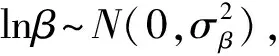
表1 环境与信道参数取值

信道参数T/μsασβ/dB繁华市区0.90.54一般市区0.40.54

假设从无人机到监测设备之间存在n条传播路径，n可以通过测量规律统计得到。监测设备能够检测到各支路信号，无人机信号视距传播时到达监测设备的时间为TOA0，时延最大支路信号到达监测设备的时间为TOAmax。同一监测设备检测到的各支路信号可看做是相互独立的，各支路信号的附加时延为τi，τi是一组彼此独立且都服从指数分布的随机变量，其概率密度函数可用式(10)表示：

(10)

其中τrmsi可由式(9)可知，具体表达式见式(11)和式(12)：

τrmsi=Tdαβi

(11)

(12)

故各支路信号到达监测设备的时间TOAi可表示为TOA0+τi，其中TOAi介于TOA0与TOAmax之间。TOAi越接近视距传播时间TOA0，监测设备检测信号到达时间引入的附加时延误差就越小。因此将各支路信号中最早到达监测设备的信号到达时间作为实际的信号到达时间，即实际的信号到达时间取值为TOA0+τmin。由于τi是一组相互独立且都服从指数分布的随机变量，其概率密度函数可由(10)可知，故τmin的概率密度函数为：

(13)

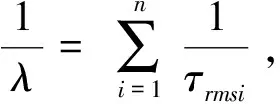
(14)

综上，城市环境下，多径效应使得监测设备检测到的无人机信号到达时间与视距传播下的无人机信号到达时间存在时间差τmin，τmin是一个服从指数分布的随机变量，其概率密度函数可由式(13)表示。

2.3 系统误差

监测设备在检测信号的过程中会带来时间误差，其大小取决于信号检测的手段和监测设备的精度，此时的误差称为系统误差。

系统误差是一个服从正态分布的随机变量，其均值为0，方差为一常量，由信号检测的手段和监测设备的精度决定。城市环境中各监测设备在检测无人机信号时引入的系统误差可看作是彼此相互独立的。

2.4 TDOA测量值误差的统计模型

假设利用m个监测设备对无人机进行TDOA定位，由于信道环境误差和系统误差的影响，第i个监测设备检测到的无人机信号TOA可表示为：TOAi=TOAi0+τi0+τimin，其中：

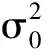
设第i个监测设备检测到的无人机信号到达时间为TOAi，第j个监测设备检测到的无人机信号到达时间为TOAj，则第i个监测设备和第j个监测设备检测到的无人机信号到达时间之差ΔTij为：

ΔTij=(TOAi0-TOAj0)+(τi0-τj0)+(τimin-τjmin)

(15)

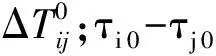
利用类正态分布[3-4]对服从指数分布的τimin和τjmin进行拟合，类正态分布的概率密度函数如下所示：

(16)

利用最小二乘法对两条概率密度曲线进行拟合，假设误差累计的平方和为Q，对于任意测量值ρ(τmin)，满足

(17)

由最小二乘意义下的最优拟合可令：

(18)

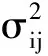
(19)

3 TDOA误差模拟实验

3.1 无人机信号TDOA误差统计模型的验证

模拟信号从无人机到监测设备1和监测设备2的传播情况。假设无人机信号到达监测设备1和监测设备2的多径数目均为10，可利用两种手段获得无人机信号到达监测设备1和监测设备2的到达时间差(TDOA)误差。

一种方法是通过信号到达时间差误差统计模型，随机产生一个误差作为模拟的TDOA误差。另一种方法是假设两个监测设备各自检测到的n条支路无人机信号中都含有因多径传播引入的附加延时τi，τi通过由式(10)随机产生，系统误差根据其正态分布的特征随机产生，将这两个误差叠加，最后通过求这两个监测设备获得的无人机信号到达时间之差获得的TDOA作为实际的TDOA误差。进行10000次模拟试验，统计得到模拟TDOA误差和实际TDOA误差的概率密度曲线，如图2所示。

图2 TDOA时延概率密度分布曲线

由图2可知，通过概率密度函数模拟的无人机信号TDOA误差与实际的无人机信号TDOA误差非常接近，因此该统计模型能反映出无人机信号到达各监测设备的到达时间差误差的统计规律。

4 结束语

本文给出了一种城市环境下无人机时差定位原理，并分析了无人机TDOA定位中TDOA测量值误差的主要来源，即多径传播引起的时延、监测设备检测信号引起的误差。从城市环境中无人机信号多径传播的附加时延的统计规律出发，分析建立了无人机信号到达各监测设备的TDOA误差统计模型。最后通过Matlab进行模拟试验，验证了TDOA误差统计模型的有效性，该模型反映了城市环境下无人机信号TDOA误差的统计规律，是进一步研究TDOA定位误差的基础。