参数化双频连续波模拟目标回波产生器的设计与实现

程超才 陆泽橼 贺 芃 朱子平

(中国电子科技集团公司第三十八研究所 合肥 230088)

0 引言

在雷达系统中，雷达波形的选择对系统探测性能的影响尤为关键。通常，情报雷达选用单脉冲，线性调频脉冲，相位编码脉冲等作为发射波形，以减小截获概率，但这种系统受雷达发射功率，发射波形时宽和带宽等因素的限制，测速和测距等精度通常不高。

单频连续波雷达在速度测量方面具有极大的优势，随着计算机技术，电子科学技术和信号处理等技术的发展，基于快速傅里叶变换的频谱计算方法能够实时估计被测信号的频率，并根据估计结果对非整数次谐波分量引入的附加相位进行补偿，从而估计出被测信号的相位[1-2]。但是，单频信号在测距方面存在严重的距离模糊，根据雷达的工作频段，其最大不模糊距离通常在cm量级，无法满足雷达系统的测距需求。

为了解算由单频测距引入的距离模糊，近年来提出了多频参差测距法，二次相差法等算法[3-5]。多频参差测距法通过同时或顺序发射几组符合一定参差关系的双频信号，通过解同余方程组得到目标的最大不模糊距离。二次相差法顺序发射几组双频信号，从而在满足测距精度的情况下，获取目标的最大不模糊距离。

现代雷达系统要求能够快速、实时捕获，跟踪和测量目标参数，为了衡量雷达的实时处理性能，同时在雷达整机尚未完备情况下为系统联调提供测试手段，在双频连续波雷达系统中需要实时产生能够模拟真实目标回波的模目信号。

1 目标运动模型

1.1 单频信号的模目特性

在单频连续波雷达系统中，雷达发射机向外辐射调制的单频信号，发射信号模型为：

xT(t)=cos(2πfct+φ0)

(1)

其中，fc为雷达工作频率，φ0为发射初相。

电磁波被目标反射后返回雷达接收机，接收回波信号的模型为：

xR(t)=σcos[2πfc(t-τ)+φ0]+xn(t)

(2)

其中，σ为目标散射截面积，τ为反射点处的双程延迟差，xn(t)为引入的加性高斯白噪声。

接收机接收的回波信号经放大，混频，滤波，检波，AD采样等处理后，得到两路正交的零中频数字信号，其复信号数学模型为：

xD(nTs)=σ1exp[j(-2πfcτ+φ1)]+xn(nTs)

(3)

其中，σ1为处理后回波信号的幅度，φ1为由电子线路延迟等引入的残余初相，n为非负整数，Ts为采样间隔。

考虑目标的机动性能，假设目标运动模型为匀加速运动模型，t时刻目标距离为R(t)，那么

(4)

式(4)中，R0为基准时刻目标相对雷达的初始距离，v0为目标的初速度，a为目标的加速度。

通常，在雷达的一个处理周期中，由于速度和加速器引起的速度变化远小于光速c，因此，反射点的双程延迟差[6]近似为

(5)

将公式(5)代入公式(3)，得到单频信号下模拟目标回波的表达式：

xD(nTs)=σ1exp[j(θR+θv+φ1)]+xn

(6)

1.2 双频信号的模目特性

双频连续波雷达发射机同时向外发射载频分别为f1和f2的射频信号，使用两部接收机同时接收目标回波，双频模目的表达式为：

(7)

由公式(7)可知，双频模目之间的相位差：

Δθ= (θR1-θR0)+(θv1-θv0)+(θa1-θa0)+
(φ11+φ10)

(8)

式(8)中，由速度和加速度项引入的相位差可以通过相关处理和FFT谱峰估计进行补偿，残余初相可以通过零距离标校的方法进行补偿[7]，因此距离的表达式为：

(9)

假设载波频差f1-f0=10kHz，光速c=3×108m/s由公式(9)可知，最大不模糊距离为R0=15km，由双频信号的一次相位差获得的最大不模糊距离远大于雷达的工作波长，通过参差重频法、二次相差法等方法可以进一步扩大雷达的测距范围。

2 双频模目产生器的工程实现

2.1 系统框图

双频模目需要根据系统要求产生受工作频率，回波信号幅度，目标速度，加速度，角度和距离等参数调制的双频连续波，并叠加一定信噪比的高斯白噪声，以满足系统目标检测和参数估计的要求。

双频模目产生器系统简化原理框图如图1所示。由嵌入式实时处理器产生系统控制字并送到时序产生模块，时序模块截取控制字内容，用于产生整机工作时序，并将模目参数送到模目产生器，其中工作时序通过射频电缆传输，模目参数通过光纤传输。

模目产生器选用数字信号处理器(Digital Signal Processor，DSP)+现场可编程逻辑门电路(Field Programmable Logic Gate Array，FPGA)的处理架构，DSP负责模目参数控制和计算，FPGA负责流水方式产生指定模目。DSP选用ADI公司的TS201，FPGA选用ALTERA公司的EP4SGX360NF45I3。FPGA收到控制字后，以中断方式通知TS201取走，TS201对参数进行处理，并在系统工作时序到来前将计算、量化后的模目参数通过总线方式写入FPGA，由FPGA产生两个频点的零中频数字信号，并送到其他分系统进行处理。

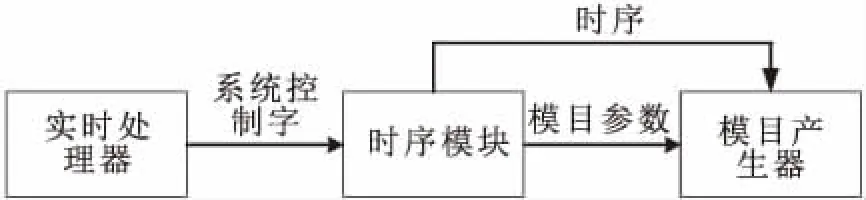
图1 双频模目产生器系统框图

2.2 实现方法

双频模目产生器主要在FPGA中实现，图2给出了双频模目产生器的原理框图。使用开发工具提供的数控振荡器(Numerically controlled oscillator，NCO)IP核，可以产生频率分辨率高，频率切换速度快以及相位连续的单频信号。

单频信号经过复数乘法运算，完成幅度加权，再与高斯白噪声相加完成加法运算，产生单个目标叠加高斯白噪声的模拟目标回波。采用参数化设计方式，可以实现工作在两个频点，包含两个甚至多个目标的模目信号，如图2所示。多个目标回波经过加法运算，抽取操作后将数据率降到系统给定的采样率，并按照一定顺序排列后送到信号处理分系统。

通过控制幅度加权，可以模拟不同目标回波的信号强度，目标回波的信噪比，以及产生和差波束模拟测角过程等。高斯白噪声采用查找表的方式实现，由FPGA提前存储一组均匀白噪声到内部存储器，再利用均匀分布与高斯分布之间的映射关系产生高精度高斯白噪声[8]。

图2 FPGA中产生双频模目原理框图

2.3 主要参数计算

由于单频连续波存在严重的相位模糊，由公式(7)可以得到由半波长的小数部分定义的模糊相位，该相位由目标的初始距离产生，即

(10)

式(10)中，mod表示求模运算，floor表示向下取整，λi=c/fi表示系统工作波长。

由离散化的一次相位可以得到相邻采样点的一次相位增量，即

(11)

式(11)中，Fs=1/Ts表示系统采样率。

由离散化的二次相位可以得到相邻采样点的二次相位增量，即

Δ2θai=[θai(n+1)-θai(n)]-

(12)

使用NCO时需要配置相位调制寄存器，相位增量寄存器和频率调制寄存器等参数，这些参数由半波长的小数部分对应的模糊相位，一次相位增量和二次相位增量经过量化得到。

因此，归一化的相位调制寄存器计算公式：

(13)

归一化的相位增量寄存器计算公式：

(14)

归一化的频率调制寄存器计算公式：

(15)

其中，round表示四舍五入取整，Nb1，Nb2，Nb3表示NCO内部各寄存器的量化位宽。

2.4 实现结果

假设双频模目产生器产生两个目标的模拟回波，工作频点分别为f1=10GHz和f2=10.000001GHz，频差Δf=1kHz，光速c=2.99792458×108m/s，因此最大不模糊距离Runamb=149.9km，两个目标的主要运动参数如表1所示。

表1 设计的目标运动参数

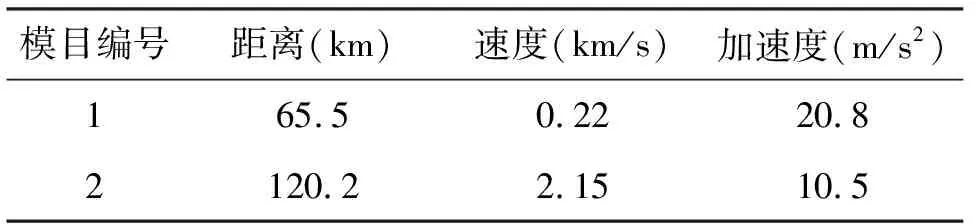
模目编号距离(km)速度(km/s)加速度(m/s2)165.50.2220.82120.22.1510.5

假设两个目标的回波信号强度相等，每个波束的驻留时间为100ms，处理时钟Fs=120M，按照96∶1进行抽取，抽取后的采样率Fsd=1.25M，这样每个驻留时间内的采样点数约为125000，NCO内部各寄存器的量化位宽分别为Nb1=32，Nb2=60，Nb3=60。

由表1中的模目运动参数可以得到NCO中各调制寄存器的计算结果，如表2所示。

表2 调制寄存器的计算结果

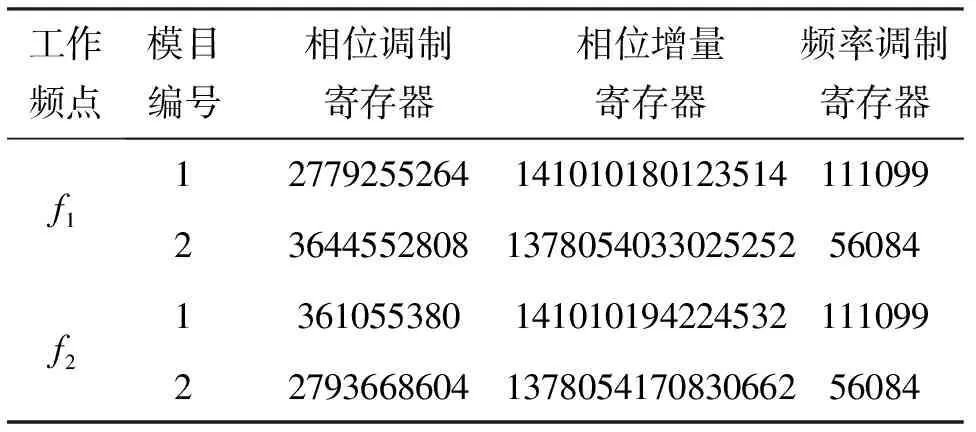
工作频点模目编号相位调制寄存器相位增量寄存器频率调制寄存器f11277925526414101018012351411109923644552808137805403302525256084f2136105538014101019422453211109922793668604137805417083066256084

对两个工作频点，分别绘制加噪声和不加噪声两种情况下模目信号的频谱，如图3、图4所示，频谱计算选用FFT点数为65536，每个频点下加噪声时模目1和模目2的信噪比均为-10dB。

图3为不加噪声时，工作频点f1和f2下双频模目的频谱。由于f1和f2接近，不同频点下同一目标的多普勒频率非常接近。同时，由于存在加速度产生的二次相位，FFT变换后的谱峰有一定的展宽。

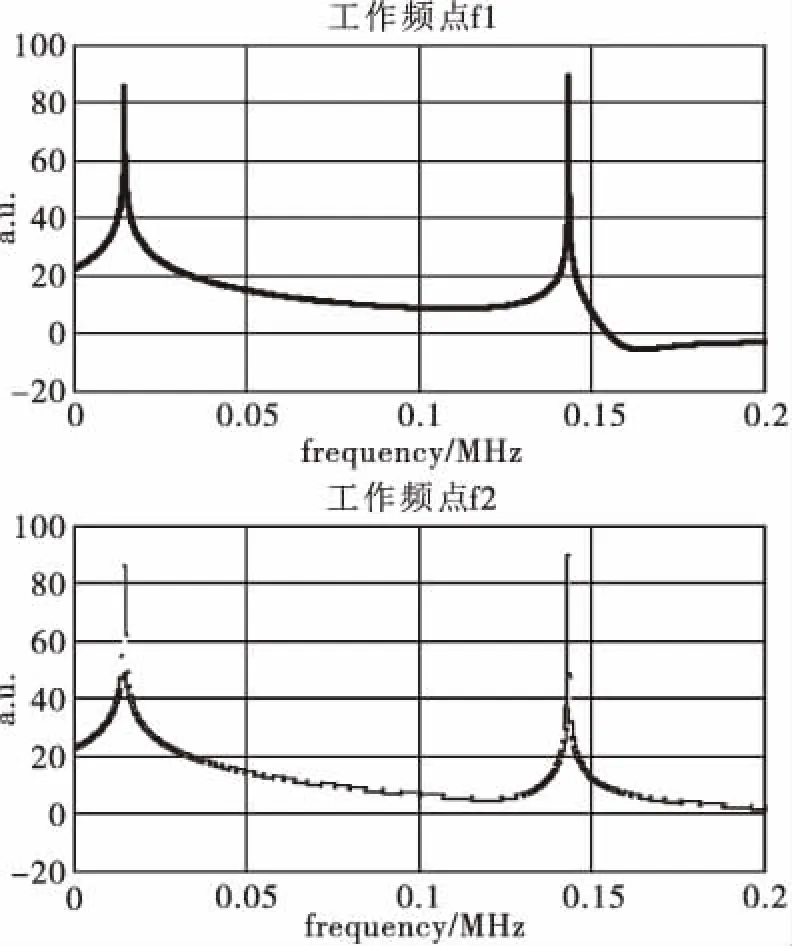
图3 不加噪声时，双频模目的频谱

图4为叠加噪声时，工作频点f1和f2下双频模目的频谱。由频谱分析结果，当工作频率为f1时FFT积累后两个目标的信噪比分别为38.09和38.10，扣除因积累增加的信噪比10×log10(65536)=48.16，两模拟目标回波的信噪比分别为-10.07和-10.06。对模目时域波形先进行相关处理，再进行频谱分析，可得到两目标的加速度分别为20.88m/s2和10.45m/s2。利用解算的加速度对目标回波进行补偿，再进行频谱分析，根据多普勒频率可得到两目标的速度分别为0.2199km/s和2.149km/s。

按照同样方法，当工作频率为f2时两模拟目标回波的信噪比分别为-9.96和-10.05，两目标的加速度分别为20.86m/s2和10.52m/s2，两目标的速度分别为0.2201km/s和2.150km/s。

计算目标的平均速度和平均加速度，并根据匀加速运动模型对目标回波进行补偿，再根据公式(9)可得到两模拟目标的距离分别为65.72km和120.1km。

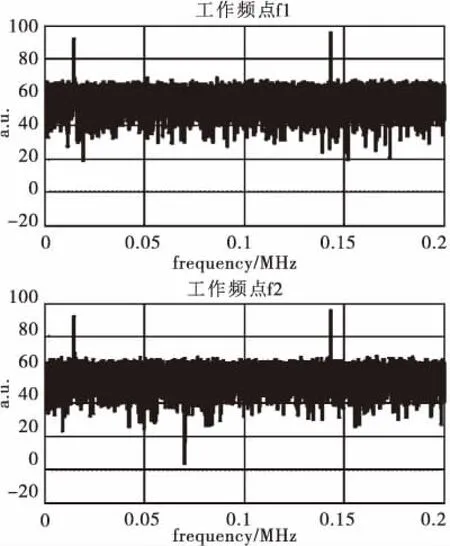
图4 叠加噪声时，双频模目的频谱

对模拟产生回波解算得到的目标参数重新列于表3。由表1和表3可知，计算结果与设计目标运动参数略有差异，这是由量化噪声和加性高斯白噪声带来的测量不确定性。

表3 解算的目标运动参数

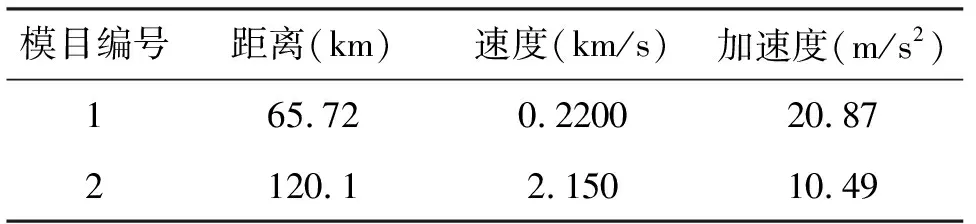
模目编号距离(km)速度(km/s)加速度(m/s2)165.720.220020.872120.12.15010.49

3 结束语

基于二次相差法等测距系统中对模拟目标回波的实际需求，设计了一种参数化的双频连续波模拟目标产生器。根据工程实现结果，解算的目标运动参数与设计参数在误差允许范围内，误差来源于量化噪声和加性高斯白噪声。整个系统具有可重配置和可动态扩展的特点，通过修改配置参数，模目产生器还可用于脉冲雷达产生参数化线性调频目标回波。