基于Duffing振子循环检测方法的研究
2019-04-11杨海博
杨海博 李 琳
(中国电子科技集团公司第二十研究所 西安 710068)
0 引言
传统信号检测方法一般以线性理论为主,即基于时域和频域分析,如应用广泛的频谱分析、Winger-Ville分布、小波分析方法等。这些方法在一定范围信噪比下,具有良好的检测性能,但在强噪声背景下弱信号检测中却具有局限性,特别当信噪比低至-10dB附近,传统线性理论检测性能急剧下降,甚至难以检测出待测信号[1]。
近年来,随着非线性方法在信息科学领域中的深入研究。人们开始将混沌理论用于弱信号的检测,在对待测信号有一定的预知的情况下,可较为精确的检测信号幅值、频率、相位等参数。
频率是信号的主要参数之一,也是人们常关注对象。基于混沌理论的频率检测方法主要有两种[2],一种是基于变形的Duffing振子检测法,另一种是基于Duffing阵法。前者需要对于待侧信号频率有一定的预知,实际应用中常难以对待测信号进行较为精确预知,后者所设置的阵元繁多、计算量巨大,且每个阵元都需要人工寻找系统阈值、误差波动,工程实现难[3-5]。
针对上述问题,本文在分析了间歇混沌检测信号频率的原理,给出了建立较小阈值的混沌系统方法,并引入循环思想,提出了一种计算机易于实现的混沌频率检测方法——基于Duffing振子的循环信号检测方法。
1 Duffing振子检测原理
Holmes型Duffing方程,其一般数学模型如下[6]:
(1)
式(1)中:rcos(t)为周期策动力;k为阻尼比;-αx(t)+βx3(t)为非线性恢复力。
先调节系统策动力幅值r,使得系统进入混沌运动状态(如图1)和大周期运动状态(如图2)的临界状态,得到阈值rd,再输入与系统策动力同频率的待测信号,系统便进入大尺度周期运动状态,这时调节系统策动力幅值r,使系统再次进入混沌运动状态和大周期运动状态的临界状态,得到此时的策动力幅值r′,则待测信号的幅值为f=rd-r′。
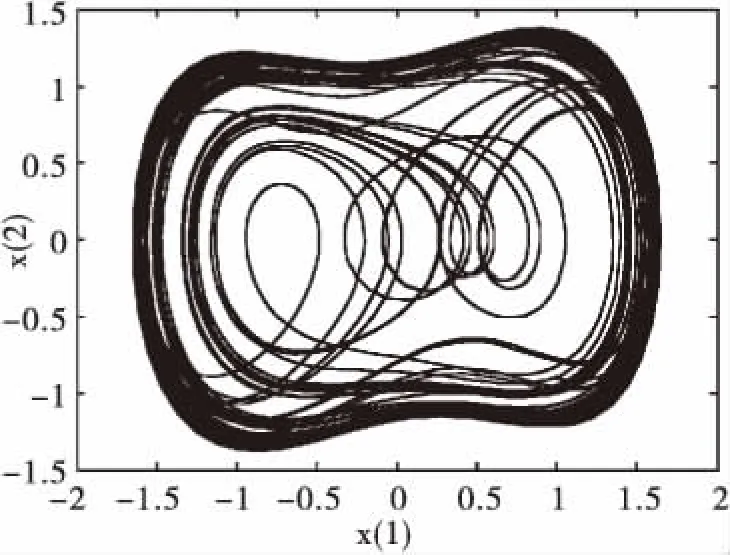
图1 混沌状态

图2 大周期状态
2 间歇混沌信号频率检测分析
Duffing振子系统中引入与其内置策动力之间存在一定的角频率差的微弱正弦周期信号,即[7]:
(2)
令r=rd,向式(2)系统加入一个任意微弱信号,无论此信号多么小,一定有r+a>rd。假设存在频差为Δω,系统总策动力为R(t),则:
=rcost+acostcos(Δωt+θ)-asintsin(Δωt+θ)+n(t)
=[r+acos(Δωt+θ)]cost-asintsin(Δωt+θ)+n(t)
=R(t)cos(t+φ(t))+n(t)
其中:
(3)
(4)
2.1 间歇混沌原理
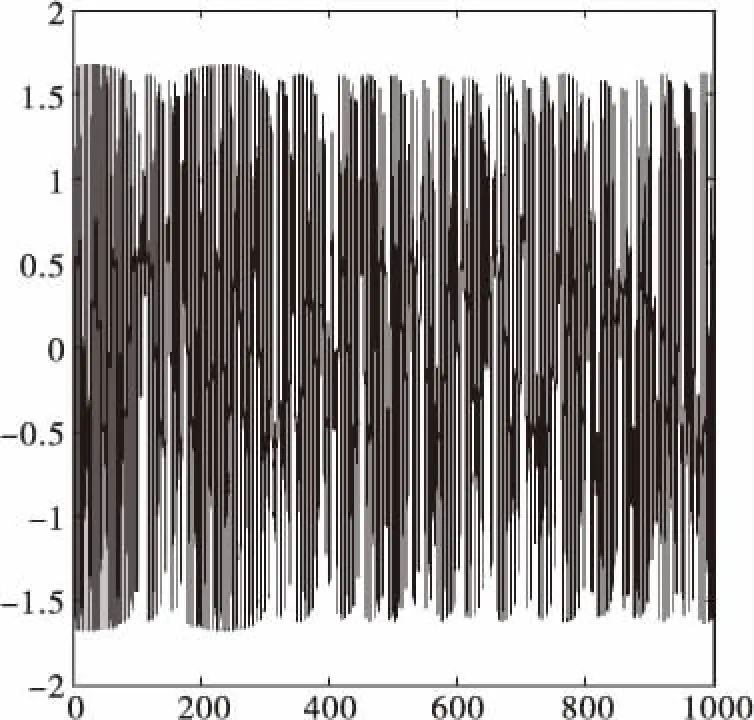
间歇混沌现象为待测信号与系统策动力存在频差情况下,出现的特有阵发混沌现象[8]。系统状态将呈现不同的变化,总策动力R(t)呈现周期变化,具体关系如图3所示。
当策动力与待测信号矢量夹角小于90°时,则其合成向量R(t)的幅值就会在某一段大于rd(系统阈值)区域内,系统处于大周期运动状态;当策动力与外界信号矢量夹角大于90°时,其合成向量R(t)某一段小于rd区域内,即R(t) 与此同时,我主动记下平时不懂的专业知识,遇到相熟的项目经理,抓住碎片时间积极上门请教,不躲闪不回避,主动提及双方在项目沟通上经常遗漏的部分,强烈表达增进双方沟通效率的愿望。通过积极主动的沟通,让项目经理意识到了我个人知识结构上的特点与不足,在后续的工作交流中更加体谅我个人的实际情况。这种互利双赢的勤学好问,赢得了项目经理的赞许,建立了更加融洽的关系。 由此可见,当策动力与待测信号存在频率差时,总策动力R(t)周而复始地大于或小于rd,即表现出间歇混沌状态(在非线性系统中,无论是时间上还是在空间上,间歇的出现混沌的现象,类似于规律性的周期运动)。即系统以一定的周期进行间歇混沌运动,间歇混沌周期: (5) 从式(3)可以看出,因racos(Δωt+θ)项影响,总幅值R(t)呈周期性变化。 (6) 当待测信号幅值a远大于或者远小于检测系统阈值r时,式(6)中周期项较非周期项占比η较小,R(t)变化周期较小,即系统难以出现间歇混沌,这表明周期项能量在整个检测过程中作用较小,难以驱动了检测系统进入显著间歇混沌状态,如图4所示。 当待测信号幅值a比检测系统阈值r者相差不大时,式(6)中周期项较非周期项占比η较大,R(t)变化周期较大,即检测过程中出现显著间歇混沌现象,这表明周期项能量在整个检测过程中作用较大,可以驱动检测系统进入显著的间歇混沌状态,如图5所示。 图4 混沌振子检测系统中加入0.01cos(1.03t)时系统时域图 图5 混沌振子检测系统中加入0.1cos(1.03t)时系统时域图 从以上分析可以看出,但凡基于间歇混沌现象检测信号频率,必须保持混沌系统阈值与被检测信号在一个数量级上或者相差不大,即要检测微弱小信号,必须选用阈值比较小的混沌系统。 混沌系统。如何建立阈值较小的混沌系统,成为了能否成功检测到微弱信号频率的关键。 通过多次仿真计算发现,线性系数α越小,阈值也越小;非线性系数β越大,阈值越小,当β=1时,系统阈值与参数α的变化如图6所示,当α=1时,系统阈值与参数β的变化如图7所示。 常规的间歇Duffing阵检测法存在的主要问题: 1)一般建立阵元数量庞大,不易计算机计算; 3)将间歇混沌间歇周期最大的阵子策动力频率作为待测信号频率,误差较大。 基于Duffing振子的循环检测系统,剔除了大量阵元的建立,避免了不同的策动力重新设定阈值,采用计算机易于实现的循环算法。 基于Duffing振子的循环检测法检测未知微弱信号的步骤如下: 第一步,对待测信号进行预处理,判断信号频率数量级,选择合适的循环混沌检测系统; 第二步,调节系统处于混沌与大周期状态的临界状态,设定系统循环初始值,选择策动力频率循环迭代步长,加载间歇混沌现象记录程序; 第三步,提取各显著间歇混沌周期,计算被测信号频率,并求均值,均值即为被测信号频率。 图6 基于Duffing阵子循环检测系统流程图 图7 检测纯信号时,记录程序记的间歇混沌现象 图8 检测带噪声信号时,记录程序记间歇混沌现象 观察图9、图10不难看出随机噪声的加入使得原来很光滑的输出变得粗糙,但未破坏间歇混沌现象,可以明显看出间歇周期,从而通过软件程序计算出待测信号频率。 为验证基于Duffing振子的循环检测方法性能,本试验在强噪声下(信噪比-40dB),对比新方法与传统Duffing阵法检测性能,以及计算速度。 调整Duffing检测系统基本参数,降低检测系统阈值,选用与待测信号同一数量级的阈值的检测系统。 选用k=0.5,α=0.04,β=3000参数,预置系统周期策动力角频率为1。建立Duffing振子检测系统: (7) 经过仿真得到此系统阈值为rd=0.0103。 待测信号模型为: s(t)=0.01cos(1.09t)+n(t) (8) 其中n(t)为均值为0,方差为1的高斯白噪声。 方法1:建立Duffing振子阵,含阵元10,各振元策动力频率为ω、1.03ω、1.032ω…1.039ω,并将各阵元调至系统混沌到大周期的临界阈值。 方法2:建立基于Duffing振子的循环检测系统,循环步长0.03,并设置程序自动记录(记录显著间歇混沌数据)。 图9 混沌阵第4个阵元的间歇混沌现象 图10 循环检测法记录程序记录的间歇混沌现象 通过方法1,对各阵元进行仿真计算,发现阈值为0.944的阵元混沌间歇周期最大,如图11,由式(5)可知,间歇周期越大,检测系统策动力与待测信号频率越接近,可认为该策动力频率就是待测信号频率。因此认为待测信号频率为1.0927,检测误差为0.25%。 通过方法2检测,按照图6流程,提取的间歇混沌现象,如图12,对于各间歇混沌的周期进行均值处理,均值为1.0901即待测信号频率为1.0901,检测误差为0.09%。且计算速度远快于方法1。 通过与传统方法对比不难看出,在-40dB的信噪比下,基于Duffing振子的循环检测法微弱信号检测性能优于传统混沌阵法,且计算速度远快于方法1。 本文分析了间歇混沌基本原理,推导了待测信号幅值大小对于间歇混沌现象的影响,给出了通过调整检测系统参数来调低阈值的解决方法,提出了基于Duffing振子循环检测方法步骤,并对-40dB信噪比下弱信号进行验证,结果表明新方法检测精度优于传统方法。2.2 待测信号幅值对间歇混沌的影响

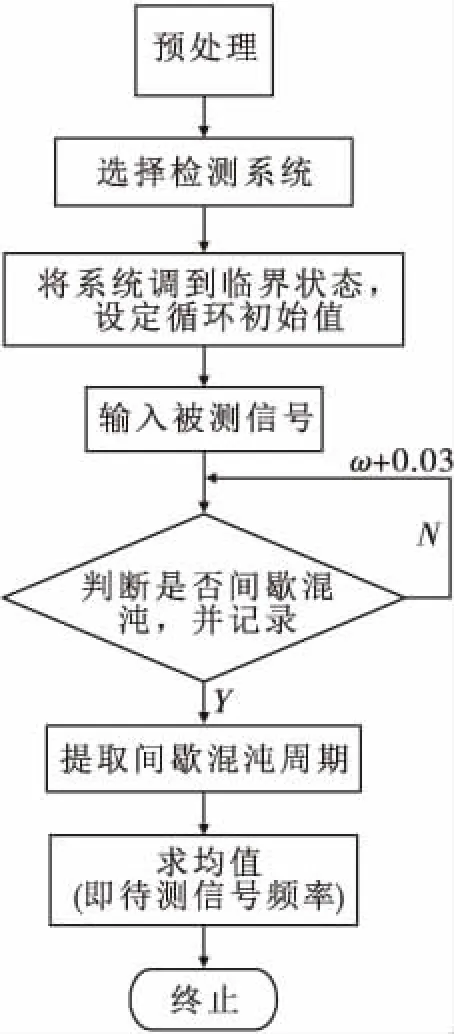
3 基于Duffing振子的循环检测系统


4 仿真分析


5 结束语
