一种基于功能安全的电机控制位置检测算法改进
2019-04-10王瑛强巨光
王瑛,强巨光
(奇瑞新能源汽车技术有限公司,安徽芜湖 241002)
0 引言
永磁同步电机(Permanent-Magnet Synchronous Motor,PMSM)因具有效率高、损耗小、结构简单、运行可靠等优点,在新能源汽车行业取得了广泛的应用[1]。现如今新能源汽车电驱动系统常用的控制算法为FOC矢量控制算法,该算法依赖转子的速度、位置信号等参数参与控制计算。因此需要在转子侧安装位置传感器用以检测电机转子的转速、位置角等信息。
常见的位置传感器有旋转变压器、正交编码器等。其中正交编码器是一种通过光电转换将转子的位移转换成脉冲或者数字量的传感器,可以高精度地检测被测物体的转角等信息[2-3]。因其具有精度高、体积小、性价比高等优点成为目前应用最多的传感器之一。
根据光电编码器产生的脉冲方式不同,可将其分为增量式、绝对式以及复合式三大类。其中增量式编码器通过输出A、B两相互差90°的脉冲信号(即两组正交输出信号),从而可判断旋转方向。而参考零位的Z相脉冲则在码盘每旋转一周发出一个脉冲信号用来对积累量清零[4]。
增量式编码器常见的测速方法有M法、T法和M/T法3种[5-6]。其中M/T法是同时对光电编码器输出的脉冲个数M1和M2进行计数,则电机每分钟的转速为
式中:N为编码器的线数;fclk为时钟频率。文中所采用的编码器线数为2500线。
正交编码器提供了电机控制过程中重要的角度信息,但其复杂的机械结构导致其在实际的应用中经常出现故障,尤其是在高速行驶过程中,若正交编码器输出不准确或因故障导致传感器不能工作,会直接导致电流、扭矩等出现问题。此时车辆无法正常工作,只能停机下电,存在极大的安全隐患。针对这一工况,本文作者提出了一种新的提高电动汽车驾驶安全系数的改进方法,在传统的FOC控制算法基础上,增加一个滑模观测(Sliding Mode Observer, SMO)系统。在电机运行过程中,实时监测正交编码器的工作状态,一旦判断其输出信号出现异常或编码器出现故障时,及时将位置监测信号切换到滑模观测(SMO)系统,此时采用SMO算法估算电机转子的位置和速度来控制电机的运行,使得电动汽车不会立即停止工作。在SMO算法的支持下电动汽车处于跛行模式,可由驾驶员驾驶至安全区域或者维修点。
1 滑模控制系统的原理及设计
永磁同步电机系统分析比较复杂,因此需将其数学模型进行简化。假设电机的定子绕组为Y形接法,且三相绕组为对称分布,气隙磁场的分布亦不受齿槽的影响,铁心的磁导率为无穷大,忽略涡流损耗和磁滞损耗[7]。
1.1 滑模观测器的设计
永磁同步电机(PMSM)在静止的α-β坐标系下有:
(1)
(2)
式中:iα、iβ、eα、eβ分别为电机在α-β下的α轴和β轴的电流和电机的反电动势;R为定子电感;L为相电感;Ψf为永磁体磁链;ωe为电机的转速。由式(2)可知,通过求得PMSM的反电动势即可以反向推出电机的转速和位置角信息。
为了提取电机的转速、角度等信息,根据滑模观测器的控制原理,通过对反电动势的跟踪计算,设计出一个新型的基于抗饱和函数的滑模观测器,其状态方程如下:
(3)
式中:Iα、Iβ、uα、uβ分别为定子电流在α-β轴上的电流估算值和反电动势估算值。
饱和函数表达式为
(4)
式中:Hα、Hβ为切换信号;ksw是滑模观测器的滑模系数。
定义滑模面为
(5)
由式(4)—(5)可得出饱和曲线函数如图1所示。
此处Δ为边界层,从图1可以看出,该控制模型在S=Δ和S=-Δ处各有一个切换面。在[-ΔΔ]内饱和曲线是线性函数。
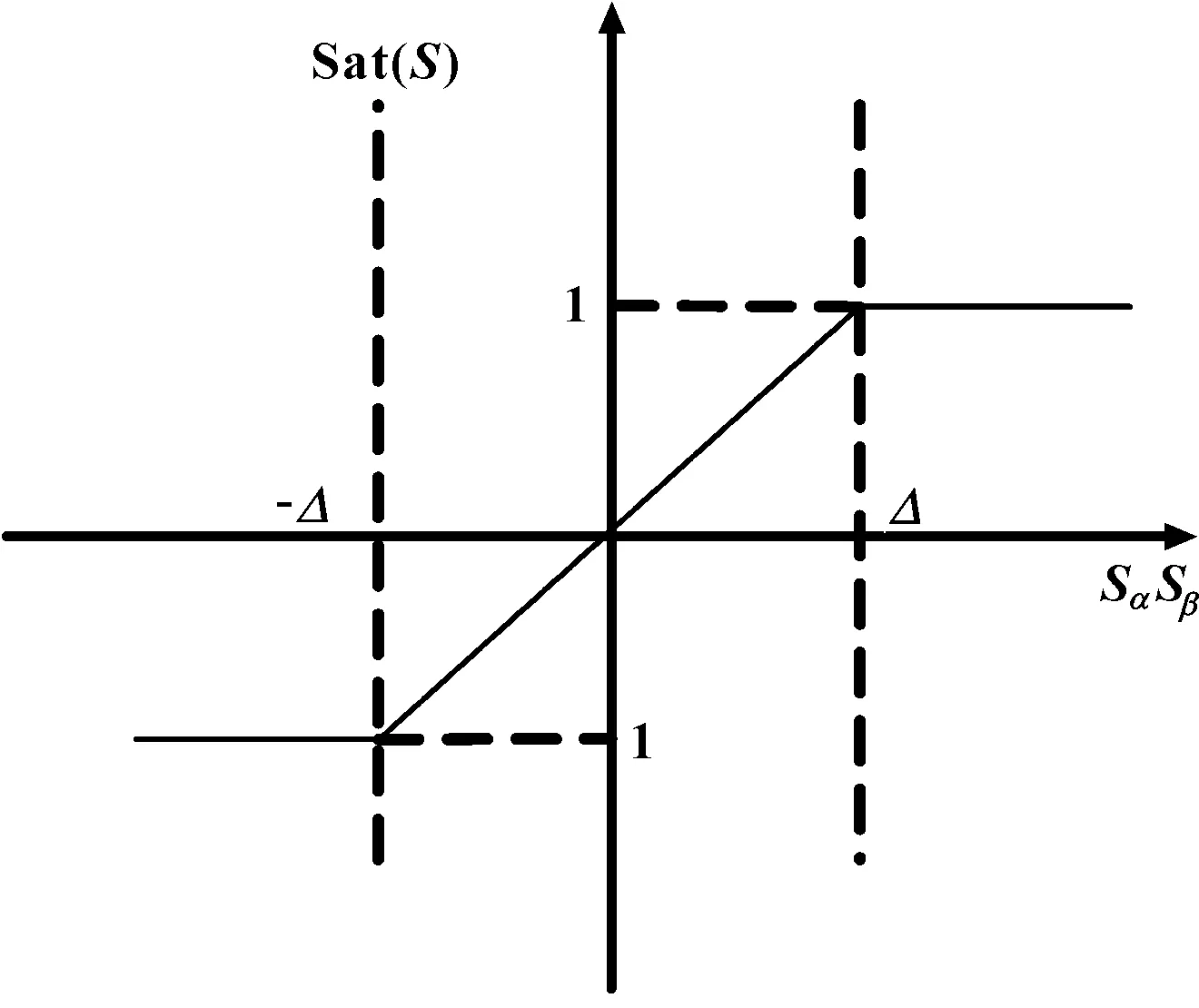
图1 饱和曲线函数
在(-∞,-Δ)∪(Δ,∞)内函数值为1,因此饱和曲线函数表达为
(6)
通过选择合适的Δ值,可以大幅降低滑模控制的抖动,使用此饱和函数替代开关函数,可以有效地降低系统的波动。尤其是在较大转矩脉动或低速情况下的抖动情况能得到明显地改善。
1.2 电机转速及位置的估算
由电机的反电动势公式(2)可分别求得电机角度和转速为
(7)
(8)
因计算转速和转角,需要对式(7)进行求导来计算反电动势,但是因为系统的采样频率、Bang-Bang控制产生的高频干扰信号等,所以需要设计一个低通滤波器进行信号滤波。但受低通滤波器的影响,会导致相位出现延迟。为了提高算法的准确性必须对系统进行相角补偿,具体的可通过建立一个相位延迟表,通过查表法求得在已知转速下的相位延迟。
根据上述滑模观测器原理,通过MATLAB/Simulink建立相应的滑模观测器系统算法模型,如图2所示。
图3通过计算电机控制过程中的Valpha、Vbeta、Ialpha、Ibeta等参数最终输出电机当前的电角度θ和转速。
滑模观测器搭建后将其集成到传统的基于旋变信号的永磁同步电机仿真模型中进行调试验证。总体系统仿真模型如图4所示。
电机采用埃斯顿公司的EMJ-04APB22,其参数为额定功率0.4 kW,额定扭矩1.27 N·m,电子电阻0.18 Ω,反电动势常数5.183×10-2(V·min)/r,电感Ld和Lq皆为0.000 835 H,电机磁链为0.071 439 4 V·s。从图2可知,系统主要分为FCO算法模块、SMO模块和传统的基于位置传感器的转速和转角检测模块。Data Store Read模块为Simulink基本模块,其与Data Store Memory、Data Store Write协同工作可实现不同模型之间数据的传递。当在旋变发生故障时,故障信号通过Data Store Write写入Data Store Memory中,Data Store Read模块检测到Memory变化后将故障信号传递给图2中的Switch模块。将电机角度的输入由旋变信号切换至滑模观测器。保证了汽车在旋变发生故障情况下不会立即停车,仍能启动跛行模式行驶至安全区域或者维修站,从而提高了驾驶安全性以及便利性。
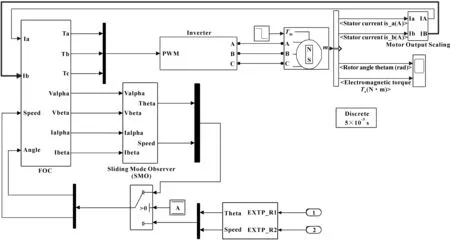
图2 永磁同步电机整体算法仿真模型

图3 滑模观测器仿真图
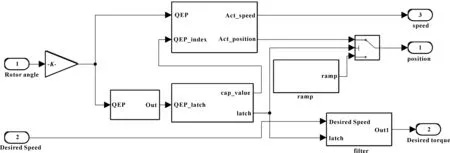
图4 滑模观测器系统仿真模型
为了验证搭建系统的可靠性,该实验分为仿真验证和实物验证两部分。
1.3 仿真验证
根据正交编码器的测速原理,在MATLAB中,将电机输出角度作为正交脉冲计数值,通过对其进行处理得到正交脉冲计数处理后的转子位置信息与转速信息。在此选择一个2500线的增量式编码器作为转速、位置等的检测模块。其仿真模型如图4所示。
在电机起步阶段因为系统无法判断电机的零位与当前编码器的关系,故给其一个较小的斜坡爬升角度和起步扭矩。待系统检测到零位信号QEP_index(Z相脉冲)时,将实际的电机位置信号值和扭矩命令值作为输入值。其仿真结果如图5—图6所示。
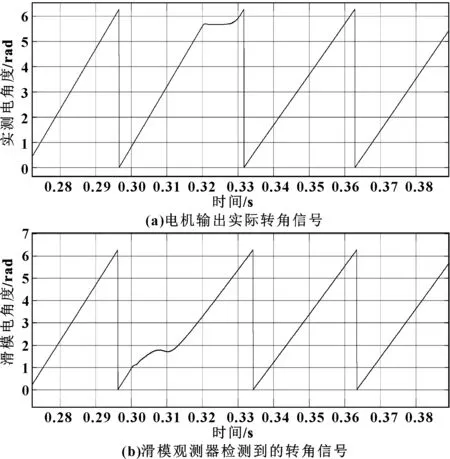
图5 滑模观测位置角度和实际对比

图6 滑模观测转速和实际转速对比
图5(a)为电机输出实际转角信号,图5(b)为滑模观测器检测到的转角信号。图6(a)为电机实际转速,图6(b)为滑模观测器检测到的转速。可知其信号基本吻合,证明基于模型设计的滑模观测器是合理的。
通过MATLAB内置的Embedded Coder 模块将SMO的仿真模型生成C代码,集成到传统的基于旋变信号的检测代码中。通过TI的编译软件CCS生成Out文件下载到开发板中实时运行,检测滑模观测系统和位置传感器检测到的位置信号的差异。其结果如图7所示。图7(a)为滑模观测器估算出的转角位置,图7(b)为旋变信号检测到的转角位置。两者的频率与变化曲线基本重合,能满足电机控制的要求。
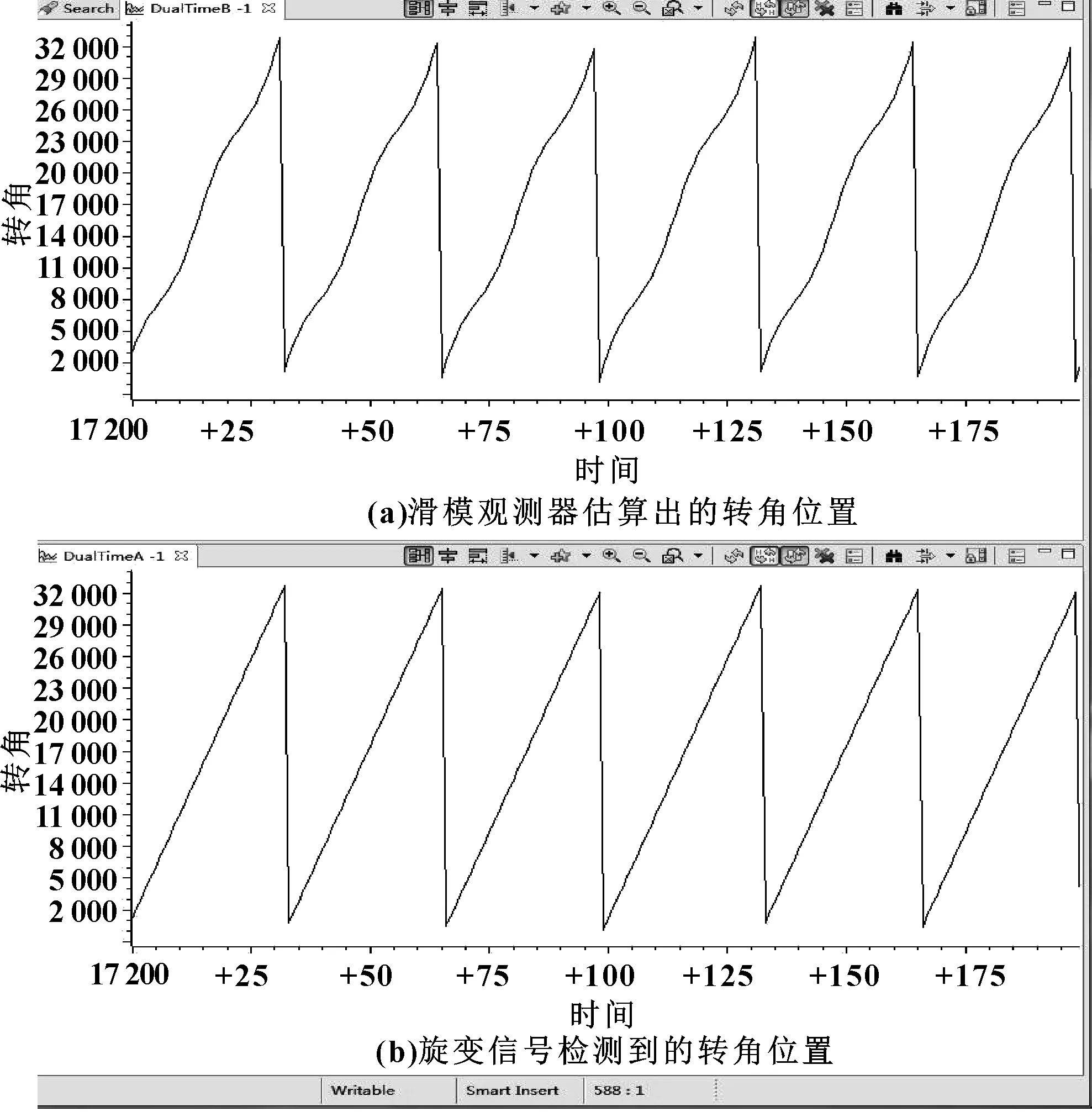
图7 滑模观测器估算和传感器检测电角度
2 结束语
现已验证了滑模观测器在模型仿真和实际运行中检测的准确性,为了模拟在实际运行中旋变出现故障无法解析角度而启用滑模观测器,定义一个变量Fault flag赋值给Data Store Write。当旋变正常工作时Fault flag为零,FOC算法所采用的转子信息值为旋变提供;当旋变装置发生故障时,将Fault flag设置为1,此时将滑模观测器估算的转子信息作为变量传递给FOC算法用以计算控制电机。
经过仿真及实际验证,在旋变信号发生故障时,滑模观测器所检测的转子位置信号能有效地替代旋变信号,维持电机的正常工作,避免了紧急停车的情况,极大地提高了乘客的安全性能,能满足整车越来越高标准的功能安全规范。
