等寿命曲线的变截面钢板弹簧可靠性分析方法
2019-04-08卢剑伟王翔宇李海波
张 洁,卢剑伟,王翔宇,李海波
(1.合肥工业大学 汽车与交通工程学院,合肥 230009;2.江淮汽车股份有限公司 技术中心,合肥 230601)
钢板弹簧是汽车悬架中常见的弹性元件,由于其结构简单,成本较低,被广泛应用于载货汽车和部分采用非独立悬架的客车上[1]。钢板弹簧主要分为普通多片钢板弹簧、变截面钢板弹簧、两级变刚度钢板弹簧和两级变刚度复式钢板弹簧等[2]。同等质量下,变截面钢板弹簧能够储存更多的弹性势能,从而节省材料,使用更为广泛[3]。
为了研究变截面钢板弹簧的弯曲应力分布并预测其疲劳寿命,将有限元方法广泛用于钢板弹簧的分析和设计优化中[2-5]。在不同的载荷工况下,簧片的几何特征可能会发生较大变化,其应力分布也将改变。而且,结构参数对应力分布和疲劳寿命有很大影响,设计者要反复改变结构参数并建立有限元模型从中寻找最优簧片参数值,模型建立和计算的工作量大从而延长了研发周期[3,6]。因此,提出简化计算模型对于研究变截面钢板弹簧的弯曲应力分布和预测其疲劳寿命具有重要意义。
本文在前期研究的基础上提出一种简化的计算方法,可以较为便捷地计算分析变截面钢板弹簧弯曲应力的分布情况,并分别以弯曲簧片和平直簧片在不同载荷工况下的弯曲应力分析为例,通过算例对该计算分析方法进行了对比验证。结合Goodman直线修正公式和钢板弹簧材料的P-S-N曲线绘制出不同交变力下的疲劳寿命等值线图。通过算例验证了结果的准确性,且提出的计算分析方法精度较高、计算快速便捷,充分满足了工程应用的要求,相关研究方法有助于缩短变截面钢板弹簧的设计研发周期。
1 考虑变截面钢板弹簧弯曲时的应力分布
变截面钢板弹簧初始弯曲时所承受的均布载荷如图1所示,其中簧片中部板簧座承受U型螺栓夹紧力。本文将U型螺栓承受的力简化为均布载荷和集中载荷两种情况,基于Timoshenko梁理论计算沿簧片长度方向的弯曲应力分布。其中簧片两端卷耳处铰接可沿水平方向自由运动,簧片中间受到U型螺栓夹紧后等效载荷。钢板弹簧详细数据见表1。
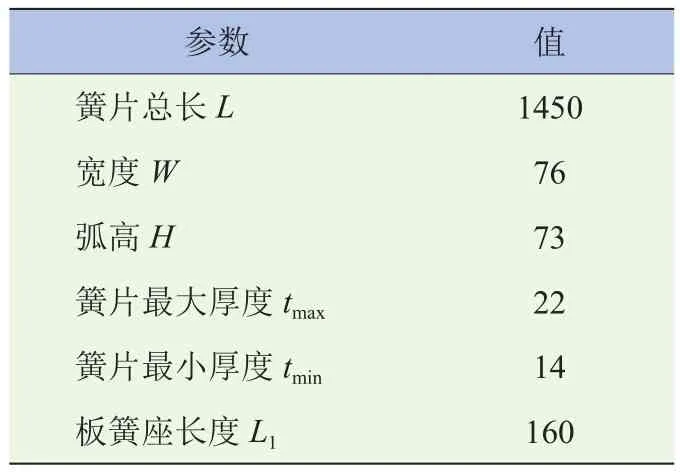
表1 钢板弹簧参数表 mm
假设梁的纵向对称面内只作用大小相等、转向相反的一对力偶,使梁产生纯弯曲变形,此时梁的横截面上只有弯矩,所以只存在与弯矩相关的正应力[7]。为了简化模型,忽略梁的剪切应力,只考虑与弯矩相关的弯曲正应力。
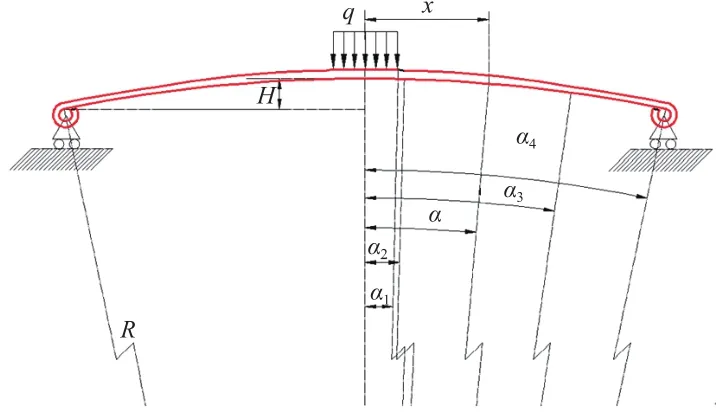
图1 变截面钢板弹簧初始弯曲时承受的均布载荷
如图1所示,簧片弧高为H,簧片总长为L,U型螺栓夹紧区域为转角−α1至+α1且受到均布载荷q的压力。因簧片为对称结构,取图中对称结构右侧区域,当0<−α1<−α1时(图2),簧片截面厚度h为定值;当−α1<−α1<−α13时,簧片截面厚度h为变量,即簧片出现变截面性质;当−α13<−α1<−α14时,簧片截面厚度h为定值。
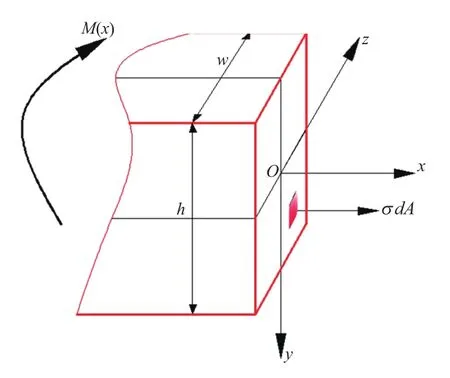
图2 钢板弹簧截面示意图
由材料力学可知,截面处的弯曲正应力为:

式中:M(x)为横截面上的弯矩;W为抗弯截面系数,与截面的几何形状有关。簧片为左右对称结构,现分别计算当−α4<α<−−α14时,簧片所受到的剪力Fs。
当−α4<α<−α1时,
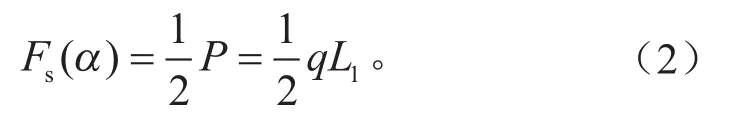
当−α1<α<−−α1时,

当−α1<−α1<−α14时,

因为,

所以,当−α4<α <−α1时,
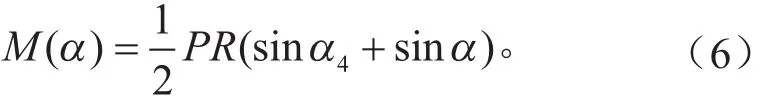
当−α1<α <−α1时,
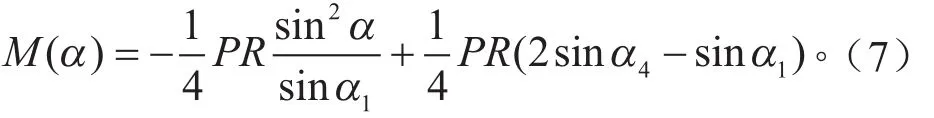
当−α1<−α1<−α14时,
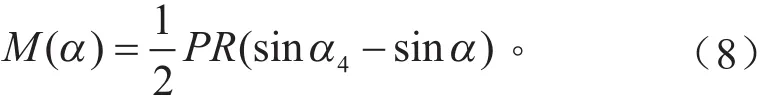
由于该钢板弹簧的变截面性质,当α ∈ (− α4,−α3)∪(α3,α4)时,矩形截面的高度h(α ) =tmin; 当α∈(− α1,α1)时,h(α ) =tmax。其它区域钢板弹簧截面高度可以利用多项式拟合得出,方法不再赘述。由此得到钢板弹簧随转角α变化时的弯曲正应力分布的数学表达式。
取0<α< α14的板簧右侧二分之一模型为例。
当0<α < α1时,
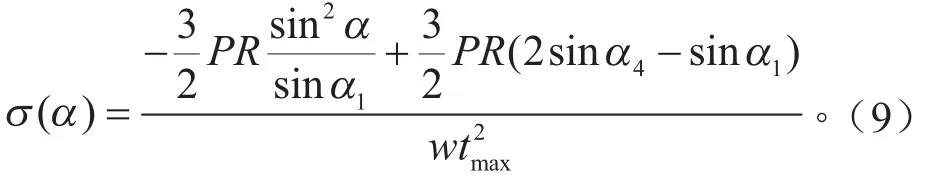
当α1<α <α2时,
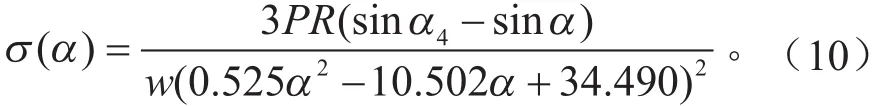
当α2<α <α3时,
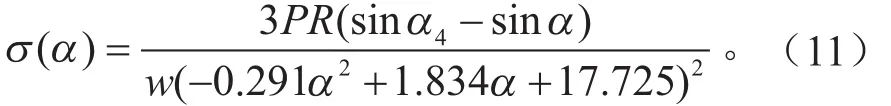
当α3<α<α4时,

簧片左侧区域弯曲应力分布与上述求解方法一致。至此,弯曲簧片受到均布载荷夹紧力的弯曲应力分布数学表达式已建立。同理,当U型螺栓夹紧簧片时,假设簧片承受集中力P,作用点为板簧座中部。按上述方法,同样可以得到随转角α变化时簧片弯曲正应力的表达式。不同于簧片承受均布载荷,当−α1<α<−α1时,弯矩值与上述模型不同。
当 −α1< α1< 0时,
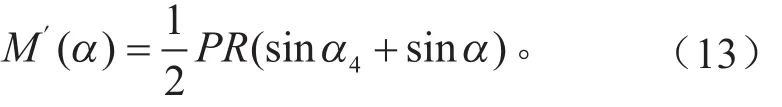
当0<α< α1时,
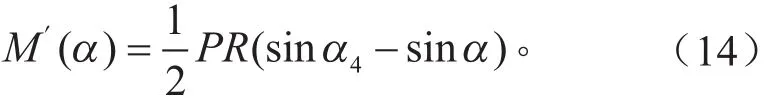
所以,当−α1<α<0时,
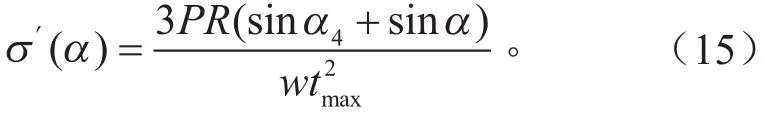
当0<α< α1时,

其它区域弯曲应力表达式与簧片承受均布载荷时一致。
2 考虑变截面钢板弹簧平直时的应力分布
钢板弹簧在制造过程中常被加工成弯曲梁形式,受到外载时,板簧由于形变会导致初始弧高发生变化[1]。现建立平直钢板弹簧及其板簧座处承受均布载荷时的计算模型,以探究簧片初始平直时的弯曲应力分布情况。变截面钢板弹簧平直时承受的均布载荷力如图3所示。由于该簧片的变截面特性,所以将簧片沿长度变化方向分为数段,便于研究其弯曲应力分布。与上述求解初始弯曲时的方法相同,经理论推导可知该簧片不同位置处的弯矩值和应力分布。
当0<x<l3时,

当l3<x<l4时,
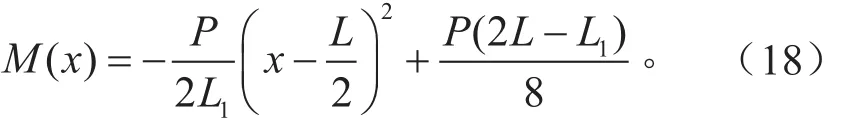
当l4<x<L时,
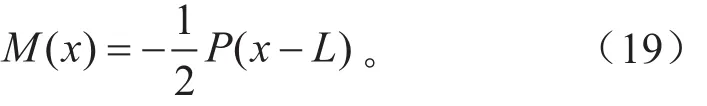
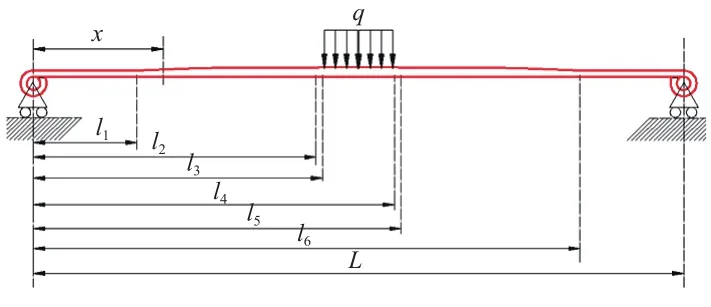
图3 变截面钢板弹簧平直时承受均布载荷力
同理,由于每段板簧的截面高度不同,所以每段弯曲应力由分段给出。
当0<x<l1时,

当l1<x<l2时,
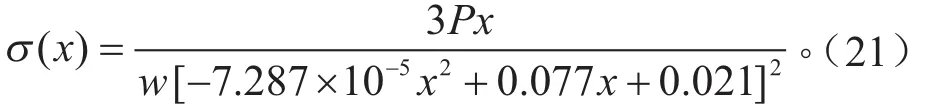
当l2<x<l3时,

当l3<x<l4时,
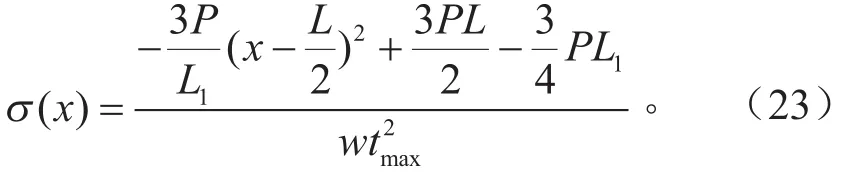
当l4<x<l5时,
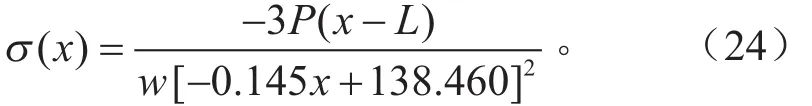
当l5<x<l6时,
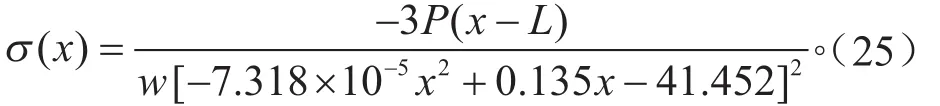
当l6<x<L时,
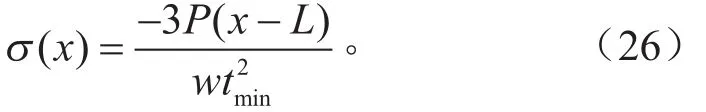
3 变截面钢板弹簧有限元仿真与模型验证
将上述建立的计算分析模型与有限元模型结果进行对比。由供应商处获得钢板弹簧的材料性质参数,具体值见表2。

表2 钢板弹簧的材料性质参数
有限元模型的约束采用两端卷耳可沿水平方向自由移动的方式。网格为六面体,网格尺寸为5 mm。在ANSYS软件中建立有限元模型,并通过板簧座施加U型螺栓均匀分布的夹紧力P,求解钢板弹簧弯曲主应力,其结果如图4所示。

图4 变截面钢板弹簧的有限元弯曲应力结果
在Matlab中依次绘制出上述计算分析模型和有限元模型的弯曲应力值,如图5所示。

图5 计算模型和有限元模型的弯曲应力值
由图5可知,簧片承受的均布载荷显著降低了板簧座应力集中现象处的应力峰值。四种结果都表明,在距卷耳约230 mm、630 mm和645 mm处均出现明显的应力集中现象,经查证,该处同为簧片的变截面过渡区域。为了降低应力集中处的应力峰值,簧片的设计加工应为较平缓的截面过渡,这与实际情况吻合。
分别将建立的各个数学公式模型应力结果与有限元模型应力结果进行对比(表3~5)。

表3 有限元与弯曲簧片均布载荷应力值对比

表4 有限元与弯曲簧片集中载荷应力值对比
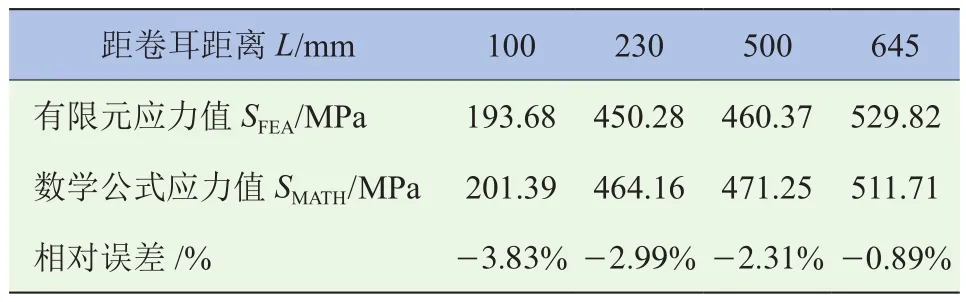
表5 有限元与平直簧片均布载荷的应力值对比
由表可知,建立的数学表达式求解弯曲簧片均布载荷的应力值和有限元应力值相对误差较小,其中,在距卷耳100 mm处,两者相对误差为-2.24%,在距230 mm、500 mm和645 mm处的相对误差分别为-1.19%、-0.63%和0.84%,而且两者在应力集中处的结果也十分接近。因此,建立的计算分析模型可代替该簧片的有限元模型并用于后续分析。
弯曲簧片受到等效集中力在距卷耳645 mm处(此处为应力集中点)的相对误差为2.13%,整体应力分布有明显的应力集中现象,精度稍逊于均布载荷工况下的弯曲簧片。
对比发现簧片平直状态下的整体应力分布值显著高于簧片弯曲状态下的应力值,这也间接表明弯曲情况下的钢板弹簧有较好的储存弹性势能的能力[3]。在设计初始应考虑自由状态下弧高对弯曲应力分布的影响。因此,通过改变模型中弧高数据,可快速得到簧片中任意一点应力值的变化。距一端卷耳230 mm、630 mm和645 mm处的应力值随弧高变化情况如图6所示。
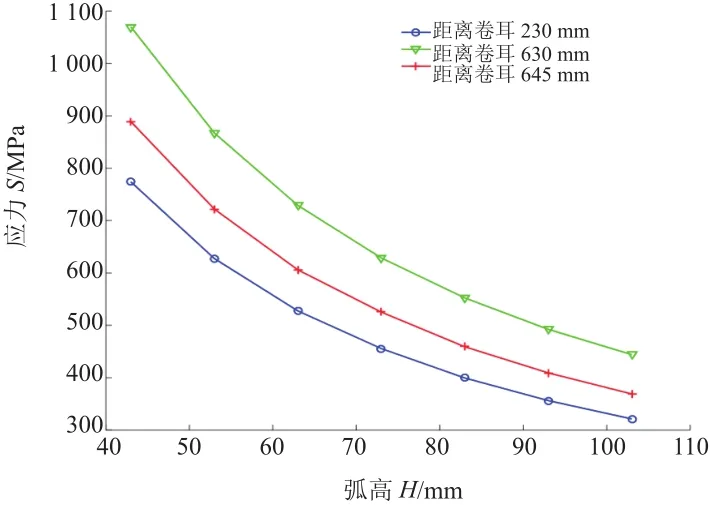
图6 10 000 N载荷下应力值与弧高变化情况
由图6可知,不同点的应力值与弧高有明显非线性关系,当弧高变大时应力值逐渐变小。
4 钢板弹簧疲劳可靠性分析与等寿命图绘制
由于疲劳寿命本身具有统计意义,所以根据材料在不同存活率下的S-N 曲线来估算零件在此存活率下的使用寿命[8]。该簧片采用的材料是60Si2Mn,根据该材料的 P-S-N 试验曲线,以双对数线性函数拟合如下:

式中:P为存活率;σ为对称应力幅;Np为在此应力水平作用下存活率为p时的疲劳寿命;ap、bp为拟合参数。各存活率下具体参数见表6[9]。
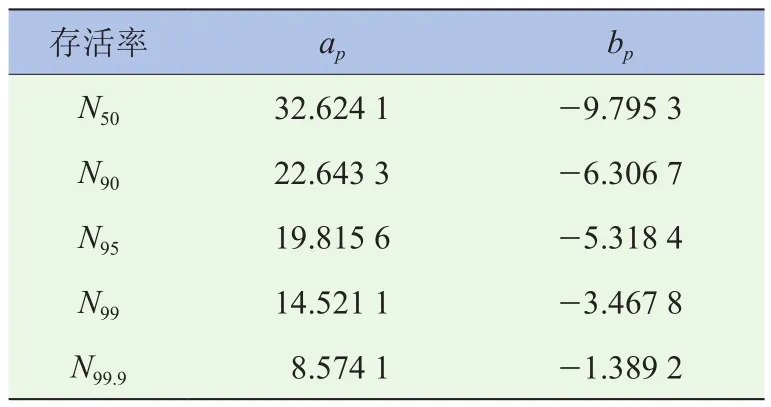
表6 不同存活率下S-N曲线拟合参数
材料的S-N曲线是基于均值为0的载荷确定的,平均应力对疲劳损伤计算结果有较大的影响。本文采用工程中应用较为广泛的Goodman直线修正法进行修正计算[10]。
由图5可知,不同模型均表明簧片在距卷耳230 mm、630 mm、645 mm处时有明显的应力集中现象。现取3处有应力集中现象的点,再加上板簧座中心(该处距卷耳725 mm)共4处疲劳热点,预测其疲劳寿命。
根据Goodman直线修正公式和钢板弹簧材料的P-S-N曲线得出某一循环次数下的应力均值和幅值,再根据上文建立的计算分析模型中载荷与应力的对应关系,得出4处疲劳热点在某一应力下的载荷均值和幅值响应。由此得出当存活率为50%、循环50万次的疲劳寿命,如图7所示。
经核算,距卷耳630 mm、承受相等交变力时的疲劳寿命是4处疲劳热点中的相对最低点。以该点为疲劳热点,当存活率为90%和50%时,得出该簧片在不同循环次数下的等寿命曲线图,如图8和图9所示。
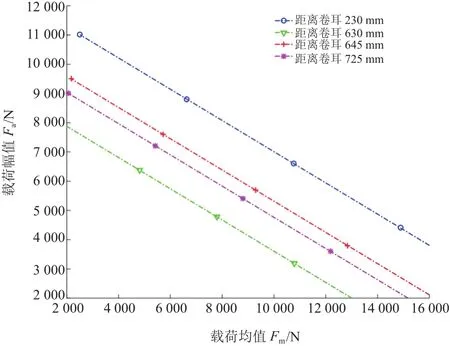
图7 四处疲劳热点在50%存活率下50万次循环寿命图
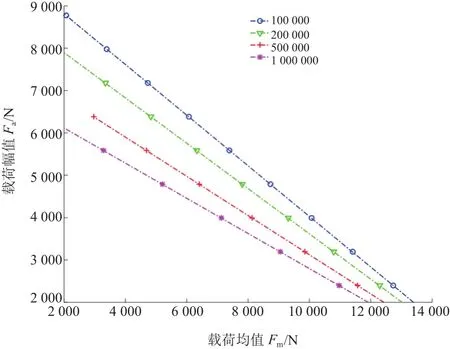
图8 90%存活率下的钢板弹簧等寿命曲线
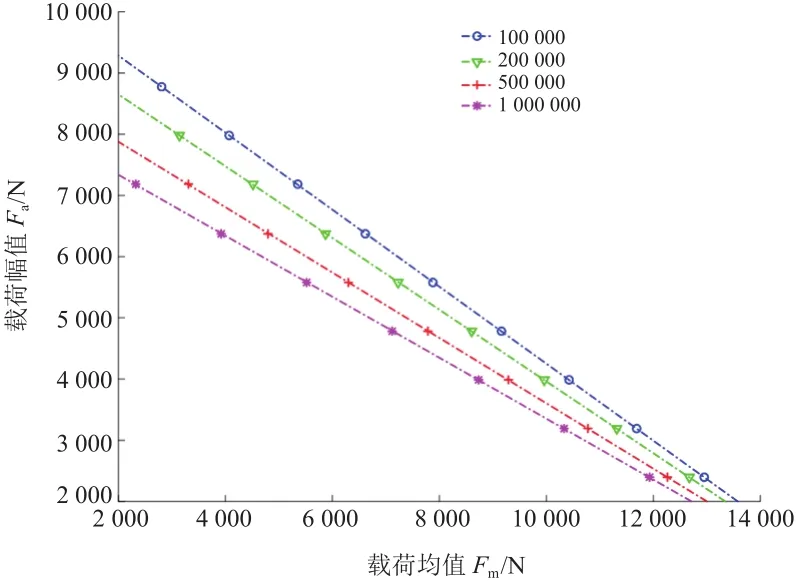
图9 50%存活率下的钢板弹簧等寿命曲线
同理,可得出当循环次数为20万次时不同存活率下的钢板弹簧寿命曲线,如图10所示。
在有限元软件ANSYS中建立疲劳分析模型,以验证上述等寿命曲线的正确性。在部分载荷均值和幅值的加载下,计算距卷耳630 mm处的循环次数,并与等寿命曲线图结果对比,见表7。
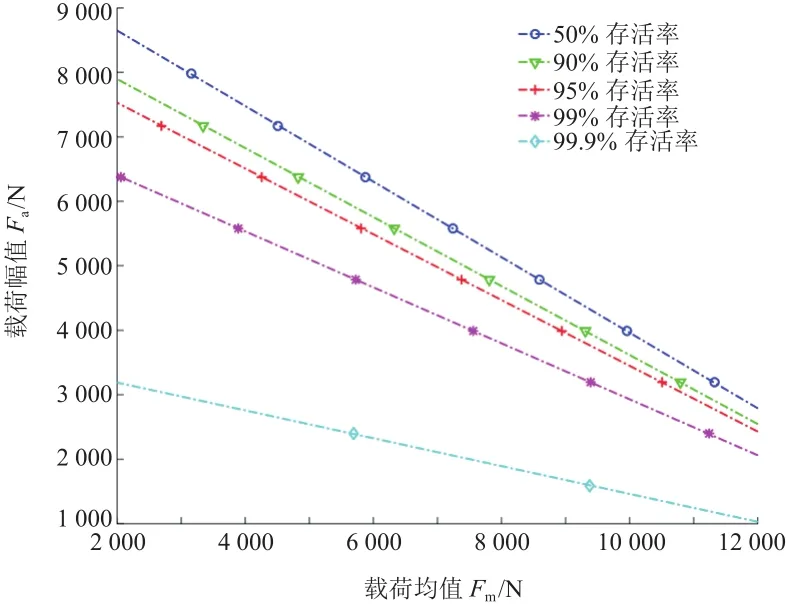
图10 20万次循环不同存活率下的钢板弹簧等寿命曲线

表7 等寿命曲线图循环次数与有限元寿命循环次数对比
由表7可知,等寿命曲线图得到的循环次数比有限元计算结果略小。原因是前文推导的弯曲应力公式计算值比有限元计算结果小,因此由式(27)和Goodman直线修正公式计算得出的循环次数比有限元计算结果偏小。有限元计算结果也表明整个簧片最低寿命点为距卷耳630 mm的变截面处,这与前文分析吻合。从本次的对比结果可知,等寿命曲线图和有限元分析的误差约在10%左右,表明等寿命曲线图结果偏于保守,这也进一步证明了等寿命曲线图的合理性和准确性,由此可见计算分析模型可满足工程应用精度要求并大幅降低计算时间。
5 结论
本文建立变截面钢板弹簧计算模型求解弯曲簧片和平直簧片在不同载荷工况下的弯曲应力,并与有限元分析结果进行对比。根据疲劳寿命准则和建立的计算分析模型,绘制出该钢板弹簧的疲劳寿命等值线图,可以得到以下结论:
(1)提出了一种适用于变截面钢板弹簧的等疲劳寿命分析方法,并给出了具体流程,算例与计算结果表明该方法精度较高。该疲劳寿命分析方法既能正确反映钢板弹簧的疲劳性能,又能大幅度降低计算时间、缩短设计周期,是类似零部件可靠性分析的有效手段。
(2)建立精度满足要求的变截面钢板弹簧弯曲应力计算分析模型,利用此模型可精确获得钢板弹簧任意点的应力与簧片结构参数、应力与载荷之间的对应关系。
(3)利用P-S-N曲线进行疲劳分析,得到钢板弹簧等寿命图,获取在给定载荷工况下的簧片循环次数,相关结论可为台架试验提供理论基础。
