基于稀疏响应面的麦弗逊悬架多约束优化

李 璞，李 澄，黄长征，王洪荣，胡松喜

（1.韶关学院 物理与机电工程学院，广东，韶关 512005；2.中国汽车工程研究院，重庆 401122）

车辆操控性能主要受车辆悬架系统运动特性的影响，由于悬架系统的硬点位置在很大程度上决定其运动特性，所以这些硬点位置的坐标通常被定义为悬架系统运动特性优化的设计变量。

麦弗逊悬架具有结构简单紧凑，簧下质量小，占用车辆空间少等优点，在现代汽车特别是前悬架上应用极为广泛[1]。目前，对麦弗逊悬架的运动学分析通常采用空间机构运动学的数值计算方法和基于多刚体动力学软件的仿真分析方法[2]。由于悬架系统的复杂性，应用数值计算方法构建系统复杂且不够直观，悬架系统的模型通常使用机械系统自动动态分析（Auto Dynamic Analysis of Mechanical systems，ADAMs）等软件进行开发。但在模型的优化设计中，优化目标的计算需要频繁调用形如黑箱函数的软件模型，其计算仍较为费时。因此，响应面模型方法经常用于工程优化，以节省优化工作的计算成本[3-4]。

为构建精确的响应面模型，需要经过大量的采样，而多次采样需要多次调用黑箱模型，从而增加计算时间。利用源模型在某函数基上的稀疏性表示（即源模型可通过该组函数线性表示，且对应的系数大多为0），只需要通过少量的采样点，即可求解出非零系数[5]。因此，提出稀疏响应面方法，通过少量的采样点获得对麦弗逊悬架模型的精确逼近，基于稀疏响应面对悬架系统进行快速精确的运动学分析和参数优化。

1 麦弗逊悬架建模及运动学优化分析

1.1 ADAMs建模

采用ADAMs软件对某汽车的麦弗逊悬架建模，如图1所示。硬点参数的初始值见表1。

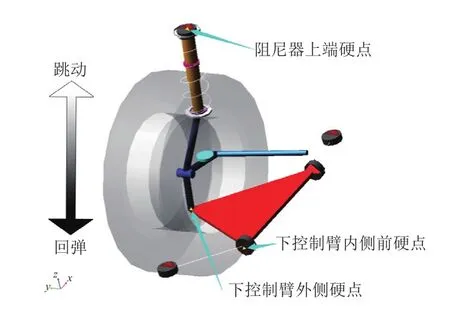
图1 麦弗逊悬架模型

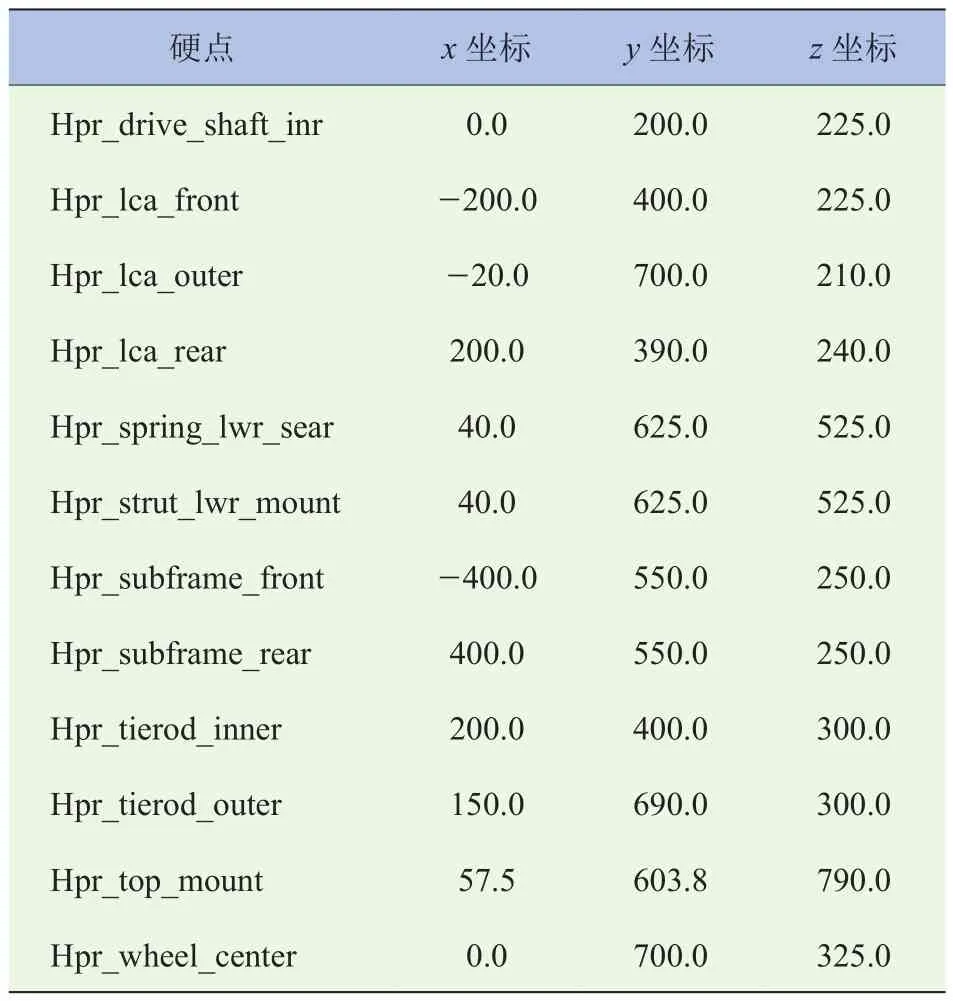
表1 麦弗逊悬架运动学参数初始值

1.2 优化目标

悬架运动学特征一般由主销后倾角、主销内倾角、车轮外倾角和前束角等参数描述。为获得运动学特性参数，在ADAMs/Car中对悬架模型进行双侧车轮同向跳动试验，跳动量设置为±对悬架模型，正号表示上跳，负号表示下跳。以此获得各参数在跳动试验中的结果，如图2所示。

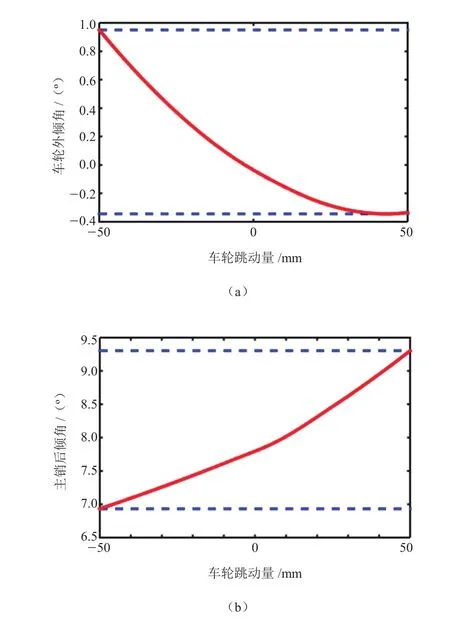
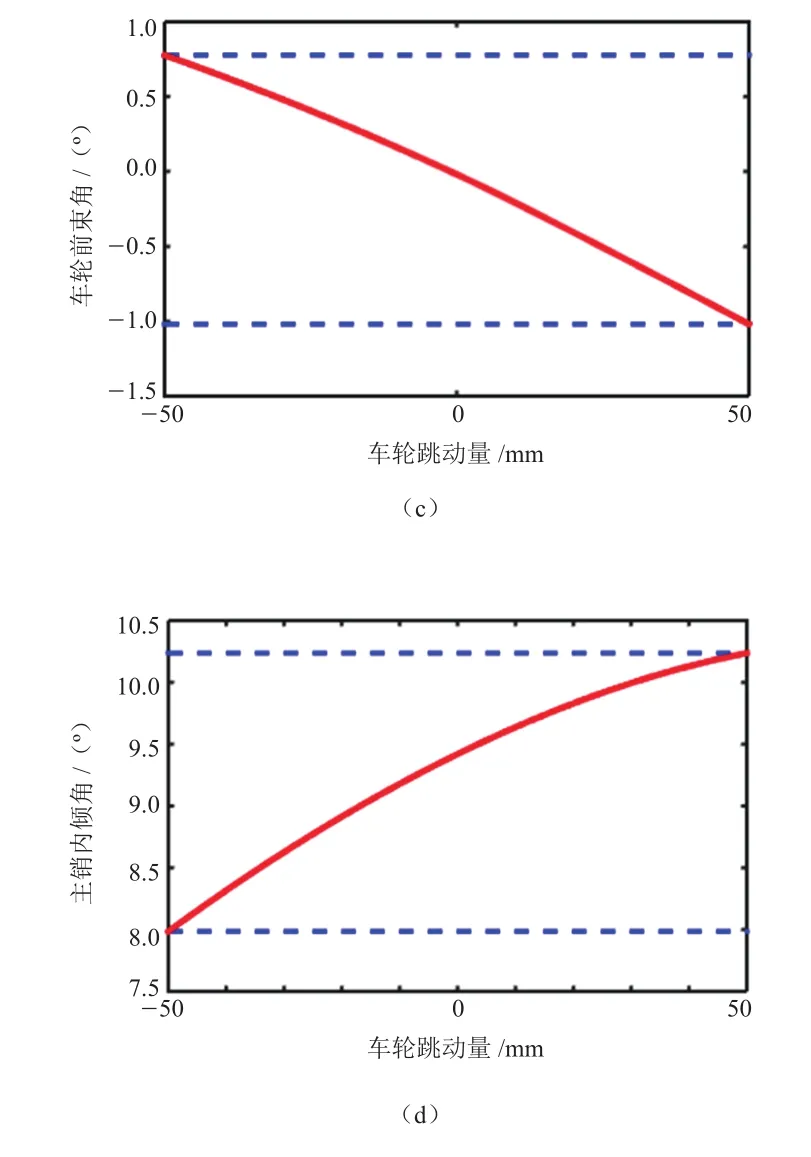
图2 各参数在跳动试验中的结果

为优化麦弗逊悬架的运动学性能，需要使以上参数在车轮跳动试验中变化最小，并约束车轮外倾角、主销后倾角和主销内倾角变化量分别不超过2°、2°和3°，约束前束角不小于-0.5°。该优化问题是一个多目标不等式约束优化问题，一般可通过多目标遗传算法求解[6]。为简化操作，通过设置权值将多目标优化问题转换为单目标优化问题。选择车轮外倾角、主销后倾角以及主销内倾角的变化量作为优化目标，通过给定权值转换为单目标优化问题。目标函数可表达为式（1）。

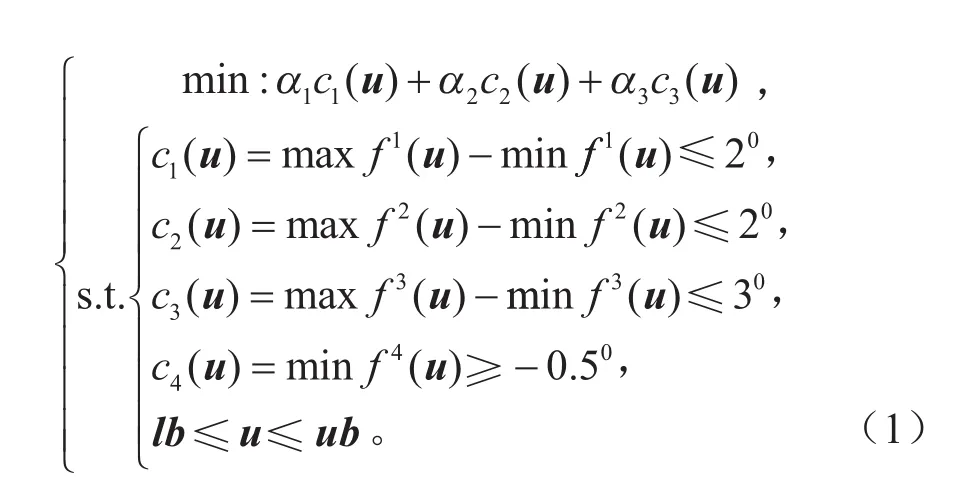
式中：u为包括设计变量的向量；lb和ub是设计变量的上下限；f1(u)、f2(u)、f3(u)、f4(u)为试验中的外倾角、主销后倾角、主销内倾角和前束角的取值，对应车轮外倾角、主销后倾角、主销内倾角的变化量；c4(u)为前束的最小值；α1、α2、α3为优化目标的权值，此处均选为1。

1.3 设计变量选择

为挑选出对优化目标影响较大的设计变量，对悬架模型的设计参数进行灵敏度分析，把灵敏度高的参数确定为设计变量。首先在ADAMs/Insight模块中以拉丁超立方设计（Latin Hypercube Design，LHD）的采样优化方法进行试验设计，选择出可能有影响的30个硬点参数，设置每个因子的变化量在-10～10 mm，进行32次迭代后取灵敏度最大的6个设计变量，分别为：下控制臂外侧硬点x坐标（lca_outer.x）、下控制臂外侧硬点y坐标（lca_outer.y）、下控制臂外侧硬点z坐标（lca_outer.z）、阻尼器上端硬点y坐标（top_mount.y）、阻尼器上端硬点z坐标（top_mount.z）、下控制臂内前侧硬点y坐标（lca_front.y），硬点位置详见图1标注。将所选6个设计变量分别命名为u1、u2、u3、u4、u5、u6，给定6个设计变量的设计空间为±30 mm，即可得：

2 稀疏响应面模型

2.1 稀疏响应面构建方法

2.1.1 稀疏响应面数学模型

稀疏响应面以多项式响应面为基础，可表示为线性模型：

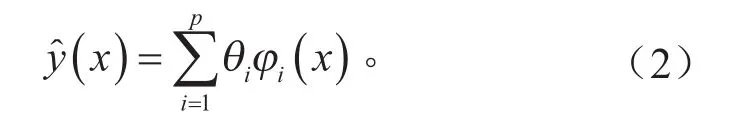
或矩阵形式：

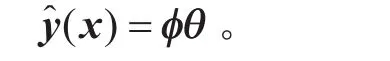
式中：x= [x1, …,xm]是一个设计采样点，m是响应面变量个数；{ϕi(x)}i=1,2,…,p是构成响应面的基函数，又称原子，p是原子个数；φθ是基函数集合，又称字典；是对应原子的系数；φθ是系数向量。选择一组Legendre多项式作为基函数，由于Legendre多项式结构简单易于构造，更重要的是在定义区间[-1,1]上关于l2范数正交，且该正交性的优点在由单变量扩展至多变量时能保留，所以Legendre多项式函数表达式通过循环定义获得：

设

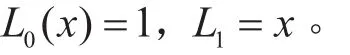
则

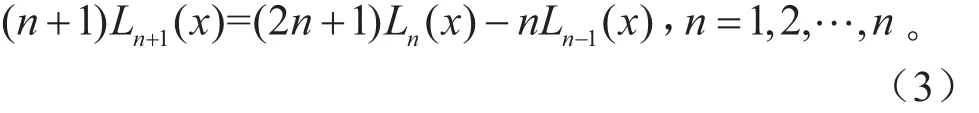
多变量响应面的基函数由单变量Legendre多项式的张量积构成。定义ϕi(x)为：

jjjjj

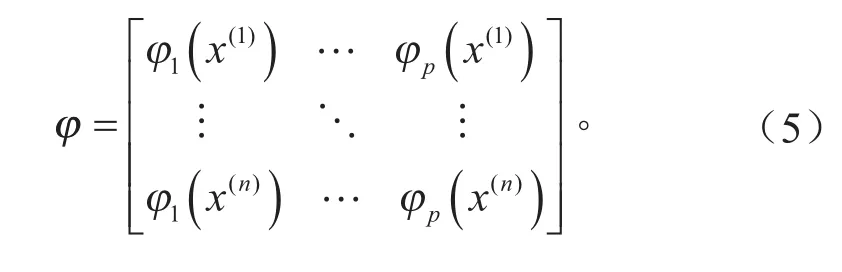
字典原子的个数需要权衡字典表达能力和求解的稳定性。字典的规模过小，不足以表达采样点所体现的模型特征和函数关系。相反，字典规模过大，系数求解方程会变成严重的欠定问题，求解稳定性变差。GRIBONVAL等[7]指出采样点个数n应至少是原子个数p的15%。在本模型中，取p= 6n。为避免过拟合并减少运算量，在选择Legendre多项式函数构造原子时优先选择低阶次的函数，即从0阶多项式往后选取。选择多变量模型的原子构造时亦遵循该准则，控制总阶次尽量小。

响应面采样位置的确定由LHD[8]获得。LHD采样将设计空间均匀划分成采样数量n个子区间，在每个子区间随机选取一个采样点，体现为均匀随机性。均匀性可保证采样到源模型的全局特征，随机性可以降低字典中原子的相关性，有利于分辨表达不同特征的原子。

可得到稀疏响应面模型为：

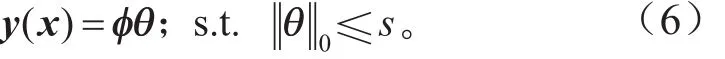
式中：s为稀疏响应面模型的稀疏度要求。

2.1.2 稀疏响应面模型求解

源模型在多项式基上的稀疏度是未知的，为构建稀疏的响应面模型，通过求解下式来获得基函数的系数：

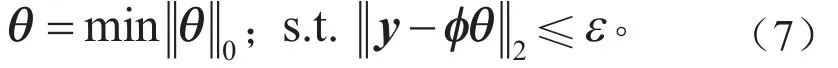
由于ℓ0范数问题是非凸的NP难问题，采用松弛方法，将其松弛到ℓ1范数：

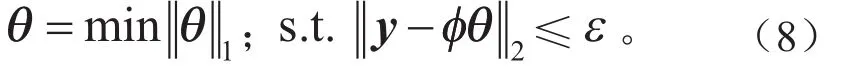
式（8）是可求解的凸优化问题，写成其拉格朗日乘子形式：

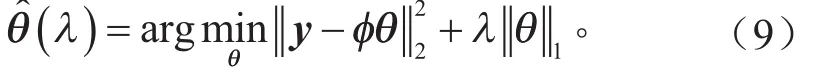
式（9）是最小绝对值收敛和选择算子、套索算法 （Least Absolute shrinkage and selection Operator，LAssO）回归模型。LAssO回归具有原子选择和系数收缩功能。变量选择可以生成稀疏的响应面模型，系数收缩通过牺牲模型训练精度提高了预测能力。LAssO提供稀疏模型的能力已经在统计学领域被证明。LAssO模型可以采用最小角回归[9]（Least Angle Regression，LAR）方法求解，并可借助Matlab的工具箱得到。稀疏响应面的构建流程见表2。

“研发这块我们还是挺给力的！”余保宁介绍，2018年，燕塘乳业设立了博士后科研工作站，成功通过国家优质乳工程验收。“全国仅有光明、三元、燕塘等十几家乳企通过了优质乳工程认证。这应该是目前全国最领先的一个标准，标志着我们国家真正从有奶喝到喝好奶！”

2.2 悬架运动学特性响应面

由式（1）可知，麦弗逊独立悬架的运动学特性优化是带有非线性约束的优化问题。采用稀疏响应面构建方法分别构建4个约束响应面由式（1）可知，目标函数由c1，c2，c3相加，所以不需要单独构建目标响应面，取对应的3个约束响应面的响应值的和即可。

表2 稀疏响应面构建流程

利用ADAMs/Insight模块在设计空间[lb,ub]内通过LHD生成60个采样点，进行双侧车轮同向跳动试验，输出7个目标值，即外倾角最大值，式（1）中maxf1(u)；外倾角最小值 ，式（1）中minf1(u)；主销后倾角最大值，式（1）中maxf2(u)；主销后倾角最小值，式（1）中minf2(u)；主销内倾角最大值，式（1）中maxf3(u)；主销内倾角最小值，式（1）中minf3(u)；前束角最小值，式（1）中minf4(u)，就可得到约束响应面的响应值。利用60个采样点的位置和对应的响应值，通过2.1节介绍的方法，可构建出约束响应面。

3 悬架运动学特性优化

3.1 优化方法

多变量非线性不等式约束优化问题通常可用内点法[10]、序列二次规划、信赖域法[11]、遗传算法[12]等方法求解。序列二次规划方法在处理中小规模问题时计算速度快、精度高，并可通过Matlab工具箱调用该模块工作。因此，本文选择序列二次规划方法对麦弗逊悬架运动学参数响应面进行优化。

整理式（1）的序列二次规划参数，见表3。

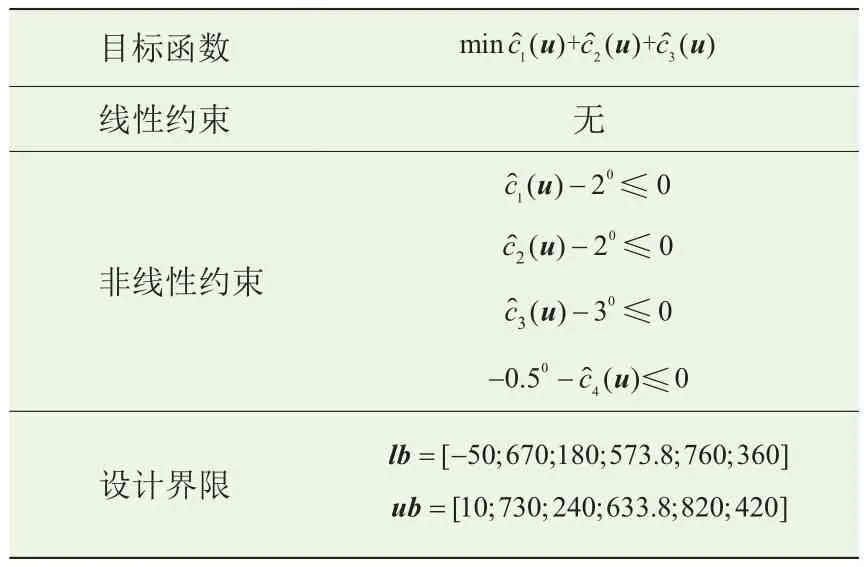
表3 麦弗逊悬架优化参数表

3.2 对比方法

为验证和比较所提出的稀疏响应面方法，选择了工程上常用的Kriging模型构建相同的约束响应面和目标响应面。

Kriging模型选择常数基函数和高斯关联模型，关联参数的初始值为θ0=1m×1，边界值为(i=1,… ,m)，其中m是变量个数，而1m×1表示元素全为1的向量。为使对比条件一致，构建约束Kriging模型和目标Kriging模型所用的采样点和稀疏响应面一致，所采用的优化也是通过调用Matlab软件的序列二次规划算法工具箱实现。

3.3 优化结果及分析

调用Matlab工具箱进行优化，分别将稀疏响应面模型和Kriging模型的最优解代入ADAMs/Car中进行仿真试验，得到优化前后各目标变量数值对比，见表4。

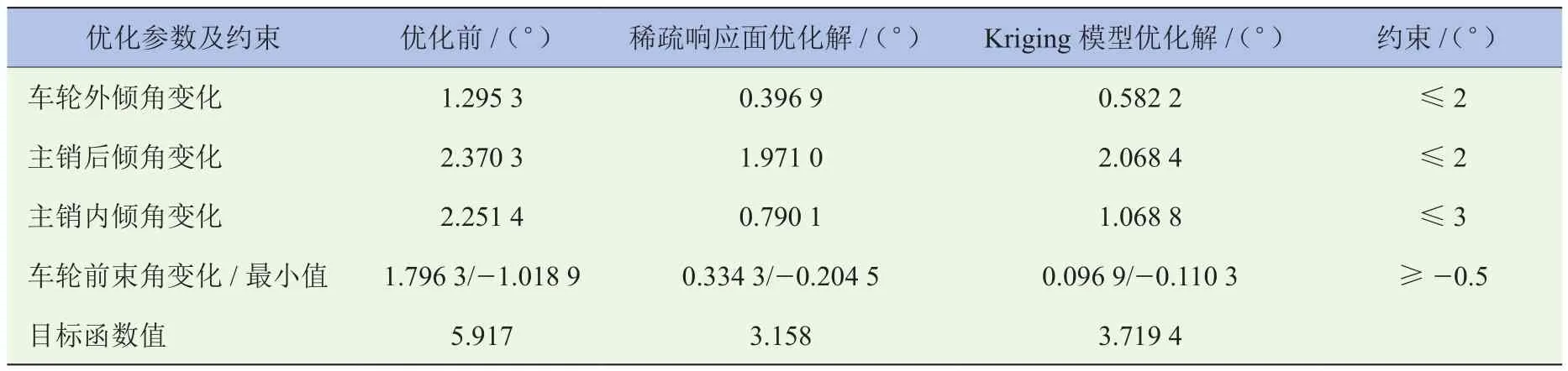
表4 目标变量优化前后数值对照表

由表4可知，基于稀疏响应面方法和Kriging模型优化出的结果均较优化前有明显提高。优化目标值由原来的5.917°分别降至3.158°（减少46.6%）和3.719 4°（减少37.1%），稀疏响应面方法优化的结果比Kriging模型优化的结果高了9.5个百分点。值得注意的是，基于稀疏响应面方法的优化结果各定位参数变换值均满足约束的要求，而基于Kriging模型优化的结果中主销后倾角的变化值为2.068 4°，超出了2°的约束，这是约束Kriging模型的精度不够导致的，而精度不够的原因主要是因为采样点过少。

该悬架原始参数和基于稀疏响应面优化后的参数在ADAMs/Car中仿真试验的对比曲线，如图3所示。

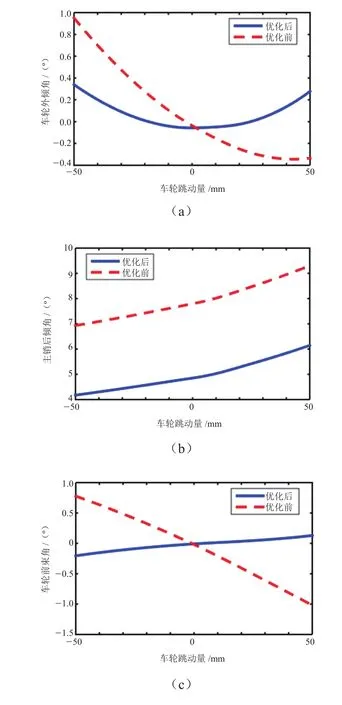
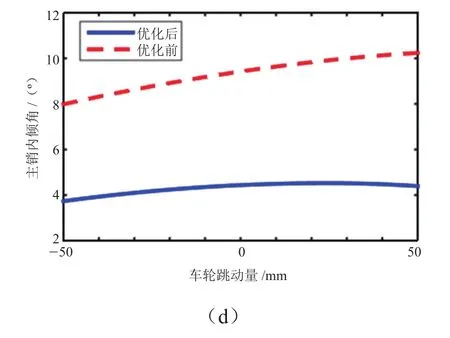
图3 各目标变量优化前后曲线对比

由表4可知，优化后的4个定位参数包括车轮外倾角、主销后倾角、主销内倾角以及车轮前束角的变化量都有明显减小。由图3可知，车轮外倾角、主销内倾角和车轮前束角的优化更加突出，特别是前束角的变化量，虽然没有被列为优化目标函数，但在优化过程中其值也有明显改善。

4 结论

本文提出了一种基于稀疏响应面和序列二次规划算法的麦弗逊悬架运动学性能优化方法。通过一组仅60个非自适应采样点，构建了4个6维的约束稀疏响应面和1个目标稀疏响应面。通过序列二次规划算法，基于所构建的稀疏响应面，对悬架进行了含非线性约束的优化。优化结果表明，目标函数值由5.917°优化至3.158°，减少了46.6%，且满足所有的约束要求。将所提出的稀疏响应面方法和工程上常用的Kriging模型方法进行了对比，基于Kriging模型的优化结果中，目标函数的函数值由5.917°优化至3. 7194°，仅减少37.1%，且主销后倾角不满足约束要求。由结果对比可知，本文所提出的方法较常用的Kriging模型优化法具有更高的精度，能够很好地解决工程中的非线性约束多目标优化问题。