基于电动汽车制动效能一致性的并联式制动能量回收控制

朱 波，张靖岩，张 农，尹 颖，刘 杰，饶淼涛

（1.合肥工业大学 汽车工程技术研究院，合肥 230000；2.北京新能源汽车股份有限公司，北京 100070）

制动能量回收系统可以将车辆制动过程中的部分动能转化为电能以提高能量利用率，增加续驶里程[1-2]。根据制动力分配模式的不同，制动能量回收系统主要分为串联式和并联式。串联式制动能量回收系统的特点在于机械制动力可根据电制动力矩大小而灵活调整，并联式制动能量回收系统（Parallel Regenerative Brake system，PRBs）在驱动轴上采用机械制动和再生制动联合制动，非驱动轴上仍采用传统的机械制动[3]，并且机械制动力部分不能灵活调整。串联式系统相对于并联式回收系统结构更为复杂，成本更高。由于国内在传统底盘动力学控制系统EsP/EHB电磁阀等关键零部件的设计和制造方面存在短板，国内各整车企业开发的纯电动乘用车大多不改变传统液压制动系统的结构形式，采用简单的并联式回收控制方式[4]。

李烨[5]分别从驾驶人、车辆设计、环境三方面指出了制动效能因素。谢文科等[6]提出了在一定制动强度范围内，保证制动舒适性前提下尽可能多地回收制动能的控制策略，但其对制动舒适性的评价仍采用主观标准。陈庆樟[7]设计了一种基于串联式回收系统的踏板行程模拟器，以保证再生制动过程中平稳的制动踏板感觉。刘杨等[8]定义了驾驶员驾驶解释一致性，即实际作用制动力与需求作用力之比。利用AMEsim与simulink联合仿真分别对串联式和并联式回收系统的回收效率和驾驶员驾驶解释一致性做了分析，结果表明，串联式系统回收效率和驾驶员驾驶解释性均优于并联式系统。李玉芳等[9]提出了电动汽车的制动踏板感觉一致性的概念，即相同的制动踏板输入必须对应产生相同的制动效能，但该概念只适用于串联式回收系统。

综合以上研究，对电-液复合制动感觉的研究目前还缺乏相应的客观评价标准，尤其缺乏与并联式制动能量回收系统特征相符合的评价标准。制动踏板感觉在驾驶员制动感觉中占有重要地位，因此，本文提出电动汽车制动效能一致性的概念，即驾驶员以不同制动踏板开度在不同初速度下进行制动，在采用电-液复合制动与只采取传统液压制动时，二者所得出的制动加速度和制动距离分布的差异情况，差异越小则电动汽车制动效能一致性越好。本文将提出一系列量化指标用于衡量制动效能一致性的优劣。由于再生制动力矩的引入，采用复合制动的电动汽车同时存在两种不同的制动力矩的来源。两者响应速度不同、作用地点不同、力矩传递路径不同、力矩响应特性不同。在制动安全性和制动舒适性方面，现有并联式回收策略分配的电制动力矩普遍偏低。这就造成了采用此种策略的并联式系统的能量回收效率偏低，不利于电动汽车整车经济性的提升。

针对以上几个问题，首先在AMEsim和simulink中建立制动系统模型和整车联合仿真模型；再分析现今主流并联式制动能量回收系统所采用的回收策略及其不足，提出基于制动效能一致性的能量回收控制策略；最后用联合仿真的形式验证回收策略对制动效能一致性的改善和能量回收效率的提高。

1 制动系统的建模

乘用车的制动系统主要包含制动踏板、真空助力器、制动主缸、制动管路、制动轮缸、制动器、轮胎和防抱死（ABs）系统等。

1.1 真空助力器模型

驾驶员踩下踏板，踏板力作用于真空助力器的推杆上。在输入踏板力达到最大助力点时，真空助力器在平衡状态下输入力与输出力有如下关系[10]：

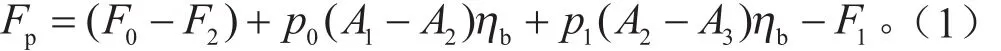
式中：Fp为真空助力器的输出作用力，即作用在制动主缸推杆上的力；F1为真空助力器膜片回位弹簧的作用力；F0为控制阀推杆的输入力；F2为真空助力器控制阀推杆弹簧的作用力；p0为真空助力器前腔和后腔的压力差；p1为前腔的最大真空度；A1为真空助力器膜片的有效面积；A2为真空助力器控制阀套管的截面积；A3为制动主缸推杆柄部的截面积；ηb为真空助力器的效率。

1.2 制动主缸和轮缸的数学模型

在此重点考虑的是液压缸输出力和负载力FL之间的关系，二者之间的关系可由式（2）表示[11]：

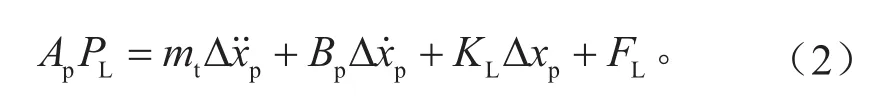
式中：Ap为液压缸活塞有效面积；PL为负载端压强，等式左边ApPL的乘积即为液压缸输出力；mt为活塞及负载折算到活塞上的总质量；Bp为活塞及负载粘性系数；KL为负载的弹簧刚度；∆xp为活塞偏离平衡位置的距离；FL为任意负载力。

1.3 制动管路压降

制动主缸的前腔室通过制动管路连接到左前轮和右前轮，后腔室通过制动管路连接到左后轮和右后轮，即II型管路布置方式。由于制动管壁并非光滑，以及液体本身在流动过程中存在粘性，所以存在一定程度的压力损失。在制动管路中的压力损失可参考式（3）[12-13]。

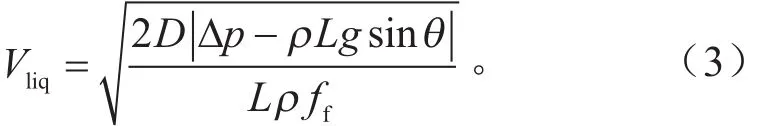
式中：Vliq为管路中的液体流速；D为管直径；Δp为压力损失；ρ为液体密度；g为重力加速度；L为管长度；θ为管道垂直于地面的坡度；ff为管壁摩擦因数。

1.4 单轮车辆模型

如图1所示，W为车轮受到的载荷力及自身重力，Fz为地面支持力，fμ为地面提供的摩擦力。对于传统制动系的车辆而言，根据车辆动力学方程可得：

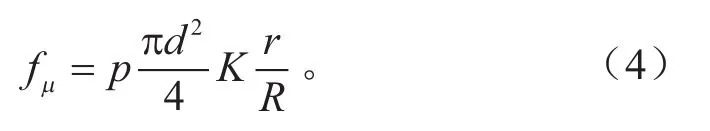
式中：p为轮缸输出压强；d为轮缸活塞直径；K为制动效能因数；r为制动器有效制动半径；R为车轮滚动半径。

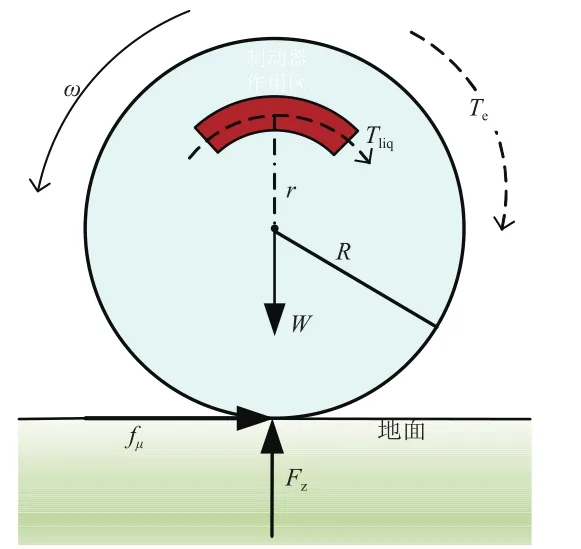
图1 单轮车辆模型

对于带有并联回收装置的制动系统而言，电机提供的再生制动转矩经过主减速器的放大，和差速器的均分（本文模型作用于前轴），驱动轮处的制动力为：

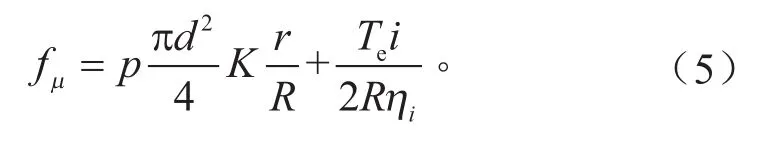
式中：Te为电机提供的制动转矩；i为主减速器比；Rηi为传动效率。

1.5 轮胎模型

纵向滑移率是衡量车轮抱死程度的一个重要指标，其计算方法如式（6）所示，其中V为车轮中心速度，即车速；ω为车轮转速。

如图2所示，纵向附着系数随着滑移率的增大，出现一个先增大后减小的过程，在20%附近达到峰值。

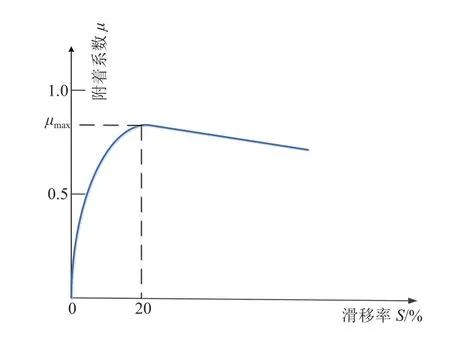
图2 滑移率-附着系数曲线

本文采用魔术轮胎模型，其力学表达式为[14-15]：

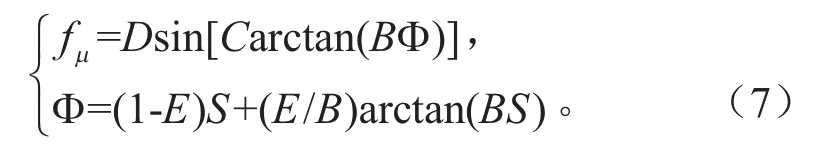
其中：

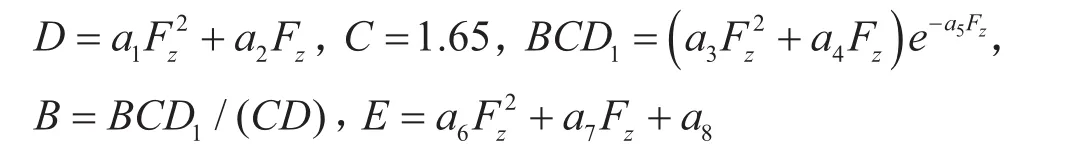
式中：D为峰值因子；C为形状因子；BCD1为纵向力为0时轮胎的纵向刚度；B为刚度因子；E为曲率因子；ai(i=1−8)为轮胎模型拟合系数。

1.6 ABs控制

紧急制动过程中要防止车轮抱死的情况出现，因此需要ABs系统。采用BANG-BANG控制策略来控制车辆滑移率，将滑移率控制在图2中的20%附近[16-18]。ABs控制器输入为实际滑移率与期望滑移率的逻辑判断，经过位开关控制，输出为制动盘制动力矩。设定两个逻辑门限值Smin和Smax。若滑移率小于Smin，则进入增压状态；若滑移率大于Smin而小于Smax则进入保压状态；若滑移率大于Smax则进入减压状态。控制策略流程如图3所示。

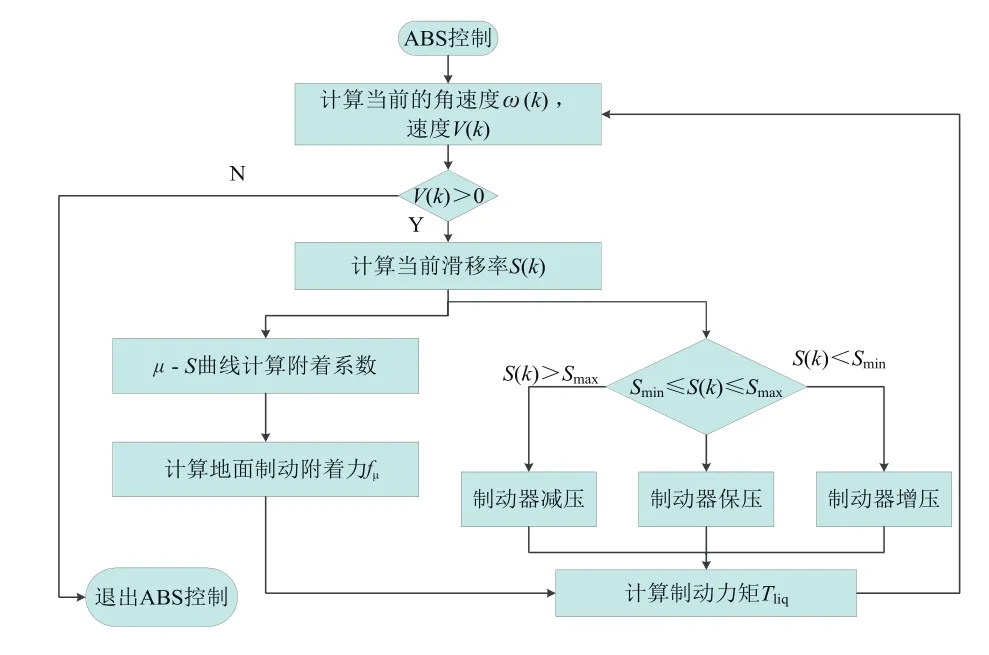
图3 ABs控制策略流程

1.7 AMEsim仿真实现

为了对制动系统进行相应的理论分析，建立了制动系统模型，采用西门子的AMEsim软件来进行制动系统建模。同时在simulink中搭建了VCU驱动和制动控制策略，进行联合仿真。

重点关注纵向制动效能一致性。AMEsim中搭建的模型如图4所示，构建模型的主要参数见表1。

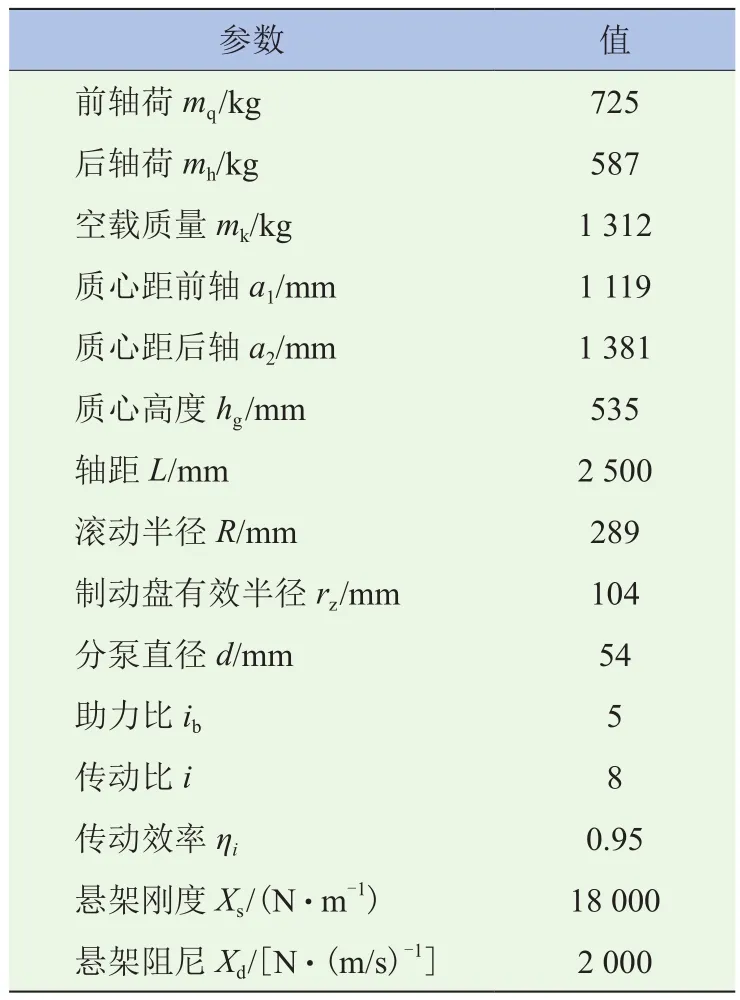
表1 模型参数

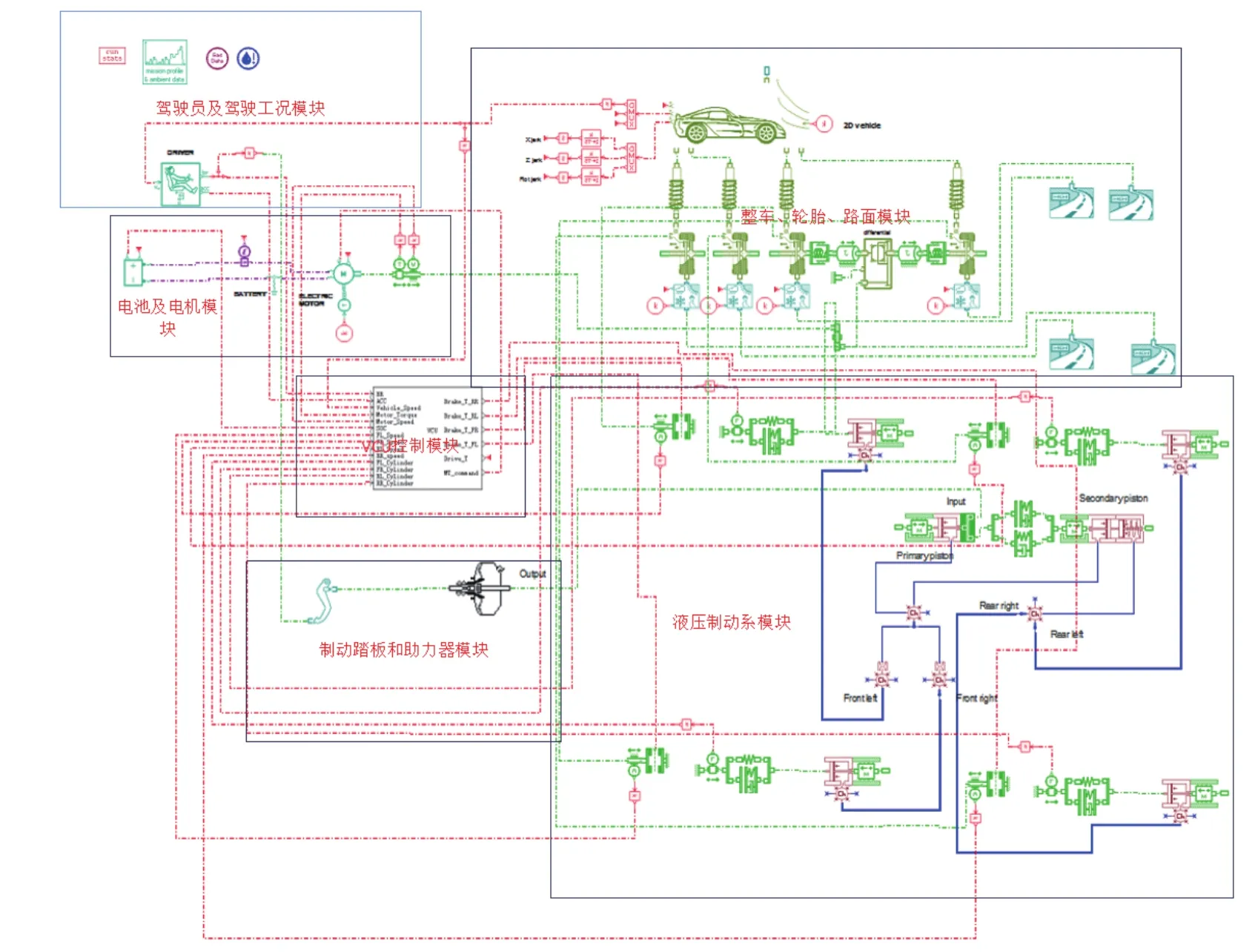
图4 AMEsim建模

2 传统制动系和PRBs的制动效能一致性分析

2.1 PRBs制动回收策略

如前文所述，电动汽车制动效能一致性是指在采用电-液复合制动与只采取传统液压制动时，二者所得出的制动加速度和制动距离分布的差异情况。这种差异主要从两个方面来衡量：一是从制动的动态过程角度，再生力矩的介入使制动加速度随着时间变化而变化的动态过程差异。二是从整个制动行为的输入输出结果而言，将驾驶员控制的制动踏板开度和采取制动措施时的制动初速度作为输入，整个制动过程所得到的制动加速度或者制动距离作为输出。因此，对一系列不同的输入量进行制动过程的仿真，从而得到一系列不同的输出量。对电-液复合制动的一系列输出量分布和传统制动系一系列输出量分布进行比较。

图5是目前常用的PRBs回收策略[19]，其控制原理为：一般PRBs没有制动踏板开度信号，而是采用制动灯开关信号来判断制动信号的有无。当检测到有制动信号时，则默认进入制动状态。进入该状态后，首先检测当前车速V是位于哪个区间。若V位于0-D区间，则再生制动转矩为0；若V位于D-E1区间，则再生制动转矩对应为D-E1斜线上0至深度回馈转矩值；若V位于E1-E2区间，则再生制动转矩恒定为深度回馈转矩值；若V位于E2-F区间，则再生制动转矩对应为E2-F斜线上深度回馈转矩值至0的值；若V＞F则再生制动转矩为0。

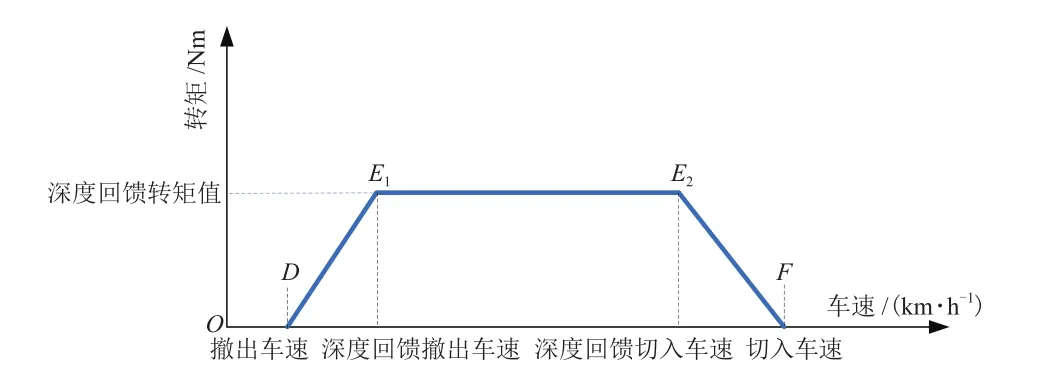
图5 常用PRBs回收策略

该策略按照固定的制动回收转矩曲线给电机回收命令，简单易行，但是存在制动回收率与制动舒适性的矛盾。深度回馈转矩设置过大，回收率较大，会引起制动加速度变化过大，影响乘坐舒适性；深度回馈转矩设置过小，制动舒适性较好，但制动回收率偏小，影响整车经济性。

同时，由于制动过程是一个减速过程，可能会出现车速从V＞F直至V＜D的情况，所对应的回收转矩也产生多次突变，造成制动加速度在制动过程中会产生几次突变，驾驶员很容易出现误判的情况，造成驾驶感觉的不平顺。

2.2 PRBs的动态制动过程分析

设置在峰值附着系数为1.0的路面上进行仿真，在制动效能一致性的标定中，采取的深度回馈转矩值为100 N，切入车速为100 km/h，深度回馈切入车速为90 km/h。深度回馈撤出车速为20 km/h，撤出车速为10 km/h。在19.8 s开始制动，制动初速度均为120 km/h。

图6～8的动态仿真结果分别是0.2，0.5，1.0三种不同的制动踏板开度下的制动加速度变化，代表着三种不同类型的制动工况，分别是小强度制动工况、中等强度制动工况和紧急制动工况。

在图6所代表的小强度制动工况下，由于PRBs的启动，电制动力矩造成了制动加速度的阶梯变化。制动强度本身较小，PRBs的启动和退出对制动过程影响最大。在图7所代表的中等强度制动工况下， PRBs的启动和退出同样也存在制动加速度的阶梯变化。在图8a所代表的紧急制动工况下，前轮已经接近地面所能提供的附着力极限，结合图8b和图8c可以看出液压制动转矩出现波动，ABs在PRBs启动时启动。PRBs启动和退出对制动加速度的影响已经不大。

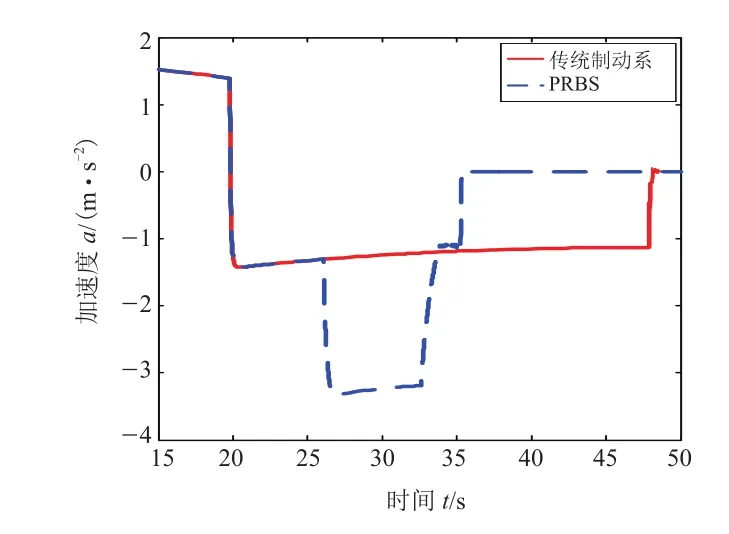
图6 0.2制动踏板开度下传统制动系与PRBs动态制动过程

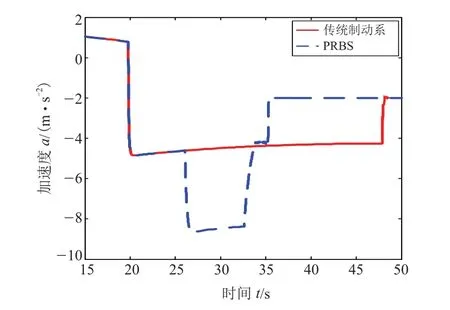
图7 0.5制动踏板开度下传统制动系与PRBs动态制动过程

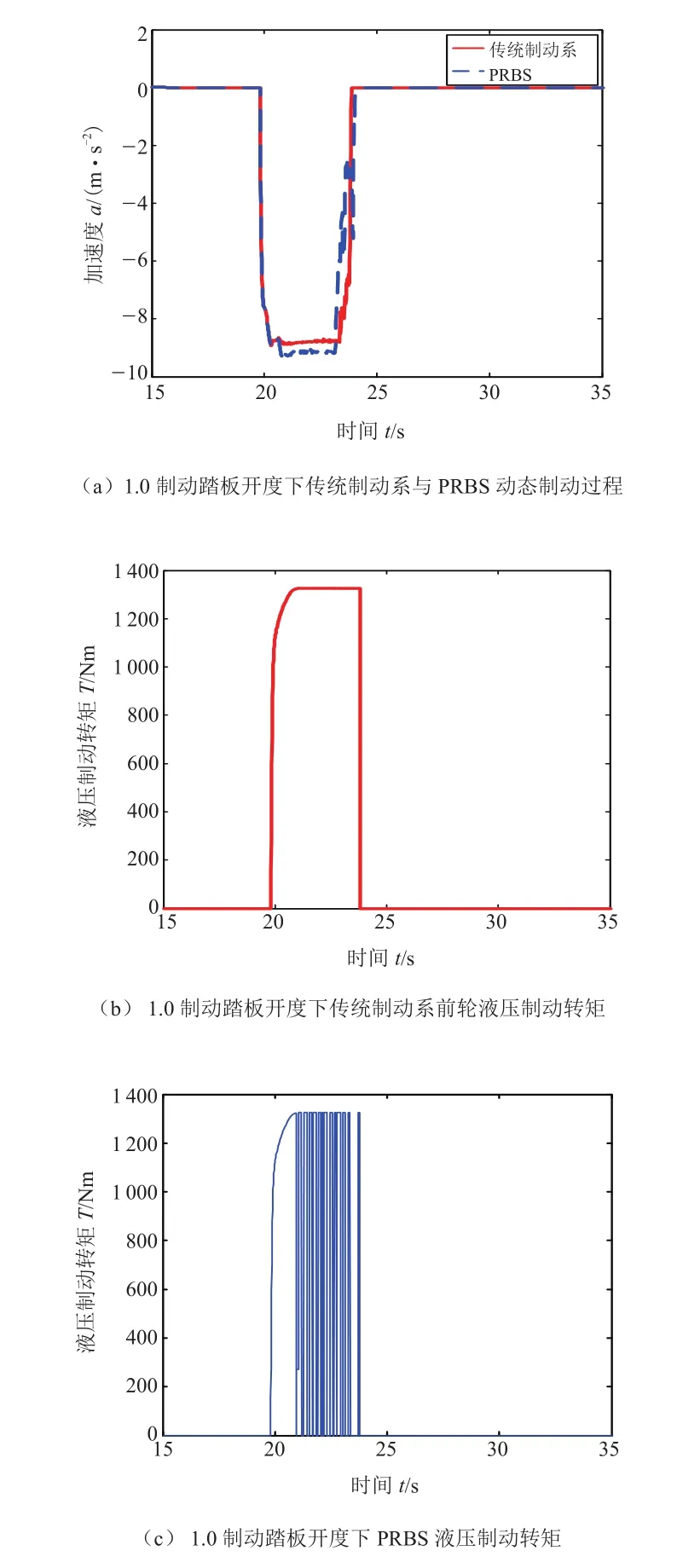
图8 1.0制动踏板开度下的制动加速度变化

表2 具体说明了PRBs的启动和退出对制动动态过程的影响，表中突变率的计算方法为：设abm为PRBs启动前最大瞬时制动加速度；aam为PRBs启动后最大瞬时制动加速度，则有

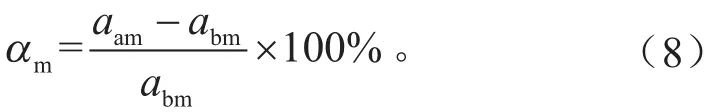
式中：αm为突变率。

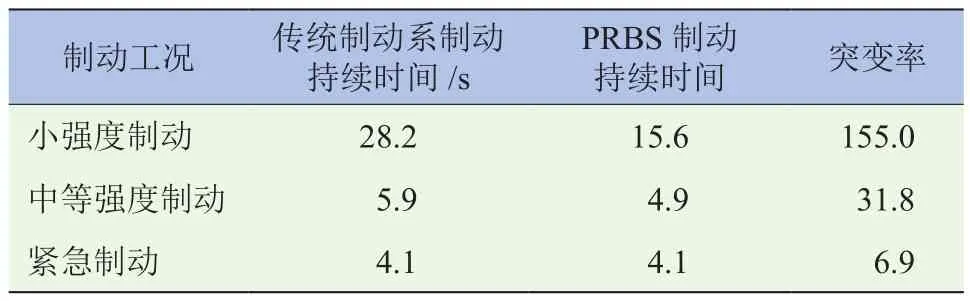
表2 制动过程动态仿真结果分析

可以看出制动强度越小，PRBs引起的制动加速度畸变越剧烈，所产生的制动感觉也与传统制动系差异越大。

3 基于制动效能一致性的能量回收系统

3.1 PRBs-BEC系统结构

为了减少PRBs与传统制动系之间制动效能一致性的差异，并改善制动的平滑性，本文提出PRBs-BEC。由式（4）可知，在传统制动系中，当制动强度小于路面附着系数，且ABs不介入时，制动加速度a与轮缸输出压力p成正比，而轮缸输出压力p大致与踏板开度λ成正比。因此，加速度a与制动踏板开度λ近似成正比。式（5）并联式回收系统中，等式右边第二项的电机再生转矩Te破坏了加速度a踏板开度λ的正比关系。若使电机再生转矩同样也与踏板开度成相同的正比关系，则会使并联式回收系统的制动效能一致性得到大幅改善。整个系统的结构组成如图9所示。

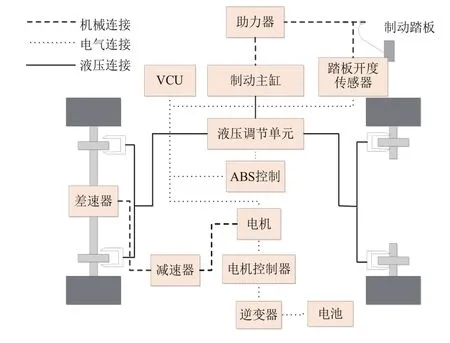
图9 PRBs-BEC系统结构

3.2 回收策略

由汽车理论知识可知，对于前后轴制动力按固定比例分配的车辆，保证β线在理想制动力I曲线下方，后轮不会抱死，属于稳定工况。I曲线的表达式为：

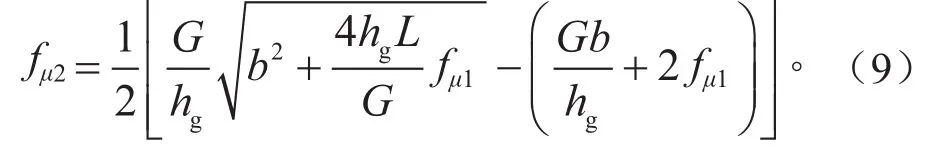
式中：fμ1为前轴制动力；fμ2为后轴制动力；G为整车质量；hg为车辆质心高度；b为质心距后轴距离；L为轴距。

本系统的制动力分配曲线为图10所示的折线段。OA段，制动踏板开度较小，同时，制动踏板处于空行程阶段，制动踏板未与液压系统产生机械连接，制动转矩全部由电机提供。AB段，由电机再生转矩和液压摩擦转矩协同制动，包含了回收制动转矩和液压制动转矩的前轴制动力与后轴液压制动力沿β线上升，同时满足在ECE法规最小后轴制动力分配曲线上方。

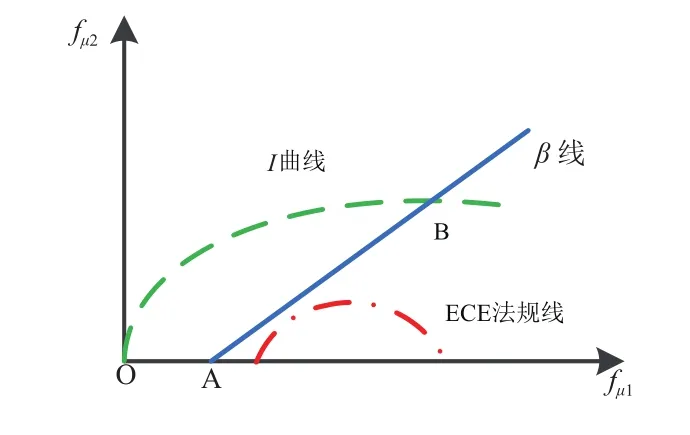
图10 前后轮制动力分配

定义如图11所示的电机最大回收曲线Tmax。

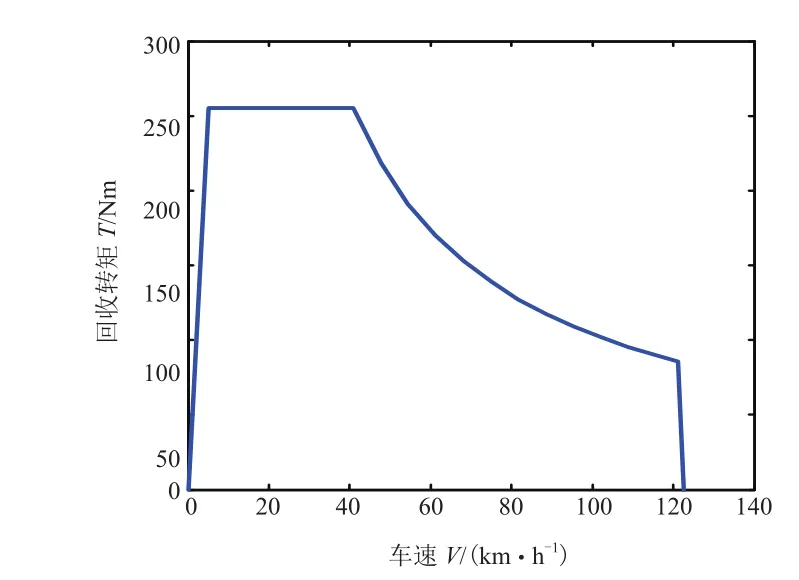
图11 电机最大回收曲线

为了使总制动力矩随制动踏板开度而成正比增加，如图12中的曲线1，在制动踏板开度小于λE时，制动踏板处于空行程，制动力矩全部由电机提供；大于λE时采用电机液压复合制动。

实际电机回收转矩Te由式（10）得到：

式中：Kλ为制动踏板开度修正系数。定义制动踏板开度向量代表制动踏板开度百分比；初速度向量(Vj= 1 0,2 0, … ,1 20)代表制动时初速度大小，km/h。

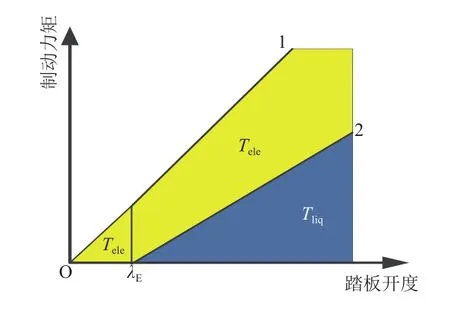
图12 再生转矩回收策略

常见制动效能指标是制动加速度a和制动距离J。这两个效能指标和制动踏板开度λ、制动初速度V密切相关。所以定义两个二元函数每个函数取108个样本点来估计其分布。

Kλ的标定主要考虑以下几个方面：

（1）制动加速度和制动踏板开度的线性相关度。线性度的大小主要由数理统计中的线性回归系数rl来确定。其计算方法如式（11）所示，其中别是样本中制动加速度和制动踏板开度的平均值。一般而言，线性相关系数越接近1，则线性变化趋势越明显。

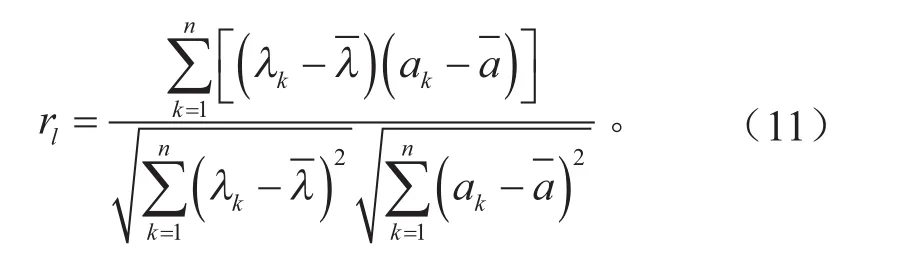
（2）同一制动踏板开度情况下，制动加速度随不同初速度的变化不宜过大。即二元函数偏导数小于某一个上限值A。

（3）能量回收效率不能低于上述提到的PRBs系统。

（4）满足图10所示的前后轮制动力分配关系，符合ECE法规。

具体的Kλ标定思路流程如图13所示。

4 仿真及测试结果

4.1 PRBs-BEC的制动效能对比分析

在AMEsim与simulink联合仿真环境下，对三种制动策略在不同的制动踏板开度和不同的制动初速度下进行多次仿真，结果图14所示。

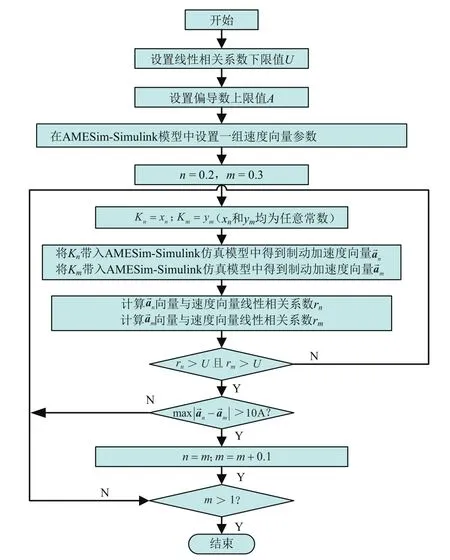
图13 Kλ标定思路流程图

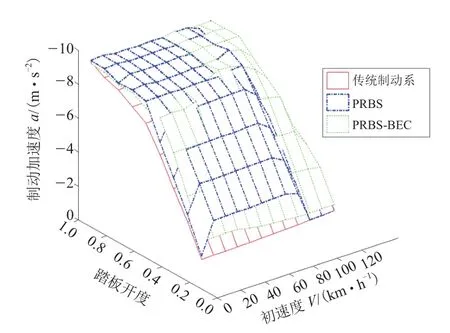
图14 三者制动加速度的分布

从图14中可以直观地看出PRBs函数平面“不平整”，存在两个比较陡峭的“斜坡”，即二元函数偏导数绝对值较大。当V等于某些特殊值（一般是车速处在切入车速和撤出车速时）时，偏导数绝对值存在过大的现象，会对驾驶员的制动感觉造成影响。PRBs-BEC函数平面和传统制动系函数平面较为平整。表3为的统计参数。最大值表征“函数平面的最大陡峭程度”，之和则表征“函数平面总体陡峭程度”。由表3可知，传统制动系无论是最大值还是之和都是最小的，表明传统制动系的制动效能发生畸变最少，函数平面最为“平整”，分布最为稳定，而PRBs-BEC的最大值以及之和介于传统制动系和普通的PRBs之间。表明PRBs-BEC相对于PEBs函数平面更为“平整”，产生的畸变较少，制动效能分布更为稳定。

其次，3个函数平面均存在“翻折现象”，但“翻折”的角度和出现“翻折”的位置均有不同。为了量化这种翻折程度的影响，表4列举了3种制动策略的线性回归参数。由表4可知，传统制动系的制动踏板与制动加速度的线性度最好线性相关系数rl为0.960，同时线性度波动幅度也是最小的；PRBs-BEC次之，线性相关系数rl为0.942；PRBs线性度最差，为0.916，线性度波动幅度也是最大的。这表明PRBs-BEC较PRBs更贴近于传统制动系的“简单-线性”制动感觉。

表3 三种制动策略的统计参数

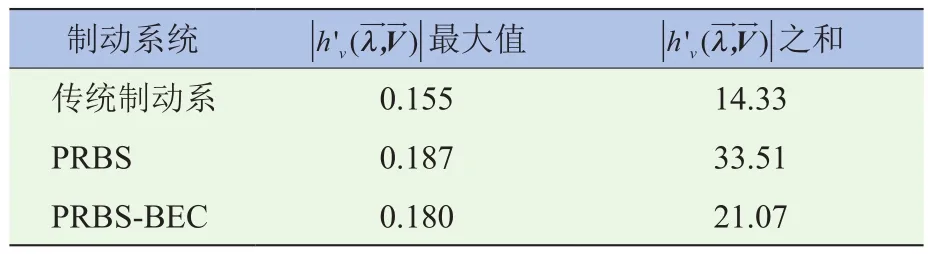
表3 三种制动策略的统计参数

之和传统制动系 0.155 14.33 PRBs 0.187 33.51 PRBs-BEC 0.180 21.07制动系统images/BZ_41_1625_1435_1733_1482.png■■■■最大值images/BZ_41_1975_1435_2083_1482.png■■■■

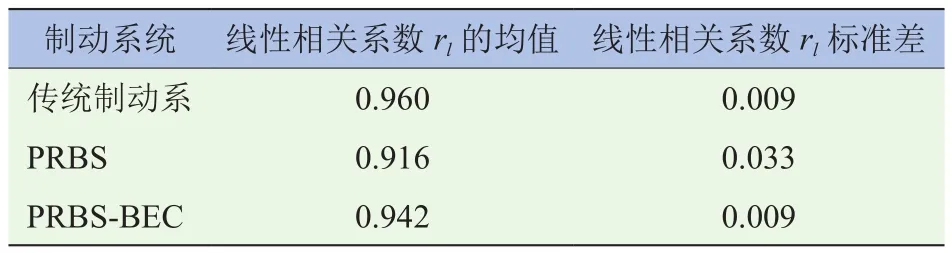
表4 三种制动策略的线性回归参数

图15为3种制动策略制动距离分布状况。由图可知，3种制动策略的制动距离分布变化趋势都是一致的，都是由左下方向右上方“上翘”的趋势。左下方由于制动强度大，地面所提供的制动力已接近地面附着能力极限，因此三者制动距离差距不大；右上方由于叠加在液压制动力基础之上的电机再生力矩的介入导致制动距离的减少。PRBs-BEC所代表的函数曲面更贴近于PRBs所代表的函数曲面。因此，从制动距离分布的角度而言，PRBs-BEC较PRBs更贴近于传统制动系。

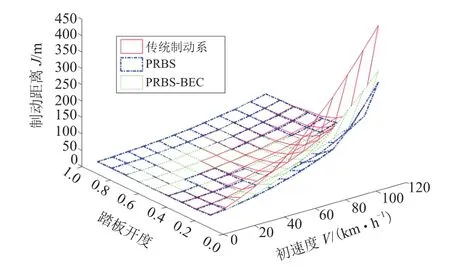
图15 三者制动距离分布

4.2 PRBs-BEC能量回收效率对比分析

设置电池初始sOC为50%，分别对传统制动系模型、PRBs和PRBs-BEC三者进行一个NEDC工况的仿真。表5是3种方案的能耗对比，图16为电池sOC变化情况。

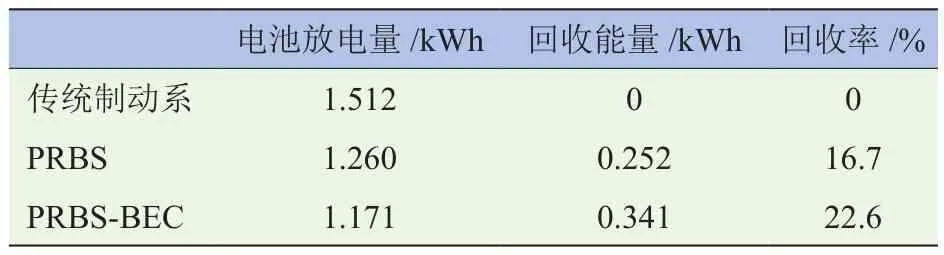
表5 三种方案能耗对比

图16中，传统制动系经过一个NEDC循环之后sOC变为43.6%，下降了6.4%；PRBs的sOC变为44.7%，下降了5.3%；PRBs-BEC的sOC变为45.0%，下降了5.0%。表4中PRBs电池总共放出1.260 kWh电量，回收了0.252 kWh电量，回收率定义为回收电量与电池放出电量百分数之比。PRBs的回收率为16.7%。PRBs-BEC电池放出电量为1.171 kWh，回收能量为0.341 kWh，回收率为22.6%。 PRBs-BEC回收效率较常用无制动踏板开度的PRBs高了5.9%。

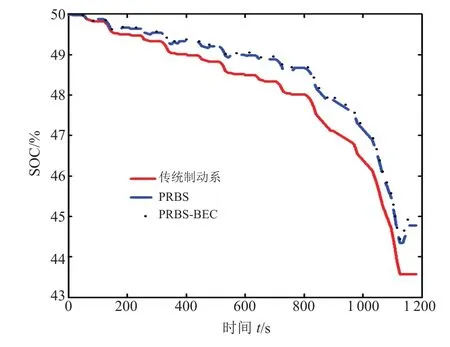
图16 NEDC工况下sOC变化情况

5 结论

（1）首先建立了并联式制动能量回收系统的模型，将制动系统与整车模型有机结合，对现有不考虑制动踏板开度因素的PRBs策略进行了分析，指出现有PRBs策略在制动过程中存在制动加速度突变的问题。

（2）通过引入制动踏板开度修正系数，提出了PRBs-BEC控制策略，PRBs-BEC策略较PRBs策略所产生的制动加速度畸变少，制动效能分布稳定。最大值以及之和均小于普通的PRBs。同时，PRBs-BEC制动踏板与制动加速度线性相关系数比PRBs更大。以上两点表明，PRBs-BEC的制动效能更接近传统制动系，在一定程度上改善了驾驶员的制动感觉。

（3）在改善制动效能一致性的情况下，PRBs-BEC策略较PRBs策略在NEDC工况下能量回收效率提升了5.9%。