CVaR准则下制造商服务的双渠道供应链定价研究
2019-04-04
(福州大学经济与管理学院 福建 福州 350000)
一、引言
随着信息技术的发展和互联网技术的日趋成熟与普及,电子商务活动在全世界范围内得以萌芽并蓬勃发展。可由于双渠道销售模式中的各方利益不协调冲突就演变得越来越明显,供应链的协调机制研究也从传统的单渠道扩展到双渠道,很多学者取得了一系列卓有成效的研究成果。
条件风险价值(Conditional Value- at- Risk,CVaR)方法不仅克服了均值方差和VaR方法的缺陷,还具有很好的计算性质。现实中,决策者在面临预期收益和损失时往往表现出风险厌恶的特性,因此,一些学者基于CVaR准则对供应链中某一决策层为风险厌恶时的订货量,定价和协调等相关问题进行了研究。闻卉等[1]研究了制造商和零售商均为风险厌恶者时供应链回购契约的优化和协调问题,徐兵等[2]建立了零售商为风险厌恶者时单制造商一两零售商供应链的集中式和分散式决策模型以及相应的协调合同。赵静和朱昆[3]考虑了包含一个风险厌恶的制造商和一个风险中性的零售商组成的双渠道供应链,运用博弈论和条件风险值(CVaR)准则,建立了3个博弈模型,即Nash博弈、制造商主导的Stacklberg博弈和零售商主导的Stacklberg博弈模型。
基于服务的重要性,肖剑等研究了制造商把线上服务交给线下渠道完成的情况,探讨了制造商和零售商线上渠道边际服务成本对销售定价与需求的影响。张盼运用Hotelling模型,研究了线上渠道的增加对零售商销售价格、提供的服务水平及其获利的影响,并讨论了消费者存在信息搭便车行为时零售商是否开通线上直销渠道的博弈均衡。研究结果指出,零售商都开设线上直销渠道是一个囚徒困境。
然而,各方利益博弈已经由传统的产品竞争延伸到其它方面,尤其表现在服务水平的竞争上,产品制造商高质量的服务能实现客户忠诚和提升企业业绩。因此,存在定价、服务和订购量联合决策的问题。考虑参与者风险厌恶,制造商提供服务的双渠道供应链协调机制就成了许多制造企业亟需解决的问题。
二、问题描述及假设
本文考虑包含一个风险中性制造商和一个风险厌恶零售商的两级双渠道供应链模型,制造商开通双渠道将产品售卖给终端顾客。制造商为了得到顾客的青睐,向顾客提供专业化技术和售后服务。随着服务水平的提高,花费的成本将更多。但是通过服务能使顾客的忠诚度增加,市场需求也会相应增加。
为了便于分析,对参数符号进行说明:
r或d—直销渠道或电子渠道;Dr或Dd—直销渠道的市场需求或电子渠道的市场需求;a—潜在的总市场规模;a0—稳定不变的总市场需求,a=a0+ξ;θ和1-θ—传统零售渠道和电子直销渠道所占的市场比例;ξ—市场需求变化部分的随机变量;p—一致性定价策略下的销售价格;w—制造商的批发价,是一个外生变量;c—制造商的单位生产成本;qr—零售商在销售初期的产品订购量;qd—制造商的为应对市场需求的产品期初存货;αi—自身渠道的价格对市场需求的敏感系数(i=r或d);βi—两渠道的交叉价格敏感系数;δi—制造商服务水平对渠道边际需求的敏感系数;φi—销售价格对市场需求的敏感系数;m—制造商服务成本的敏感系数,不失一般性,m≥2。根据上面说明,产品通过直销渠道和零售渠道售卖时需求函数分别是:
Dr=θa-α1pr+β1pd+δ1vDd=(1-θ)a-α2pd+β2pr+δ2v
其中,a表示潜在的市场规模,由于市场需求是随机不确定的,ξ是一个随机变量,服从均匀分布,即ξ~U(-u,u),它的累积分布函数和概率密度函数分别为F(x)和f(x)。
本文采用一致性定价策略pr=pd=p。制造商决定产品的价格p和直销渠道的生产量qd,零售商决定向制造商订货的订购量qr。本文假设未销售完的产品的残值为零,对于生产和销售不足没有短缺惩罚或造成的信誉损失。其中制造商的批发价格w在决策之前事先给定,是外生变量,零售商知道具体的批发价格。根据以上的假设和分析,为了简化计算,可以令c=0。那么得到零售商和制造商的需求函数分别是:
Dr=θ(a0+ξ)-φ1p+δ1vDd=(1-θ)(a0+ξ)-φ2p+δ2v
三、分散决策模式下的定价策略
在开始分析之前,我们先来了解CVaR的相关概念。CVaR度量了低于η分位数的收益的平均值,忽略收益超出分位数的部分,这往往是决策者所关心的。其具体定义如下:
(1)
其中,E表示目标函数的期望值,η∈(0,1]表示决策者的风险规避度(risk-aversion),η越小,表示决策者越害怕风险,也就越是风险规避型的。π(x,y)表示确定性变量x和随机变量y下的收益函数;g(y)为y的密度函数;qη(y)表示随机变量y的η分位数,即:
qη(y)=sup{v|Pr{π(x,y)≤v}≤η}
(2)
关于CVaR有一个更一般化的定义,可以表示为:
(3)
Rockafellar和Uryasev证明了上述两个定义在广义条件下是等价的,不过式(3)相比于式(1)它更便于数学计算和分析,所以一般更倾向于采用后者来建立目标决策函数。
本文考虑零售商为风险厌恶而制造商为风险中性的情形,可以得到零售商在CVaR下的利润函数表达式为:

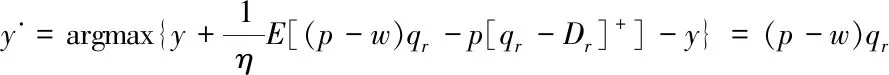
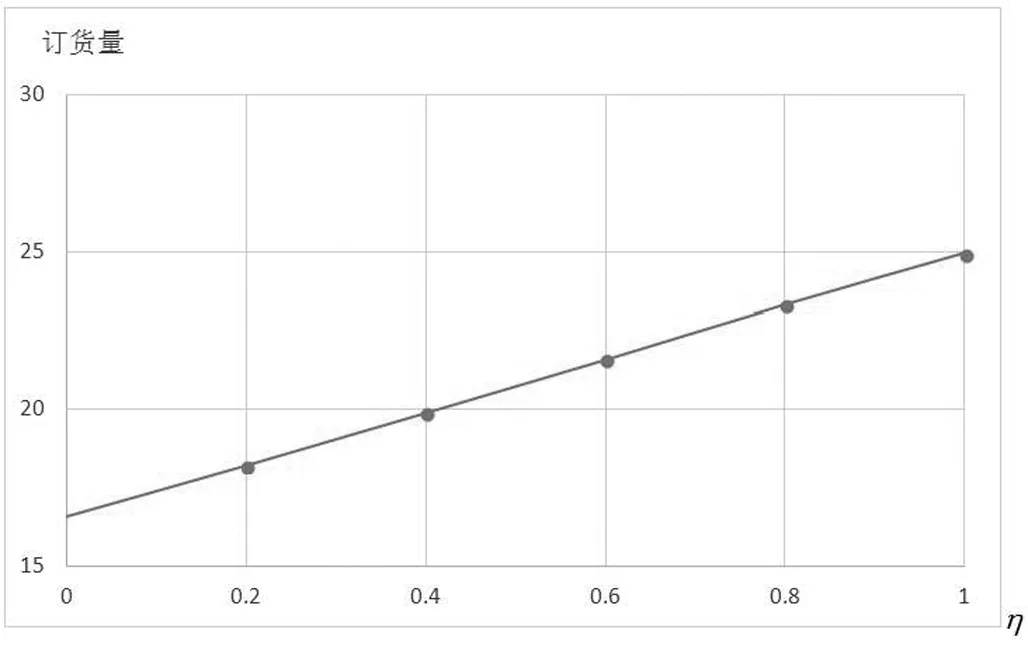
(2)当0<(p-w)qr-y (3)当(p-w)qr-y≥p[qr-Dr]+时,零售商的利润函数为 =max{y}=(p-w)qr-p[qr-Dr]+ 又因为它是连续的,因此可以得到 通过上面的分析,制造商和零售商的利润函数分别如下所示: (4) (5) (6) 将其代入制造商的利润函数中,再用利润函数分别对销售价和生产量求偏导,有 根据上面的方程组解得: 2φ2p*3+(φ1w-δ2v-(1-θ)a0)p*2-2uηθw2= 0 (7) (8) 命题(1)对于给定的其它参数,销售价格p*随着制造商服务水平v的增大而增大。 命题(1)至(3)表明不仅零售商的最优决策与制造商服务水平v有关,而且制造商的最优决策也与服务水平v有关。命题(1)表明尽管价格由制造商确定,会受到制造商服务水平的影响,随着服务水平的增大,价格也会增大。当服务水平增大时,制造商的服务成本也会增加,且增加的幅度更大,因此制造商通过提高价格来使其受益。命题(2)表明制造商的产品生产量也会随着服务水平的提高而增大,由于制造商提供服务且服务水平提高,所需的服务成本会相应的提高,为了能使收益最大化,在价格增大的同时来提升产量使收入增大。命题(3)进一步分析了零售商的订货量与制造商服务水平之间的关系,我们发现随着服务水平的增大,零售商的订货量也会增大。 (9) 解得最优解的表达式为 (10) (11) (12) 由式(10)可知价格p是一元三次方程,最优解存在,根据盛金公式得 证明:盛金公式,可以得出价格的解。 命题(4)对于给定的参数,产品价格随着风险规避度η的增大而增大。 (13) 制造商的服务水平v随着风险规避度η的增大而增大。 命题(6)对于给定的参数,制造商的产品生产量qd随着风险规避度η的增大而减小。 证明:由式(12)可得制造商的产品生产量是关于价格的函数,即 命题(7) 1)当(1-θ)a0-2φ1w≥0时,零售商订货量随着风险规避度η的增大而增大;2)当(1-θ)a0-2φ1w<0时,零售商订货量随着风险规避度η的增大先减小后增大。 命题(4)到(7)表明不仅零售商的最优决策与风险厌恶系数η有关,而且制造商的最优决策也与零售商的风险规避度有关。命题(4)表明尽管价格由制造商确定,但是仍然受到零售商风险规避度的影响,随着风险厌恶的增大,价格也会增大。命题(5)证明了制造商的服务水平随着零售商风险厌恶系数的增大而增大,表明当零售商越是风险中性的,价格会提高。命题(6)表明了制造商的产品生产量与零售商风险厌恶的关系,制造商生产量随着风险厌恶系数的增大而减小。命题(7)进一步分析了零售商的订货量与自身风险规避度之间的关系,我们发现当(1-θ)a0-2φ1w≥0时,零售商的订货量随着η增大而增大;当(1-θ)a0-2φ1w<0时,若p**∈(0,p0),零售商的订货量随着η增大而减小;若p**∈(p0,+∞),零售商的订货量随着η增大而增大。 为了比较集中决策和分散决策模式下供应链的利润,我们接下来在这一小节考虑集中决策模式下双渠道供应链的利润和决策变量。那么在集中决策模式下整个供应链的利润函数表达式为: πsc=maxπm+CVaRη(πr) (14) 通过上文的分析,可以得到集中决策模式下整个供应链的利润为: 零售商的订货量随自身风险厌恶度变化的情况比较复杂,考虑以下两种情况:1)a0=100,w=15,u=20,φ1=0.6,φ2=0.8,δ1=0.4,δ2=0.6,θ=0.4,m=2;2)a0=100,w=25,u=20,φ1=0.8,φ2=0.6,δ1=0.6,δ2=0.6,θ=0.7,m=2。 图一 零售商风险厌恶水平对订货量的影响 图二 零售商风险厌恶水平对订货量的影响 情况1)如图一所示,当(1-θ)a0-2φ1w≥0时,零售商订货量随着η的增大而增大。由于价格增大,批发价不高,理性的零售商会通过提高订货量来最大化自身利润。情况2)如图二所示,当(1-θ)a0-2φ1w<0时,零售商订货量随着η的增大先减小后增大。这种情况表明零售商订货量并不是与η成线性关系,这与定理(7)所描述的情况一致。存在p0=22.29,当p**∈(0,p0),零售商订货量随着η的增大而减小,当p**>p0,零售商订货量随着η的增大而增大,即η=0.49是一个极值点。 在这一小节我们设计一个新的契约,基于传统收益共享契约的改进,考虑到零售商的风险态度和制造商的服务成本对供应链的影响,我们结合回购和成本共担契约,将这个契约称为改进型回购契约(b,k)。其中b为制造商的回购价格,k为零售商成本共担比例。下标ib表示改进型的契约(improved buyback contract)在此情况下制造商和零售商的利润函数表达式分别是: 根据零售商的反应函数可以得到零售商订货量的反应函数为: 通过求解可得,为了使供应链得到协调,当w=bib时,该契约下的零售商订货量与集中决策下的零售商订货量相等,将w=bib带入上面的一阶条件得销售价格和服务水平的反应函数为:δ2pib+2δ1bib-(1-k)mvib=0。集中决策模式下销售价格和服务水平满足(δ1+δ2)psc-mvsc=0,为了使pib=psc,vib=vsc,所以 为了使b>0,通过分析得出传统零售渠道所占的市场比例θ满足: 为了使0 以上分析表明,当λ1<θ<λ2时,基于回购和成本共担的契约能够实现供应链的协调,这就要求零售商的传统销售渠道市场比例不能偏大也不能偏小。当零售商的市场比例较小时,它不会愿意为零售商承担服务成本,这样做显然会使自身的利润急剧缩小,甚至入不敷出。当零售商的传统销售渠道市场比例较大时,制造商的回购价b<0,相当于零售商的收益共享契约,这种情况下供应链无法得到协调。当w=b时,相当于制造商承担了零售商的风险成本,鼓励零售商根据自身实际的市场份额来确定最优的订货量。作为回报,零售商为此承担了一定比例的服务成本。 本文运用CVaR方法分析了双渠道销售模式下提供服务的风险中性制造商和风险厌恶零售商的定价与协调问题。得到集中决策和分散决策时的均衡解析解,分析了集中和分散决策下服务水平对价格和需求的影响。研究显示,不论是集中决策还是分散决策,制造商服务水平的提高都会导致两个渠道销售价格提高。同时,分散决策模式下服务水平的提高还会促进两个渠道销量的增加;而在集中决策下,整个供应链的利润随着服务水平的提高先增大后减小,在服务水平达到某一特定值时取得最大。我们发现分散决策下,随着零售商越趋向于风险厌恶,销售价格和服务水平将会越小,而制造商的产品生产量会增大;而零售商的订货量与自身风险厌恶因子的关系会因为参数的取值不同而有所不同。集中决策模式下,整个供应链的利润随着零售商风险厌恶因子η的增大而增大。我们发现基于零售商收益共享和制造商风险共担的契约无法实现双渠道供应链的协调。在基本的收入共享和成本分担策略对供应链协调机理失调进行分析的基础上,根据制造商的服务水平,设计出了基于回购和成本共担的契约,并进一步研究了为实现系统改进的成本共担因子满足的条件,并给出一些有意义的结论。 双渠道供应链的定价与协调问题的研究,所需要分析和论证的新问题有很多。基于本文的研究,依然有几个方面值得深入挖掘和拓展。首先,本文考虑的是零售商为风险厌恶型的,而制造商和零售商均为风险厌恶的情形是值得研究的问题。第二,本文考虑的是两级供应链系统,然而随着信息技术的日新月异和电子商务的深化发展,整条供应链上多个零售商开通电子渠道的销售模式也将导致渠道间竞争和合作问题的出现,对于多级供应链的协调问题将是新的研究方向。
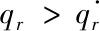
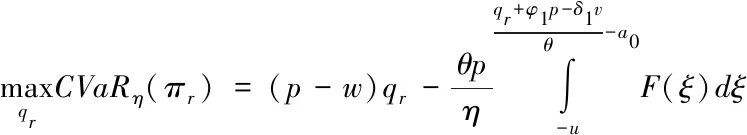
(一)渠道成员决策随服务水平变化的策略分析
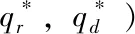
(二)渠道成员决策随η变化的策略分析





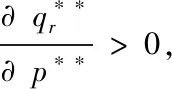
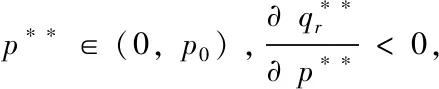
四、集中决策模式下的定价策略

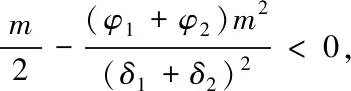
五、数值分析

六、双渠道供应链的协调
(一)基于回购和成本共担的契约分析
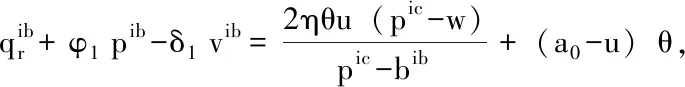
七、结论与展望
