试析高中数学解三角形的授课技巧

黄文忠

(广东省陆丰市东海中学 516500)

高中时期数学课程的实际教学，解三角形是教学内容关键的组成部分.作为教师切实把握解三角形的授课技巧，既可以提升学生自身的解题能力，也能激发学生的数学思维能力.所以，一定要重视解三角形的授课技巧，综合教学改革中的有关要求，着重讲解正弦、余弦定理相关知识内容，使用有效的教学方式，让学生深入理解和把握解三角形的相关知识内容，深化学生对知识的记忆，实现教学目标.

一、重视对学生数学思维方式的培养

数学思维方式在实际教学中，属于高中数学课程的关键部分，有助于学生深化对解三角形相关知识内容的理解与把握.初中时期，学生都已经学习过有关边角关系的相关知识内容，在高中数学课程的实际教学中导入正弦定理相关知识的时候，可让学生基于已经学习过的几何知识，提出探究性意义的问题：在同一个三角形中，大边所对应的是大角，小边对应的是小角，这样的边角关联，那么，我们能不能知道这个边、角精准的关系呢？而在导入余弦定理相关知识内容的时候，可提出这样具有探究性意义的问题：倘若已知两个三角形的两条边和夹角对应相等，依据三角形的全等判定时，这两个三角形一定是全等三角形.基于量化的角度进行探究，探究怎样在已知的边、夹角的基础上探究三角形另一边以及两个夹角的相关问题，教师为学生设置这样的问题，目的是为了强化学生的数学思维方式.

二、高中数学解三角形实际教学中要着重讲解正、余弦定理

在高中时期数学课程解三角形的实际教学中，正、余弦定理相关知识是最为基础的定理内容，并且其也是连接三角形相关问题的有效方式.在高中教学改革的基础之上，为了满足解三角形教学的实际要求，在解三角形知识的实际教学中，着重讲解正、余弦定理知识是极为关键的.

1.正弦定理

教材内容中先引导学生对初中学习过的三角形有关内容进行回忆，引导学生学生将相关知识进行量化的表示，在实际教学中，作为数学教师，一定要理解正弦定理有关的知识内容，并且做好定理内容的外展阐释，让学生可以把握正弦定理独有的特点，学生解三角形过程中能够正确地使用正弦定理.所以，做好正弦定理知识的实际教学，对解三角形的实际教学来讲是极为关键的.

教学目标：经过对三角形边长以及角度之间关系的探究，把握正弦定理知识以及验证方式，会使用正弦定理来解决三角形基本问题.

教学方式：使用相关知识以及定理知识，对学生进行引导，让学生尝试观察、对比和推导，把握定理知识，并且能进行实践操作.

养成学生的探索精神，让学生具备数学思维能力，经过相关知识的关联来展示事物之间的辩证关联.

重难点知识内容：已知两条边与其中一条边的对角来解三角形相关问题.

例如，在图1中，在Rt△ABC中，假设BC=a，AC=b，AB=c，那么依据锐角三角函数当中的正弦函数定理，就能得到a/c=sinA，b/c=sinB，又因为sinC=1=c/c，所以a/sinA=b/sinB=c/sinC=c，因此在直角三角形ABC中，a/sinA=b/sinB=c/sinC.那么这个时候向学生提出问题：对于任意一个三角形来讲，以上的关系是否始终成立？这个时候让学生进行分析与讨论.

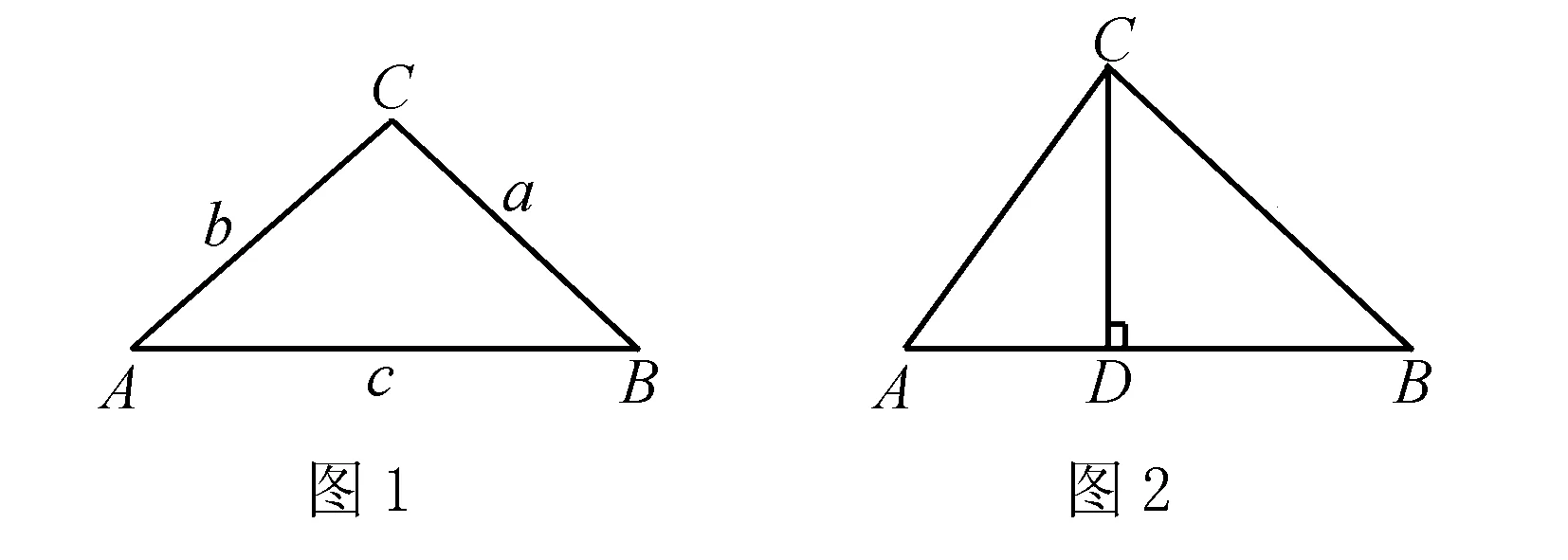
这个时候让学生进行探究思索：能否用别的方式来证明这个等式？

2.余弦定理

余弦定理，要探究三角形各边以及夹角之间的关系，并将其进行量化表示，探究怎样基于已知内容来推算另外边角的问题.正、余弦定理内容有些类似，是解三角形的重要定理，教师在余弦定理相关知识的实际教学中，一定要明晰正、余弦之间的差别，着手于现实，让学生学会使用余弦定理去解三角形，所以，做好正、余弦定理相关知识的实际教学，对于高中时期数学课程中解三角形知识的实际教学具有关键性作用.

教学目标：让学生把握余弦定理相关知识的表示形式以及验证方式，学会使用余弦定理知识解三角形基础问题.

教学方式：使用向量知识推导余弦定理，经过实践验算的方式，让学生掌握使用余弦定理相关知识解三角形基本问题.

养成学生基于方程思想内容的导向下，处理解三角形相关问题的能力；经过三角形、余弦定理相关知识内容间的关系，理解并掌握事物间辩证统一的关系.

重难点知识内容：勾股定理的发现以及验证过程.

总而言之，在高中数学课程解三角形相关知识的实际教学中，要重视对学生思维能力的有效培养，之后进行具体概念、解题方式的实际教学.为了让学生真正获得更为有效的提升，需要对学生的思维能力进行培养.学生只有掌握了思维方式之后，在使用具体有效的实践作业才能获得数学能力的真正提升.