浅谈《线性代数》中的实例教学

徐清华 赵清波 刘 烁 吴克坚 梁锐华

(空军军医大学基础医学院数理教研室 西安 710032)

线性代数是我校针对生物医学工程专业开设的一门重要基础课，它在很多学科比如计算机科学，生物学，通信，航空等领域中都有广泛的应用。生物医学工程专业是一门综合理学、医学和工学的交叉学科，因此线性代数在医工专业的后续课程，如电路，信号与系统，数字信号处理等课程中都有重要应用。

但是线性代数内容抽象，逻辑性强，很多学生并未体会到这门课程的价值和趣味所在，因此如何让学生了解这门课程在后续课程中的重要作用，从而提高学生的学习兴趣，是我们一直关注的一个问题。在多年的教学实践中，我们通过不断探索发现，只有结合实例的教学，才能让抽象的理论变得形象生动，才能激发学生的学习兴趣。因此，本文就实际教学过程中使用的一些案例做一些简单介绍。

1 向量组的线性相关性及药方配制问题

向量组的线性相关性是线性代数中最重要的内容，它是后续求解线性方程组的基础，更是矩阵的秩和方程组解的结构连接的纽带。这一节的内容理论性非常强，比如向量组的线性相关性的概念、最大线性无关组的定义、向量的线性表示等内容，扑面而来的大量定义、定理和术语，让学生感到非常困惑，无法理解，更不能在实际应用中灵活应用。

因此，如果在理论之后适当增加实例的教学，能减轻学生对理论知识的畏惧感，激发学生的学习兴趣，促进学生主动思考，培养学生理论联系实际的能力。因此结合学生专业特点，我们引入了中成药药方配制问题，来帮助学生理解向量组的线性相关性和向量的线性表示等知识。

中成药药方配制问题：某医院药剂科用九种中草药(A-I)，根据适当的比例配制成了7种特效药，各用量成份见表1。

表1 7种特效药用量成份表(单位:g)

中药1号药2号药3号药4号药5号药6号药7号药A10214122038100B1201225356055C531105140D79255154735E012255336F255355355550G94172523925H651610103510I821202620

(1)某药店要购买这7种特效药，但药剂科的第3号药和第6号药已经卖完，请问能否用其它特效药配制出这两种脱销的药品？

(2)现在药剂科想用这7种特效药配制3种新药，表2给出了3种新药的成份比例，请问是否能配制？如何配制？

表2 3种新药的成份比例

中药1号新药2号新药3号新药A4016288B6214167C14278D4410251E53607F5015580G7111838H416821I145230

(1)这类题目同学们首次接触比较困惑，但是仔细分析之后发现，如果把每一种特效药看成一个九维列向量，那么能否用其它特效药配制出第3号药和第6号药的问题，其实就是3号和6号这两个向量能否用其余向量线性表示的问题，所以问题转化为判断7个向量构成的向量组的线性相关性问题。如果向量组线性无关，那么无法配制需要的特效药; 如果向量组线性相关，并且能找到一个最大线性无关组，u3,u6能被这个最大无关组线性表示，则可以配制3号和6号药品。

由于数据量较大，若采用手工初等行变换计算较为麻烦，因此可采用数学软件Matlab进行计算，结果为：向量组线性相关，并且一个最大无关组为u1,u2,u4,u5,u7且u3=u1+2u2，u6=3u2+u4+u5，因此可以配置出这两种脱销的药品。

(2)有了第一问的基础， 第二问就比较简单了。3种新药用v1,v2,v3来表示，能否配制新的特效药的问题就转化为v1,v2,v3能否由7个向量u1,u2,u3,u4,u5,u6,u7线性表示的问题，若能表示，则可配制；否则，不能配制。

用Matlab计算可得：v1=u1+3u2+2u4，v2=3u1+4u2+2u4+u7，v3则不能被线性表示，所以可以配制1号和2号新药，3号新药则无法配制。

2 方程组求解及电路问题

在线性代数的教学中，方程组的求解贯穿始终，利用行列式计算的克拉默法则，利用初等变换计算的通解，利用基础解析写出的通解，对这些求解方程组的方法，很多同学都很容易掌握，拿到题目都能熟练的计算，但是一遇到实际问题就束手无策，原因就是理论联系实际能力太弱。

线性方程组应用非常广泛，很多实际问题的处理最后都归结为线性方程组的问题，比如在生物医学工程专业的后续课程中，大部分电路的问题都可以转化为方程组的问题来求解。

上图为电路网络图，设各节点的电流如图所示，要求出电路中各支路上的电流。由基尔霍夫第一定律可以列出方程：

对于节点A：i1+i4-i6=0;

对于节点B：i2+i4-i5=0;

对于节点C：i3+i6-i5=0;

对于节点D：i1+i3-i2=0;

于是求各个支路的电流就归结为下面齐次线性方程组的求解

解之，得其解为

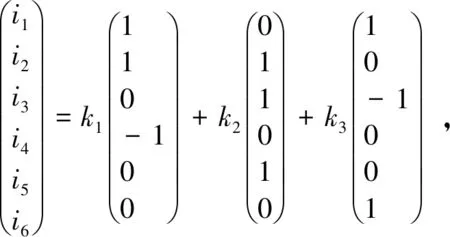
由于i1,i2,i3,i4,i5,i6均为正数，所以通解中的3个任意常数应满足以下条件：

k1<0,k2>k3>-k1

如果k1=-1,k2=3,k3=2，则：

i1=1,i2=2,i3=1,i4=1,i5=3,i6=2

3 矩阵的逆及加密通信问题

矩阵的逆在矩阵理论中占有非常重要的地位，也是一个较难理解的重点内容。很多学生能熟练计算矩阵的逆，利用逆矩阵求解矩阵方程，但是却不了解矩阵的逆在实际生活中的作用，对这部分的知识只停留在抽象的概念和机械的计算中。为了加深知识的应用及知识点的深刻理解，我们选取了同学们比较感兴趣的保密通信方面的一个问题来讲解。

加密技术在通信中有着重要的作用，加密的原理如下：发送方采用某种算法，也就是密钥，将明文数据加密转化成密文数据后发送给接受方，接收方则可以采用对应的某种算法将密文数据解密转换成明文数据。从矩阵的角度来解释就是，明文用矩阵X来表示，加密密钥为矩阵A，则加密过程就是矩阵方程AX=C，密文是矩阵C，解密密钥为矩阵B，解密的过程为X=BC，加密技术是否有效，关键在于能否还原成明文。

我们来分析一下这两个矩阵方程，看这两个密钥矩阵A，B之间的关系。由于AX=C，X=BC，则有ABC=C，即AB=E，所以在保密通信中，密钥只有一个，解密密钥是通过这个关系式AB=E得到的，也就是加密密钥和解密密钥互为逆矩阵B=A-1。

比如，在2008年谍战大片《潜伏》中，地下工作者余则成收到王翠平传递来的秘密消息，是20个数字，这个消息可以用一个4行5列的矩阵来表示

保密通信问题是当今信息时代发展的一个重要研究课题，实际的加密模型相当复杂，上面所举的例子只是为了说明逆矩阵应用的一个最简单的模型。

线性代数的应用例子还有很多。比如在数字图像处理中，简单的应用有：图像的变暗或变量可用矩阵的数乘来实现；图像旋转可用矩阵的转置、矩阵的线性变换来实现；图形复原可用矩阵的逆来实现；图像的分割可用矩阵子块的提取来实现等等。

线性代数的应用非常广泛，它是最有趣的一门数学课程，也是最有用的一个应用工具，因此在实际教学中必须响应其它学科的需求，从具体的、实际的例子出发来介绍概念、原理、理论的发展，这样才能让学生在后续课程的学习中体会到线性代数这门课程的重要作用。