朴素贝叶斯算法的综述

山东省济宁育才中学 王华宇

在当今这个信息技术高速发展的时代，人们对信息处理的方式越来越多样化、智能化，像人工检索这种耗时耗力的方法已经逐渐跟不上时代发展的潮流了，而迅速快捷、对人力要求甚微的人工智能正在一步步发展起来，这对于我们在大量数据中寻找、筛选对自己有用的信息是有极大的帮助的。而作为人工智能的一个分支，朴素贝叶斯算法在统计学中具有与决策树、神经网络相媲美的应用前景，因此，如果做好朴素贝叶斯算法的应用，将其应用于信息筛选，必将产生极大的作用。

一、朴素贝叶斯算法的原理

朴素贝叶斯算法是基于贝叶斯定理与特征条件独立假设的分类方法。即假设给定对象的各个属性之间相互独立，因此在计算概率时可利用公式：

之后通过计算给定对象的先验概率，利用贝叶斯定理：

计算其后验概率，即该对象属于某一类的概率，再比较各后验概率的大小，最后确定给定对象属于的类别。

朴素贝叶斯算法的具体描述（这里应用了极大似然估计）：

假设给定一数据集X ＝｛x1，x2，x3…xn｝，每个x 含有m 个属性，记为c1，c2，c3，…，cm。每个x 一一对应一个Y ＝｛y1，y2，y3，…，yn｝通过给出数据可以计算先验概率P（Y）；此时给出一个已知各属性，未知其映射yi的量Xi（c1i，c2i，c3i，…，cmi），分别计算y1，y2，y3，…，yn后验概率P（Y|Xi），比较各后验概率大小，取最大值P（Y|Xi）max，则其对应的yi即为Xi所对应的Y。

二、朴素贝叶斯算法的缺点分析

由于未知对象属性具有的不确定性，因此可能出现未知对象某一属性在原始对象中没有对应属性的情况，在该种情况下，在计算先验概率时会出现概率等于零的情况，这样就会对最终结果产生一定的影响，使结论与实际情况产生偏差。为了避免这种误差的出现，我们在极大似然估计方法的基础上可以采用贝叶斯估计，即：

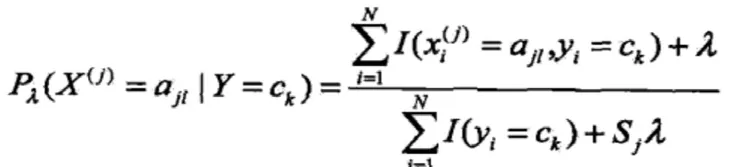
J ＝1，2，3…，n；l ＝1，2，…，Sj；k ＝1，2，…，K。

式中，xi（j）是第i 个样本的第J 个属性；ajl是第j 个属性可能取的第l 个值；I 为指示函数。

同样，先验概率的贝叶斯估计是：

式中，λ ≥0，相当于在对未知对象相应属性求取频数时赋予一个正数λ ＞0，这就是贝叶斯估计。当λ=0 时，就是极大似然估计。对于λ，我们常取1，这时称为拉普拉斯平滑。这样我们就避免了上文所提到的可能出现的误差。

三、关于朴素贝叶斯算法应用的思考

通过以上对朴素贝叶斯算法原理及具体过程的分析可以了解到：朴素贝叶斯算法对于已知部分数据并可求出数据各属性对应映射Y 的先验概率的情况下，求一未知对象Xi相应的对应映射Yi的问题具有得天独厚的优势：1.由于前提条件中进行了条件独立性假设，因此可以将计算变得简单；2.虽然进行了较强的条件独立性假设，但对于结果准确性的影响不大。

因此，如果可以将朴素贝叶斯算法与人工智能相结合，便可以在数据筛选中起到重要作用，比如日常生活中我们经常遇到的垃圾邮件，就可以利用朴素贝叶斯算法，具体方法如下：

首先随机选取等量的正常邮件和垃圾邮件，选取合适的多个属性，并利用统计学方法分别对两类邮件的各个属性的数据进行统计、分析，计算出“正常邮件”和“垃圾邮件”的先验概率，然后对于给定一已知各属性数据、未知类型的邮件，根据其各属性数据分别求出“正常邮件”和“垃圾邮件”的后验概率，比较其大小，取最大值，将其对应的邮件类型标记给上述给定邮件，若为垃圾邮件，则被系统自动删除；若为正常邮件，则由系统保留。当然，以上的计算过程、取最大值过程以及判断标记处理过程都是利用人工智能来完成的，这就实现了对朴素贝叶斯算法的应用，于是就可以准确、简便、高效地筛选出垃圾邮件并将其删除，从而提高了信息利用的效率。

本文主要讲述了朴素贝叶斯算法的基本原理、具体描述、应用的思考以及实例的分析操作。通过本文我们了解到朴素贝叶斯算法的应用在数据筛选和分类过程中的应用前景，但是朴素贝叶斯算法同时存在着一些问题，例如先验概率可能为零的情况，这里我们可以利用贝叶斯估计来代替极大似然估计，从而解决这一问题。我相信，在对朴素贝叶斯算法的不断发展和完善的过程中，一定可以发挥其更大的应用潜力，为大数据时代的人类做出更大的贡献。