钢-铅粘接结构的粘接强度对超声体波反射与透射特性的影响∗

孙凯华 李建文 孙朝明 葛继强 王增勇 高 伟

(中国工程物理研究院机械制造工艺研究所 绵阳 621999)

0 引言

粘接结构与焊接、铆接等连接方式相比，具有应力分布均匀、稳定性高、成型工艺性好以及制造成本低等优点，已被广泛应用于航空航天、武器、机械制造等领域。但这种结构在生产、使用以及长期贮存过程中，易受不良粘接工艺或不当贮存和适用条件影响，会在粘接层处出现气孔、局部脱粘、老化或强度退化等问题，严重影响粘接结构的完整性和性能质量。因此，对粘接结构的粘接层质量进行无损检测与评估具有重要意义。

粘接质量问题主要分两类：脱粘缺陷和粘接强度退化。其中，粘接强度又包括内聚强度和界面粘附强度[1]。超声检测作为粘接质量最常用的无损检测方法之一，具有对人体无害、穿透性强、指向性好、灵敏度高等特点。对于粘接结构中出现的气孔、脱粘等缺陷，常规超声检测方法(如脉冲反射法和透射法等)已经能够很好地检测出来。对于界面粘附强度减退和内聚强度弱化的检测和评估，目前采用的超声检测方法主要有超声非线性方法[2−6]、导波法[1,7−10]以及体波斜入射法[1,11−14]等。

Rothenfusser等[2]利用有限元理论计算了铝-环氧树脂-铝三层粘接结构中超声波非线性系数与粘接层厚度及粘接强度的变化关系。Hirsekorn[3]理论研究了粘接结构层中粘接力对超声透射波和反射波的非线性影响，利用超声信号的非线性参量来表征粘接强度的大小，并利用实验进行验证。李明轩等[4]、安志武等[5]建立了粘接结构的非线性弹簧模型，对楔形粘接结构进行了非线性超声检测，结果表明高次谐波对粘接强度较为敏感。江念等[6]提出了基于水浸脉冲透射法的非线性超声检测方法，利用信号时频分析和小波变换等方法来提取非线性超声特征参量，进而用于表征钢和有机玻璃的粘接强度。然而由于目前非线性检测的理论研究还不够深入系统，以及非线性检测实验中各种非检测目标的非线性及噪声等对结果的影响较大等问题，粘接强度的超声非线性检测与评价工作有待进一步开展研究。

导波法依据粘接结构中传播的导波的速度、频散及模态变化等特性来表征粘接强度。Singher[7]通过理论计算结合实验验证的方式研究了超声导波的速度变化与粘接强度之间的关系。Castaings[8]利用SH波对粘接结构的界面强度进行表征，实验检测和有限元仿真结果表明，SH0模态导波的波形幅值对粘接强度的变化较为敏感。Gauthier等[9]利用超声Lamb波的频散曲线和衰减系数对铝-环氧树脂粘接结构的界面强度变化进行了有效表征。艾春安等[1]、常新龙等[10]利用Lamb波的频散特性曲线对固体火箭发动机壳体中的脱粘缺陷以及粘接强度的变化进行了有效检测。虽然导波的速度、频散等特性对于粘接强度的变化较为敏感，但在实验检测中噪声以及导波多模式的时域混叠对于脱粘缺陷的检测和粘接强度的评估是不利的，需要合适的时频分析方法对导波的模式进行识别，同时导波检测对于粘接结构的厚度也有一定的要求。

斜入射法通过斜入射到结构中的超声波的反射特性来判断粘接质量。Rokhlin等[11]利用超声斜入射方法对粘接结构的胶层固化过程进行了检测。Rose等[12]基于弹簧边界模型利用超声斜入射法对铝-有机玻璃-铝粘接结构中界面刚度变化进行了系统的理论研究，通过实验验证表明超声斜入射的反射系数对界面粘接强度的变化比较敏感。吴斌等[13]等在浸水斜入射条件下对超声的透射系数进行了数值计算，分析了粘接界面刚度变化对弱粘接结构透射系数的影响，并通过试验验证了理论数值计算的正确性。艾春安等[14]利用超声斜入射波的反射系数对粘接强度的变化进行了仿真计算和实验检测，结果表明，在特定频率和入射角组合情况下，采用超声纵波斜入射法可实现对粘接结构界面强度的定量检测。

由上述分析可知，目前对于粘接强度的检测研究主要是利用超声体波或导波结合界面简化模型针对界面粘附强度进行分析研究，对粘接内聚强度变化的研究相对较少。而在界面粘附强度检测研究方面，大部分学者采用的是改变一种检测参数而固定其余参数的方法(如固定入射波模式、频率、胶层厚度等参数来改变入射角)来研究反射系数或透射系数随该参数的变化规律，再通过有限改变固定参数进一步分析反射透射系数的变化情况，从而找出对界面强度变化敏感的超声检测参量。由于固定参数选取的离散性以及检测参数变化的单一性，利用上述方法得到的粘接结构中的超声传播规律可能不够全面和透彻，对于超声检测参量的选取及其对粘接强度敏感程度的研究和分析还不够系统和深入。针对以上问题，本文以钢-环氧树脂-铅粘接结构为例，采用超声斜入射法来系统研究粘接强度对超声波传播特性的影响规律。本文采用传递矩阵法推导了斜入射超声波在N层粘接结构中反射与透射系数方程，依据弹簧模型和等效弹性模量模型来表征粘接强度，通过同时连续改变两种参数来系统研究粘接层界面粘附强度与内聚强度变化对超声波反射与透射特性的影响关系，确定能够敏感表征粘接强度的超声参量，为粘接强度的无损检测与评价提供理论依据。

1 多层结构中超声传播理论及粘接强度模型

对于N层粘接结构，设每层材料均为各向同性，不考虑y方向时超声斜入射粘接结构为x-z平面内二维平面应变模型，如图1所示。在超声的传播过程中，每层介质中都存在向正负方向传播的纵波和横波(DL、DT、RL、RT)，声波沿x轴和z轴进行分解得到的分量分别用u和w表示，如DL=u+L+w+L。在第n层介质中，所有声波位移矢量沿x轴的总分量un与z轴的总分量wn可表示为

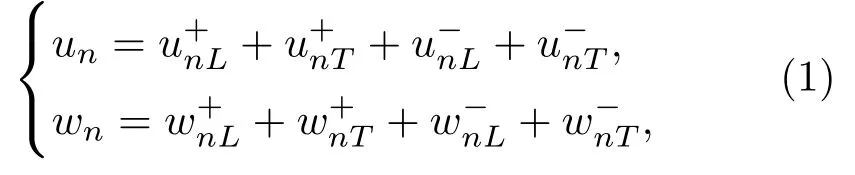
式(1)及下文公式中的所有下标n均表示第n层材料，n=1∼N，下标L和T表示分别纵波和横波，上标‘+’和‘−’对应波的传播方向为正向和负向。分量un与wn中不同方向的纵波和横波分别表示为

其中，AnL、AnT、knL和knT分别为第n层材料中纵波、横波的位移振幅和波数，θnL和θnT分别为纵波、横波的传播方向与法向的夹角(如图1所示)，ω为角频率。依据Snell定律，有

图1 超声斜入射多层粘接结构的反射与透射模型Fig.1 The ref l ection and transmission model of the ultrasonic bulk waves oblique incident in the multi-layer adhesive structure

因此，式(2)和式(3)中的最后一项均相等，并且各层中的ξn也相等，有ξn= ξn−1。

在各项同性材料中，设(σxz)n= τn,(σzz)n=σn，依据应力应变与位移的关系并利用拉梅常数与声速关系λn+2µn= ρnµn= ρn可以得到关于位移应力分量Bn={un,wn,τn,σn}T与位移幅值矢量An={,A,,}T的关系式：

式(5)中，上标m=1、2表示该层材料的下界面和上界面，矩阵[)]n表示如下：

利用式(7)可将位移应力场从下界面转换到上界面，此即为经典的Thomson传递矩阵方法[15]。

对于非理想粘接情况，引入界面刚度来表示粘接界面的粘附强度变化[12]。在第n层材料的上界面处，位移与应力的连续条件满足式(8)：

其中，KTn−1和KNn−1分别为第n层与第n−1层介质间界面处的切向与法向刚度分量，联立式(7)、式(8)可得

其中，[Kij]为界面刚度转换矩阵，[Cij]−1为该层介质上下边界的传递矩阵，则[Fij]=[Kij][Cij]−1即为相邻两层介质上界面位移应力场的传递矩阵。通过式(9)进行递归可得

则

其中，AN={DL,DT,0,0}。当入射波为纵波时，={1,0,RL,RT}；而当入射波为横波时，={0,1,RL,RT}。进一步通过式(11)最终可推导得到N层粘接结构中超声波斜入射的反射系数与透射系数方程：

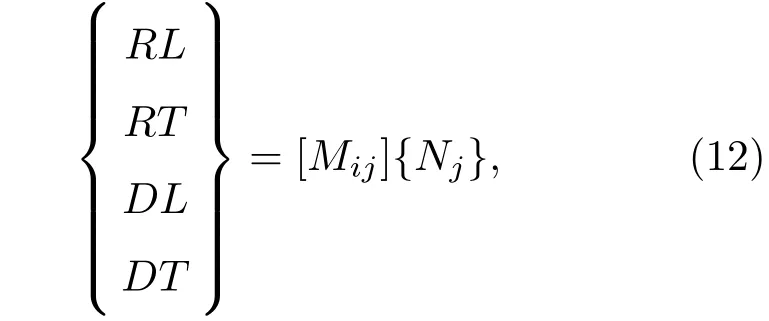
方程中的矩阵[Mij]和{Nj}可由式(12)计算得到。

界面粘附强度按照严重程度可分为三种情况，理想粘接、弱粘接和脱粘。理想粘接时，界面处的位移和应力均连续；弱粘接时，法向位移连续而切向位移不连续；完全脱粘时，法向和切向位移均不连续。对于粘接界面的粘附强度弱化，采用式(8)所示的线性弹簧模型来简化表征，通过界面刚度参数来表示界面两侧位移的不连续程度，从而反映界面粘附强度的弱化情况。其中，利用切向刚度来表征剪切粘附强度，利用法向刚度来表征拉伸粘附强度，通过连续变化的界面刚度参数来反映粘附强度的变化情况。

粘接结构在使用或长期的贮存过程中，受环境条件、载荷等因素影响，胶层会逐渐老化。在老化过程中，环氧树脂胶层主要受热氧老化和湿氧老化行为影响[16−17]，会出现降解、失重、吸水、塑化等现象，引起弹性模量、密度等的变化从而导致内聚强度的退化。因此，内聚强度τ可以表示为

其中，E、ρ、υ分别为胶层的弹性模量、密度和泊松比，ε为胶层的固化参数。在粘接工艺条件确定后，ε为不变量，Lavrentyev等[18]的研究结果表明，内聚强度的弱化主要体现在胶层弹性模量的降低上，而胶层密度在热氧老化和湿热老化的共同作用下改变较小，与弹性模量的变化相比可以忽略。因此，本文采用弹性模量变化的百分比η来简化表征胶层内聚强度相同比例的弱化情况，

2 理论计算结果及分析

利用超声波的反射与透射特性对粘接质量进行检测，需要从利于检测的角度来选取超声参数。首先，要有稳定的参考系，即在理想粘接条件下，声波的反射或透射系数要稳定，随声波参数(如声波入射角、频率等)的改变要小；其次，要对被检测对象的变化敏感，即超声参数的选定要保证反射或透射系数对粘接质量的变化灵敏；最后，检测适用范围要广，即超声参数的选定要保证反射或透射系数既能反映粘接界面强度的减弱又能检测粘接内聚强度的退化。因此，超声参数的选定需要结合多方面的因素综合考虑。

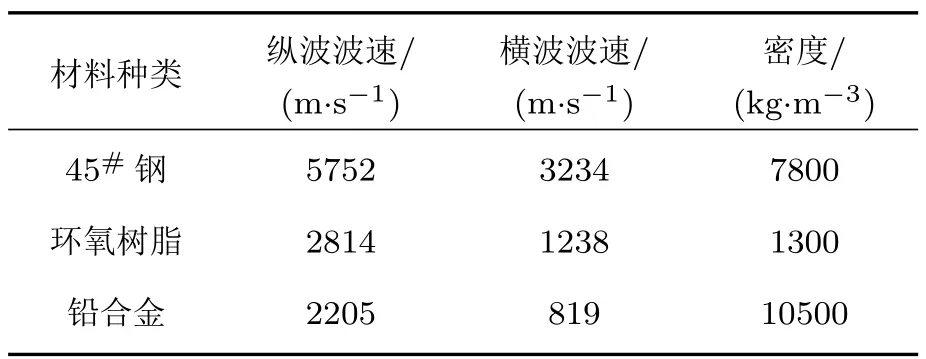
表1 材料参数Table 1 Material parameters

基于上述方法，本文以3层钢-环氧树脂-铅粘接结构为对象进行理论计算，系统研究不同入射面、不同声波模式、入射角度、频率以及不同胶层厚度、界面刚度和弹性模量情况下斜入射超声波的反射系数与透射系数，从而确定能够敏感表征粘接界面粘附强度和内聚强度的超声参数。三种材料的相关参数如表1所示。其中，钢层和铅层为粘接结构的基体材料，厚度设为半无限大，环氧树脂为粘接剂，厚度为d。

2.1 超声入射频率和胶层厚度对反射和透射特性的影响

当超声体波斜入射在粘接结构上时，超声波的反射与透射特性会受入射面、入射角度、频率、模式、胶层参数等多种因素共同影响，若固定其他条件单一改变一个参数来研究超声波的传播特性，结果可能不够全面和直观。因此，本文通过同时改变两种参数来揭示粘接结构中超声波的传播规律。图2(a)计算了纵波垂直入射钢层时的反射系数随超声频率和胶层厚度变化的关系，而图2(b)则给出了横波在10◦斜入射钢层时透射系数随频率和胶层厚度的变化关系。图中，颜色值表示纵波反射系数(RL)或横波透射系数(DT)的幅值大小。分析可知，随着声波频率和胶层厚度变化，RL或DT出现了明显的谐振现象，并且当其他参数固定不变时，RL(或DT)与入射频率f、胶层厚度d满足如下关系：

即RL(或DT)是关于频厚积(fd)的函数，频厚积不变，反射系数或透射系数不变。改变其他参数，在多组不同条件下计算RL(或DT)随f和d的变化，均可以得到式(15)所示关系。这一结果表明，f和d对反射透射系数的影响是相互关联的，因此，下文将把频厚积(fd)作为一个变量来对粘接结构中超声的反射透射特性进行分析研究。另外，由于粘接结构反射透射特性的影响因素较多，限于篇幅原因，本文只对计算结果中与入射波模式相同的反射波与透射波特性进行研究，不分析与界面作用后形成的模式转换波的反射与透射特性。

图2 超声体波反射透射系数与频率、粘接层厚度的关系Fig.2 The relationship between the frequency,the adhesive layer thickness and the ref l ection and transmission coefficients of ultrasonic bulk waves

2.2 不同入射面、声波模式条件下超声频厚积、入射角度对反射和透射特性的影响

对于钢-环氧树脂-铅粘接结构，其上下层基体材料为异种材料，选择不同的超声入射面对反射透射特性的影响存在差异。理想粘接情况下，当超声波从钢层斜入射时，声波模式分别为纵波和横波，反射、透射系数随频厚积、入射角度的变化关系分别如图3(a)、图3(b)和图4(a)、图4(b)所示。图中，颜色值表示反射或透射系数的幅值大小，RL、DL分别为纵波的反射、透射系数，RT、DT分别为横波的反射、透射系数。由图3可知，当纵波在0◦∼30◦范围内斜入射时，随着频厚积的增加，反射和透射系数均出现较为一致的谐振，谐振周期约为1.4 MHz·mm，在谐振频厚积处，RL的谐振谷极小值约为0.3，DL的谐振峰极大值约1.3，此时，DL>0.7条件下的透射窗口宽度约为0.5 MHz·mm。随着纵波入射角度的增加，谐振频厚积向高频方向微弱偏移，当入射角大于30◦后，谐振数逐渐增加，谐振现象逐步呈现无规律化，RL迅速减小，DL>0.7的透射窗口逐渐变窄，并且窄窗口数目增加。

由图4所示，当横波在0◦∼15◦范围内斜入射时，随着频厚积的增加，反射和透射系数也出现了一致的谐振，谐振周期约为0.62 MHz·mm，在谐振频厚积处，RT的谐振谷极值约为0.2，DT的谐振峰极值约为1.5，此时，DT>0.7条件下的透射窗口宽度约为0.3MHz·mm。当横波在15◦∼34◦范围内斜入射时，谐振频厚积存在无规律的微弱偏移，谐振数不变，RT迅速减小，谐振谷变宽变多，而DT仅有微弱下降，DT>0.7的透射窗口宽度几乎不变。而当横波入射角大于34◦时，由于第三临界角的存在，反射系数和透射系数的分布出现明显变化，主要表现在RT显著增加，DT明显降低且透射窗口变少变窄。

图3 超声纵波斜入射钢层时反射、透射系数与入射角、频厚积的关系Fig.3 The relationship between the frequency-thickness,incident angle and the ref l ection and transmission coefficients of longitudinal waves oblique incident in the steel-layer

图4 超声横波斜入射钢层时反射、透射系数与入射角、频厚积的关系Fig.4 The relationship between the frequency-thickness,incident angle and the ref l ection and transmission coefficients of shear waves oblique incident in the steel-layer

同样在理想粘接情况下，当超声纵波和横波分别从铅层斜入射时，反射、透射系数随频厚积、入射角度的变化关系分别如图5(a)、图5(b)和图6(a)、图6(b)所示。由于纵波在铅层中的速度小于钢层中的横波波速，超声波从铅层入射时会存在第一和第二临界角。与从钢层入射相比，反射和透射系数的分布受临界角影响变得更加复杂，当超声波入射角小于第一临界角(22◦)时，出现谐振的位置和谐振周期基本不变，DL和DT明显降低，透射窗口变窄，RL和DL的极值点会随入射角增加向高频方向偏移；当超声波入射角大于第二临界角(42◦)时，DL和DT会出现明显的增强，这是由于铅层中已经不存在透射纵波和横波，能量集中在界面处，此时在透射系数分布图中是界面波的形式体现而非严格意义的透射体波。如图6所示，当横波入射角大于第三临界角后，RT始终为1，以界面波形式存在的透射波也逐渐变弱。

对比上述结果可知，声波从铅层入射时，理想粘接条件下的反射和透射系数受临界角影响随入射角的变化较大，可用的入射角范围较小，并且低反射和高透射窗的宽度均较声波从钢层入射时窄，透射系数也较小，因此，利用超声波从铅层斜入射不利于粘接质量的检测。当超声波从钢层小角度(小于30◦)入射时，相比于反射系数，透射系数随入射角的变化较小，谐振峰比较稳定，同时透射波能够携带更多的粘接层信息，并且又由于反射与透射系数具有一定的关联性和一致性，因此，采用透射系数能够更好地表征粘接质量。综上所述，下文将主要分析超声从钢层以小于30◦入射的条件下，粘接界面强度和内聚强度变化对透射系数的影响，不再对反射系数进行分析研究。

图5 超声纵波斜入射铅层时反射、透射系数与入射角、频厚积的关系Fig.5 The relationship between the frequency-thickness,incident angle and the ref l ection and transmission coefficients of longitudinal waves oblique incident in the lead-layer

图6 超声横波斜入射铅层时反射、透射系数与入射角、频厚积的关系Fig.6 The relationship between the frequency-thickness,incident angle and the ref l ection and transmission coefficients of shear waves oblique incident in the lead-layer

2.3 界面粘附强度变化对透射特性的影响

依据线性弹簧模型，利用界面刚度系数来表征界面粘附强度的变化。设钢层与环氧树脂胶层界面为理想粘接，其法向界面刚度KN2为2×1018N/m3，切向界面刚度KT2为1×1018N/m3，而设环氧树脂与铅层界面为强度弱化界面，且法向粘附强度与切向粘附强度同时弱化。通过同时改变弱化界面的法向刚度KN1和切向刚度KT1，研究界面强度弱化对透射系数的影响。当纵波和横波分别垂直入射钢-环氧树脂-铅粘接结构时，透射系数随界面刚度和频厚积的变化关系如图7所示。如图可知，当界面刚度大于1015N/m3时，该界面可视为理想粘接，无论纵波还是横波入射，均存在明显的谐振透射峰，随着界面刚度的减小，谐振透射峰逐渐向高频方向发生频移，频移范围约为0.5 MHz·mm，并且纵波入射情况下的透射峰随刚度的减小频移量较大，同时，低频谐振峰的频移量要大于高频峰。当界面刚度继续减小到1012N/m3以下时，此时认为界面完全脱粘，透射系数趋近于0。当环氧树脂胶层的上下两个界面同时弱化时，透射系数与界面刚度和频厚积的关系如图8所示。与图7结果对比可知，当胶层两个界面的强度同时退化时，透射系数的频移范围更大(大于1.0 MHz·mm)，同样的，频厚积越小，频移越明显。

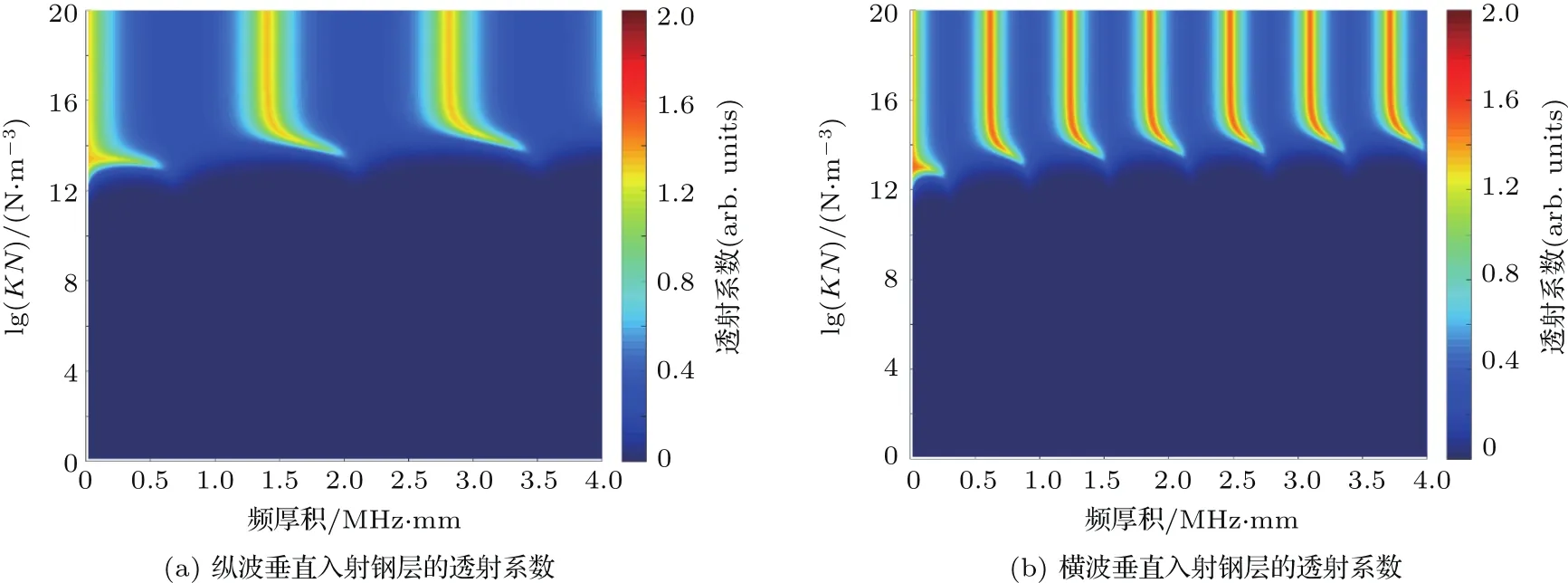
图7 胶层下界面弱化时超声体波垂直入射钢层的透射系数与频厚积、刚度系数的关系Fig.7 The relationship between the frequency-thickness,interface rigidity and the transmission coefficients of bulk waves vertical incident in the steel-layer with one interface disbanding

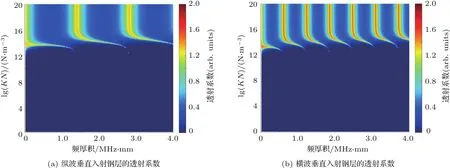
图8 胶层双界面同时弱化时超声体波垂直入射钢层时透射系数与频厚积、刚度系数的关系Fig.8 The relationship between the frequency-thickness,interface rigidity and the transmission coefficients of bulk waves vertical incident in the steel-layer with two interface disbanding

选取理想粘接条件下透射峰的频厚积，当纵波入射时设fd=1.4 MHz·mm，当横波入射时设fd=0.65 MHz·mm，连续改变胶层双界面处的法向与切向刚度，研究透射系数随入射角和界面刚度变化的关系，如图9所示。结果表明，在小角度入射条件下，透射系数对界面刚度的变化非常灵敏，在0◦入射时透射系数随界面刚度变化的改变量最大；而随着入射角度的增加，透射系数随界面刚度的变化减小。上述结果表明，从理想粘接退化到界面脱粘的过程中，小角度入射的声波透射系数的频移对界面强度的变化比较敏感。

粘接界面强度退化还存在另一种情况——弱粘接，即界面的拉伸粘附强度不变，剪切强度退化，对应于界面刚度则可表示为法向刚度不变，切向刚度迅速减小。针对这一情况，设定法向界面刚度KN1=KN2，均为2×1018N/m3不变，同时改变胶层上下两个界面处的切向刚度，研究透射系数与切向界面刚度和频厚积的变化关系，如图10所示。结果表明，当纵波垂直入射时，随着切向刚度的减小，透射系数无任何变化；而横波入射时其透射系数出现了与图8(b)相一致的结果，谐振透射峰逐渐向高频方向发生频移。进一步，将频厚积固定在理想粘接条件下的谐振峰位置处，当纵波入射时设fd=1.4 MHz·mm，当横波入射时设fd=0.65 MHz·mm，改变超声波的入射角，研究切向刚度变化对透射系数的影响，如图11所示。图11(a)的结果表明，当纵波在0◦∼30◦范围斜入射时，DL几乎不随切向刚度的变化而变化，仅在KT=1×1014N/m3的小范围内存在一个极小值，并且随着入射角度增加进一步减小；在30◦∼45◦范围内，DL随KT的减小有略微增加；而当角度进一步增大时，DL几乎不随切向刚度发生变化。这一结果说明，纵波入射时其透射系数对切向刚度的变化不敏感，不适用于界面弱粘接的检测。而当横波斜入射时，在0◦∼40◦的范围内，DT对切向刚度的弱化均非常敏感。

图9 胶层双界面同时弱化时超声体波斜入射钢层的透射系数与入射角、刚度系数的关系Fig.9 The relationship between the interface rigidity,incident angle and the transmission coefficients of bulk waves oblique incident in the steel-layer with two interface disbanding

图10 胶层剪切强度退化时超声体波垂直入射钢层的透射系数与频厚积、切向刚度的关系Fig.10 The relationship between the frequency-thickness,tangential interface rigidity and the transmission coefficients of bulk waves vertical incident in the steel-layer with shear strength disbanding

图11 胶层剪切强度退化时超声体波斜入射钢层的透射系数与入射角、切向刚度的关系Fig.11 The relationship between the tangential interface rigidity,incident angle and the transmission coefficients of bulk waves oblique incident in the steel-layer with shear strength disbanding

分析比较上述结果可知，对于从理想粘接退化到界面弱粘接(滑移界面)的过程中，小角度入射的横波的透射系数对界面强度比较敏感，可以利用低频横波的频移来表征弱粘接强度的变化。

2.4 内聚强度变化对透射特性的影响

采用式(14)所示的等效弹性模量模型来同比例地表征粘接内聚强度的变化。分别利用纵波和横波垂直入射到钢-环氧树脂-铅粘接结构的钢层界面，研究透射系数随频厚积、弹性模量变化的关系，如图12所示。对比纵波和横波入射两种情况可知，随着弹性模量的减小，纵波和横波的透射谐振峰均在向低频方向频移，并且高频谐振峰随弹性模量变化的频移速度要大于低频谐振峰的；同时，在弹性模量相同时，横波的透射谐振峰的数目在相同频厚积范围内约是纵波的两倍，并且横波谐振峰曲线的斜率也要大于纵波的。这一结果表明，利用高频纵波透射系数的谐振峰频移可以敏感表征胶层弹性模量的变化(即内聚强度的弱化)。

图12 超声体波垂直入射钢层时透射系数与频厚积、弹性模量的关系Fig.12 The relationship between the frequency-thickness,elastic modulus and the transmission coefficients of bulk waves vertical incident in the steel-layer

图13 超声体波斜入射钢层时透射系数与入射角、弹性模量的关系Fig.13 The relationship between the elastic modulus,incident angle and the ref l ection and transmission coefficients of shear waves oblique incident in the steel-layer

选取理想粘接条件下透射峰的频厚积，当纵波入射时设fd=1.4 MHz·mm，当横波入射时设fd=0.65 MHz·mm，研究透射系数与入射角、弹性模量的变化关系，如图13所示。无论是纵波入射还是横波入射，透射系数随弹性模量的变化呈无规律现象，在不同弹性模量处存在多个极大值，并且随着入射角度的增加逐渐减小。该结果表明，入射角度越小，不同弹性模量处的透射系数越大。结合图12结果可得，小角度入射超声波的透射系数的高频谐振峰频移更利于粘接内聚强度的检测。

3 结论

本文采用传递矩阵法推导了斜入射超声波在N层粘接结构中反射与透射系数方程，利用线性弹簧模型来表征界面粘附强度而利用等效弹性模量模型来表征粘接内聚强度，通过同时连续改变两种参数来系统研究钢-环氧树脂-铅粘接结构中粘接强度变化对超声波反射与透射特性的影响规律，从而确定能够敏感表征粘接强度的超声参量。通过上述研究，得到以下结论：

(1)对于钢-环氧树脂-铅粘接结构，超声体波从钢层斜入射比从铅层入射时更有利于粘接质量的检测。因为钢层入射的声波受临界角的影响少，只有横波入射时存在第三临界角，透射或反射系数的谐振峰(或谷)比较稳定，并且具有一定的带宽，谐振峰处的透射系数也较大，这对于粘接质量的检测非常有利。

(2)超声体波以小角度(小于30◦)入射时，利用透射系数能够更好地表征粘接质量的变化。相比于反射系数，透射系数随入射角的变化较小，谐振峰比较稳定，同时透射波能够携带更多的粘接层信息，对于粘接层的质量变化更加敏感。

(3)当粘接层粘附质量从理想粘接退化到完全脱粘时，在小角度入射条件下，纵波和横波的透射系数均对界面刚度的变化灵敏，在0◦入射时透射系数随界面刚度的变化最大，并且纵波和横波的透射系数谐振峰随着法向界面刚度的减小向高频方向偏移，谐振峰频率越低，受界面强度变化影响的频移量越大；而当粘附界面由理想粘接退化为滑移弱粘接时，仅横波的透射系数对界面刚度的变化较灵敏。因此，选择横波垂直入射，可以利用其透射系数的低频谐振峰向高频方向的偏移来表征界面粘附强度的变化。

(4)选择纵波或横波垂直入射，可以利用其透射系数的高频谐振峰向低频方向的偏移来表征界面内聚强度的变化。

本文较系统和全面地分析了多个参数条件同时变化对粘接结构中超声波反射和透射特性的影响规律，确定了能够敏感表征粘接强度的超声检测条件，对于其他各向同性材料组成的粘接结构具有普适性，能够为粘接强度的无损检测与评价提供理论依据。下一步，笔者将对该方法开展相关的有限元仿真和实验检测，验证理论方法的准确性和可靠性。