基于空耦超声的复合材料黏弹性评价方法∗

曾雪峰 常俊杰 卢 超 李光亚 罗更生

(1南昌航空大学 无损检测技术教育部重点实验室 南昌 330063)

(2日本探头株式会社 横滨 232-0033)

(3中北大学 太原 030051)

(4湖南省特种设备检验检测研究院 长沙 410000)

0 引言

复合材料因为其自身的特点目前在航空航天等领域的应用十分广泛[1−2]。随着复合材料使用环境越来越恶劣，其所处环境中的振动、噪声和冲击等不良因素往往是造成复合材料产生结构疲劳与损伤、安全寿命缩短的直接原因，而内在阻尼机制是材料安全性能的一个重要评价指标。复合材料的黏弹性是表征其内在阻尼机制的重要力学特性，为了确保复合材料在使用过程中的安全，对于复合材料黏弹性的评价就显得尤为重要了[3−7]。目前对于复合材料黏弹性的评价方法主要包括动态力学分析法(Dynamic mechanical analysis,DMA)[8−9]及超声法[10−11]等，但对于某些在役构件及特殊结构复合材料(如CFRP)等，以上方法是无能为力的，并且耦合剂和水等对复合材料的力学特性也会产生很大的影响。

空气耦合超声检测技术具有非接触、非浸润、非破坏以及无伤害的特性，非常适用于复合材料的检测[12−13]。本文主要讨论一种基于空气耦合超声的复合材料黏弹性评价方法，详细地讨论了黏弹性以及超声评价法的相关理论，并且将接触式超声底面回波法与空气耦合穿透法进行对比实验，验证了该方法的可行性和准确性。

1 检测原理

1.1 黏弹性评价方法

静态黏弹性研究和动态黏弹性研究是从不同的角度来评价材料的黏弹性。然而材料在实际工作使用当中，其所受到的作用力为动态力，所以动态力学性能比静力学性能更能反映材料在实际使用条件下的性能。动态力学实验中，正弦应力是最常用的交变应力。下面以拉伸应力为例，其表达式为

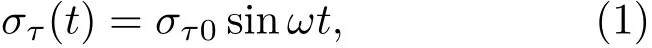
式(1)中，στ0为应力振幅；ω为角频率(rad)。

因材料性质的不同，材料在正弦交变应力作用下的应变响应也有所不同。对于理想弹性体，应变对应力的响应是瞬间的，所以应变响应是与应力同相位的正弦函数，应变表达式为

式(2)中，ε0为应变振幅。

对于理想黏性体，应变落后于应力90◦。对于黏弹性材料，应变滞后于应力一个相位角δ(0◦< δ<90◦)。当ε(t)= ε0sinωt时， 则σ(t)=σ0sin(ωt+δ)，这个应力表达式可以展开成

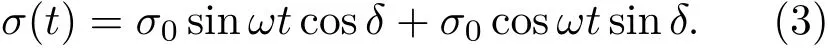
由式(3)可见，应力由两部分组成：(1)与应变同相位的应力，即σ0sinωtcosδ，这是弹性形变的主动力；(2)与应变相位差90◦的应力，即σ0cosωtsinδ，由于该应力所对应的形变是黏性形变，所以必将消耗于克服摩擦阻力上。如果定义E′为同相的应力和应变幅值的比值，E′′为相差90◦的应力和应变幅值的比值，则：

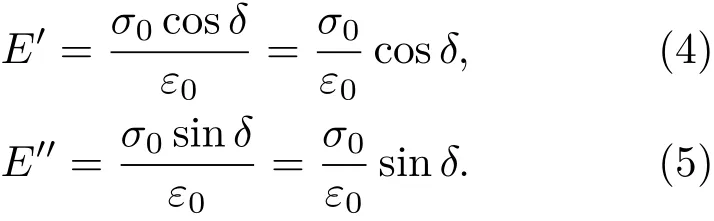
将式(4)和式(5)代入到式(3)中，应力的表达式为

因此，式(6)包括两个部分，该模量的表达式符合数学上的复数形式，称为复数模量(Complex modulus)E∗，如式(7)所示。其中E′为实数模量或称储能模量(Storage modulus)，E′′为虚数模量或称损耗模量(Loss modulus)。

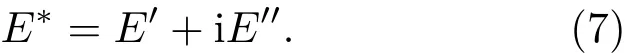
损耗角正切值计算公式如式(8)所示：

1.2 检测方法与步骤

1.2.1 接触式底面回波法

利用接触式底面回波法对材料黏弹性进行评价，检测原理如图1所示，检测步骤如下。

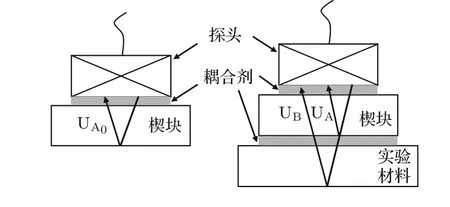
图1 接触式底面回波法原理图Fig.1 Contact bottom echo method schematic

图1中UA0为楔块底面回波信号，波形UA为楔块与实验材料界面上的回波信号，波形UB为实验材料的底面回波信号。对回波信号UA0、UA和UB进行频谱分析，得到的幅度谱分别记为A0(f)、A(f)和B(f)。由式(9)就可求得实验材料的衰减系数a(f)：

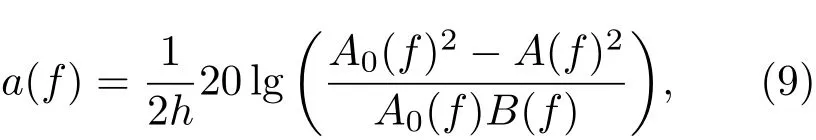
其中，h为实验材料的厚度；a(f)为实验材料的衰减系数。

通过利用各个回波的复数域频谱中的实部和虚部，可求得相速度Cp(f)：

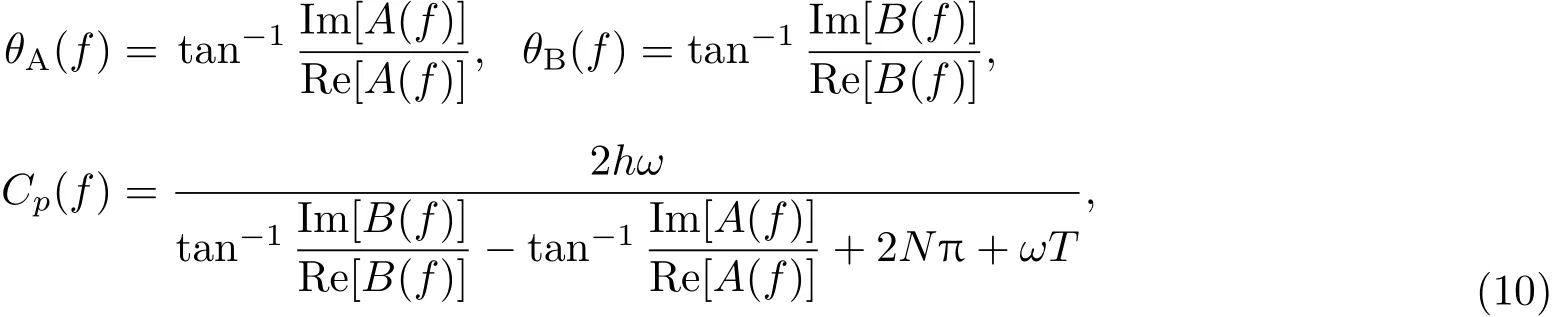
其中，f为频率，ω为角频率(ω =2πf)，T 是回波信号UA和UB在进行傅里叶变换时，取出波形的开始时间之差，T=tB−tA。

根据复数弹性理论，超声波的储能模量E′、损耗模量E′′以及损耗角的正切值tanδ可由式(11)推导。其中，假定αV p/ω≪1。

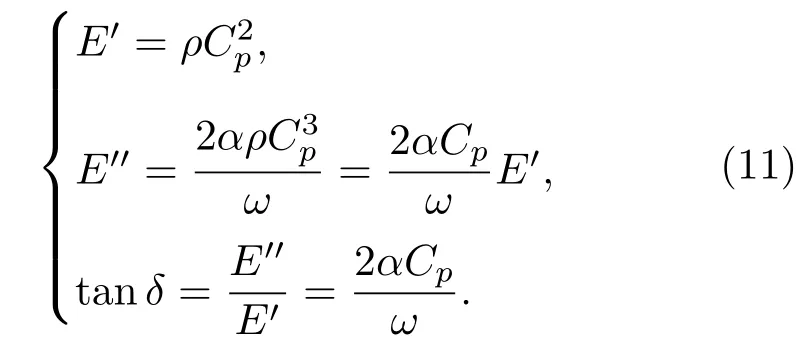
利用公式(11)，即可对材料黏弹性进行评价。

1.2.2 空气耦合穿透法

下面，利用空气耦合穿透法对材料黏弹性进行评价，评价步骤如下：

(1)分析超声波在空气中的衰减系数

当使用空气耦合穿透法对材料黏弹性性能进行评价时，计算出超声波在空气中的衰减系数a1(f)(如图2所示)。先将发射探头与接收探头之间的间距调整为h1，此时接收到的第一次波形记为UA1(如图2左)；再将发射探头与接收探头之间的间距调整为h2，此时接收到的第一次波形记为UA2(如图2右)。接下来，对接收到的波形UA1和波形UA2进行频谱分析，得到的幅度谱分别记为A1(f)和A2(f)。通过式(12)可得超声波在空气中的衰减系数a1(f)：

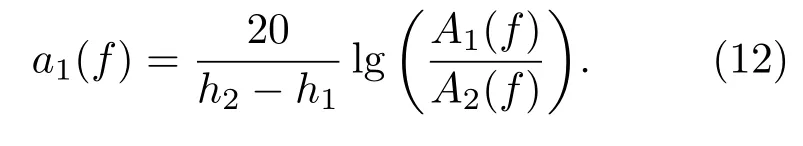
图2 计算超声波在空气中的衰减系数示意图Fig.2 Calculate the attenuation coefficient of ultrasonic waves in air

(2)实验材料与空气界面上的声压反射率r(f)

如图3所示，将发射探头与接收探头之间的距离调整到D，此时接收探头接收到的入射波记为U0(如图3左)；然后再使用单探头(超声检测方式为回波法)，将发射探头与材料上表面的距离调到D/2，此时探头接收到的界面反射波记为U1(如图3右)。最后，对信号U0和U1进行频谱分析，得到的幅度谱分别记为U0(f)和U1(f)。由式(13)可得材料与空气界面上的声压反射率：

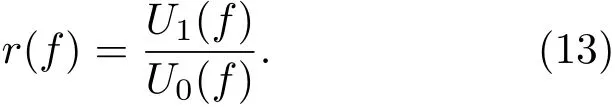
(3)超声波在材料中的衰减系数a(f)

如图4所示，首先将发射探头与接收探头之间的间距调整到H，并将此时接收到的信号记为UA(如图4左)，然后将被检材料放入发射探头与接收探头之间，保持材料与发射探头垂直，使超声波垂直入射到材料中。发射探头与接收探头间距仍然为H，此时接收到的信号记为UB(如图4右)。对接收到的信号UA和UB进行频谱分析，将幅度谱分别记为A(f)和B(f)。由式(14)可得超声波在材料中的衰减系数：

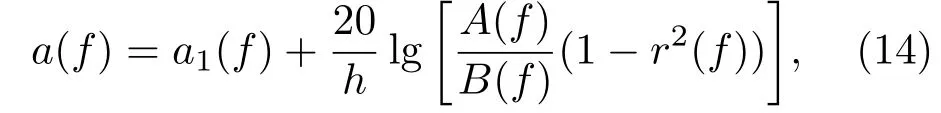
其中，h为被检材料的厚度。

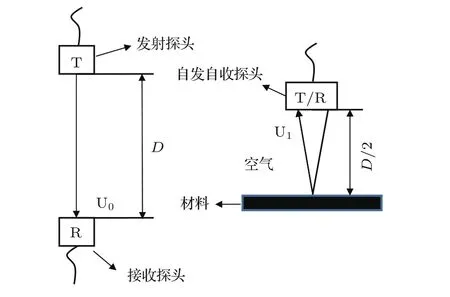
图3 计算界面声压反射率的示意图Fig.3 Calculate the interface sound pressure relf ectivity diagram

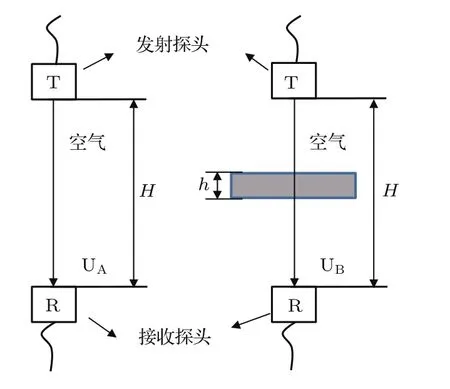
图4 两探头之间放入(不放入)实验材料的示意图Fig.4 Schematic illustration of placing(without inserting)experimental material between two probes

(4)相速度Cp(f)

根据幅度谱A(f)和B(f)，可以通过式(15)计算信号UA和UB的相位角：

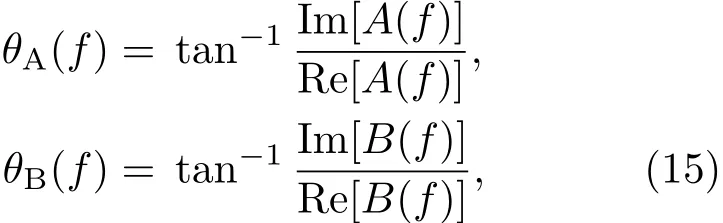
其中，Im[A(f)]为信号频谱UA的虚部；Re[A(f)]为信号频谱UA的实部；Im[B(f)]为信号UB频谱的虚部；Re[B(f)]为信号UB频谱的实部；θA(f)为信号UA的相位角；θB(f)为信号UB的相位角。根据波数的计算公式β=2πf/Cp，相速度可通过式(16)求出：

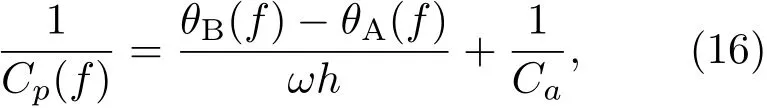
其中，ω为角速度(ω =2πf)；h为材料的厚度；Ca为空气中的声速；θB(f)、θA(f)为波形UB和波形UA的相位角。

其中，需要对公式(16)进行一个简单的说明。在公式(16)中的相位角θB(f)、θA(f)并不是波形UB和波形UA的绝对相位角，因为在对波形UA和波形UB进行频谱分析时，并不是从时间t=0开始的，而在计算信号的绝对相位角时，对信号进行频谱分析时应从时间t=0开始。所以为了得到信号的绝对相位角，在对信号进行傅里叶变换时，需要对t=0与信号开始接收时间之间的信号进行归零处理，并且对整段信号进行傅里叶变换。由于这个过程比较繁琐，为了简化绝对相位角的求解过程，可以使用下面的方式来求得超声信号的绝对相位角。

在对信号UA和UB进行频谱分析时，将信号UA和UB进行傅里叶变换时的开始时间分别记为tA和tB。则两者时间差T为

则利用信号复数域频率谱的实数部和虚数部以及时间T，可求得相速度Cp：

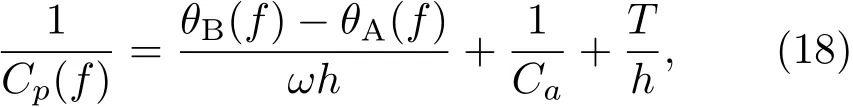
其中，f为频率，ω为角频率(ω =2πf)，Ca为空气中的波速，T为回波信号UA和UB在傅里叶变换时，取出波形的开始时间差。

根据复数弹性理论，纵波超声波的储能模量E′，耗能模量E′′及损耗角正切tanδ可由式(19)推导。这里，假定αV p/ω≪1。

利用公式(19)，即可对材料黏弹性进行评价。

1.3 接触式超声底面回波法与空气耦合超声穿透法对比

利用接触式超声底面回波法和空气耦合超声穿透法分别对同一块橡胶材料的黏弹性进行评价，并且将两种方法结果进行对比，根据对比结果来对空气耦合超声穿透法的可靠性进行验证，检测步骤如上文所述。采用橡胶材料作为实验材料，以环氧树脂作为楔块。其中，楔块尺寸为92 mm×60 mm×30 mm；实验材料尺寸为150 mm×150 mm×50 mm。接触式超声底面回波法使用的是超声纵波直探头(频率0.8 MHz、压电晶片的直径20 mm)；空气耦合超声穿透法使用的是空气耦合专用纵波平探头(频率0.8 MHz、压电晶片尺寸14 mm×20 mm)。

1.3.1 接触式超声底面回波法结果

通过耦合剂将探头与楔块进行耦合，原理如图1所示，并且将楔块底面上的回波信号记为A0，信号A0如图5(a)所示。然后，通过耦合剂将探头与楔块、实验材料进行耦合，将在楔块与材料界面上的反射回波记为波形A，将材料底面的反射回波记为波形B，此时接收到的波形如图5(b)所示。分别对波形A0、波形A和波形B的点画线区域内进行频谱分析，三者幅度谱中的峰值频率都为0.87 MHz。根据接触式超声底面回波法对损耗角正切值tanδ的计算公式，求得在峰值频率0.87 MHz处的tanδ为1.05。橡胶材料的损耗角正切值tanδ与频率的关系如图6所示。

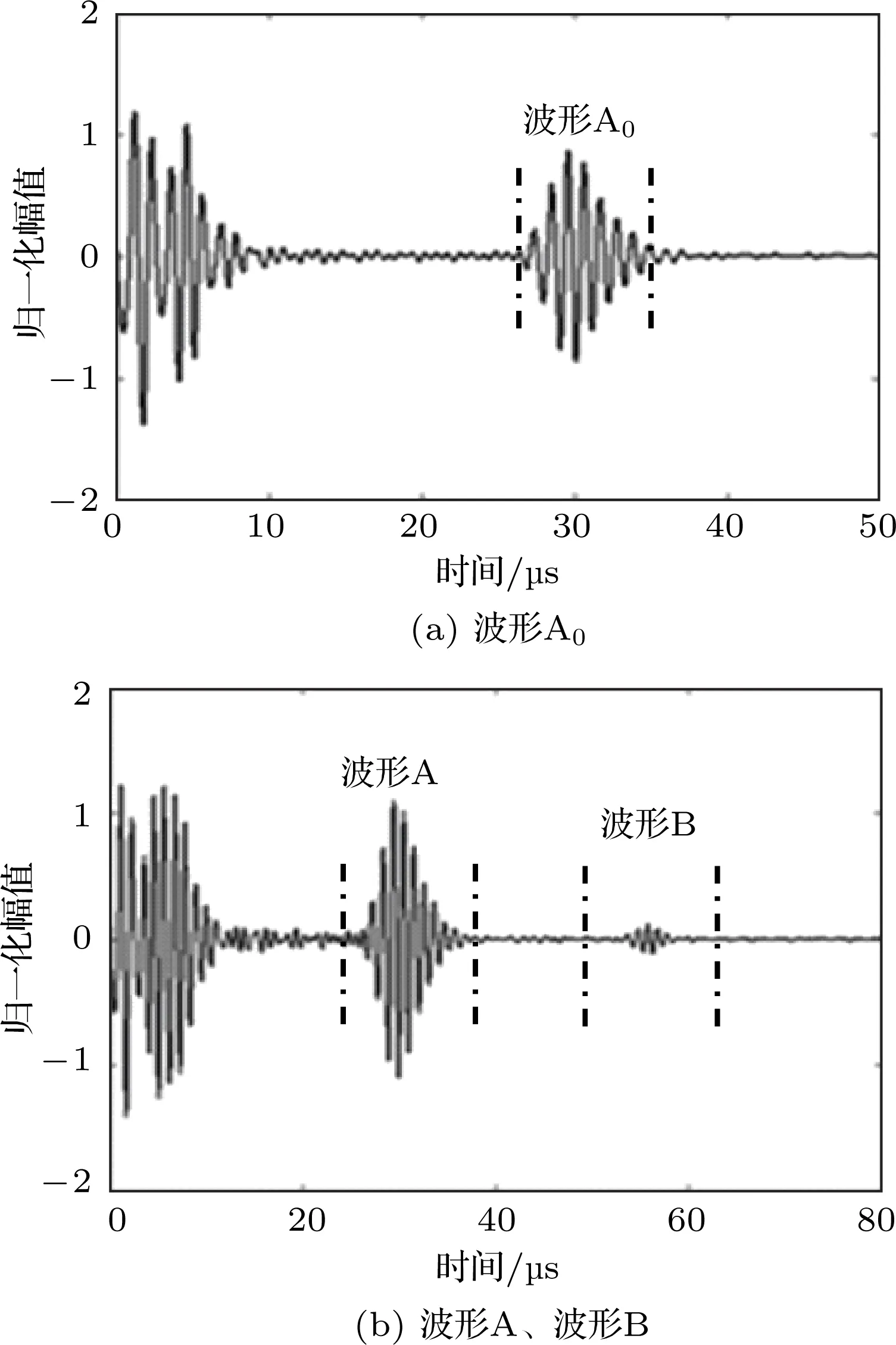
图5 波形A0和波形A、波形B示意图Fig.5 Waveform A0、A and B

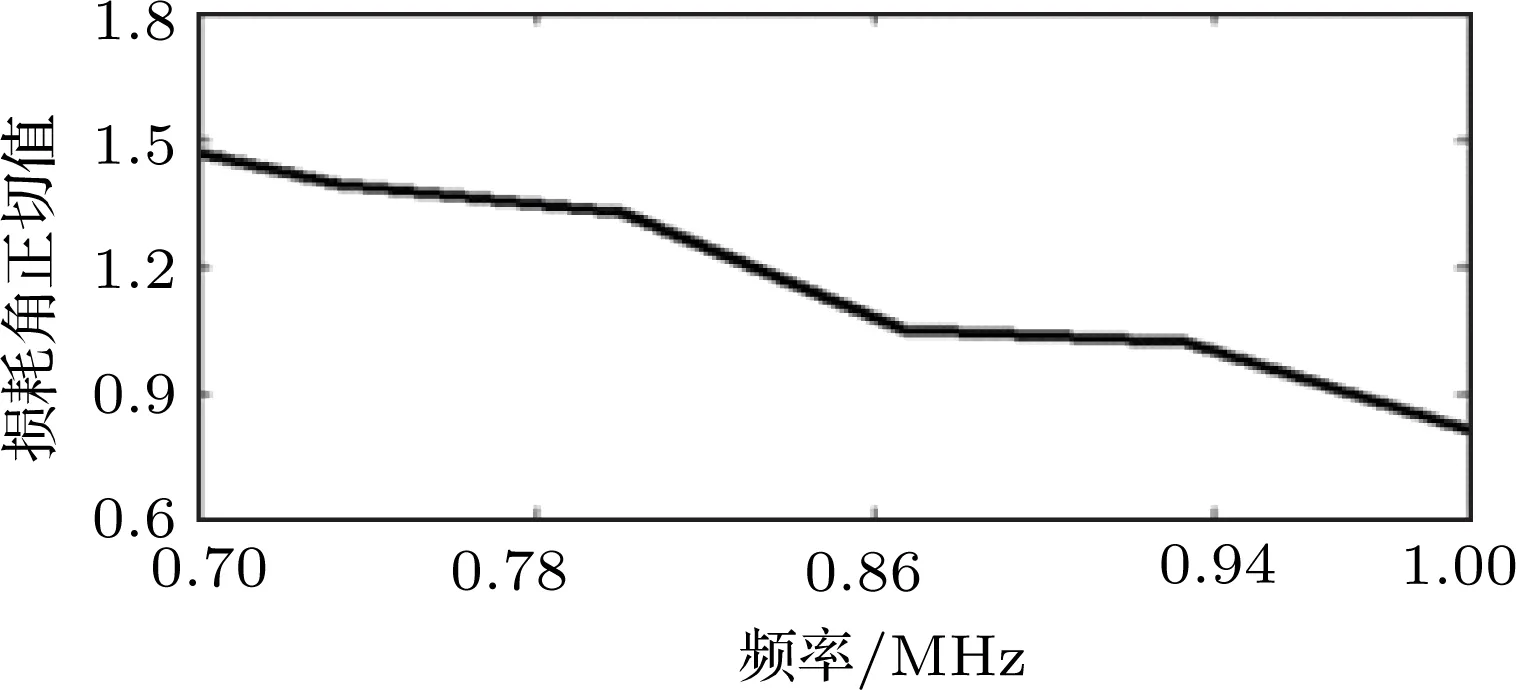
图6 橡胶材料的损耗角正切值示意图Fig.6 Loss angle tangent of rubber material

1.3.2 空气耦合超声穿透法结果

通过空气耦合超声穿透法对橡胶材料黏弹性进行评价，步骤如下：

(1)求超声波在空气中的衰减系数a1(f)

当两探头之间的间距分别为65 mm和90 mm时，探头所接收到的超声波分别记为A1和A2，其波形如图7所示。对波形A1和波形A2的第一个包络点画线区域内进行频谱分析，分别得到波形A1和波形A2的幅度谱，根据超声波在空气中的衰减系数计算公式，求出衰减系数a1(f)的结果如图8所示。

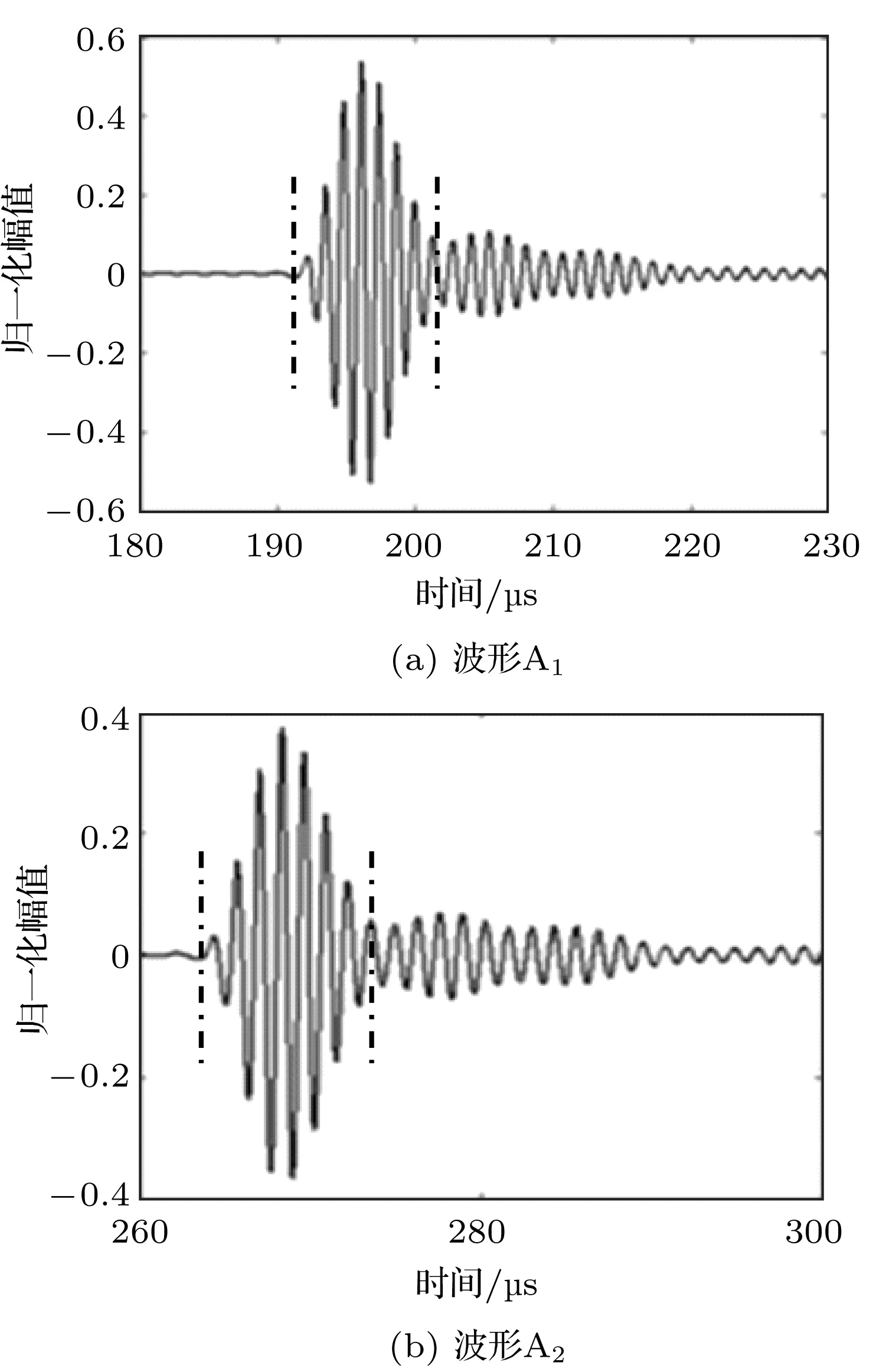
图7 波形A1和波形A2Fig.7 Waveform A1and A2

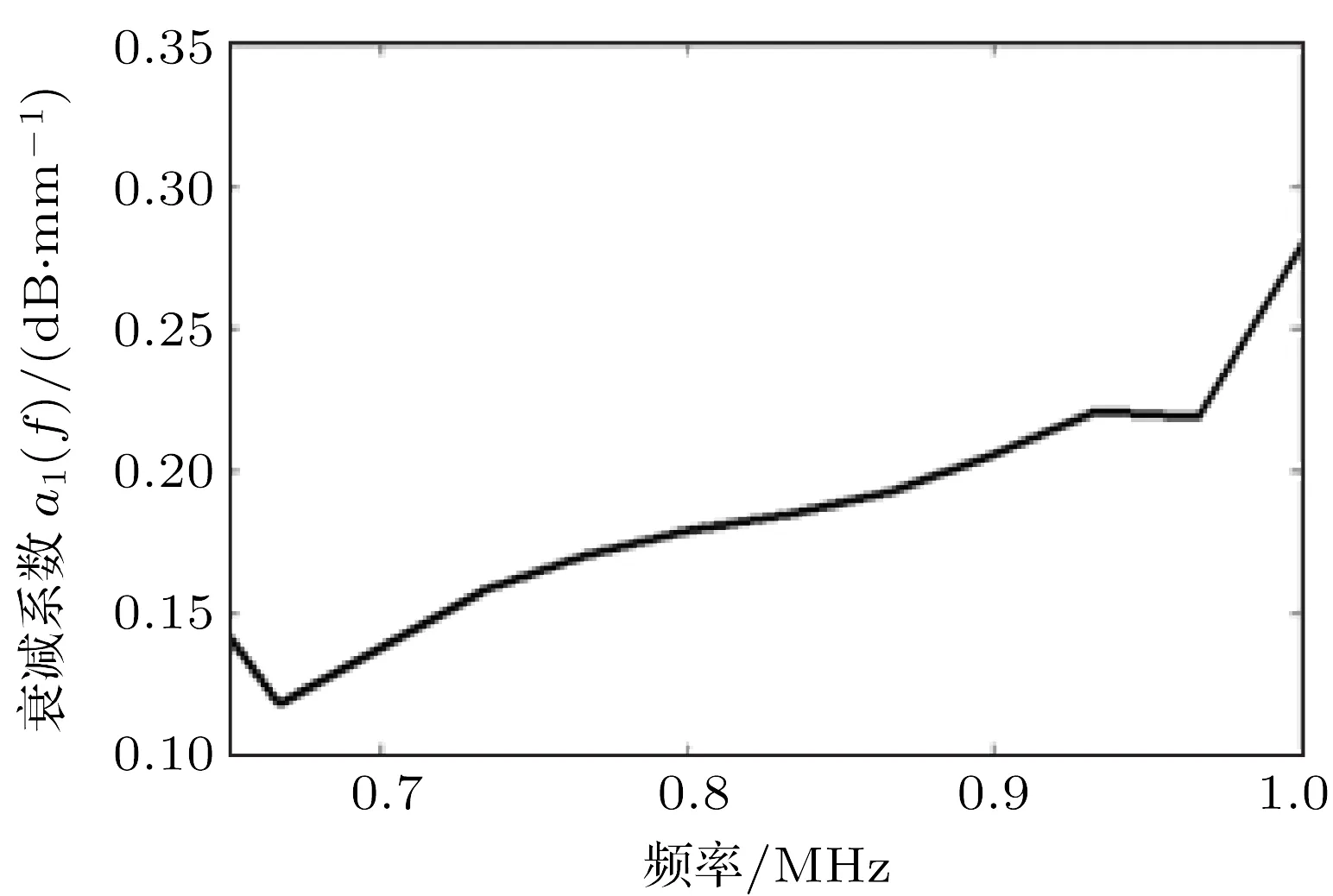
图8 超声波在空气中的衰减系数a1(f)与频率关系图Fig.8 Attenuation coefficient and frequency diagram of ultrasonic waves in air

(2)求超声波在材料中的衰减系数和相速度

保持探头之间距离不变为80 mm，在探头之间放入与不放入实验材料(橡胶)，将放入材料时的波形记为B，未放入实验材料的波形记为A，其波形如图9所示。对波形A和波形B的第一个包络点画线区域内进行频谱分析后，得到幅度谱，其峰值频率都为0.77 MHz。根据材料中超声波的衰减系数a(f)和相速度Cp(f)的计算公式，其结果如图10所示。再根据损耗角正切值tanδ的计算公式，求出实验材料(橡胶)的损耗角正切值tanδ与频率的关系如图11所示。

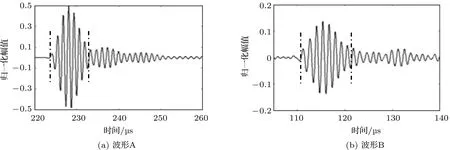
图9 波形A和波形BFig.9 Waveform A and B

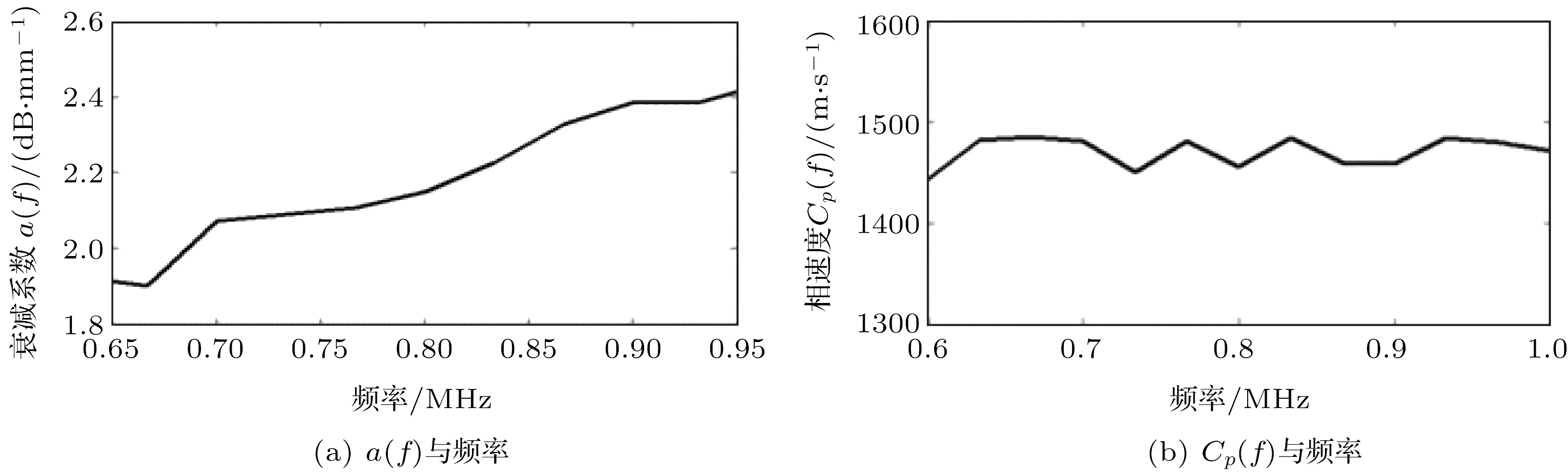
图10 超声波在材料中的衰减系数a(f)和相速度Cp(f)与频率关系图Fig.10 Attenuation coefficient and phase velocity vs.frequency diagram of ultrasonic wave in materials

图11 橡胶材料的损耗角正切值tanδ与频率关系图Fig.11 Loss angle tangent and frequency diagram of rubber material

1.3.3 结果对比及分析

使用传统接触式超声反射法和空气耦合穿透法对橡胶材料进行了评价，对结果分析可知两种方法得到的橡胶材料的损耗角正切值与频率的关系都是一致的，即损耗角正切值的数值随着频率的增加而减小，频率为0.8 MHz时，接触式超声反射法正切值为1.32；空气耦合穿透法正切值为1.24，误差小于6.1%。相对于穿透法，接触法结果有些偏差，造成这种偏差的原因是使用接触法时因楔块衰减小而未考虑超声波在楔块中的衰减。依据以上分析可以得出两种方法对于橡胶材料的黏弹性的评价结果是一致的，验证了空气耦合穿透法对材料黏弹性评价的可靠性和准确性。

2 检测系统及对碳纤维复合材料黏弹性评价

2.1 检测系统及实验对象

空气耦合超声检测系统原理图如图12所示，由计算机(基于LabVIEW的系统控制软件NUAT-21)、NI数据采集器(PXT-1033)、高功率超声信号发射接收器(Japan Probe Co.,Ltd.JPR-600C)、前置放大器(增益为60 dB)、空气耦合专用平板探头(频率为0.4 MHz，压电晶片的尺寸为14 mm×20 mm)等组成。

在材料黏弹性评价实验中，实验材料为碳纤维复合材料，其制作工艺为热压成型技术，且固化工艺都是相同的，即：真空袋压，固化温度120◦C，固化时间45 min。为了了解不同铺层方向对材料黏弹性的影响，做了一批不同铺层方向且厚度为3 mm的碳纤维复合材料，其中碳纤维复合材料的铺层方向分别为0◦、45◦/0◦和45◦/ − 45◦。碳纤维复合材料的示意图如图13所示。

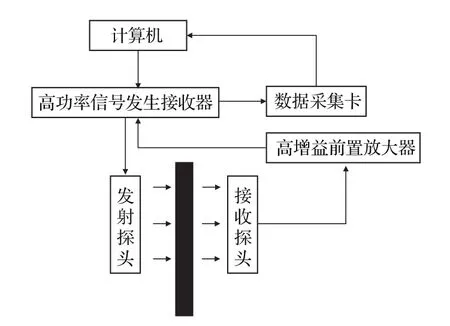
图12 空气耦合超声检测系统原理图Fig.12 Air coupled ultrasonic testing system schematic

图13 碳纤维复合材料实物图Fig.13 Carbon f i ber composite material diagram

2.2 实验及数据分析

2.2.1 铺层方向为0◦的碳纤维复合材料

(1)求超声波在空气中的衰减系数a1(f)

将两探头之间的距离分别调节为65 mm和90 mm时，将探头接收到的超声波分别记为波形A1和波形A2，其波形如图14所示。

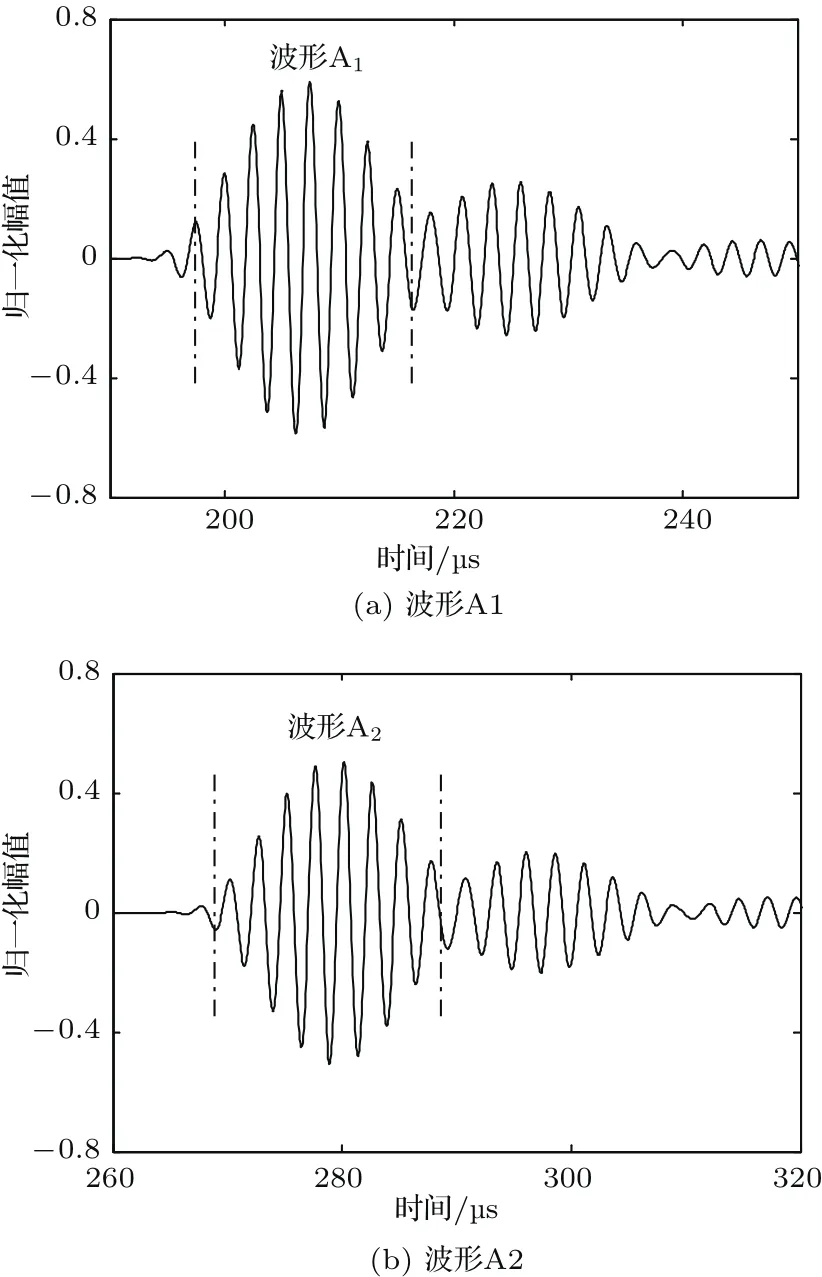
图14 波形A1和波形A2Fig.14 Waveform A1and A2

接下来，对波形A1和波形A2第一个包络点画线区域内进行频谱分析后，分别得到波形A1和波形A2的幅度谱，再根据超声波在空气中的衰减系数计算公式，可求出衰减系数a1(f)，a1(f)与频率之间的关系如图15所示。

(2)求超声波在材料中的衰减系数和相速度

将两探头之间的距离调整为90 mm时，在两探头之间，放入与不放入复合材料时，将探头所接收到的超声波分别记为波形B和波形A，如图16所示。

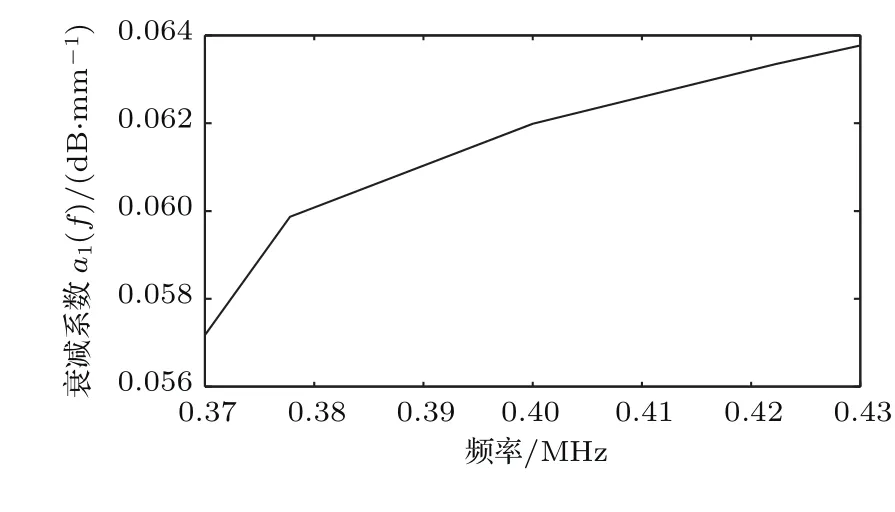
图15 超声波在空气中的衰减系数a1(f)Fig.15 Ultrasonic attenuation coefficient in air

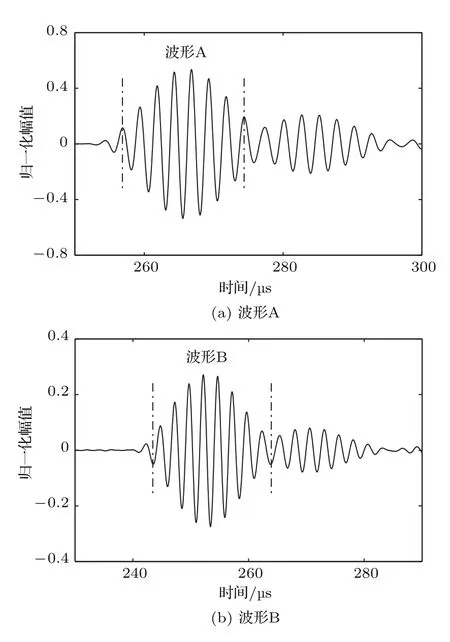
图16 波形A与波形B示意图Fig.16 Waveform A and B

对波形A和波形B的第一个包络点画线区域内进行频谱分析，分别得到波形A和波形B的幅度谱，根据超声波在材料中的衰减系数a(f)和相速度的计算公式，求出a(f)和Cp(f)，如图17所示。再根据损耗角正切值tanδ的计算公式，铺层方向为0◦的复合材料的tanδ与频率的关系如图18所示。

2.2.2 复合材料黏弹性评价结果分析

通过材料黏弹性空气耦合穿透法这一评价方法，对一批不同铺层方向的碳纤维复合材料进行了黏弹性的评价，并且得到了对不同铺层方向的碳纤维复合材料的黏弹性的评价结果。经过对上面结果

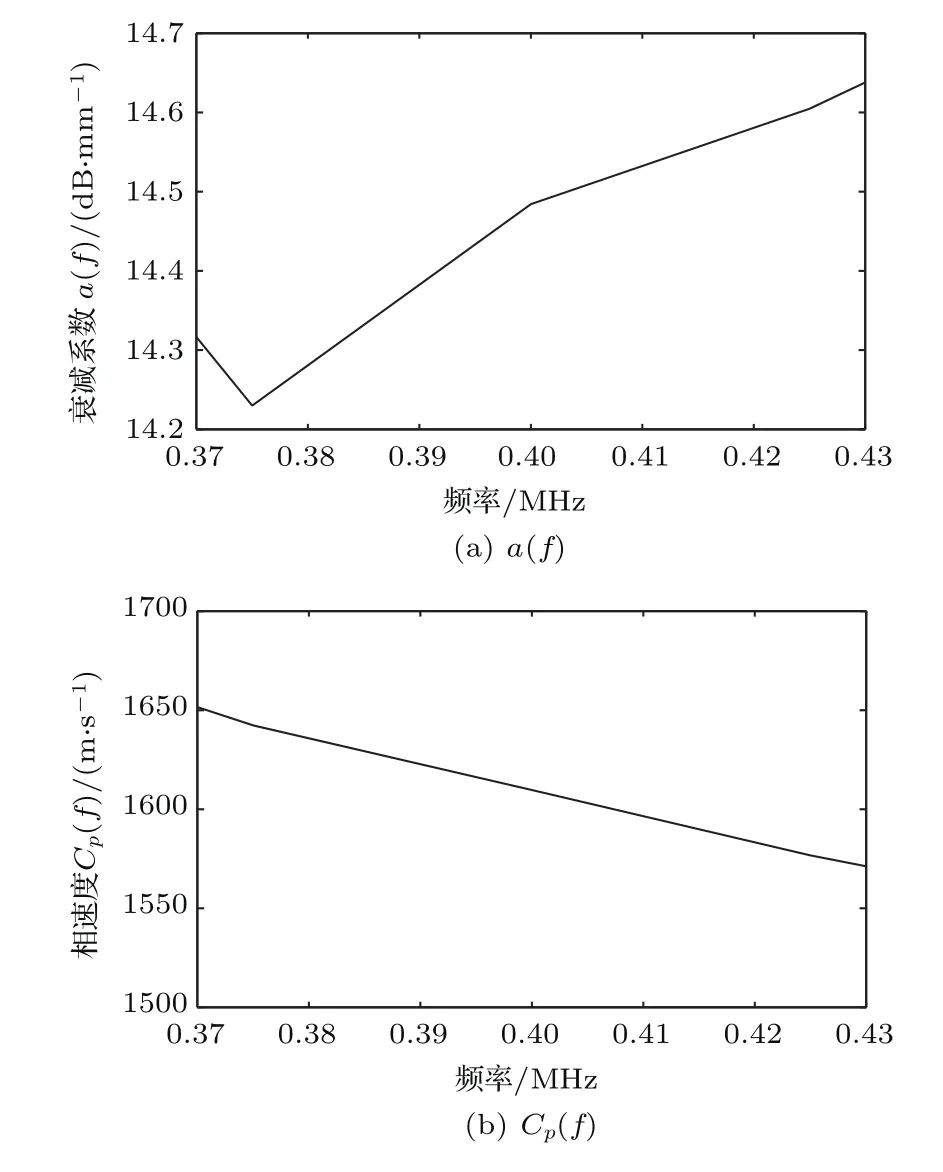
图17 超声波在材料中的衰减系数a(f)和相速度Cp(f)的示意图Fig.17 Attenuation coefficient and phase velocity of ultrasonic waves in materials

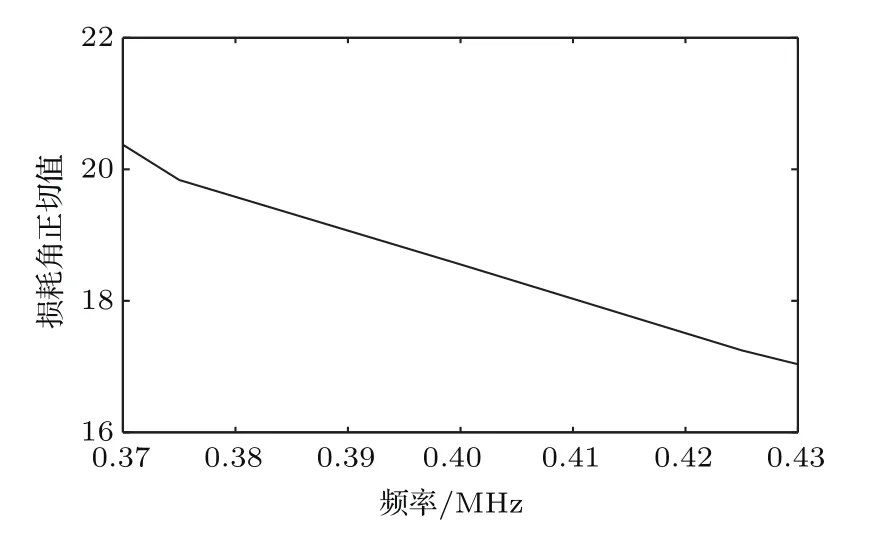
图18 0◦铺层方向的复合材料的损耗角正切值tanδ分布Fig.18 Loss angle tangent distribution of laminated composites

的整理后，得到了在不同铺层方向和不同频率下的碳纤维复合材料的损耗角正切值tanδ，如表1所示。

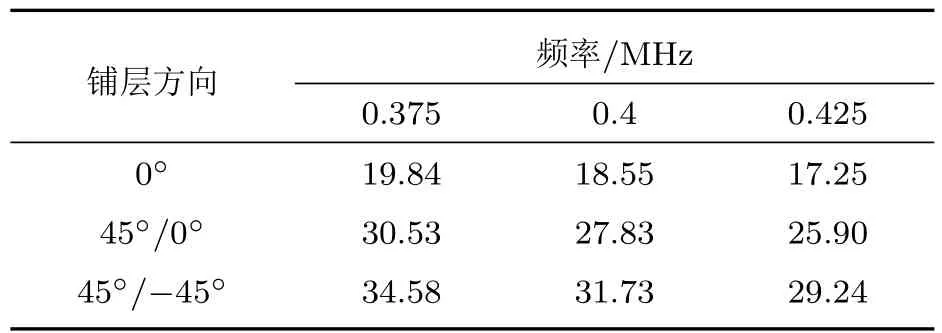
表1 碳纤维复合材料的损耗角正切值Table 1 Loss tangent of carbon f i ber composites

由以上结果可见：

(1)复合材料的损耗角正切值tanδ的数值随着超声波频率的增加而减小；

(2)铺层方向会对复合材料的黏弹性产生一定的影响，每一层预浸料的铺层方向之间的夹角越大，复合材料的损耗角的正切值tanδ越大。

3 结论

本文主要讨论了利用通过空气耦合超声穿透法对碳纤维复合材料的黏弹性进行评价的方法。将空气耦合超声波透射法与传统接触式超声波底面回波法进行对比实验，并且通过空气耦合超声穿透法分别对铺层方向为0◦、45◦/0◦和45◦/−45◦三块碳纤维复合材料的黏弹性进行评价，通过实验数据可以看出复合材料的黏弹性除了与自身铺层材料有关之外，还与超声波的频率具有近似的线性关系。实验验证了空气耦合超声法对于复合材料黏弹性评价的可行性，为复合材料的动态黏弹性及力学特征的评价提供了新的方法。