径向声子晶体隔声特性∗
2019-04-02王兴国舒海生刘秀林王凤娟
王兴国 舒海生 张 靓 刘秀林 王凤娟
(1齐齐哈尔大学机电工程学院 齐齐哈尔 161006)
(2哈尔滨工程大学机电工程学院 哈尔滨 150001)
(3黑龙江交通职业技术学院 齐齐哈尔 161002)
0 引言
声子晶体作为一种人工周期结构功能材料,具有控制波传播的特性,从而受到了学界的广泛关注[1−5]。近年来,声子晶体在带隙理论和带隙算法方面均取得重要进展。声子晶体模型是借鉴和模仿自然晶格结构形式,即在直角坐标系中构造声子晶体模型,这种周期性结构在一定程度上已经制约了该领域的进一步发展。在声子晶体带隙的产生本质上应根源于其内在的平移周期性,然而我们认为能够激发带隙的并不仅限于这种周期特性。目前,我们已经做了一些广义声子晶体方面的研究[6−8],成功地将广义周期性的理念引入到曲线坐标系和柱坐标系下,例如:在曲线坐标系下构建出广义声子晶体曲梁结构;在柱坐标系下构建出一维广义声子晶体薄圆板以及压电型广义声子晶体薄圆板。需要指出的是,Torrent等[9]提出了一类径向波晶体概念;Li等[10]和Ma等[11]构造了两类径向声子晶体,针对Lamb波在其中的传播特性进行了研究,并指出这类结构可用于结构的探伤;Ye等[12]对两种流体组成的复合球壳对中心点声源的透射系数与反射系数进行了研究,但是并没有针对固体情况进行探索,也未揭示出带隙的产生机理。
在以上研究的基础上,本文进一步构建了柱坐标系下具有径向周期性的一维径向声子晶体柱壳。柱壳的振动与声辐射问题一直是结构声学的重点,文献[13-18]分别采用解析法和数值法讨论了单双层圆柱壳的振动与声辐射性能,这些研究主要集中在圆柱壳结构受简谐力作用下的振动与声辐射,而对于内部声源作用下的周期圆柱壳的外场声辐射问题的研究较少。随着静音设备和减振隔振技术的发展,机械力引起的噪声得到了有效的控制,使得内部声激励壳体的振动及声辐射的研究更加重要。为此我们针对声波在径向声子晶体柱壳内的轴对称传播问题展开研究,力图发现一些有意义的现象并研究其产生机理,以期能够为此类结构的减振降噪提供一种新的原理和技术途径。
1 理论分析
图1为我们所构建的系统结构简图。图中,径向声子晶体柱壳是由两种不同弹性常数和密度的固体介质材料A和B在r方向上交替嵌套排列形成的一维柱状周期结构;声波入射空间和出射空间流体介质区域分别用I和II来表示。
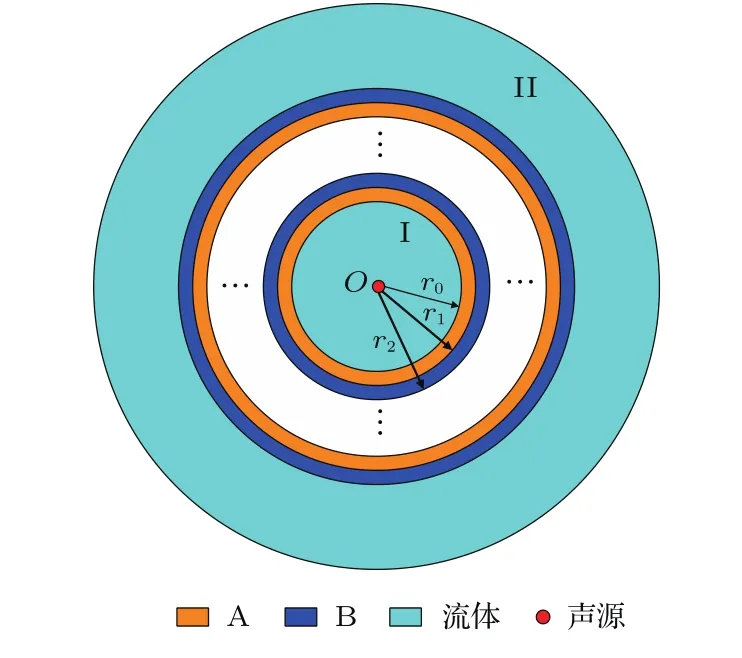
图1 线声源和径向声子晶体柱壳结构简图Fig.1 Schematic diagram of the line source and cylindrical shell of radial phononic crystals
在线声源激励下,能量的传输途径为声源-内部流体介质-径向声子晶体柱壳-外部流体介质,故柱壳内外流体介质存在声辐射,而壳体将产生振动,需对声场和结构场分别进行分析。
1.1 声场方程
线声源作用下,区域I内入射波场的声压表达式为
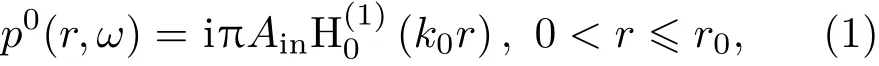
其中,Ain为待定系数,为汉克尔函数,k0=ω/c0,c0代表声腔内流体介质的声速。
由于流体介质与径向声子晶体的阻抗特性不同,在区域I内必然还存在反射波。反射波场声压的表达式为
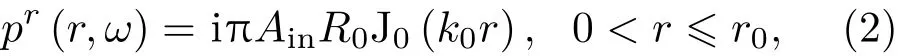
其中,R0为待定系数,J0为贝塞尔函数。
故内部声腔总的声压表达式为
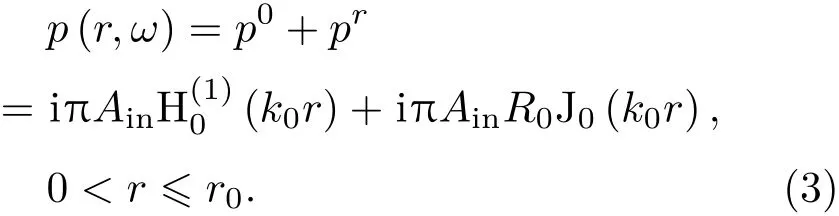
在区域II(r>r2N,N为总周期数)存在着透射声场,透射波的声压表达式为
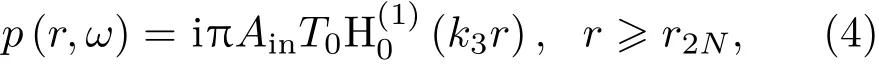
其中,T0为待定系数,k3=ω/c3,c3为外部流体介质的声速。
区域I、II声场的质点振动速度表达式为[19]
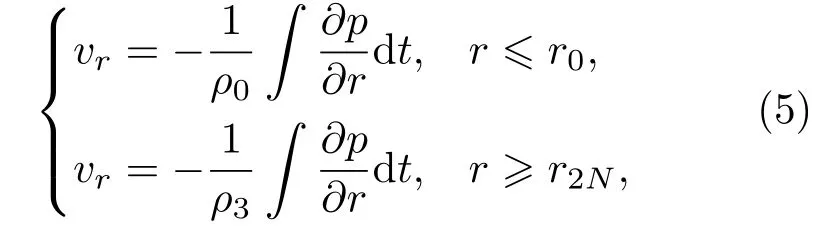
其中,ρ0、ρ3分别代表柱壳内外流体的密度。
联立式(1)、式(2)、式(4),推导出声压透射TR和反射系数RF表达式为
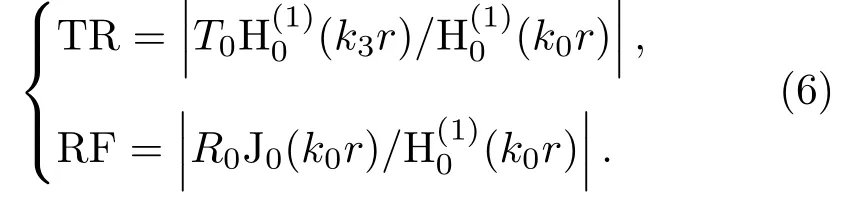
隔声量的一般通式可表示为
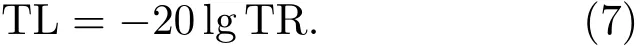
联立式(6)、式(7)即可推导出径向声子晶体柱壳隔声量的具体表达式。
径向声子晶体柱壳内外侧的声压级之差为
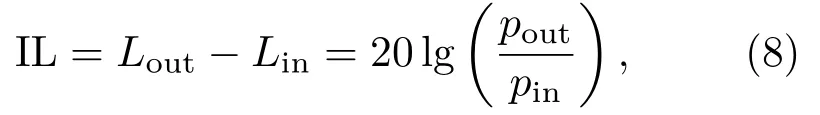
其中,IL为声压级之差,Lout、Lin分别表示柱壳内外层的声压级。式(8)中,
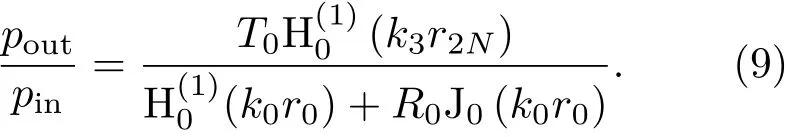
1.2 结构场方程
在中心线声源激励下,弹性固体中只存在纵波。纵波在径向声子晶体柱壳中传播的控制方程表示为[20]
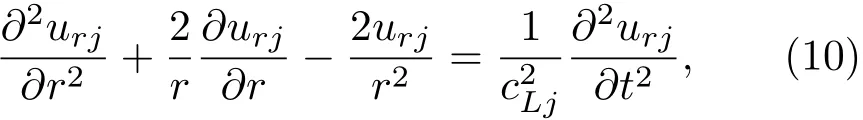
式(10)中,urj代表径向位移,cLj=为纵波的波速,λ和µ为拉梅常数,j=1,2代表任意组元中的子层1和子层2。
方程(10)的通解表示为
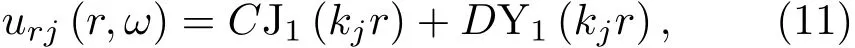
其中,C、D为待定系数,J1、Y1分别表示一阶第一类和第二类柱贝塞尔函数,kj为波数。
径向应力表示为
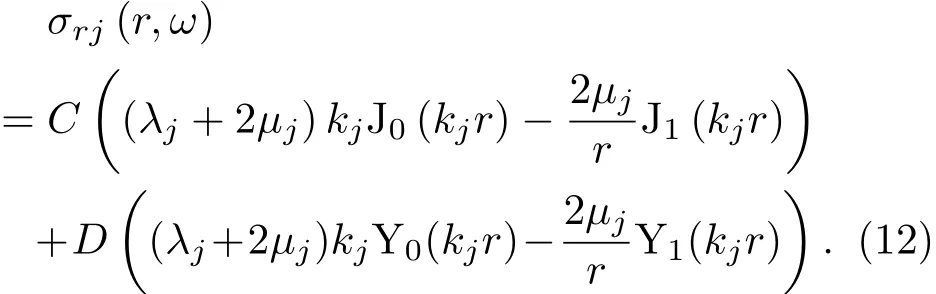
式(11)、式(12)即为径向声子晶体柱壳在声波激励下径向位移与应力的表达式。
本文重点关注的是反射声场和透射声场的大小及其分布情况,而采用力学状态向量传递矩阵法,可以直接将内外声场与结构场联立起来求解透射系数和反射系数,进而能够消除求解结构场各周期组元待定系数的复杂性。鉴于在之前的研究中详细地推导了径向波在径向声子晶体柱壳中由内向外传播的力学状态向量传递矩阵,本文在计算过程中直接引用相关方程[21]。
求解透射系数以及反射系数的前提需先求出未知系数R0和T0,应用声固耦合协调条件来进行求解,即在柱壳内壁(r0)和柱壳外壁(r2N)界面处固体和流体的法向振速相等、固体的法向正应力与流体的声压相等:
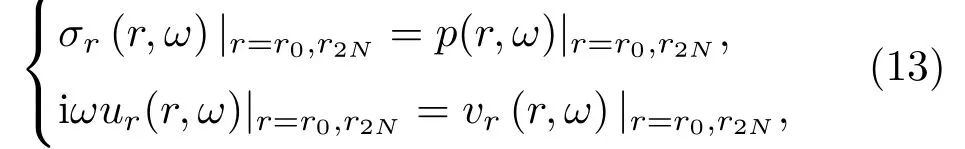
求解式(13)即可求出系数R0和T0。
2 数值计算和有限元仿真
为了能够说明问题的本质,我们进行一些数值算例分析。假定柱壳内外的流体介质为理想状态下的水(ρ0/3=1000 kg/m3,c0/3=1480 m/s);柱壳本体结构的材料参数如表1所示。
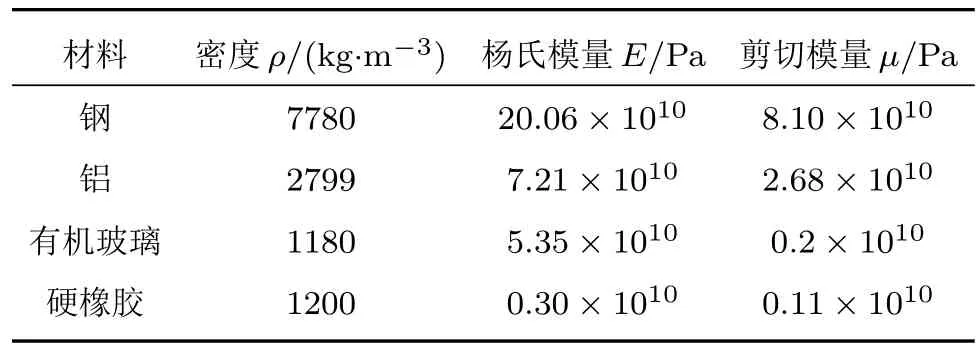
表1 线弹性材料参数Table 1 Linear elastic material parameters
2.1 单一材质柱壳隔声性能分析
2.1.1 壳体厚度(d)
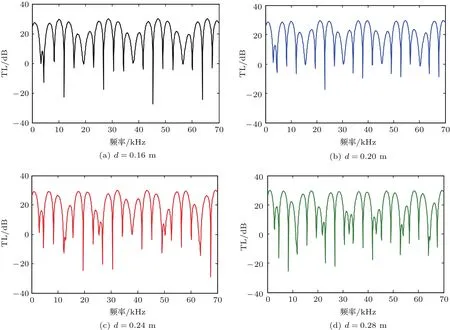
图2 声波在不同厚度钢质柱壳中传播时隔声量频响曲线Fig.2 The sound insulation frequency response curve when acoustic waves propagate in steel shells with dif f erent thicknesses
首先分析壳体的厚度对隔声性能的影响。图2给出了在声腔尺寸r0=0.2 m情况下,声波在不同厚度(d)钢质柱壳中传播时隔声量频响曲线。观察图2我们可以发现,这四条隔声量频响曲线均存在较为密集的共振峰和节点,当声波频率接近于TL曲线节点对应频率时,声波得到了一定程度上的抑制;相反,当入射声波频率接近共振峰对应频率时,该结构显然并没有起到隔声的效果。此外,由于声波多重反射的相干性,四条曲线表现出一定的周期性,其随着柱壳厚度d的增加,周期数目增多,周期变小。
纵观全图,就隔声效果而言,随着d的增加,TL曲线的数值并没有显著变化,在低频范围内(0.1 kHz∼2 kHz)TL的值有略微增加,而在高频处TL的最大值稳定在30 dB左右,显然单纯地增加柱壳厚度能够对低频声波进一步产生一定程度的抑制作用。
2.1.2 声腔尺寸(r0)
将柱壳厚度统一设定为0.16 m,分别对声腔尺寸为0.2 m、0.5 m、1.0 m和2.0 m的四种钢质柱壳进行数值计算,相应的隔声量频响曲线如图3所示。对比图3可以发现,随着声腔尺寸的扩大,隔声量频响曲线的包络线周期数目是不变的,但其峰谷数目增多。这表明声腔尺寸影响峰谷的位置以及疏密程度,而壳体厚度控制着包络线的数目。
对于声腔尺寸的增大意味着波阵面的扩大,文献[7]已经证明了波阵面对近场波的作用较为明显,而对远场波的影响较小,所以单材质柱壳会表现出随着声腔尺寸的增大,低频声波的衰减逐渐越小,而高频声波的衰减量几乎没有变化这一现象。
2.1.3 结构材料
由隔声质量作用定律可知,结构材料特性阻抗的不同,将导致不同材质壳体的隔声性能也不相同。图4给出了同一厚度(d=0.16 m)和声腔尺寸(r0=0.2 m)下,不同材质柱壳隔声量的频响曲线图。明显可以发现,除部分共振峰位置外,单质柱壳表现出特性阻抗越大,隔声能力越强。
2.2 径向声子晶体柱壳的隔声特性分析
针对由钢(A)、硬橡胶(B)两种材料组成的径向声子晶体柱壳进行隔声特性分析,组元及声腔的结构尺寸参数如表2所示。为了能够说明问题同时便于和单质柱壳隔声能力进行对比,此处,我们针对四周期的径向声子晶体柱壳模型进行分析。
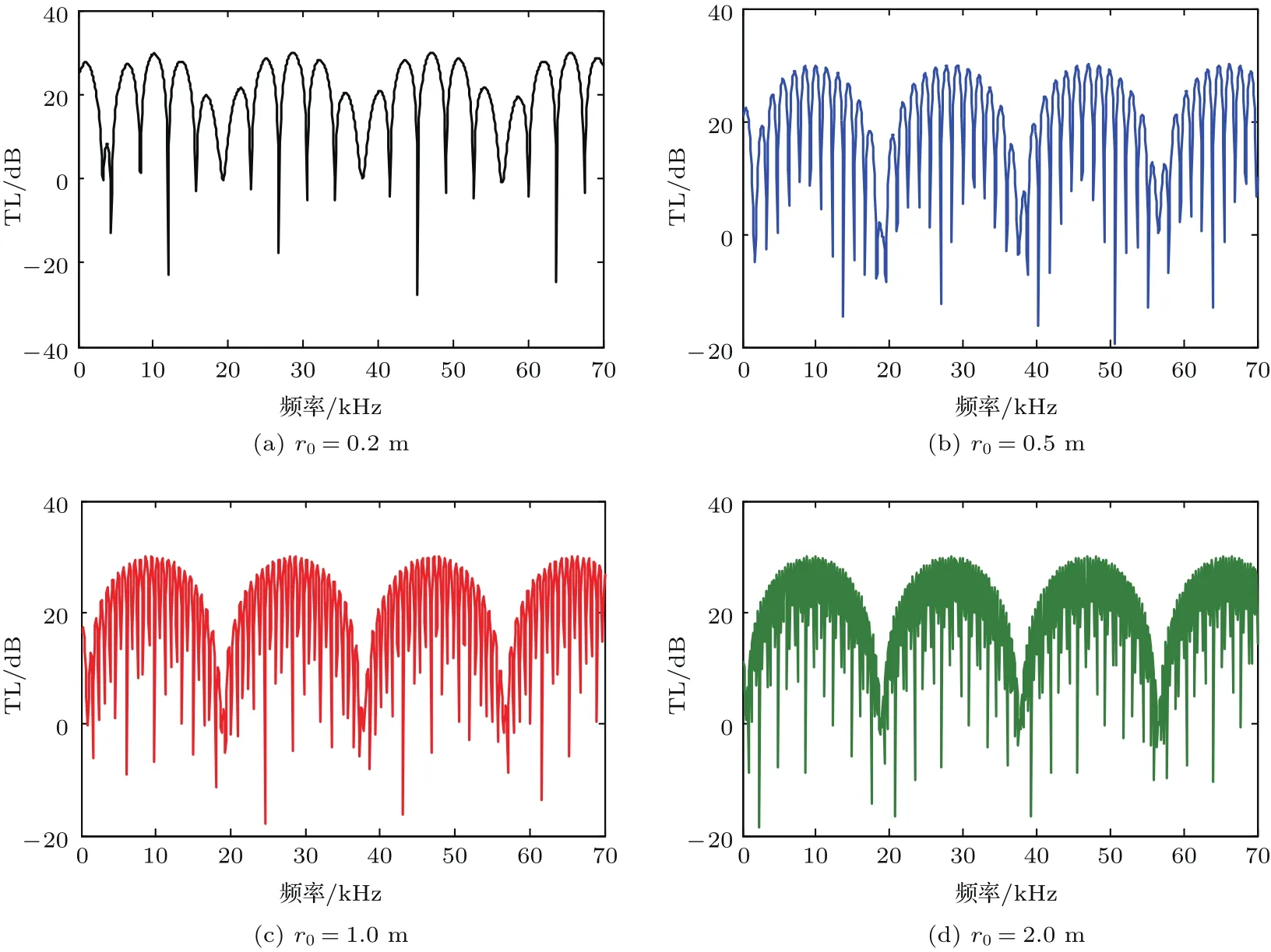
图3 不同声腔尺寸壳体的隔声量曲线Fig.3 The sound insulation curve of the shells with dif f erent acoustic cavities
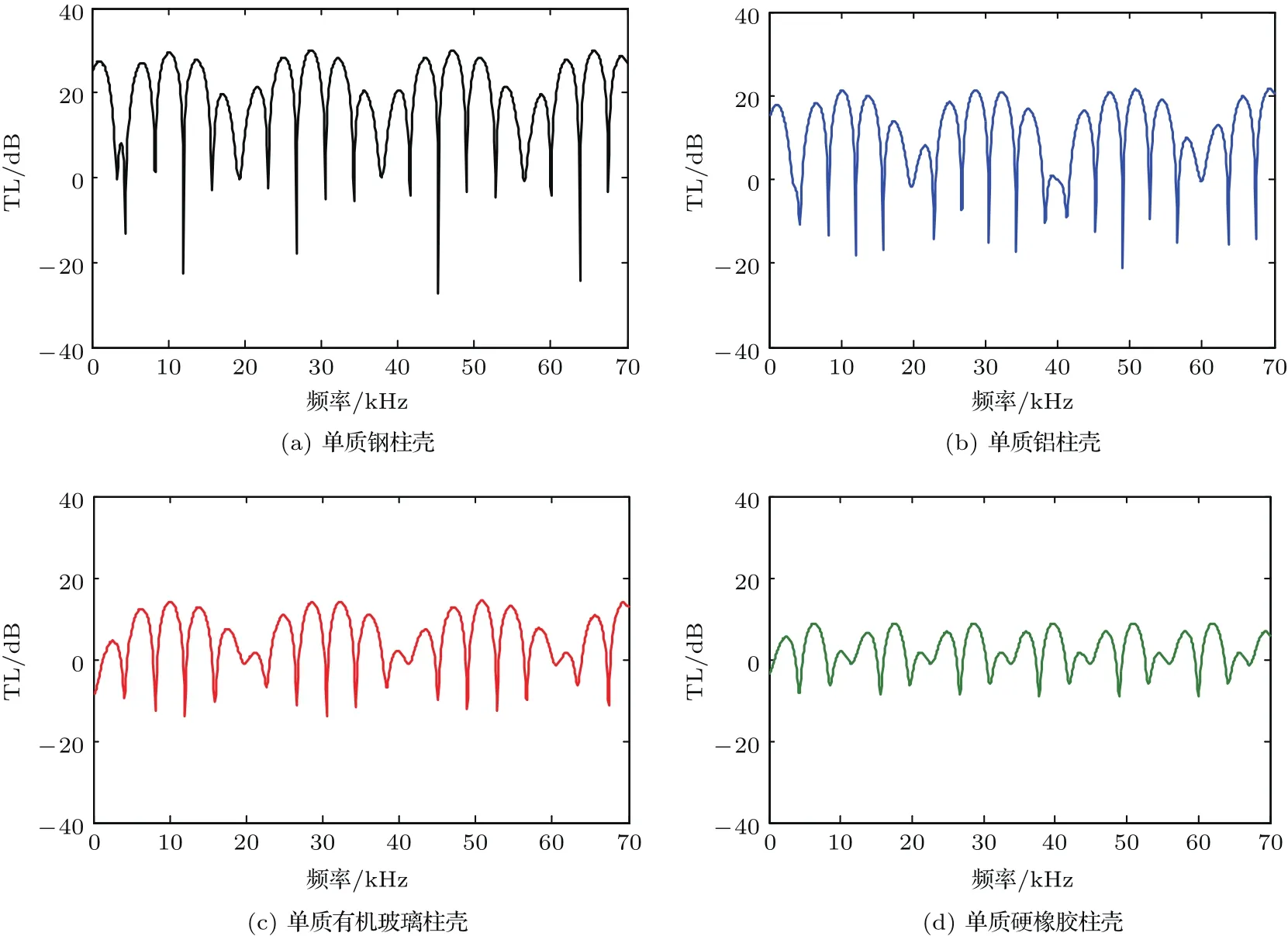
图4 不同材料壳体的隔声量曲线Fig.4 The sound insulation curve of dif f erent material shells

表2 结构尺寸参数Table 2 Structural dimension parameters
根据第1节的理论分析,对径向声子晶体柱壳的透射系数和隔声量进行计算,其计算结果如图5所示。
由图5可知,径向声子晶体柱壳在中高频域(13.2 kHz∼57.1 kHz)内均存在一个明显的声波带隙包络线。在声波带隙范围内,透射系数曲线的数值都小于1,隔声量曲线的数值都在0 dB以上,最大隔声量为86.51 dB,明显高于单质钢和硬橡胶柱壳,说明声波得到有效的抑制;而在低频范围内径向声子晶体与单一材质壳体的隔声量并没有显著的区别。
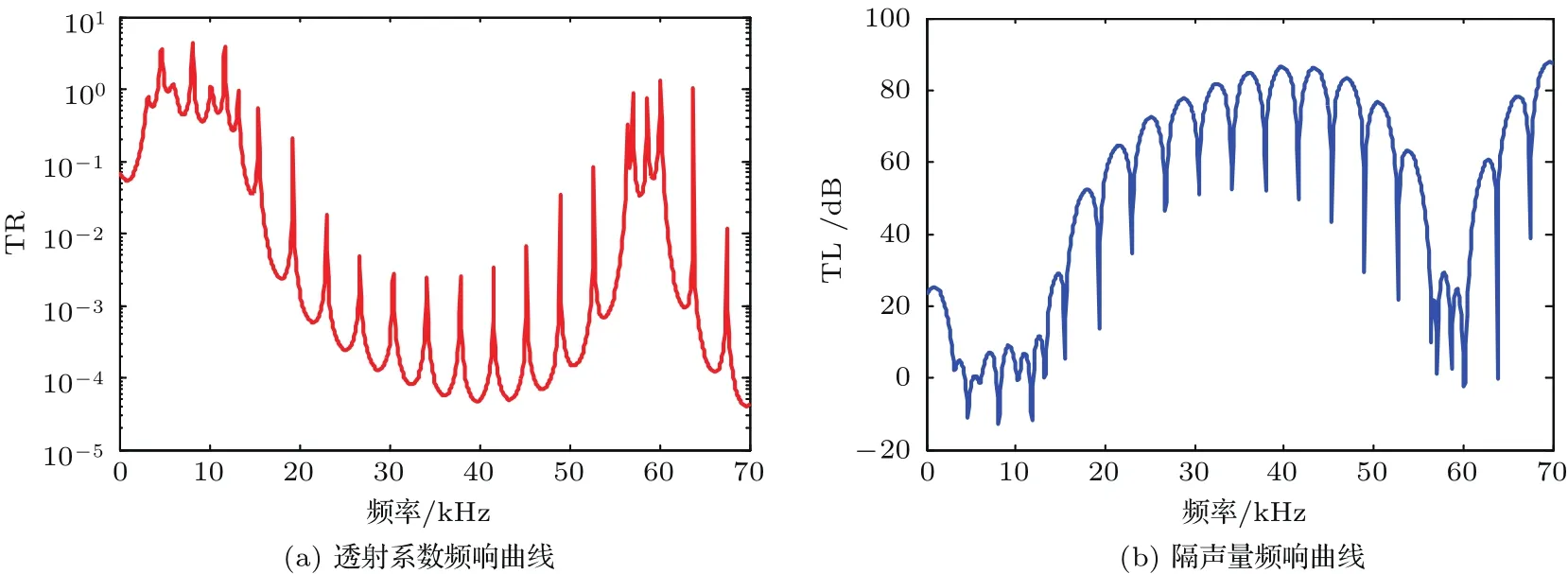
图5 径向声子晶体柱壳的透射系数和隔声量频响曲线Fig.5 Transmission coefficient and sound insulation frequency response curve of cylindrical shell of radial phononic crystal
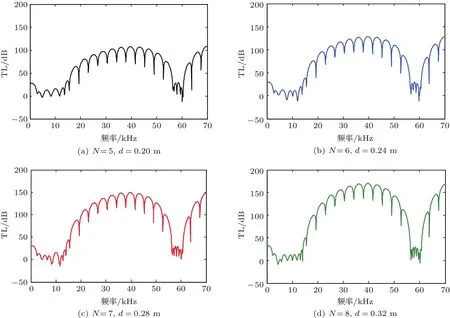
图6 不同周期数下径向声子晶体柱壳的隔声量频响曲线Fig.6 The sound insulation frequency response curve of cylindrical shell of radial phononic crystals in dif f erent cycles
由质量定律可知,增加单一材质壳体的壁厚来提高隔声量并不是一种高效的手段,在第2.1节针对单一材质柱壳隔声性能进行了分析,此处为了便于对比,图6给出了与单质钢柱壳相同厚度的径向声子晶体柱壳的隔声量曲线。可以看到,随着壳体总周期数目N(相当于柱壳的壁厚)的增加,中高频处带隙内的隔声量显著增加,而在0.1 kHz处的隔声量略有增加。由此可见,径向声子晶体柱壳在带隙范围内表现出来的特性突破了声学中质量定律的限制,即可以实现厚度增加一倍,隔声量增加一倍的效果。
2.3 有限元仿真验证
采用COMSOL 5.3声固耦合模块对四周期径向声子晶体柱壳隔声性能进行有限元仿真验证。由于软件不便于拾取径向声子晶体柱壳的隔声量,而可以拾取柱壳内外声场的声压级,其具体数值由声源功率所调控,考虑到仅计算内声场或外声场的声压级曲线并不能体现径向声子晶体柱壳的隔声特性,所以此处针对径向声子晶体柱壳内外声场与结构场接触面的声压级之差进行计算,同时根据式(8)给出数值计算结果,并将两者计算结果进行对比,从而可以验证理论分析的正确性,计算结果如图7所示。

图7 径向声子晶体柱壳的内外声压级之差频响曲线Fig.7 The dif f erence frequency response curve of the inner and outer sound pressure level of cylindrical shell of radial phononic crystals
对比两条频响曲线可知,就带隙位置以及衰减量而言,有限元仿真结果与数值结果几乎完全一致,从而验证了理论分析和数值计算相关结论的正确性。
3 流体介质参数对TL影响规律
隔声量的表达式与内外声场流体介质以及径向声子晶体结构场的本体结构参数有关。目前对于本体结构中材料和结构参数对声子晶体弹性波带隙的影响研究很多,故在本节中,主要针对声场流体介质参数对隔声量的影响进行分析。表3给出了部分常用流体介质的声学常数。
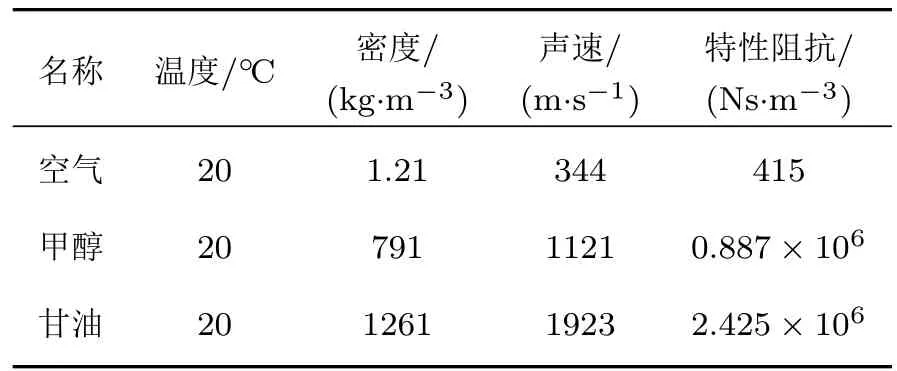
表3 流体介质的声学常数表Table 3 Acoustic constants of the f l uid medium
3.1 内声场流体介质特性阻抗
假定径向声子晶体柱壳的本体结构和外声场流体介质(理想状态下的流体水)固定不变,通过改变内部流体介质的特性阻抗来探索隔声量频响曲线的变化规律。
当内部声场介质的阻抗很小时,隔声量频响曲线峰谷相对较多,随着阻抗的增加,其数量也逐渐减少。图8及图5(b)表现出一个共同点,即声波带隙的位置完全相同,表明声波带隙的位置完全是由径向声子晶体本体结构所调控。
3.2 外声场流体介质特性阻抗
接下来,假定壳体内腔的流体介质为水,径向声子晶体本体结构不变,改变壳体外部声场流体的特性阻抗参数,使外部声场介质的特性阻抗逐渐增大,研究隔声量曲线的变化规律。
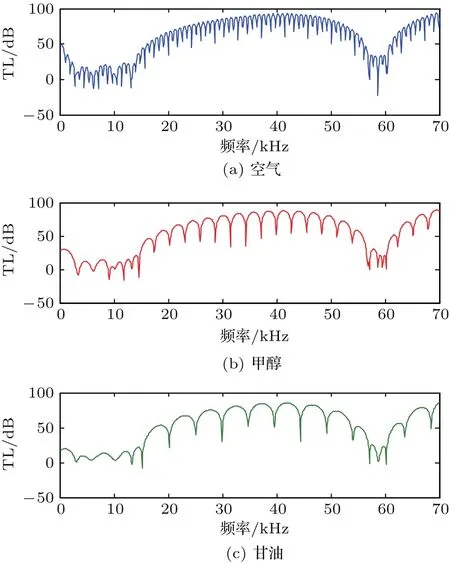
图8 径向声子晶体柱壳内腔流体参数对隔声量的影响Fig.8 The inf l uence of internal f l uid parameters of cylindrical shell of radial phononic crystal on the sound insulation
由图9可以看出,在整个频率区间内曲线的疏密程度几乎是不变的,同时声波带隙的位置也是一致的。然而在图9(a)中,隔声量曲线在带隙范围内 (30 kHz附近处)存在明显的共振峰,而其他曲线并没有出现这一现象,通过进一步分析可知此共振峰位置正对应于表面波模态频率,即出现表面局域态现象。而弹性波带隙内表面局域态现象出现与否,与声子晶体材料的排列顺序有关[22−23]。此处,我们进一步讨论探索声波带隙内表面局域态现象的出现与径向声子晶体材料(软/硬)和内外流体介质(轻/重流体)的排列顺序的关系。通过多组数值计算,得出了表面局域态现象的出现规律,如表4所示。
首先,当内外流体介质采用轻流体排列时,隔声量频响曲线带隙范围定会出现表面局域态现象,相反,采用重流体排列时,则不会出现;当内外流体介质与径向声子晶体组元采用轻/重流体-软/硬材料或重/轻流体-硬/软材料组合排列时,会出现表面局域态现象,相反则不会出现。结果表明,隔声量频响曲线是否会在表面波模态对应频率处出现表面局域态现象,不仅与径向声子晶体柱壳组元材料排列顺序(即自由表面层的波速)有关,同时还受内外声场介质的特性阻抗影响。
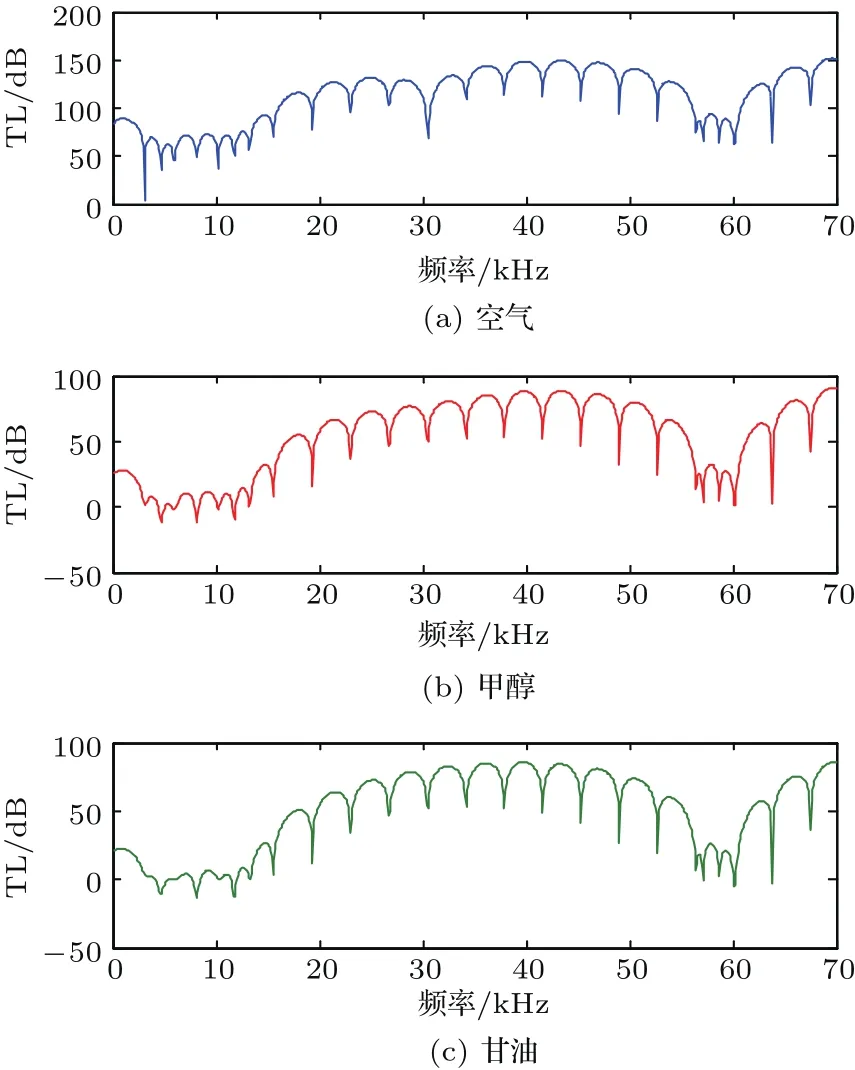
图9 径向声子晶体柱壳外部声场流体参数对隔声量的影响Fig.9 The inf l uence of external acoustic f i eld f l uid parameters of cylindrical shell of radial phononic crystals on the sound insulation
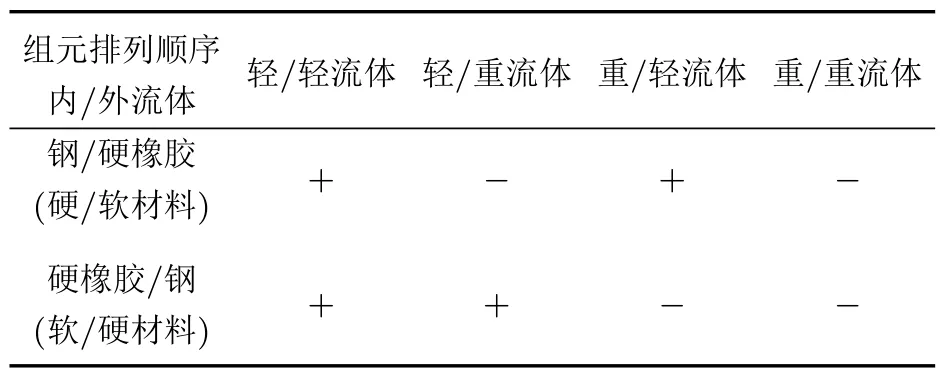
表4 表面局域态现象(+代表存在,−代表不存在)Table 4 The surface localized modes(+represents existence,−represents nonexistence)
4 结论
本文构建了径向声子晶体柱壳的模型。采用力学状态向量传递矩阵法将内外声场与结构场的力学量相结合,系统地研究了在中心线声源激励下声波在径向声子晶体柱壳中的传播特性,并与单一材质柱壳中的传播规律进行对比分析;然后借助有限元方法对数值计算结果进行了验证;最后重点讨论内外声场流体介质对隔声量的影响规律。研究表明:
(1)声波在径向声子晶体柱壳传播过程中,声波带隙的出现能有效地抑制声波由内向外的传播;此外,其在带隙范围内表现出来的隔声特性已经突破声学中的质量定律的限制,当径向声子晶体柱壳的壁厚增加一倍时,带隙范围内的隔声量数值显著增加近一倍。
(2)径向声子晶体内外声场流体参数对隔声量频响曲线峰谷的疏密程度会产生影响,但并不影响声波带隙的位置,带隙的位置是由径向声子晶体本体结构所决定。此外,隔声量频响曲线是否会在表面波模态对应频率处出现表面局域态现象,不仅仅与径向声子晶体柱壳组元材料排列顺序(即自由表面层的波速)有关,同时还要受内外声场介质的特性阻抗的制约,即由内外声场和结构场介质共同决定。
本文的研究对实际工程应用具有一定的指导性,同时也对隔声问题提供一种新的解决途径,拓宽了减振降噪思路。例如,通过合理设计径向声子晶体的材料和结构参数,可以构造出具有不同隔声性能的隔声罩,若进一步结合现有隔声罩原理(如附着各类吸声材料)进行集成,那么极有可能获得性能更为优异的新型隔声罩。
