基于特征值的可验证三方安全密钥交换协议

张艳硕，王泽豪，王志强，陈辉焱

（1.北京电子科技学院密码科学与技术系，北京 100070；2.密码科学技术国家重点实验室，北京 100878；3.数据通信科学技术研究所系统安全部，北京 100191）

1 引言

密钥交换协议是重要的密码机制。利用密钥交换协议，通信双方可以通过一个公开的不安全的信道产生一个秘密的会话密钥，以实现秘密性和数据的完整性。密钥交换协议有着丰富而广泛的实际应用。如TCP/IP中，IPSec安全协议套件中的因特网密钥交换（IKE,Internet key exchange）协议通过建立安全通道、协商安全联盟的方式，建立经过认证的密钥材料[1]。在Web安全中，针对面向上传下发和登录过程的安全防护，应用了以DH（Diffie-Hellman）密钥交换为基础的加密，来代替全面部署安全套接层（SSL,secure sockets layer）的方案[2]。

基于三方的口令认证密钥交换（3PAKE,three-party password authenticated key exchange）允许不安全信道上的2个用户协商安全会话密钥，并通过认证服务器的帮助建立安全信道，以保护其后续通信[3]。现阶段，已有多种不同思路用于设计三方密钥交换协议，如基于混淆设计的三方密钥交换协议[4-5]、基于格的三方密钥交换协议[6]、强三方安全模型下的密钥交换协议[7]和基于口令的三方密钥交换协议[8]等。但许多已提出的协议又被证明存在不同的安全隐患，如Yoon等[9]指出，Wang等[5]提出的协议易受消息修改攻击。Zhao等[10]证明，使用扩展Chebyshev混沌映射的匿名认证协议易受特权攻击和线下密码猜测攻击。模幂运算和对称密钥密码系统的3PAKE协议[11-12]也被证明存在计算成本高、不实用的缺陷。

因此，本文基于特征值方法，构造了一个安全高效的可验证三方密钥交换协议，并给出密钥规模和相关参数。与经典DH协议以及3个不同构造的三方密钥交换协议[6-8]对比后发现，本文所设计的协议具有良好的安全性和高效性，并且给出了基于特征值的设计多方安全密钥交换协议的新方法和新思路。

2 经典密钥交换协议

2.1 DH密钥交换协议

DH密钥交换的思想于1976年在公钥密码学文章《New directions in cryptography》[13]中提出。通信双方Alice和Bob首先协商一个大素数n和g，其中g为n的本原元。n和g不必是秘密的，即他们可以在不安全的途径中进行协商，甚至在一组用户中公用。n和g的选取对安全性有着极大影响。对n的要求是，n必须是一个大素数，且也必须为素数。这是因为系统的安全性依赖于与n长度相同的数的分解难度。g虽然不必是素数，且所有模为n的本原元g都可以被选择，但g必须能产生一个大的模n的乘法组子群。

DH密钥交换过程，Alice选择秘密的XA，计算公开的YA，。Bob选择秘密的XB，计算公开的YB，。Alice把YA发送给Bob，Bob把YB发送给Alice。最后，Alice和Bob协商出的会话密钥为

DH密钥交换将离散对数问题作为困难问题，是最经典的密钥交换协议，可以抵抗公开信道的抗窃听攻击。

2.2 可认证的密钥交换协议

传统的DH密钥交换协议无法抵抗中间人攻击。中间人攻击的原理在于，通信双方Alice和Bob都与中间人用DH算法协商密钥，然后分别用协商好的密钥KA和KB进行通信。中间人在通信双方之间传递信息，这样，通信双方就在不知不觉间泄露了通信内容。

为了抵抗中间人攻击的风险，发展出许多可认证的密钥交换协议[14]，其中最经典的2种为MTI（Matsumoto,Takashima,Imai）密钥协商和STS（station to station）密钥协商。MTI密钥协商[15]能够在2条消息中产生带有抵抗中间人攻击的隐式密钥认证的共享密钥。STS密钥协商[16]是对DH密钥协商的三步交换变体，允许在双方之间建立一个共享密钥，并带有相互实体认证和相互显示密钥认证。STS密钥交换协议可以起到抵抗中间人攻击的作用，使通信双方可以确信在网络中只有合法的用户可以计算出密钥。

MTI密钥交换无法提供实体认证，也不能进行密钥确认，因此，其只能用于被动攻击情景中。STS密钥交换用于被动攻击和主动攻击的情景中的安全性都没得到证明。这2种协议都存在一定的安全缺陷。

3 基于特征值的三方安全密钥交换协议

3.1 特征值简介

特征值定义如下。

定义1[17]设A是n阶矩阵，E为单位矩阵，如果数λ和n维非零列向量x使式(1)成立，那么，这样的数λ称为矩阵A的特征值，非零向量x称为A的对应于特征值λ的特征向量。

式(1)也可写成

式(2)是n个未知数n个方程的齐次线性方程组。

3.2 三方密钥交换协议

本节方案基于矩阵特征值进行构造，通信三方可以确保只有合法用户才能计算出会话密钥。具体方案如下。

设密钥交换的三方分别为Alice、Bob和Carol。选择一个秘密n阶矩阵A。设A的特征值λi(1≤i≤n)所对应的特征向量为pi(1≤i≤n)。具体步骤介绍如下。

Step1用户Alice随机选择A的一个特征向量pa，其中1≤a≤n，将pa传给Bob和Carol。

Step2用户Bob随机选择A的一个特征向量pb，其中1≤b≤n，将pb传给Alice和Carol。

Step3用户Carol随机选择A的一个特征向量pc，其中1≤c≤n，将pc传给Alice和Bob。

Step4用户Alice、Bob、Carol根据式(1)由pa、pb、pc计算λa、λb、λc，得出会话密钥λa+λb+λc。

对于该密钥交换协议，由于攻击方无法掌握秘密矩阵A，故其无法伪造会话密钥进行常规的中间人攻击。

但是可以证明，如果存在攻击方C，且C掌握秘密矩阵A的所有特征向量pi(1≤i≤n)，那么C就可以从中任选3个特征向量分别发送给Alice、Bob和Carol。这样Alice、Bob和Carol等合法用户便会建立起错误的会话密钥，从而该次密钥协商被C所破坏。

3.3 可验证的三方密钥交换协议

针对上述安全漏洞，本文借鉴3.2节三方用户交换矩阵特征向量的思路，在其基础上，利用矩阵特征值的重根特性，对秘密矩阵的构造进一步限定，构造一个添加了用户身份验证功能的密钥交换协议。

首先，构造一个2n阶秘密矩阵A，该矩阵满足如下要求。

1)所有特征值λi(1≤i≤n)均为二重根，即有n个不同的λ。

2)矩阵A相似于对角阵。

矩阵A为以下方案中3个合法通信方共同保有的信息，即A可被视为密钥。

合法用户共享一个满足上述要求的2n阶秘密矩阵A，并设A的每个特征值λi(1≤i≤n)所对应的2个特征向量为和(1≤i≤n)。设通信三方为Alice、Bob和Carol。方案过程介绍如下。

Step1Alice随机选择特征向量对发送pa给Bob和Carol。

Step2Bob随机选择特征向量对发送pb给Alice和Carol。

Step4用户Alice收到pb和pc之后，首先进行合法性验证，即判断pb、pc包含的特征向量是否成对。验证通过后，根据式(1)通过秘密矩阵A由pa计算出λa，由pb计算出λb，由pc计算出λc，计算会话密钥Kabc=λa+λb+λc。

Step5用户Bob收到pa和pc后，首先进行合法性验证，即判断pa、pc包含的特征向量是否成对。验证通过后，根据式(1)通过秘密矩阵A由pa计算出λa，由pb计算出λb，由pc计算出λc，计算会话密钥Kabc=λa+λb+λc。

Step6用户Carol收到pa和pb之后，首先进行合法性验证，即判断pa、pb包含的特征向量是否成对。验证通过后，根据式(1)通过秘密矩阵A由pa计算出λa，由pb计算出λb，由pc计算出λc，计算会话密钥Kabc=λa+λb+λc。

4 安全性分析

4.1 矩阵构造与合法性认证

首先，由于3.3节的密钥交换协议是基于3.2节所述密钥交换协议而构造的，故其可以抵御传统的中间人伪造会话密钥，窃听合法用户通信的攻击。同时，该协议还可以抵御3.2节所述的中间人对密钥协商过程的干预，即避免攻击方C使3个合法通信方误以为自己与对方建立起会话密钥这种安全漏洞。

定理1矩阵A相似于对角阵的充要条件为，A有n个线性无关的特征向量。

由于选取的2n阶秘密矩阵A相似于对角阵，由定理1可知，A有2n个线性无关的特征向量。又由于所构造的A的特征值均为二重，因此A的每个特征值都有2个特征向量。

方案的合法性认证正是基于这种秘密矩阵的特殊构造的。通信方在接收到另两方的特征向量对时，验证特征向量是否成对是保证通信方身份是否合法的一个关键步骤。如果出现特征向量不成对的情况，便认为对方身份合法性存疑，认证不通过。

4.2 密钥量计算

为了防止攻击方对秘密矩阵A的穷举攻击，需要对密钥量进行估计，即计算A有多少种选择。

设方案基于有限域Zq，按照3.3节的矩阵设计要求，对于同2n阶矩阵A相似的对角阵Λ而言，其每个对角元素有q种取值，又因为需保证n个特征值两两不同，故Λ所有的特征值组合方案个数Nc为

其中，q>n。因此，可得出Λ所有的特征值排列方案个数Np为

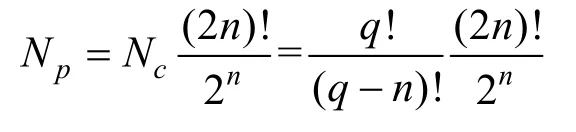
又因为P为可逆矩阵，有定理2成立。

定理2若A为可逆矩阵，则矩阵乘法AB=AC或BA=CA满足消去律。

因为方案中P为可逆矩阵，因此根据定理2有PΛ1P-1≠PΛ2P-1。这意味着不同的对角阵一定对应着不同的秘密矩阵A。即对于固定的一个P，可以生成Np个不同的A，方案密钥量为Np。

4.3 复杂性分析

假设Alice、Bob和Carol为合法的通信用户，攻击方C若要对通信进行破坏，要进行两步攻击，首先需要得到密钥，即矩阵A。根据4.2节的密钥量计算，可知C掌握正确密钥的概率为。

若要伪造其中的一个合法用户发送信息，就需要从全部特征向量中选取2个成对的发送出去。假设矩阵的阶为2n，则C成功的选取到成对特征向量的概率为

当q的远大于n时，C成功对通信进行破坏的概率为

可以看出，攻击成功的复杂度非常高，攻击成功的概率小到几乎可以忽略不计，攻击方对通信进行破坏的概率极低，这意味着攻击方对密钥协商过程进行干预的成功率将非常小，很难通过合法一方的合法性验证。

5 协议性能比较

本节将本文设计的密钥交换协议与传统的DH协议、基于格的密钥交换协议[6]、强三方安全模型下的密钥交换协议[7]、基于口令的密钥交换协议[8]进行比较。各类密钥交换协议性能比较如表1所示，其中，Type表示协议类型，Mutu-Auth表示协议是否提供双向认证的功能，Round表示协议所需的轮数。

表1 各类密钥交换协议性能比较

从表1中可以看出，本文提出的三方交换协议支持双向认证，具有安全性上的优势。在效率方面，本文在基于秘密矩阵的前提下，实现了只需一轮即可达到可验证密钥交换的目的，效率更高。

在本文涉及的密钥量方面，根据4.2节的数据和4.3节对复杂性的分析可知，密钥量Np可规约为阶乘运算，密钥空间足够大，可以保证协议的安全性。

在计算复杂性方面，密钥交换要保证在基本的多项式时间内无法进行有效攻击。传统的DH密钥交换协议基于离散对数问题进行设计，是典型的NP问题。文献[6]所提的基于格的密钥交换最终被规约为SVP（shortest vector problem）问题，是NP完全问题。文献[7]的密钥交换被证明为包含密钥确认的认证密钥交换协议（AKC,authenticated key exchange protocol with key confirmation）安全，其复杂性可阐述为多项式时间内，攻击者成功猜出输出为会话密钥还是随机数的概率可忽略。文献[8]所提的3PAKE协议被证明在随机预言机模型下，基于计算DH困难性假设是安全的。本文所提方案在4.3节中被证明其计算复杂性为阶乘级，这意味着多项式时间内中间人攻击成功的概率可忽略，满足了密钥交换协议的基本设计要求。

6 三方密钥交换协议举例

6.1 基于特征值的三方密钥交换协议举例

设通信三方为Alice、Bob和Carol。在有限域Z11上构造秘密矩阵，可计算得到A的3个特征值为λ1=2，λ2=8，λ3=10，其对应的特征向量依次为p1=(0,1,0)，p2=(1,1,0)，p3=(1,1,1)。具体步骤介绍如下。

Step1用户Alice随机选择A的一个特征向量pa=(0,1,0)，将其传给Bob和Carol。

Step2用户Bob随机选择A的一个特征向量pb=(1,1,1)，将其传给Alice和Carol。

Step3用户Carol随机选择A的一个特征向量pc=(1,1,0)，将其传给Alice和Bob。

Step4用户Alice、Bob和Carol都根据式(1)，由pa、pb、pc计算得到λa=2，λb=10，λc=8，得出会话密钥Kab=λa+λb+λc=20。

6.2 基于特征值可验证的三方密钥交换协议举例

为了方便演示且限于篇幅，本文选取秘密矩阵为4阶矩阵，但实际应用中需要一个远大于该阶数的矩阵。秘密矩阵的构造方法可以通过先设定特征值和特征向量，再以此倒推出秘密矩阵的方式进行。

按照3.3节所述的矩阵构造要求，在有限域Z11上构造秘密矩阵为

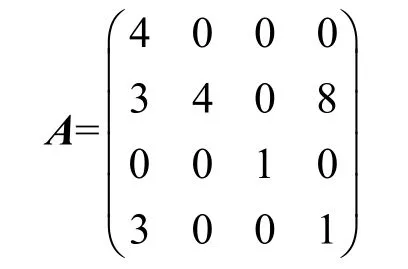
因为存在可逆矩阵P，使

设通信三方为Alice、Bob、Carol，方案过程如下。

1)用户Alice随机选取特征向量对pa=((0,1,1,1)T,(0,1,0,1)T)。

2)用户Bob随机选取特征向量对pb=((0,1,0,0)T,(1,1,0,1)T)。

3)用户Carol随机选取特征向量对pc=((0,1,0,0)T,(1,1,0,1)T)。

4)合法用户在获得另两方发来的特征向量对之后，首先进行合法性验证，即判断特征向量是否成对。验证通过后，根据式(1)由秘密矩阵A计算得到λa=1，λb=4，λc=4。计算会话密钥为

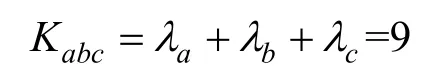
7 结束语

本文在基于矩阵特征值的思路之上，首先提出一种简单的三方密钥交换协议。该协议可以抵抗中间人攻击，但无法抵御中间人对密钥交换过程的干预。针对这一问题，本文对秘密矩阵进行限制，基于二重特征值提出了一种既可抵御中间人攻击，又可以进行用户合法性认证的三方密钥交换协议。对比分析证明，该协议具有良好的安全性和高效性。同时，该协议每次都可以重新协商新的会话密钥，防止一个密钥多次使用带来的安全隐患，具有很好的灵活性，为三方或多方密钥交换协议设计提供了一种新方法和新思路。