基于张量填补和用户偏好的联合推荐算法
2019-04-01熊智徐恺蔡玲如蔡伟鸿
熊智,徐恺,蔡玲如,蔡伟鸿
(1.汕头大学计算机科学与技术系,广东 汕头 515063;2.汕头大学智能制造技术教育部重点实验室,广东 汕头 515063)
1 引言
随着计算机技术的发展与应用,越来越多的用户通过网络获取信息,使互联网上的数据呈爆发式增长趋势。如何在“信息超载”的时代为用户进行精准推荐是目前众多学者所关注的问题。推荐系统能够根据用户喜好过滤冗余的信息进而为用户自动推荐[1]。推荐系统使用户能够更加快速地获取自己感兴趣的信息,节省用户的时间成本,增强产品的用户体验。近年来,推荐系统得到了广泛应用,推荐算法的种类也越来越多样化[1-2]。
目前,主流的推荐算法主要包括基于协同过滤的推荐算法[3-5]、基于矩阵分解的推荐算法[6-7]、基于关系网络的推荐算法[8]、基于机器学习的推荐算法[9-11]和混合推荐算法[12]等。基于协同过滤的推荐算法和基于矩阵分解的推荐算法往往只构建用户和项目之间的评分矩阵,根据相似用户进行推荐。基于关系网络的推荐算法挖掘用户与用户、项目与项目之间更深层次的联系,利用图或网的形式进行推荐,它与基于机器学习的推荐算法一样,当用户及项目数量较大时,算法的计算量较大,因此通常需要高性能硬件环境的支撑。在一个实际的推荐系统中,所能获得的数据除了用户对项目的评分,通常还包含项目的分类情况,例如,小说可以分成科幻、历史等类别,电影可以分为喜剧、战争、动画等类别。如果能很好地利用项目的类别信息,将有助于提升推荐质量。然而,上述推荐算法仅依据评分数据进行推荐,忽略了项目的类别信息。
张量是矢量概念和矩阵概念的推广,它可以表示更高维度的数据。近些年来,有些研究开始引入评分数据之外的信息构建三维张量,例如类别信息和时间信息等,进而设计推荐算法。相对于二维的评分数据,考虑了其他维度信息的三维张量更加稀疏和复杂。文献[13]在电影推荐中将用户−电影−类别组成的三维张量拆分为用户−电影、电影−类别的双边关系,然后使用矩阵分解等算法进行处理并推荐。文献[14]构建用户−项目−时间的三维张量,提出一种基于审美的衣服推荐算法,但是也将三维张量转化成多个二维矩阵进行处理,虽然考虑了三维的数据信息,但丢失了数据之间整体的联系性。文献[15]构建用户−标签−项目的三维张量用于标签推荐,利用低阶多项式改进了用户、项目和标签之间的统计信息,同时解决了数据稀疏性问题。尽管其相对于经典的CP(CANDECOMP/PARAFAC)分解和Tuker分解[16]在时间和空间的复杂性上都有所改善,但是计算成本依然相对较高,因而只能用于小规模的三维张量。文献[17]利用高阶奇异值分解(HOSVD,high order singular value decomposition)进行音乐推荐。并通过音乐之间的相似性来解决数据稀疏性问题。文献[18]在标签推荐上采用了与文献[17]类似的方式,但这2种方法都没有采用迭代处理提升准确度。
在一些大型系统中,项目和用户的数量都很庞大,而用户评分过的项目通常很少,2个用户共同评分过的项目更少,解决数据稀疏问题是提高推荐质量的关键。张量填补是解决数据稀疏性的一种常用方法。文献[19]通过张量因式分解的形式填补张量中的缺失值,但它只适用于N×N×N的张量。文献[20]提出利用黎曼流形和非线性梯度下降的方式来填补张量中的缺失值,虽然能处理更高维度的数据,但要求张量的秩已知或者可以被测量。
推荐算法要向用户推荐其喜欢的项目,也就是说要“投其所好”。如果能从已有的数据中分析挖掘用户的偏好信息,并在推荐算法中加以应用,将会使推荐更加切合用户的需求,有助于提高推荐效果[21]。因此,本文综合考虑用户的项目类别偏好和评分偏好,提出了一种基于张量填补和用户偏好的联合推荐(TCUP,tensor completion and user preference)算法。首先,基于评分矩阵和项目所属类别矩阵构建用户−项目−类别的三维张量;然后,利用Frank-Wolfe算法进行迭代计算,填补张量中的缺失数据,同时基于张量数据构建用户类别偏好矩阵和评分偏好矩阵;最后,基于填补后的三维张量以及2个偏好矩阵设计了联合推荐算法,并采用差分进化算法进行参数调优。为了验证TCUP算法的有效性,本文使用MovieLens[22]数据集进行测试。在4种不同规模数据集下的实验结果表明,TCUP算法的数据填补效果和推荐效果优于一些常用和新近提出的算法。
2 相关知识
2.1 张量的相关符号及计算式
本文中,向量和矩阵分别用小写和大写的加粗字母表示,张量用加粗的花体字母表示。文中涉及的相关符号和计算式如下。

A
为了便于理解张量的矩阵化和矩阵的张量化,下面给出一个三阶张量的示例(文中所述张量皆为三阶张量)。假设X为图1所示的3×4×2的张量,即X∈R3×4×2。

图1 张量示例
那么,张量X的矩阵化可表示为如式(1)~式(3)所示的形式。


2.2 FW算法
FW(Frank-Wolfe)算法是一种求解受限(带约束)凸优化问题的方法。它采用迭代计算的方式,将非线性优化问题转换成一系列线性优化问题进行求解。FW算法能够应用于矩阵分解,并能保证较好的收敛性[23]。假设有优化问题,其中,f(x)是连续可微的凸函数,D为凸形紧集,即在集合D内最小化f(x)的值。FW算法求解该问题的流程如算法1所示。
算法1Frank-Wolfe算法
1)设置最大迭代次数T。
2)初始化一个解x(0),当前迭代次数t=0。
5)进行一次迭代,x(t+1)=x(t)+γ(t+1)⋅(s(t+1)-x(t))。
6)更新当前迭代次数,t=t+1。
7)当前迭代次数t是否达到最大迭代次数T,若是则停止迭代并输出x(t),否则重复步骤3)~步骤6)。
3 联合推荐算法
基于张量填补和用户偏好的联合推荐算法包括以下4个步骤:张量构建、张量填补、偏好构建和联合推荐,如图2所示。下面分别介绍这4个步骤。

图2 联合推荐算法的步骤
3.1 张量构建
根据用户对项目的评分数据和项目所属的类别数据可分别构建矩阵M和N。矩阵M中记录用户对项目的评分,如果某个用户对某个项目有评分,则对应的元素为该评分值,否则为0。矩阵N记录项目所属的类别,如果某个项目属于某个类别,则对应的元素为1,否则为0。一个项目可以属于多个类别。
根据矩阵M和N可构建2个三维张量A和B如式(4)和式(5)所示。

其中,u、i和c分别表示用户、项目和类别的坐标。此外,本文用U、I和C分别表示用户、项目和类别的数量。
3.2 张量填补
张量A通常非常稀疏,本文利用张量填补的方式来填补其中缺失的数据。对于已知的D(这里D=3)维张量A,假设令A中元素不为0的坐标构成的集合为Ω,其张量填补可表述成如下优化问题:寻找一个与A规模相同的张量X,使
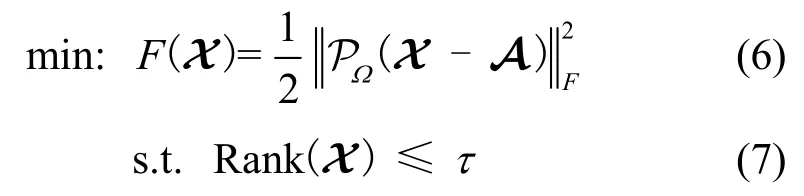
其中,PΩ(X-A)是一个张量,当(i1,i2,…iD)∈Ω时,,否则。该张量填补问题即为,找一个秩不超过τ的张量X,使在Ω范围内X同A尽可能接近。
在矩阵填补中,核范数(nuclear norm)常用来替代矩阵的秩。对于张量,也有一些核范数,例如overlapped核范数[24]和scaled-latent核范数[25]等,而scaled-latent核范数在低秩张量填补中优于overlapped核范数[26]。因此本文用scaled-latent核范数来代替张量的秩。
X的scaled-latent核范数定义为

式(8)表示将X拆解成D个张量的和(D为X的维度),要找到一种拆解方式使最小,该最小值即为X的scaled-latent核范数。那么,可以将式(7)替换成

下面采用FW算法求解由式(6)和式(9)构成的优化问题。根据式(6),FW算法中的步骤3)可写为

虽然式(10)是一个线性优化问题,但由于scaled-latent核范数的定义较为复杂,因而式(10)中的约束较为复杂,很难求得式(10)的最优解,因此本文采用如下方法求其次优解:首先构造一批满足约束条件的可行解,然后从这些可行解中挑选最优解。


其中,σk>0为奇异值,uk和vk为对应的左右奇异(列)向量。由于左奇异向量之间两两正交,右奇异向量之间两两正交,则
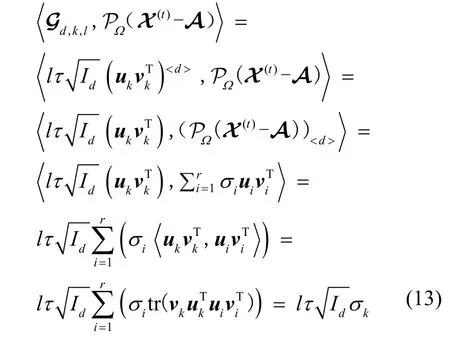
由于式(10)要求最小值,根据式(13)可知,S(t+1)为所构造的张量Gg,k,l中使最小的那个,其l等于–1,σk为(PΩ(X(t)-A))

另外,根据上面的求解过程可知,采用FW算法进行张量填补的计算开销较小。
3.3 偏好构建
一般的推荐算法都是直接依据张量(或矩阵)填补后的数据进行推荐,然而本文认为,张量填补虽然能够填补缺失的数据,但并不能就此做出推荐,因为张量填补没有很好地考虑到用户的偏好信息。以书籍推荐为例,如果某用户从未接触过历史类型的书籍,但在填补后的张量中,可能由于有一些与他相似的用户给历史类型书籍评了高分,导致某些历史类型的书籍被该用户评了高分(不是该用户进行的评分,而是被填补的)而被推荐,因此需要考虑用户的类别偏好。如果某用户特别偏爱历史类型的书籍,对历史类型书籍的评分明显高于其他用户,那么有可能因为其他用户对历史类型书籍的评分过低,导致历史类型的书籍被该用户评分(不是该用户进行的评分,而是被填补的)过低而不被推荐,因此需要考虑用户的评分偏好。所以,在推荐中加入用户的类别偏好和评分偏好将有助于提升推荐质量。
根据张量A和B构建用户的类别偏好矩阵P和评分偏好矩阵Q。用户u对类别c的偏好定义为,用户u对类别c项目的评分次数除以用户u对所有类别项目的总评分次数,其计算方法为

用户u对类别c的评分偏好定义为,用户u对类别c项目的平均评分减去其他用户对类别c项目的平均评分,其计算方法为
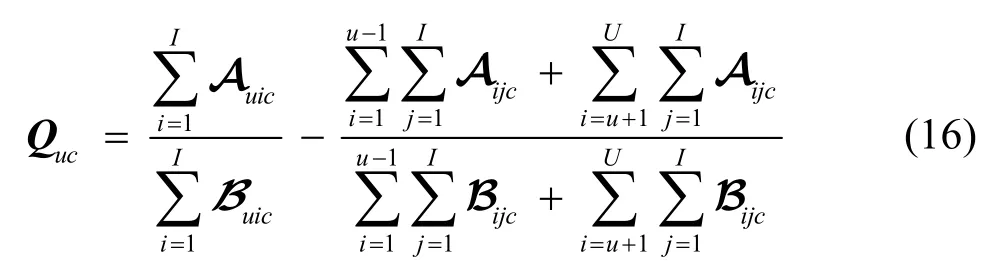
用户的类别偏好矩阵P和评分偏好矩阵Q分别表示为

3.4 联合推荐
假设张量A填补后的张量为A'。为了进行最后的推荐,需要根据三维张量'A,以及类别偏好矩阵P和评分偏好矩阵Q计算得到U行I列的推荐矩阵O,矩阵O的元素表示各个项目对各个用户的推荐程度。下面给出矩阵O的计算方法。
在张量A'中,用户u和项目i对应一个类别向量;在矩阵P和Q中,用户u分别对应向量Pu*和Qu*;这3个向量的长度均为C。本文根据这3个向量来计算Oui的值(注意,如果用户u已经对项目i评过分,则不需要计算Oui的值),计算方法如图3所示。首先对3个向量进行加权求和得到一个向量,然后取该向量的最大元素作为最终Oui的值。

图3 推荐程度值的计算
本文采用差分进化算法来确定w=(wp,wq)的最优值。差分进化算法是基于种群的全局优化方法,包括变异、交叉和选择3种基本操作[27]。详细步骤如算法2所示,其中w为个体,个体的适应度函数为以该个体为权重时的推荐精度(精度的定义参见4.2节)。
算法2求最优权重的差分进化算法
1)设置种群大小NP、最大迭代次数G、缩放因子F和交叉概率CR。
2)随机产生初始种群中的个体wi,i=1,2,…,NP,当前代数g=0。
3)变异。种群内个体的差分向量经过缩放与种群内相异的个体相加产生变异个体vi=wa+F(wbwc),i≠a≠b≠c。
4)交叉。变异个体和原个体进行交叉,产生试验个体ui:如果rand(0,1)≤CR,那么ui,j=vi,j,否则ui,j=wi,j,j表示个体的分量,且保证ui至少包含变异个体vi的一个分量。
5)选择。挑选原个体wi和试验个体ui中适应度函数值大的那个作为新的个体wi进入下一代种群,更新当前代数g=g+1。
6)如果g=G,则停止迭代并输出种群中的最优个体;否则重复步骤3)~步骤5)。
4 实验结果及分析
4.1 数据集及实验环境
实验所用的数据来源于MovieLens[22]上最新的数据集,数据集中评分的范围为0.5~5(包含0.5分和5分),且为0.5的倍数。为了验证不同数据规模对实验结果的影响,本文使用4种不同规模的数据集进行测试,各数据集的相关信息如表1所示。
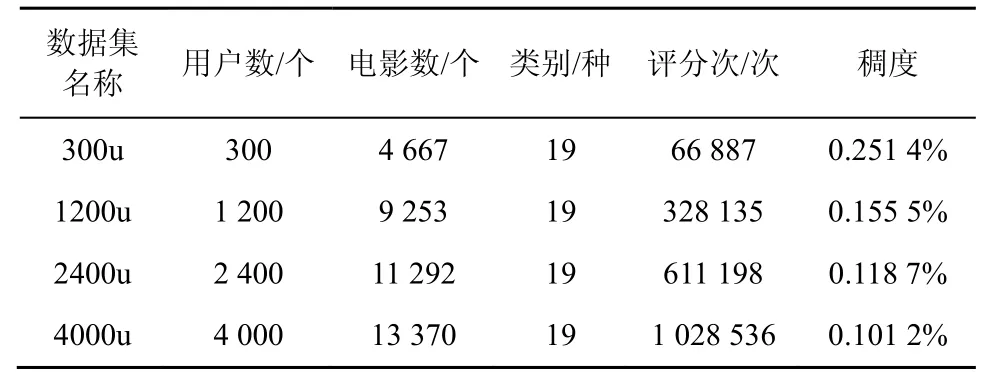
表1 4种不同规模的数据集
每个数据集被随机分成80%的训练集和20%的测试集。实验在配置为Intel Core i7 3.40 GHz CPU、24 GB内存的Windows 7 PC机上进行,运行环境为Matlab R2014a。
4.2 评价指标
从误差和准确性两方面来评测推荐算法的性能。评价误差的性能指标包括平均绝对误差(MAE,mean absolute error)和均方根误差(RMSE,root mean square error),用来衡量在测试集中张量填补值与真实值之间的误差,计算方法如下。

TP:项目推荐给用户,且事实上用户也对项目评过分。
TN:项目未推荐给用户,且事实上用户未对项目评过分。
FP:项目推荐给用户,但事实上用户未对项目评过分。
FN:项目未推荐给用户,但事实上用户对项目评过分。

4.3 对比算法及参数测定
本文将提出的基于张量填补和用户偏好的联合推荐算法TCUP与4种典型的以及2种新近的推荐算法进行对比测试,对比算法及其用到的主要相关参数如表2所示。
由于LRML算法没有依据具体的评分值进行推荐,而只是将条目(用户,项目)标记为0或1,分别表示用户是否对该项目评过分,因此对于该算法本文不进行填补误差的分析,而只进行推荐准确性的分析。结合文献[3,6,9-11,17,20]中的参数设置,以及文献[7]中对比测试时的参数设置,并通过多次实验为各算法选择最优参数,结果如表3所示。在测试TCUP算法中的最优权重wp和wq时,计算的是top@10下的最优权重,并以此权重作为其他top@N推荐的权重。差分进化算法的参数如下:种群大小NP为20,缩放因子F为0.2,交叉概率为CR为0.9,最大进化代数G为20。以下所有测试均是在最优参数下进行的。
4.4 张量填补的误差分析
误差分析是用来评测各算法填补得到的评分值与测试集中真实值的偏差情况,结果如表4所示。由表4中的结果可知,在300u数据集下,ALS算法表现最差,SVD++算法表现最好。在其他更大规模的数据集下,HOSVD算法的误差明显高于其他算法;SVD++、Precon和TCUP算法表现较好,误差明显低于其他3种算法,其中TCUP算法略优于SVD++和Precon算法。从总体上来看,TCUP算法的综合表现最优,尤其是当应用于较大规模的数据集时。

表2 对比算法及相关参数
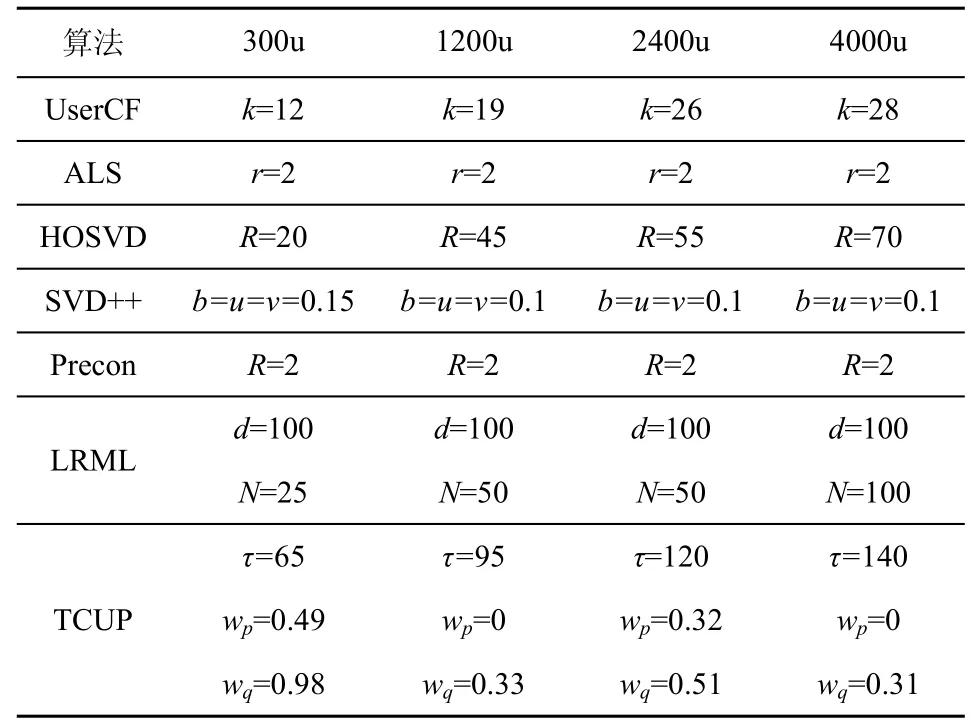
表3 不同算法的参数设置
4.5 推荐算法的准确性分析
图4和图5分别展示了不同数据集下各算法的精度和召回率的对比,其中top@N表示向每个用户推荐项目的数量。图4的结果表明,TCUP算法表现最佳,其推荐精度在不同数据集下均明显高于其他算法;LRML算法的性能次之,精度可以保持一个较好的水平;UserCF、ALS、SVD++和Precon算法的精度则基本一直处于较低水平。相对于LRML算法,在300u数据集下推荐时,TCUP算法的精度平均提升幅度最小,为1.96%;在4000u数据集下进行推荐时,TCUP算法的精度平均提升幅度最大,为3.44%。

表4 误差分析比较

图4 不同数据集下各算法的精度对比

图5 不同数据集下各算法的召回率对比
从图5可以看出,所有算法的召回率均随着top@N的增大而增大,这是因为随着推荐数量的增加,推荐给用户且用户评过分(即看过)的电影数量也在增加,而用户评过分(即看过)的电影数量保持不变。TCUP算法表现最好,LRML算法的性能略低于TCUP;UserCF、ALS、SVD++和Precon算法的召回率则一直处于较低水平,性能较差。相对于LRML算法,在1200u数据集下进行推荐时,TCUP算法的召回率平均提升幅度最小,为1.35%;在300u数据集下进行推荐时,TCUP算法的召回率平均提升幅度最大,为2.40%。
表5~表8分别给出了不同数据集下各算法的负正率、F1分数和准确率。结果表明,所有算法的负正率都较低,这是因为评分非常稀疏,而且top@N也较小,所以大量的元素都属于“项目未推荐给用户,且事实上用户也未对项目评过分”,即TN非常大,由式(23)可知负正率会非常小。在部分测试中由于保留小数位数的原因,有些算法的负正率会相同。但总体上TCUP算法的负正率相比于其他算法较低,性能最优。在F1分数的测试中,TCUP算法表现一直最优,这是因为它的精度和召回率相比其他算法都有优势。另外,所有算法的准确率都在97%以上,这是因为TN非常大,由式(23)可知准确率会比较接近1。但相对而言,TCUP算法的准确率一直都是最高的。

表5 300u下不同算法的性能对比

表6 1200u下不同算法的性能对比

表7 2400u下不同算法的性能对比

表8 4000u下不同算法的性能对比
整个实验结果表明,相对于其他6种算法,TCUP算法呈现较低的误差,在精度、召回率、负正率、F1分数,以及准确率上都有较明显的优势,因此,本文提出的TCUP算法能取得更好的推荐效果。
5 结束语
本文提出了一种联合张量填补和用户偏好的推荐算法TCUP。该算法首先基于评分矩阵和项目所属类别矩阵构建用户–项目–类别的三维张量。然后,将三维张量的填补描述成带约束的非线性优化问题,并借助scaled-latent核范数来代替对张量秩的约束,接着利用Frank-Wolfe算法将非线性优化问题转换成一系列线性优化问题进行求解,并为scaled-latent核范数约束下的线性优化问题给出了一种计算量较小的求解方案。最后,基于张量数据构建用户类别偏好矩阵和评分偏好矩阵,联合填补后的张量和2个偏好矩阵设计了推荐算法,并采用差分进化算法进行参数调优。实验结果表明,相对于其他6种推荐算法,TCUP算法在误差分析上呈现一个较低的误差;在准确性分析上其精度和召回率等指标均有明显优势,其中,精度的平均提升幅度为1.96%~3.44%,召回率的平均提升幅度为1.35%~2.40%。由于高维张量各维度的重要程度不同,如何更好地考虑各维度的差别是接下来的研究方向。
