周期为p2的q元序列的k–错线性复杂度
2019-04-01吴晨煌许春香杜小妮
吴晨煌,许春香,杜小妮
(1.电子科技大学计算机科学与工程学院,四川 成都 611731;2.莆田学院应用数学福建省高校重点实验室,福建 莆田 351100;3.西北师范大学数学与统计学院,甘肃 兰州 730070)
1 引言
伪随机序列的应用领域非常广泛,在通信、雷达导航、密码学等领域都有极其重要的应用。比如在流密码中,伪随机序列作为密钥序列与明文序列进行按位异或运算得到密文序列,因此,流密码的安全性完全基于密钥序列的密码学指标。线性复杂度是伪随机序列的一个很重要的密码学指标,其刻画使用线性移位寄存器生成该序列所需线性移位寄存器的最小阶。线性复杂度[1]的计算方法介绍如下。
设有限域Fq={0,1,2,…,q-1},q为素数。设(un)n≥0=(u0,u1,…,uT-1,…)为Fq上最小周期为T的q元序列(下文中所指的周期均为最小正周期),其线性复杂度为(un)n≥0,满足Fq上的如下线性递归关系的最小阶,即
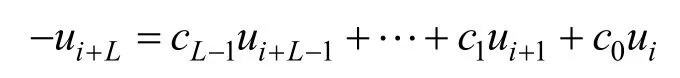
其中,i≥0,c0≠0,c1,…,cL-1∈Fq。把最小阶对应的多项式
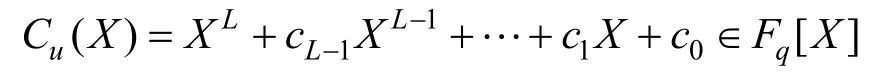
称为序列(un)n≥0的极小多项式。记(un)n≥0的生成多项式为
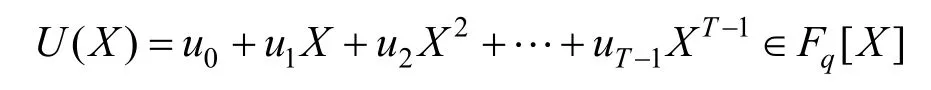
则(un)n≥0在Fq上的线性复杂度可通过式(1)[2]计算得到。
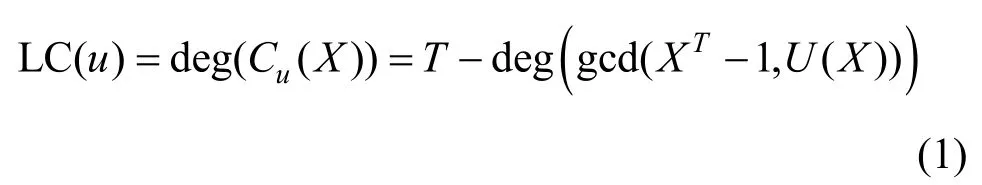
即(un)n≥0的线性复杂度恰好为(un)n≥0的极小多项式的次数。
但是,一个线性复杂度高的序列未必具有好的稳定性,比如周期为T的二元序列000…0001,其线性复杂度为T-1,但是当该序列改变一位之后即为全0序列,其线性复杂度降为0。为此,Stamp等[3]引入了k-错线性复杂度的概念来衡量序列的稳定性,即当序列在至多改变k位之后其线性复杂度的最小值。k-错线性复杂度是在重量复杂度[4]的基础上给出的,或更早之前Ding等[5]也称之为球体复杂度。因此,在密码学应用中,序列的线性复杂度不仅要大,而且在序列改变若干位之后其线性复杂度不应显著降低,即稳定性要好[5-6]。
在计算序列的线性复杂度的算法研究方面,Berlekamp[7]和Massey[8]分别设计了计算周期序列或有限序列线性复杂度的算法,即广为人知的BM(Berlekamp-Massey)算法。之后,Games等[9]给出了一个计算周期为2n的二元序列线性复杂度的快速算法即Games-Chan算法,该算法的时间复杂度比BM算法小很多。1993年,Stamp等[3]在Games-Chan算法的基础上,通过引入一维代价数组,给出了计算周期为2n的二元序列k-错线性复杂度的快速算法。Meidl[10]进一步讨论了周期为2n的二元序列的稳定性。
对于周期为pn的二元序列(p为奇素数),1999年,魏仕民等[11]扩展了Games-Chan算法,提出了一个计算周期为pn的二元序列的线性复杂度的快速算法。该算法是一个迭代计算的方法,其思想如下。把周期为pn的二元序列(s)按照行为主序排列为一个p×pn-1矩阵,若该矩阵的每一行都相同,则记λ=1,否则λ=0。然后把每一行相加得到一个周期为pn-1的新序列(s'),得到这2个序列线性复杂度的一个关系式:LC(s)=LC(s')+λ(p-1)pn-1。以此类推,最后求出二元序列(s)的线性复杂度。2001年,王磊等[12]基于Stamp-Martin算法[10]的思想,对文献[11]的算法进行了扩展,给出了一个计算周期为pn的二元序列的k-错线性复杂度的效率更高的算法。需要说明的是,在文献[11-12]中都要求2为模pn的本原元。最近,陈智雄等[13]给出了一个计算周期为p2的二元序列的k-错线性复杂度的快速算法,该算法也把序列排列成p×p矩阵,但是只需计算该矩阵每一列所含非零元素的个数即可确定周期为p2的二元序列的k-错线性复杂度,其中同样要求2为模p2的本原元。
对于周期为pn的q元序列(p为奇素数),Xiao等[14]给出计算这类序列在有限域Fq上的线性复杂度。魏仕民等[15]在文献[14]的基础上给出一个确定周期为pn的q元序列的k-错线性复杂度的快速算法。白恩健等[16]在文献[14-15]的基础上进一步给出计算这类序列k-错线性复杂度曲线的一个快速算法。苏明等[17]给出周期为pn的q元序列l–错线性复杂度期望更紧的上界。在这些文献中都要求q为模p2的本原元。然而,在文献[14-16]的算法中都是利用迭代计算的方法得到序列的k-错线性复杂度,计算方式相对复杂,而且随着序列周期的增大,所需迭代的次数相应增加,导致效率较低。为此,本文考虑计算周期为p2的q元序列的k-错线性复杂度的新的快速计算方法,其中p,q为奇素数且q为模p2的本原元。在该方法中,首先把周期为p2的q元序列以行为主序排列为p×p矩阵。与文献[14-15]的迭代算法不同,本文方法只需统计各列中元素出现的次数即可快速确定该序列的k-错线性复杂度。
2 序列的k–错线性复杂的一般结果
设有限域Fq={0,1,2,…,q-1},其中q为素数。ℑ=(tn)n≥0是最小周期为p2的q元序列,不妨把其第一周期元素排列成如下矩阵形式。其中,κ1,κ2,κ3如上所述。



证明由k–错线性复杂度的定义,不妨设εk是Fq上最小周期为p2的q元错误序列且一个周期中仅含有k个非0元素,则序列ℑ在一个周期内改变k个比特后得到新序列记为ℑk,可表示为ℑk=ℑ+εk(modq),即序列ℑ和错误序列εk的对应比特做模q加法运算。用ℑk(X)和εk(X)分别表示新序列ℑk和错误序列εk的生成多项式。为了讨论序列ℑ=(tn)n≥0的k–错线性复杂度,只需讨论gcd(Xp2-1,ℑk(X))的不同情况。由于ℑ(X)=,下面根据序列的复杂度的4种可能取值分别进行讨论。
1)当LC(ℑ)=p2,由定理1知。下面分情况讨论。
② 由引理1的1)知,为使Φ1(X)|ℑk(X),则只需改变序列ℑ中若干项后使新序列ℑk(不妨记为ℑk=对应矩阵排列M(ℑk)每一列的元素之和相等。首先计算M()ℑ中各列元素之和的结果,由于重复出现的次数则为了使改变后的矩阵的各列元素之和相同,只需改变p-κ1列,而每一列只需改变一个元素即可。即当k≥p-κ1,此时可保证Φ1(X)|ℑk(X)。
③由引理1的2)知,为使Xp-1|ℑk(X),则需要通过改变序列ℑ的若干项之后使新序列ℑk(不妨记为)对应矩阵排列M(ℑk)每一列的元素之和为0。由于为M(ℑ)中各列元素之和为0的个数,即M(ℑ)中只有p-κ2列的对应的列元素之和不等于0。注意到,每一列只需要至多改变一个元素的值即可使这一列的各元素之和为0,那么只需改变M(ℑ)中的p-κ2个元素即可使M(ℑK)中的各列元素之和均为0。因此,当k≥p-κ2时,可保证Xp-1|ℑk(X)。
④ 由引理1的3)知,为使Φ2(X)|ℑk(X),则只需改变M(ℑ)每一列中最少的元素,使同一列中各元素(即tj,tj+p,…,tj+(p-1)p)的取值相同,则第j列最少需要改变p-ω(j)项,j=0,1,…,p-1。那么需要改变的最少项数为,即k≥κ3,可保证Φ2(X)|ℑk(X),此时ℑk的最小周期至多为p,则LCk(ℑ)≤p。
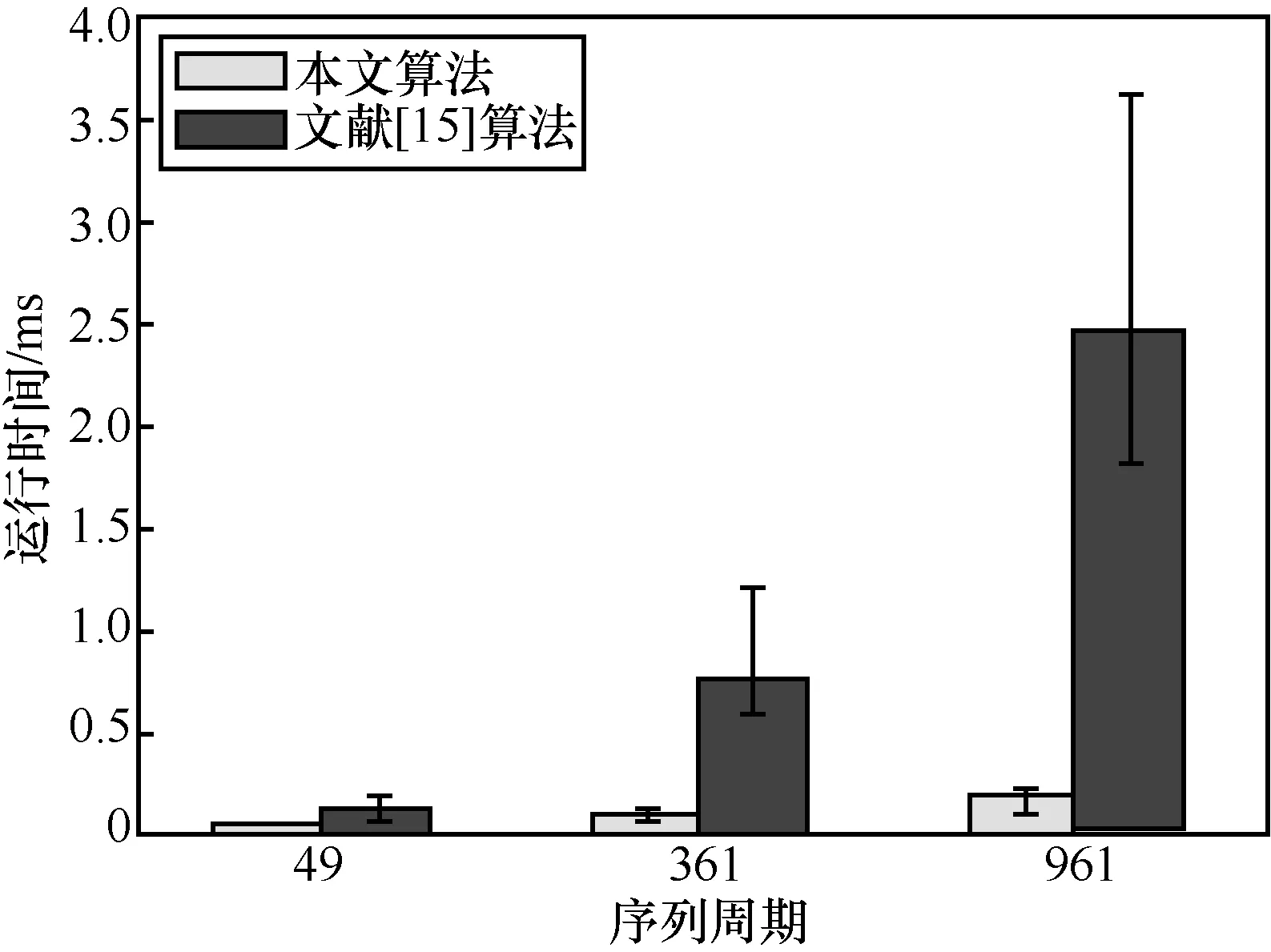
因此,当1≤k 同理讨论可得2)~4)中的结论。 证毕。 设奇素数p,对于任意与p互素的整数u,根据Fermat定理,模p的Fermat商Qp(u)定义为[19] 特别地,当p|u时,定义Qp(u)=0。 由Fermat商Qp(u)的定义容易得到引理2。 引理2[19]对任意的u,v∈,有 1)Qp(uv)≡Qp(u)+Qp(v)(modp) 2)Qp(u+kp)≡Qp(u)-ku-1(modp)其中,k∈Z。 相关文献表明,由Fermat商定义的序列具有良好的伪随机特性[20-22]。杜小妮等[23]利用Fermat商定义了Fq上的q元Fermat序列(fn)n≥0为 其中,q为奇素数,且为了构造平衡序列要求q|(p-1)且。接下来,本文讨论该序列的k–错线性复杂度。 由引理2的2)知,由式(8)定义的q元Fermat商序列的最小周期为p2。 引理3若,则有{Qp(u+kp)(modp)|k=0,1,2,…,p-1}=Zp。 证明设k1,k2∈Zp,若Qp(u+k1p)≡Qp(u+k2p)(modp),由引理2的2)知Qp(u)-k1u-1≡Qp(u)-k2u-1(modp)。又,则k1≡k2(modp)。因为k1,k2∈Zp,所以k1=k2。 证毕。 定理3设p,q为奇素数且q|(p-1),q为模p2的本原元,则由式(8)定义的周期为p2的q元Fermat序列(fn)n≥0的k–错线性复杂为 证明把周期为p2的q元Fermat序列(fn)n≥0按照式(2)的矩阵形式进行排列,即 由引理4和引理1的2)知,(fn)n≥0的线性复杂度为p2-p且κ1=κ2=p。由引理3及式(8)知,。则由定理2的4)即证。 证毕。 例1设p=7,q=3,注意到3为模49的本原元,则由式(8)定义的有限域F3上的三元Fermat序列(fn)n≥0的第一个周期为00212002200100201001011221101001020010022002 12000,把该序列排成如下7阶方阵 注意到,矩阵的各列元素在有限域F3上之和为0,则κ1=7,κ2=7,κ3=24,且LCk(fn)=其结果与定理3完全一致。 设p为奇素数,整数模p2的剩余类集为,g为模p2的本原元,则。记为g模p2的乘法阶,即 定理4设p,q为奇素数且q|(p-1),q为模p2的本原元,则由式(9)定义的周期为p2的q元广义割圆序列(sn)n≥0的k–错线性复杂为 证明首先把周期为p2的q元广义割圆序列(sn)n≥0排列成如式(2)所示的矩阵形式,即 由引理7及式(9)知,对于每个1≤j≤p-1,均有sj=sj+ℓp,其中ℓ=0,1,…,p-1。再由引理6及的定义知,对于1≤j≤p-1中,恰有个sj=i,其中i=0,1,…,q-1。因此,由引理1和定理1知,(sn)n≥0的线性复杂度为p2-1。而对于j=0,由式(9)知s0=0,{sp,s2p,…,s(p-1)p}中也恰有个i,其中i=0,1,2,…,q-1,则 由q为奇素数且q|p-1知 证毕。 例2设p=7,q=3,注意到3为模49的本原元,则由式(9)定义的周期为49的三元序列(sn)n≥0的第一周期为00211200021120202 11201021120 102112020211200021120,同样把该序列排成如下7阶方阵 由上述矩阵知κ1=3,κ2=3,κ3=4且,其结果与定理4完全一致。 首先,本文利用式(8)产生3个周期分别为p2=49、361、961的三元Fermat商序列。然后通过编写Visual C++程序实现本文算法与文献[15]中的算法。对上述3个不同周期的三元Fermat商序列分别运行2个程序求出所有可能的k值对应的k-错线性复杂度,并得到相应的运行时间。此外,从运行结果上看,2个算法的运行结果完全一致。 运行程序的计算机配置:计算机型号为HP ProBook 440G2,Windows 7 64位操作系统,4 GB内存,Intel(R)Core(TM)i5-4210U CPU@1.70GHz 2.40 GHz处理器。由于每次运行所得到的运行时间略有不同,因此本文对上述3个不同周期的序列实例分别连续运行2个程序50次,得到相应的运行时间并取平均值,具体数值如表1所示。 表1 2个算法的平均运行时间 实验数据如图1所示。其中,横坐标表示算法输入的实例序列对应的最小正周期,纵坐标表示运行时间,竖线显示实验数据的最大值、最小值和均值。 图1 2个算法的效率比较 从图1可知,在求周期为p2的q元序列的k–错线性复杂度中,本文算法比文献[15]算法具有明显的优势,随着输入实例序列周期的增大,2个算法的效率之差也增大,而且本文算法的运行时间随输入序列周期的增大变化较小,相对平稳。 本文给出了一个计算周期为p2的q元序列的k-错线性复杂度的新算法,其中p,q为奇素数,且q为模p2的本原元。通过把序列排列成p×p矩阵,然后根据矩阵各列中元素的分布特点即可得到相关结论,而不需要使用文献[14-15]等算法进行迭代计算。由于文献[14]只是用于求q元序列的线性复杂度而非用于求k-错线性复杂度,本文把3个周期为素数平方的三元Fermat商序列作为输入实例分别运行本文算法和文献[15]的算法,求得所有可能的k值对应的k-错线性复杂度及所花费的运行时间,结果表明2个算法的运行结果完全一致,并且本文算法的效率明显更高。另外,从本文的分析过程可知,在设计周期为p2的q元序列时,应注意该序列在排列成p×p矩阵时各列元素的分布情况,进而构造出稳定性好的伪随机序列。3 2类特殊q元序列的k–错线性复杂度
3.1 周期为p2的q元Fermat商序列
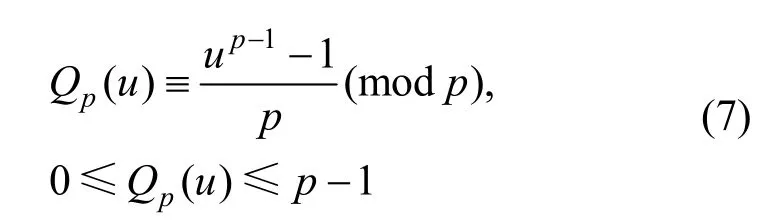
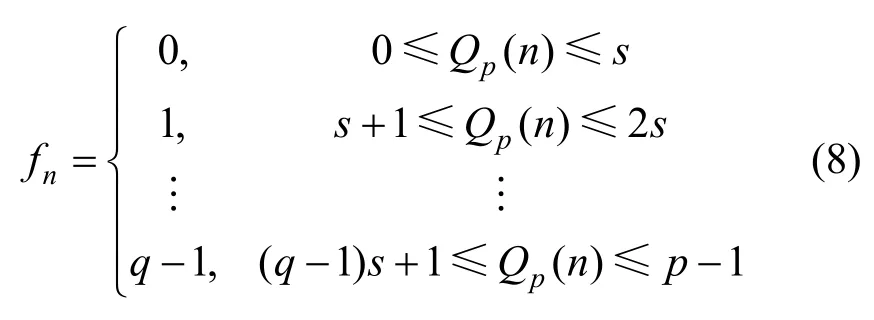

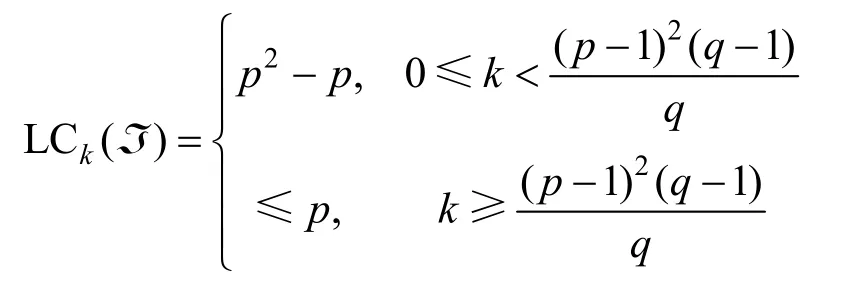
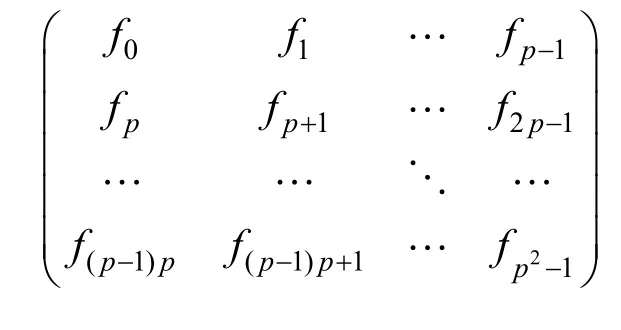

3.2 周期为p2的q元广义割圆序列


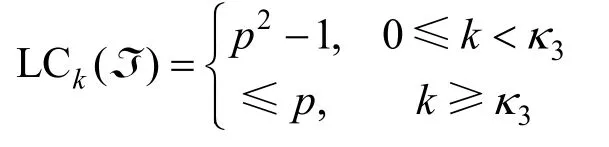
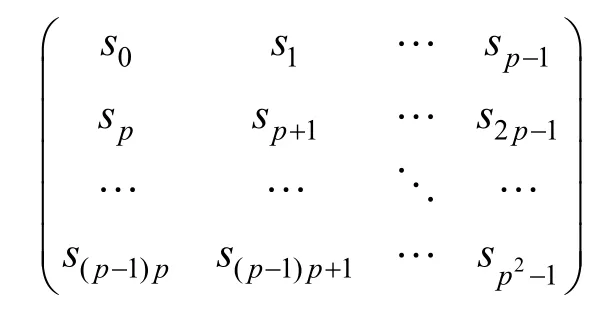
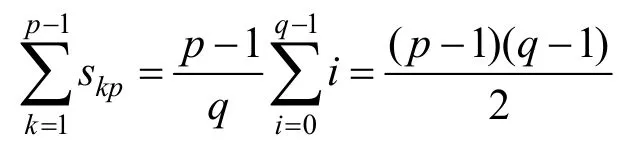


4 效率比较

5 结束语
