从单向优选到双向优选：OT句法与OT语义的新发展❋

邹颖娟

余小强

湖南大学

【提 要】早期的OT句法与OT语义采用单向优选模型，无法较好地解释语言现象中的形式－意义不对称性。由于这两种模型最终都要涉及形式与意义之间的关系，因此在它们的优选过程中存在双向性特征。把双向性特征引入OT，OT模型也由单向优选发展成双向优选。在处理上述语言现象上，虽然双向模型明显优于单向模型，但是仍有一些形－义不对称的语言现象无法得到解释，这些语言现象为OT句法与OT语义的进一步发展与完善提出了新课题。

1.引言

优选理论（Optimality Theory，简称OT）作为生成音系学的模型，最早由Prince&Smolensky（1993，2004）提出。近年来，这套理论已成功地运用到句法领域，目前在语义学领域和语用学领域都颇受关注。优选论的产生源于一个古老的概念，即从一层语言表征（linguistic representation）到另一层的映射（mapping）应由规则（rule）和过滤器（filter）来描写。OT的新贡献在于阐述过滤器（也称为制约条件）是分级并可违反的。因此，违反某些制约条件的成分序列是合法的，只要所有其它的成分序列违反更高一级的制约条件。

OT模型由三个形式部分组成：生成装置（GENerator），评估装置（EVALuator）和层级制约条件系统。这个模型的工作假设是：底层规则和制约条件都是普遍的，语言之间的差异仅存在于制约条件的排列层级。其假设一方面描述语言类型，另一方面又突出语言共性。OT模型具有如下特征：（1）必须有一个输入项集合，对每一个输入项，GEN都会生成一个可能输出项的候选项集；（2）从候选项集中，EVAL为输入项挑选出最优输出项；（3）制约条件集内的制约条件具有普遍性，然而在排列层级上，各语言具有各自的特殊性。就制约条件而言，违反的级别重于违反的次数（Prince&Smolensky 1993，2004；Kager 1999）。也就是说，与违反较低层级制约条件多次的候选项相比，违反较高层级制约条件一次的候选项将失去竞争资格。只有最简约的候选项才是合法的语言学对象，不简约的竞争者都被阻拦。分级制约条件的作用是对候选项进行分级排列，从而使优选成为可能。

OT句法与OT语义研究的是：（1）给定某个语义输入，它的最优表达／形式是什么（OT句法）？（2）给定某个句法输入，它的最优理解／意义是什么（OT语义）？由于形式／意义是一个问题的两个方面，因此，这两个问题的实质就是：什么是最优的形式／意义关系？这种关系是单向的还是双向的？对这个问题的不同回答将引发两类不同的优选模型：单向优选模型与双向优选模型1。下面用对六种不同的语言现象的解释来评介这两类模型，并指出这些模型在分析这些语言现象时的优势与不足。这六种语言现象分别是：歧义（Ambiguity）、变体（Variation 或 Optionality）、无形（Ineffability）、无义（Uninterpretability）、全阻（Total Blocking）和片阻（Partial Blocking）2。

2.单向优选句法与单向优选语义

单向优选句法与单向优选语义主要有三种形式，Beaver&Lee（2004）将其分别称为单纯优选造句（Naive OT Production）、单纯优选解读（Naive OT Comprehension）及单纯交互优选（Naive back-andforth OT）3。它们在解释以上六种语言现象上既有可行的方面，又有严重不足。优选造句采用的是发话人角度，给定某个合法的（well-formed）语义输入，发话者要从句法表达候选集中为这个输入项选择一个最优的句法表达（Bresnan 2000;Aisson 1999;Nefdt 2016）。优选解读采用的是受话人角度，给定某个合法的（well-formed）句法输入，受话者要从语义表达候选集中为这个输入项选择一个最优的语义表达（Hendriks&de Hoop 2001;Helen de Hoop,et al.2004;Samek-Lodovici 2007）。

2.1 单纯优选造句

由于单纯优选造句的输入项是某一既定的意义，因此在单次操作中不可能出现歧义现象。这种现象是多次操作的结果：输入项不同而优选项一致。以OT为例，其意义既可以是「Optimality Theory」，又可以是「Overtime」4。在第一次操作中输入项为「Optimality Theory」，经过GEN及制约条件的评估，得出最优输出项OT。第二次操作的输入项为「Overtime」，得出的最优输出项也是OT。因此，两个OT分属于两个不同的候选项集，由于优选项偶合而形式相同。单纯优选造句就是用这种方法解决了歧义现象。变体则要求在一次操作中，给定某一意义，得出多个最优输出项。由于这种假设有悖于单向优选模式所强调的输入与输出的一一对应性，因此不能解释变体现象。正是这种一一对应性的要求，使其它四种现象也不能在其理论框架内得到解释。

2.2 单纯优选解读

单纯优选解读的输入项是某一既定的形式，因此在一次操作中不可能出现变体现象。与单纯优选造句模型一样，这种现象也是多次操作的结果：输入项不同而优选项一致。如英语联接词that的省略，造成句子的形式不同而意义一致。因此，单纯优选解读可以解释变体现象。以形式1）I think that Mary is clever与形式2）I think Mary is clever（无连接词that）为例：第一次操作输入项为形式f1，产生优选项意义m1「我认为玛丽聪明」，第二次操作输入项为形式f2，产生优选项意义m2「我认为玛丽聪明」。这两个优选项是两个不同候选项集中的优选项，在这种条件下，m1可以等同于m2。由于其它五种语言现象都违背了一一对应性的要求，因此不能在此框架内得到解释。

2.3 单纯交互优选

与上述两类单纯优选模型一样，单纯交互优选模型也不涉及形式与意义之间的配对集，只是前两类模型的简单合并。尽管在造句和解读中制约条件相同，这种模型并没有指派给形式／意义之间以一致的联系（Antilla&Fong 2001）。以歧义为例：输入项为意义「Optimality Theory」，先使用单纯优选造句得到形式OT，再使用单纯优选解读，得到的可能并不是原始义「Optimality Theory」，而可能是某一个新的意义「Overtime」。变体也可能出现类似情况。例如，输入项为形式f1I think that Mary is clever，运用单纯优选解读，得到意义m1「我认为玛丽聪明」，以此意义为输入项，再运用单纯优选造句，得到的形式有可能是不同于f1的f2I think Mary is clever（无连接词 that）。其它四类现象由于在上述两类单纯优选模型中都不能得到解释，因此对两类模型只做了简单合并处理的单纯交互优选模型自然也无法解释这四类现象。

为了弥补单向优选模式的不足，语言学家们提出了双向优选模式。这是因为，从本质上说，单纯优选造句是一条既与句法相关又与语义相关的理论，单纯优选解读也是如此。这两种单向理论最终都要涉及形式与意义之间的关系，具有双向性特征。

3.双向优选句法与双向优选语义

优选论中的双向优化有其深厚的理论渊源5，句法中的双向概念与语义中的双向概念是互补的。如果只从发话者的角度出发，就无法解释受话者的理解取向（Preference）；若只从理解的角度出发，则无法解释阻碍效应。单纯优选造句通常忽略了句法歧义现象，而这种现象恰恰表明优化的双向性。在这种框架下，GEN可以用同一个解读与多个不同的形式匹配。可选形式的存在可能造成阻碍效应，对可能的优选解读项产生重大影响。因此，无论是在理论性还是在实证性方面，双向优选强于单向优选。

在双向OT中，通常假设有一个形式集F，一个意义集M，发话人与受话人合作确立双方都认可的形式／意义对（Blutner 2001;Helen de Hoop&Malchukov 2007;Brattico 2014;Klecha 2018）。Jäger（2002）详细讨论了最优形式／意义对的触发机制。根据对相关形式违反制约条件层级的计算，发话人为某一给定的意义m0选择优选项形式f0，即候选项集内违反最低层级制约条件的候选项。然后，受话人根据他对相关意义违反制约条件层级的计算，为形式f0选择他认为是最优的优选项意义m1。随后，又根据自己的形式取向，为m1选择形式f1，从而形成螺旋型模式。如果发话人与受话人最终都选择了相同的形式和意义，那么，形式／意义的最优对就形成了。如果［f，m］是这种技术性概念下的最优对，那么，选择f是表达m的最优方式，发话人与受话人两者的取向都得到了匹配。

下文将介绍双向优选中影响最大的四种模型：强式双向优选（Strong Bidirectional OT），弱式双向优选（Weak Bidirectional OT），解读优先（IP Asymmetric OT）及造句优先（PI Asymmetric OT）6。

3.1 强式双向优选

强式双向优选是由Blutner（2001）首先提出的一种双向模型。其主要观点为，为使表达合法，一个形式／意义对[f,m]在双向优选中都必须是优选项7。

形式／意义对[f,m]是强式优选项，当且仅当

（1）[f,m]GEN，

（2）无其它对[f',m]GEN，且[f',m]＞ [f,m]，

（3）无其它对[f,m']GEN，且[f,m']＞ [f,m]。

强式优选剔除仅在一个方向上的形式／意义优选对。它的优点在于，若制约条件的排列层级相同，强式优选在优选项的数量上少于单纯优选造句或单纯优选解读所产生的优选项，从而能够解释无形及无义现象。无形现象可以这样解释：第一，在造句模型中，给定某意义m，得到优选项f；第二，在解读模型中，输入项f所产生的优选项m'不同于造句模型中的意义m。因此，意义m'阻断了意义m，使得m有义而无形。无义现象也可以通过类似的步骤得到解答。强式优选还为全阻提供解答。例如有语义相同的两种形式f1cheaper与f2more cheap，优选项都为m1「cheaper」。在解读模型中，两种形式不属于同一个候选项集因而都合乎语法。在强式优选模型中，形式f2被更简约的形式f1阻断，形式／意义对[f2，m1]被排除在优选项之外。

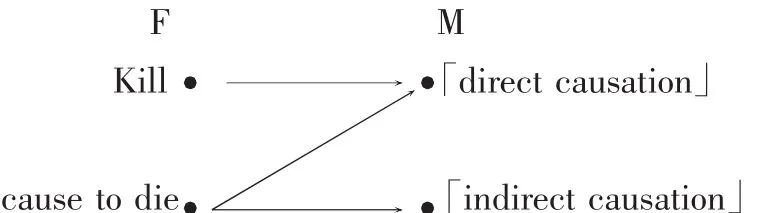
虽然强式优选模型为无形、无义及全阻等现象提供一个统一的解释，然而对歧义及变体现象，强式优选无法解答。这个模型的另一个不足之处在于阻断效应过于严格。例如，根据模型，形式f1kill阻断了形式f2cause to die，因此，f2应该无义。这种推论与事实相悖。实际上，f1对f2的阻断只是部分的，非完全的，这一点笔者在3.2节中再详细说明。

3.2 弱式双向优选

弱式双向优选是强式优选模型的变体，其目的是解释片阻现象。在弱式优选模型中，强式优选的失败者可进入后一轮或后几轮的竞争。依此类推，可以发现，在弱式优选中，每个候选项都能成为优选项。

形式／意义对[f,m]是弱式优选项，当且仅当

（1）[f,m]GEN，

（2）无其它弱式优选对[f',m]GEN，且[f',m]＞ [f,m]，

（3）无其它弱式优选对[f,m']GEN，且[f,m']＞ [f,m]。

弱式优选的使用通常被看作是形式与意义之间不断删除连结（Pruning）与增加连结（grafting）的过程。以形式kill与cause to die为例，其可能的解读有「direct causation」和「indirect causation」。弱式优选的过程分为三个阶段：单纯解读与造句；删除连结；增加连结8。

阶段1 单纯解读与造句

阶段2删除连结

阶段3 增加连结

Blutner（2001）认为，弱式优选抓住了语用推理的本质，即无标记形式趋于在无标记语境下使用，有标记形式趋于在有标记语境下使用（Levinson 2000）。这无疑是弱式优选的优势所在。然而，与其优势相比，弱式优选的问题更为突出。对已有的优选对[f1，m1]，它既不能增加一个新的意义 m2，使得[f1，m2]成为优选对；也不能增加一个新的形式f2，使得[f2，m1]成为优选对。增加连结的技术可能使无形的概念成为有义有形，或者使无义的表达变得有形有义。这些都是弱式优选解释力不足的表现。弱式优选模型更为严重的不足在于它过强的生成力（over-generation）。由于每一个候选项都可能成为不同阶段的优选项，因此，大量的不合语法的候选项都会被纳入到优选项范畴，从而造成生成力过强9。

3.3 解读优先

解读优先是Wilson（2001）首先提出来的双向优选模型。根据Wilson，解读优先就是在优选过程中，解读先于造句，解读优化的结果影响造句优化的候选项集。这种模型与造句优先模型一样，都具有非对称性（asymmetry）的特点。解读优先的主要观点是：（1）解读。给定任何形式／意义对[f,m]，找到关于形式f的最和谐语义解读；（2）造句。给定输入项意义m，把解读阶段所有的、使[f,m]为优选项的形式f作为候选输出项，再使用传统的OT句法处理受限的候选项集。值得注意的是，造句阶段的形式／意义对集是解读阶段形式／意义对集的子集。也就是说，优选对的意义集在解读阶段与造句阶段是一样的，而就形式集而言，造句阶段少于解读阶段。

这种模型可以用来解释无形，全阻及片阻效应。由于这种模型强调的是解读优先，因此，与单纯解读优选模型一样，它能顺利地解决无形现象。解读优先优于单纯解读的地方在于，前者能够解释全阻与片阻效应，而后者却不行。Wilson所提出的解读优先模型对片阻的解释可用图表表示如下10：

阶段1解读

阶段2造句

2.1

2.2

解读优先=2.1M∪2.2M，即

3.4 造句优先

与解读优先模型相对，Zeevat（2001）提出的造句优先模型保留了传统的单向造句模型，使用造句的结果限制解读的候选项集。造句使用传统的OT句法制约条件集PROD，解读是更为复杂的二阶过程，既包括PROD也包括挑选意义的制约条件集PRAG。解读中的形式／意义对集是造句中形式／意义对集的子集。使用两个不同的制约条件集是Zeevat不同于Wilson及其它双向优选模型的最大之处。Zeevat认为，这种模型能够成功地解决歧义、无形、无义以及全阻现象。

由于造句优先的基础是传统的单向造句模型，因此，歧义现象能够得到完美的解答。Beaver&Lee（2004）对它是否能够解释无形现象提出了质疑。他们认为，从造句的角度看，任何意义输入项都必须给出某个优选形式作为输出项。若无形是指无法言表的意义，那么，造句优先模型不能预测任何无形现象，笔者也赞同这一观点。由于第一阶段的操作与单纯造句一致，对任一意义输入，可能有许多偏离输入意义的形式序列。这些形式序列在造句优先模型里都是无义的。全阻现象可以用形式f1cheaper，形式f2more cheap与意义m1「cheaper」之间的关系来论证。要解读形式f2more cheap，其意义必须是more cheap所表达的意义「cheaper」。然而最优对[f1，m1]表明，意义「cheaper」的最优表达式是形式f1cheaper。由于没有其它意义与形式f2more cheap匹配，形式f2就成为无义，被形式f1成功阻断。

4.结语

本文通过概述七类OT模型对六种语言现象的解释及其在解释中所存在的问题，从中得出两个结论：第一，从解释现象的数量上看，双向模型明显优于单向模型；第二，没有一个模型能够解释全部的六种语言现象。结论一说明了从单向优选发展到双向优选的科学性与正确性；结论二则说明，现今的双向模型在处理形式-意义的不对称性上仍存在不少问题，需要不断改进。笔者希望，双向优选所面临的问题能够在不久的将来得到完美的解决。

注释：

1 单向优选与双向优选的主要差别在于，单向优选考虑的只是单纯的输入项和输出项，而双向优选考虑的是输入项和输出项之间的配对关系。

2 歧义就是我们说的一形多义现象，如OT可理解为「Optimality Theory」或「Overtime」。变体则指一个意义用多个形式来表示，如「我认为玛丽很聪明」这个含义，既可用I think that Mary is clever，也可用I think Mary is clever（无连接词that）来表示。在意大利语中，一个单句内不能同时出现两个疑问词。要表达意义「谁吃了什么」，我们不能用Who ate what，而必须用Who ate something，这就是我们说的无形。无义可以用Chomsky（1957）一个有名的例子来说明：Colorless dreams sleep furiously。全阻是指一种形式与某意义的关系阻断了另一种形式与之的关系。如我们用形式wrote表达意义「wrote」，从而阻断了形式writed与意义「wrote」之间的关系。片阻指的是两种形式与两种意义之间的关系。如形式1 knife与形式2 cutter都与意义1「knife」相关，knife与「knife」的匹配关系阻断了cutter与「knife」的关系。形式2cutter只能与剩下的意义2「non-canonical cutting implemen「t匹配而形成片阻。

3 Beaver&Lee所说的单纯优选造句实际上就是Grimshaw（1997）提出的OT句法，它最接近OT音系学模型。它以某种意义表征作为输入，由函数GEN产生候选输出项集。线性排列的制约条件集将挑选出候选表层形式中的优选项。单纯优选解读也就是Hendricks&de Hoop（2001）所倡导的OT语义，其输入是表层句法形式，GEN产生候选意义项集，线性排列的制约条件集挑选出与表层形式匹配的意义优选项。单纯交互优选也是Hendriks&de Hoop（2001）所讨论的一种优选模型，它不涉及形式与意义之间的配对集，只是前两类模型的简单合并。尽管在造句和解读中制约条件相同，这种模型并没有指派给形式／意义之间以一致的联系。例如，输入项为意义m1，先使用单纯优选造句得到某形式f1，再使用单纯优选解读，我们得到的可能并不是原始义m1。在下文中我们可以看到，由于这些模型都是单向优选，因此具有较大的局限性。

4 本文中的形式用斜体标识，意义用「」标识。

5 双向优化的观点在以下的理论假设中都有或多或少的体现。根据基础丰富性假设（richness of the base），所有语言语法的输入项集都是相同的，在表达方面不受任何限制。因此，在许多情况下，都会出现多个输入单一输出的结构。Prince&Smolensky（1993,2004）,ItÔ,Mester&Padget（t1995）引入了词汇优化（lexicon optimization）的算法来处理这个问题。这种算法计算每一个输入项产生优选项所违反的制约条件的次数，最少违反制约条件的输入-输出对就是优选对。因此，词汇优化是双向的，既从输入到输出，又从输出到输入。人类语言的语句分析（parsing）也是优选论研究的相关领域。在语句的分析过程中，理解也贯穿于过程的始终，分析机制（parser）根据表层输入优化底层结构（Müller 2001）。这些观点表明，优化是一个双向相关的概念。

6 强式双向OT与弱式双向OT是由Blutner（2001）提出的，解读优先OT是Wilson（2001）提出的双向优选模型，而造句优先OT（PI Asymmetric OT）是由Zeeva（t2001）首先提出的。

7 在Blutner（2001）所提出的强式双向优选公式中，符号“＞”表示“较……更和谐”或“较……更简约”。

8 在第一阶段中，所有的单向优选连结都用实线箭头标注了出来。除最优连结外，阶段1中还有两条虚线箭头。这两条虚线连结的是单向次优选项（sub-optimal candidates），是这一阶段竞争的失败者。在阶段2中，两条单向优选连结被阻断，只留下一对双向优选连结。在阶段3中，由于交叉的两条单向优选连结被阻断，次优选项再次参与竞争，成为第二轮竞争中的最优连结。

9 由于篇幅所限，我们不能完整、详细地说明弱式优选模型过强的生成能力，对此感兴趣的读者可参考Lee Hanjung（2001）。

10 由于解读优先模型对全阻效应的解释与强式优选模型一致，因此，我们在3.3节中不再详述。