粘性Cahn-Hilliard方程指数吸引子的存在性

苏小虎，姜金平

(延安大学数学与计算机科学学院，陕西延安716000)

粘性Cahn-Hilliard方程是由Novick cohen等在1958年提出的，用来描述带粘性的二物质相互扩散，许多学者在文献[1,2]对该方程进行了研究，文献[3,4]研究了粘性Cahn-Hilliard方程全局吸引子存在性，文献[5]基于非线性测度证明Cahn-Hilliard方程强解的全局吸引子。受文献[6]启发，参考其方法进一步讨论粘性Cahn-Hilliard方程的指数吸引子的存在性问题。

考虑如下粘性Cahn-Hilliard方程指数吸引子的存在性：

(1)

其中Ω⊂Rn(n≤3)是具有光滑边界的有界区域。

1 预备知识

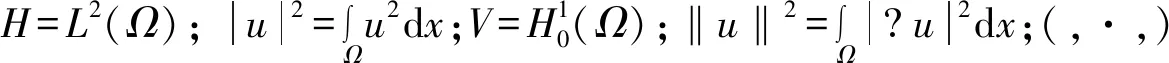
定义1.1[6]设X是一个度量空间，半群S(t):

X→X,集合M⊂X,如果满足：

(1)(紧性)紧集M⊂X,并有有限分形维数；

(2)(不变性)集合M是正不变集，即

S(t)M⊂X;

(3)(吸收集)集合M是一个指数吸收集，即存在一个常数l>0,使得对任意有界子集B⊂X,存在一个常数k=k(B)>0，使得：

dist(S(t)B,M)≤ke-lt。

则M称是半群S(t)的指数吸引子。

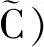
∀x∈B,t≥T。

其中：这里的Pm:X→X1是有界投影算子；m是X1的维数；则实函数k(m)满足：

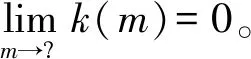
定理1.1[6]设X是一个Banach空间，S(t)是空间X上的半群，如果满足下列条件：

(1)(有界吸收集)S(t)存在一个有界吸收集B⊂X；

则S(t)存在指数吸引子。

2 指数吸引子的存在性

设f是Lipschitz连续函数，并且满足下列条件

(2)

(3)

其中：λ1是-Δ在V中的第一个特征值。

从(2) 可得，存在常数C0和C1,使得：

f(s)s≤(λ1-C0)s2+C1,s∈R。

(4)

引理2.1[6]设f满足上面的条件(2)和(3)，u0∈V,则对于我们的方程(1)对应的解半群S(t)在空间V中有有界吸收集，即对V中任意的有界集B，存在t1(B)>0,ρ1>0,使得∀u∈B有：

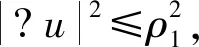
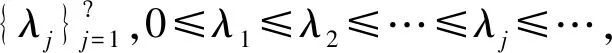
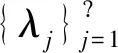
令Hm=Span{e1,e2…,em}⊂H,Pm:H→Hm是一个正交投影算子。对于任意u∈H,我们有

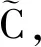
引理2.2 设函数f满足(2)和(3)，u0∈V,则对于我们的Cahn-Hilliard方程(1)对应的解半群S(t)在空间H中有有界吸收集，则对H中任意的有界集B,存在t1(B)>0,ρ1>0,使得∀u∈B有：

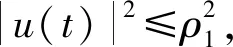
证明取u作为实验函数作用于(1)式，我们有：

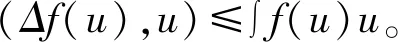
由(4)式，我们可以得到：

(λ1-C0)|u|2+C1|Ω|，

C|u|2+C1|Ω|，

因此，有：

2C|u|2+2C1|Ω|。

我们知道：

其中：这里的λ1是-Δ在V中的第一个特征值。

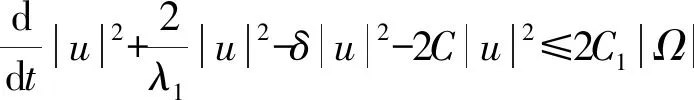
因此，有：

利用Gronwall引理，我们得到：

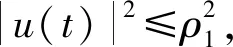
引理2.3 设f满足(2)式和(3)式，那么半群

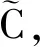
∀u0∈B。

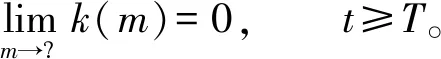
证明取-Δu2与(1)式作内积，我们有：

(Δf(u),-Δu2)≤|f(u)||Δu2|。

(5)

因为

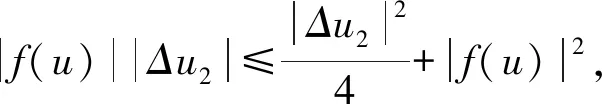
由(5)式可知：

利用(4)式，可得：

(λ1-C0)|u|2+C1|Ω|。

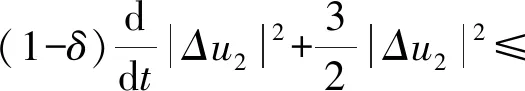
2(λ1-C0)|u|2+2C1|Ω|。

由引理2.2及Poincare不等式，我们可以得到：

利用Gronwall引理，我们有：

当m→时，λm→+。

由引理2.2和2.3的证明，我们可得出如下主要结论：

定理2.1 设Ω⊂Rn(n≤3)是具有光滑边界的有界区域，f满足(2)式和(3)式，则方程(1)存在半群S(t)且在V上存在指数吸引子。