双参数n阶α次积分C半群

赵丹丹，赵华新

(延安大学数学与计算机科学学院,陕西延安716000)

Banach空间中的线性算子半群理论是解决实际问题的重要工具，在泛函分析理论的各方面有着重要应用，许多学者对其做了进一步的研究[1,2]。刘曼、郭玲利[3]引入n次积分C半群的概念并研究其性质推导出一个表示定理；徐敏等[4]、黄翠[5]研究了双参数C半群及其生成元与单参数C半群生成元的关系；张明翠、宋晓秋等人[6,7]在2014年给出单参数n阶α次积分C半群的概念并讨论其相关问题。本文在以上文献研究的基础上，将单参数n阶α次积分C半群推广到双参数n阶α次积分C半群，得到双参数n阶α次积分C半群的定义，并对其性质进行研究。

1 预备知识

在本文中，X为无限维的复Banach空间，B(X)是X上有界线性算子全体所成的Banach代数；D(A)为线性算子A的定义域，在全文中规定所有n∈N，α≥0。

JnT(t)表示T∈C([0,+),X)的n次积分，即

T=0当且仅当存在n>0使JnT(t)=0,t≥0。

2 双参数n阶α次积分C半群的定义

定义1 设n∈N，α≥0，C∈B(X)是单射,{T(t,s)}s,t≥0⊂B(X)强连续，若存在算子A=(A1，A2)使(1)(2)(3)式成立，

(1)∀x∈X,t,s≥0,JnT(t,s)∈D(A)，

(2)CT(t,s)=T(0,s)T(t,0) ；

(3)∀x∈D(A),t,s≥0,JnT(t,s)∈D(A) ,

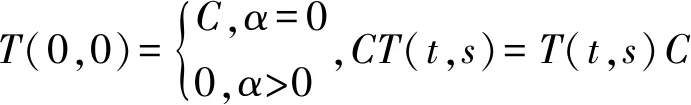
当α=0时，{T(t,s)}s,t≥0是双参数n阶C半群。

3 主要结论

定理1 设A=(A1，A2)是双参数n阶α次积分C半群{T(t,s)}s,t≥0的次生成元，则对任意x∈

D(A),有T(u,v)x∈D(A)且

AT(u,v)x=T(u,v)Ax,∀u,v≥0。

证明由于{T(t,s)}s,t≥0强连续，故有：

JnT(t,s)AT(u,v)x=

T(u,v)JnT(t,s)y=JnT(u,v)T(t,s)y=

JnT(t,s)T(u,v)y=JnT(t,s)T(u,v)Ax。

又由y∈X的唯一性，有T(u,v)y∈X且唯一，则有T(u,v)x∈D(A)，且

AT(u,v)x=T(u,v)Ax,∀u,υ>0。

综上所述，定理得证。

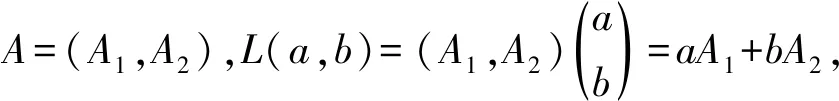
(1)∀x∈X,t≥0,JnT(t,0)∈D(A1)，

(2)∀x∈X,s≥0,JnT(0,s)∈D(A2)，

证明由双参数n阶α次积分C半群满足线性变换，

则有∀x∈X,t,s≥0,JnT(t,s)∈D(A)，

A1JnT(t,0)x+A2JnT(0,s)x。

则取s=0时有：

A1JnT(t,0)x+A2JnT(0,0)x。

又由双参数n阶α次积分C半群的定义

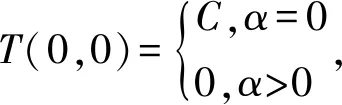
可知A2JnT(0,0)=0。故有

∀x∈X,t≥0,JnT(t,0)∈D(A1)。

同理可证当t=0时有：

∀x∈X,s≥0,JnT(0,s)∈D(A2)。

综上所述，定理得证。

定义2[6]算子族{T(t)}t≥0⊆B(X)称为指数有界的，如果存在M≥0，ω∈R使‖T(t)‖≤Meωt,∀t≥0成立。

定理3 设{T(t,s)}s,t≥0是双参数n阶α次积分C半群，则存在M≥0，ω≥0使得

‖T(t,s)‖≤‖C-1‖Meω(t+s)。

证明由定义2单参数n阶α次积分C半群的指数有界性可得：

∃M1≥1，ω1≥0,使得‖T(t,0)‖≤M1eω1t。

同理∃M2≥1，ω2≥0,使得

‖T(0,s)‖≤M2eω2s。

又由双参数n阶α次积分C半群的定义中的(2)式CT(t,s)=T(0,s)T(t,0)可得

‖CT(s,t)‖=‖T(t,0)T(0,s)‖，

‖T(t,s)‖=‖C-1T(t,0)T(0,s)‖≤

‖C-1‖‖T(t,0)T(0,s)‖≤

‖C-1‖‖T(t,0)‖·‖T(0,s)‖≤

‖C-1‖M1eω1t·M2eω2s。

令ω=max{ω1,ω2}≥0且M=M1·M2≥0，

有‖T(t,s)‖≤‖C-1‖Meω(t+s)。

综上所述，定理得证。