中考青睐的“方程与不等式”题型

程玉娟

方程与不等式是数学中最基本、最核心的知识之一，是解决数学问题的有力工具，同时又是解决实际问题的桥梁。各地中考既有对基础知识、基本技能的考查，如直接解方程、方程组等，又有对同学们综合运用知识的能力的考查，如方案规划问题、函数问题等。下面，我们对方程与不等式的常考题型进行归纳研究。

一、直接解方程（组）或不等式（组）

例1（2018·黑龙江齐齐哈尔）解方程：2（x-3）=3x（x-3）。

【解析】移项后，提取公因式x-3，利用因式分解法求得一元二次方程的解即可。

解：2（x-3）=3x（x-3），

移项得：2（x-3）-3x（x-3）=0，

整理得：（x-3）（2-3x）=0，

x-3=0或2-3x=0，

解得：x1=3或x2=。

【点评】一元二次方程的解法有直接开平方法、配方法、公式法和因式分解法。本题是利用整体思想、提取公因式法求解。

例2（2018·江苏无锡）方程组的解是_______。

【解析】利用加减消元法求解可得。

解：

②-①，得：3y=3，

解得：y=1，

将y=1代入①，得：x-1=2，

解得：x=3，

【点评】解二元一次方程组的思想方法是消元，将二元变成一元，再去解一元一次方程即可。消元的方法有两种：一是加减消元，另一种是代入消元。同学们要根据实际情况选择合适的方法。

二、方程与不等式的互化

【解析】解出不等式组的解集，与已知解集-1＜x＜1比较，可以求出a、b的值，然后相加，求出（a+b）的2009次方，可得最终答案。

解：由不等式得x＞a+2，x＜b，

∵-1＜x＜1，

∴a=-3，b=2，

∴（a+b）2009=（-1）2009=-1。

故答案为-1。

【点评】本题是已知不等式组的解集，求不等式中另一个未知数的问题。可以先将另一个未知数当作已知处理，求出解集并与已知解集比较，构造方程，进而求得另一个未知数。

三、在方案规划问题中的应用

例4（2018·湖北咸宁）为拓宽学生视野，引导学生主动适应社会，促进书本知识和生活经验的深度融合，我市某中学决定组织部分班级去赤壁开展研学旅行活动。在参加此次活动的师生中，若每位老师带17个学生，还剩12个学生没人带；若每位老师带18个学生，就有一位老师少带4个学生。现有甲、乙两种大客车，它们的载客量和租金如表所示。

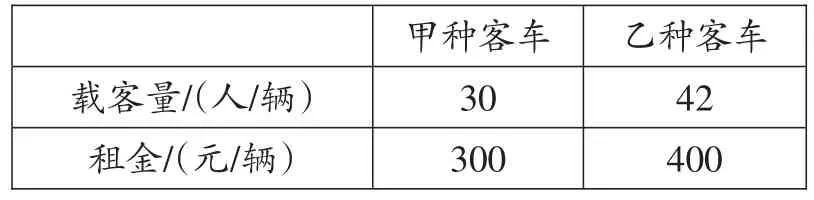
___载客量/（人__________/辆）____租金/（_____________元/辆）________________________________________________甲种客车30_________300________乙种客车_42____400____

学校计划此次研学旅行活动的租车总费用不超过3100元，为了安全，每辆客车上至少要有2名老师。

（1）参加此次研学旅行活动的老师和学生各有多少人？

（2）既要保证所有师生都有车坐，又要保证每辆客车上至少有2名老师，可知租用客车总数为________辆。

（3）你能得出哪几种不同的租车方案？其中哪种租车方案最省钱？请说明理由。

【解析】（1）设老师有x名，学生有y名，得出二元一次方程组，解出即可。

（2）根据老师人数和师生总人数，再由已知条件，即可求出客车总数为8辆。

（3）设租用x辆乙种客车，则甲种客车数为（8-x）辆，由题意得出 400x+300（8-x）≤3100，得出x取值范围，再分析即可。

解：（1）设老师有x名，学生有y名。

答：老师有16名，学生有284名。

（2）∵每辆客车上至少要有2名老师，

∴16÷2=8，即汽车总数不能大于8辆。

又∵16+284=300，即要保证300名师生有车坐，所以汽车总数不能小于（取整为8）辆，

综上，可知汽车总数为8辆。

故答案为：8。

（3）设租用x辆乙种客车，则甲种客车数为（8-x）辆。

∵车总费用不超过3100元，

∴400x+300（8-x）≤3100，

解得：x≤7。

为使300名师生都有座，

∴42x+30（8-x）≥300，

解得：x≥5，

∴5≤x≤7（x为整数），

∴共有3种租车方案：

方案一：租用甲种客车3辆，乙种客车5辆，租车费用为2900元。

方案二：租用甲种客车2辆，乙种客车6辆，租车费用为3000元。

方案三：租用甲种客车1辆，乙种客车7辆，租车费用为3100元。

故最节省费用的租车方案是：租用甲种客车3辆，乙种客车5辆。

【点评】本题第一问根据学生数与老师数之间的等量关系列方程组，从而得解，运用的是方程模型。第三问根据费用的不等关系以及在保证每人都有座位的前提下，列出不等式，得出x范围，再根据实际情况，x要取整数，从而在范围内取有限的整数解，得出结果。此种题型是方程（组）与不等式（组）非常具有代表性的应用，不论是从年份来看，还是从各个地区来看，在中考中最受青睐。此题分值比较大，难度中等偏上。

四、在函数中的应用

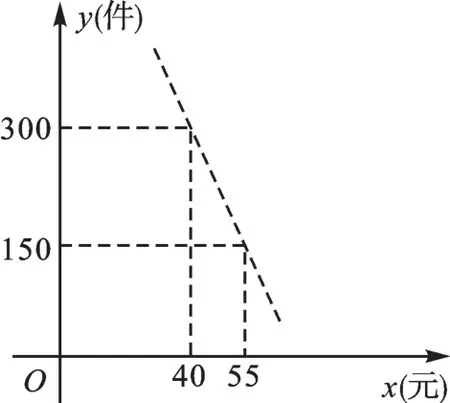
例5（2018·江苏扬州）“扬州漆器”名扬天下，某网店专门销售某种品牌的漆器笔筒，成本为30元/件，每天销售y（件）与销售单价x（元）之间存在一次函数关系，如图所示。

（1）求y与x之间的函数关系式。

（2）如果规定每天漆器笔筒的销售量不低于240件，当销售单价为多少元时，每天获取的利润最大？最大利润是多少？

（3）该网店店主热心公益事业，决定从每天的销售利润中捐出150元给希望工程。为了保证捐款后每天剩余利润不低于3600元，试确定该漆器笔筒销售单价的范围。

【分析】（1）可用待定系数法来确定y与x之间的函数关系式。

（2）根据利润=销售量×单件的利润，然后将（1）中的函数关系式代入其中，求出利润和销售单价之间的关系式，然后根据其性质来判断出最大利润。

（3）首先得出w与x的函数关系式，进而利用所获利润等于3600元时，对应x的值，根据增减性，求出x的取值范围。

【解答】（1）设y=kx+b，

故y与x之间的函数关系式为：y=-10x+700。

（2）由题意，得-10x+700≥240，

解得x≤46，

设利润为w，w=（x-30）·y=（x-30）（-10x+700）=-10x2+1000x-21000=-10（x-50）2+4000，

∵-10＜0，

∴x＜50时，w随x的增大而增大，

∴x=46时，w大=-10（46-50）2+4000=3840。

答：当销售单价为46元时，每天获取的利润最大，最大利润是3840元。

（3）令w-150=-10x2+1000x-21000-150=3600，

即-10（x-50）2=-250，

x-50=±5，

解得x1=55，x2=45，

当45≤x≤55时，捐款后每天剩余利润不低于3600元。

【点评】利用方程或方程组求二次函数解析式基本上属于必考题。二次函数的表达式有3种：一般式、顶点式和交点式。根据所给条件选择恰当的表达式，建立方程模型即可求解。