几类“漏解”情形的应对策略

王苏文

(浙江省诸暨市浬浦中学 311800)

要想解决漏解问题必须分清漏解的原因所在，根据平时解题出现漏解的原因可从以下几个方面去分析.

一、公式适用范围有否疏忽

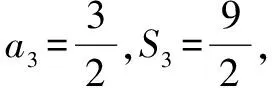
剖析等比数列的前n项和包括q=1与q≠1两个公式，因此，在没有确定公比是否为1时需对q进行分类讨论求解或者避免讨论，直接用常规的方法去求.

剖析双曲线的渐近线方程是由不同的焦点所在位置确定其方程形式，因此，在没有确定位置时需进行分类讨论求解.

应对策略在平时应用公式时务必清楚所需条件，防止适用范围不注意而导致漏解.

二、概念有否模糊不清

例3 设函数y=logax(a>0,a≠1)在区间[2,4]上的最大值比最小值大2，求实数a的值.

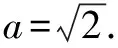
剖析由于对数函数的单调性虽一致，但还有可能递增或递减，故需对底数a进行讨论，而上述解答盲目地将其看成增函数，导致出现“漏解”.

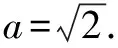
应对策略在平时解题时对概念问题务必清楚，防止在概念中的疏忽而导致漏解.

三、隐含条件有否遗忘

例4 设x≥0,y≥0，且x+2y=1，求z=x+3y2的最值.

误解由条件x+2y=1可得x=1-2y，代入z=x+3y2中得：

剖析由于题目解题中缺少对隐含的发掘，故而导致结论的错误.

应对策略在解题中要充分挖掘题目中所给条件，防止表面现象而忽视隐含的条件产生而导致漏解.

四、思维有否定势惯性

例5 函数y=lg|ax-1|的图象对称轴为直线x=2，求实数a的值.

正解由于图象关于直线x=2对称，设图象上任意一点(x,y)，关于x=2对称的点为(4-x,y)也在图象上，故|ax-1|=|a(4-x)-1|.

整理得2a(x+2)=0或2a-1=0.

由于对于定义域下的任意x都要成立，

例6 设直线l1:y=x+4，直线l2:y=kx+1，与两坐标轴围成的四边形有外接圆，求实数k的值.

误解根据题意，与坐标轴围成的四边形有外接圆(即四边形的对角互补).结合图形，显然当直线l1与l2垂直.根据斜率乘积为-1，马上得到k=-1.

剖析此题是根据四边形有外接圆的结论要求是对角互补.但事实上我们考虑问题还是显得有点不全面，只抓住它包含了直角坐标系下的直角，而忽略了假如不包含这个直角是否有可能成立呢？

正解若包含了直角坐标系下的直角，那么结合图形(一)，显然当直线l1与l2垂直时，四点共圆.根据斜率乘积为-1，可得k=-1；若不包含直角坐标系下的直角，结合图形(二)，由于∠DAB=45°，要存在这样的直线只要∠BCD=135°即可.

故直线AD与直线BC只要平行，就可以得到四边形ABCD有外接圆.

根据题意,可得k=1.

综上可知：满足条件的实数k为-1或1.

应对策略在平时解题中由于对问题的思维惯性，导致在思考问题时不够全面而漏解.

通过上面五个例题的分析可以发现我们在平时的解题中，有很多隐患存在，极易使我们在计算过程中出现“漏解”的问题.因此我们在学习过程中时不要对结论的模糊记忆，对概念不可模棱两可，考虑问题不要丢三落四，这样才可以使我们在解题中少出现“漏解”问题，甚至不出现.