横波干涉中振动加强点、振动减弱点判断方法的系统总结
2019-03-27黄涛蔡意安坤
黄 涛 蔡 意 安 坤
(河南省息县第一高级中学 464300)
频率相同、相位差恒定的两列波相遇时会发生干涉,在叠加区域中,一些质点的振动幅度始终是最大,这些质点被称为振动加强点,叠加区域中所有的振动加强点组成振动加强区;一些质点的振动幅度始终是最小,称为振动减弱点,所有振动减弱点构成振动减弱区.那么如何判断振动的质点是振动加强点和减弱点呢?在高中阶段,按使用的手段划分,有观察和计算两类方法,我们来详细讨论.
一、观察法
“观察法”是指观察某一时刻两列干涉波的干涉图样,根据波峰或波峰叠加情况,来判断叠加区域质点振动情况.“观察法”也分为“叠加法”和“连线法”.
1.叠加法
两列频率相同、相位差恒定的波相遇,发生干涉.由波的叠加原理可知,波峰与波峰相遇处始终是振动加强点,波峰与波谷相遇处始终为振动减弱点.我们可据此,在干涉图样上,通过波峰或波谷叠加情况来判断质点振动情况.
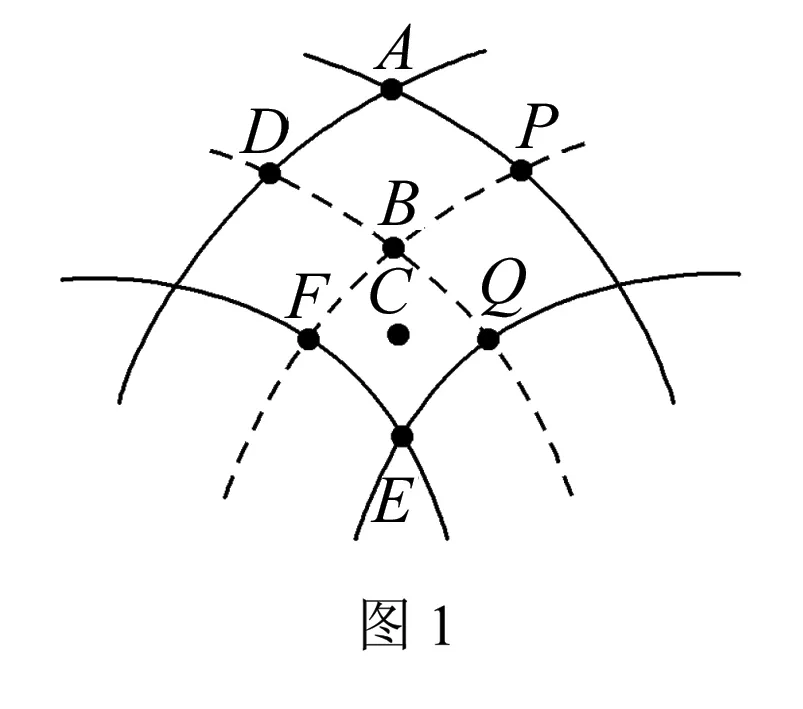
例1 如图1所示,两列相干水波进行叠加,实线和虚线分别表示在某一时刻它们所发出的波的波峰和波谷.关于图中所标的A、B、C、D、E、F、Q、P八点,C为B、E连线中点,下列说法中正确的有( ).
A.该时刻A质点振动最弱,B、E质点振动最强,C质点振动既不是最强也不是最弱
B.该时刻D质点振动最弱,B、C、E质点振动都最强
C.Q质点的振动始终是最弱的,A、B、C质点的振动始终是最强的
D.再过T/4后的时刻A、B、C三个质点都将处于各自的平衡位置,因此振动最弱
分析该时刻质点D、F、P和Q处于波峰与波谷相遇处,是振动减弱点,振动最弱;质点A、B、E分别处在波峰与波峰、波谷与波谷相遇处,是振动加强点,振动最强,这不难理解.但是质点C处不是波峰和波峰相遇、也不是波谷和波谷叠加,该怎样如何判断C振动强弱? 这可采用另一种方法“连线法”.
2.连线法
沿波的传播方向,将图1中几个振动加强点(A、B、C、E)连成一条直线,则该直线为振动加强区;若研究对象在该直线上,则为振动加强点,反之亦然.把沿波传播方向上相邻三个振动加强点连成一条线,该线就是振动加强区,C点在这条直线上,即在振动加强区,所以其为振动加强点.
对于例1,因描述振动强弱的物理量是振幅,而振幅不是位移.每个质点在振动过程中的位移是在不断改变的,但振幅是保持不变的,所以振动最强的点无论处于波峰还是波谷,振动始终是最强的.故例1答案应选B、C.
二、计算法
“计算法”是指根据质点与两波源位置的路程关系,通过计算来分析该质点位移叠加情况,来断定其振动强弱方法.常用的“计算法”包括“步调法”和“公式法”.
1.步调法
两列波发生干涉时,根据波的叠加原理,叠加区域的质点的位移为两列波单独传播到此处引起位移的矢量和.若两列波单独传播到某处引起位移分别为x1和x2,若该处质点位移x大小始终满足:|x|=|x1|+|x2|,则该处为振动加强点;若该质点位移x大小始终满足|x|=||x2|-|x1||,则该处为振动减弱点.
例2 在x轴上,有两列简谐横波分别沿正、负两个方向传播,波源的方向分别处在x=-2×10-1m及x=12×10-1m位置,波速均为v=0.4 m/s,振幅均为A=2 cm.图2是t=0时刻,两列波的图象和传播方向如图2所示,此刻平衡位置处于x=0.2 m和x=0.8 m的P、Q两质点刚开始振动,质点M的平衡位置处于x=0.5 m处.

(1)从t=0时刻起,两列波经多长时间相遇?
(2)质点M振动的振幅多大?其为振动减弱点还是振动加强点?
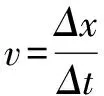
我们在使用“步调法”时,应了解:各质点的振动区域叠加,应包括振动位移叠加、振动速度的叠加和加速度的叠加.所以,要想采用“步调法”准确判断各质点在波的叠加区域中振动的合振动状况,就必须要考虑波的振动位移、速度等情况.
2.公式法

我们在使用“公式法”时,要格外注意两波源的振动步调是相同还是相反,然后在选择合适的公式.
当我们已经知道质点与两波源位置几何关系时,往往要采用“计算法”:若已知两波源的波形图时,可用“步调法”;若已知质点与两波源的的距离时,可用公式法.
总而言之,对于横波干涉中的振动加强点、振动减弱点的判断,我们可以根据具体条件,选择“观察法”或“计算法”来进行.
