利用导函数性质证明数列不等式问题

耿玉明

(广东省深圳市宝安中学 518101)

一、利用参数取值范围的临界值创设原型不等式

(1)用a表示出b,c;

(2)若f(x)≥lnx在[1,+)上恒成立，求a的取值范围；

思维特点先根据参数a的取值范围，取其临界值创设原型不等式，再通过对x赋值证明数列不等式.

二、 利用函数单调性结论创设原型不等式

例2 已知函数f(x)=2aln(1+x)-x(a>0).

(1)求f(x)的单调区间；

解(1)可求f(x)的单调递增区间为(-1,2a-1),单调递减区间为(2a-1,+)(略)

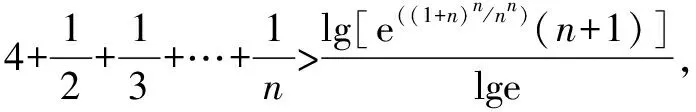
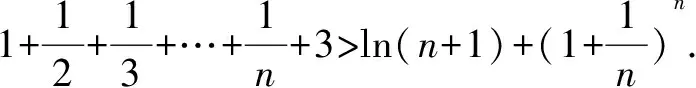
∴x∈(0,+)时,f(x)

思维特点先根据所求的单调区间，利用函数单调性在某一特定区间上创设原型不等式，再通过对x赋值证明数列不等式.

三、 利用函数的切线方程创设原型不等式

例3 已知函数f(x)=e1-x及g(x)=ln(3-x).

(1)求函数f(x)与g(x)的公切线方程;

(2)根据(1)结论，并由图可知ln(3-x)≤-x+2≤e1-x对于x∈R恒成立

思维特点先根据所求函数f(x)的切线方程，并借助于函数的凸凹性创设在某一区间上的原型不等式，再通过对x赋值证明数列不等式.