异构IWSN下对Sybil攻击源的定位∗
2019-03-26孙子文
孙子文,朱 颖
(1.江南大学物联网工程学院,江苏 无锡214122;2.物联网技术应用教育部工程研究中心,江苏 无锡214122)
工业无线传感器网络IWSN(Industrial Wireless Sensor Networks)[1]中,为节约成本,除少量节点带有自定位的GPS模块,大部分传感器节点则被随机分布在特定的检测区域,即节点的位置是未知的。IWSN在实际工作过程中会受到各种攻击和安全威胁,其中Sybil攻击是一种危害巨大,容易发起的基础攻击类型。受到Sybil攻击后,恶意节点违法地以多个身份出现,并发送错误信息,误导用户管理中心的决策。因此,在检测出Sybil攻击之后,对恶意节点及时进行定位是至关重要的。
IWSN中根据是否需要测距将定位算法分为基于测距定位算法和基于非测距定位算法[2]。基于测距的定位算法包括:信号到达角度AOA(Angle of Arrival)、到达时间TOA(Time of Arrival)、基于接收信号强度指示RSSI(Received Signal Strength Indication)等。非测距的定位算法主要包括:质心定位算法,距离矢量跳DV-Hop(Distance Vector-Hop)算法,近似三角形内点测试法APIT(Approximate Point-in-Triangulation Test)定位算法,多维比例图MDS-MAP(Multidimensional Scaling-Map)算法等。其中基于RSSI的定位技术具有定位精度高且无需额外的硬件设备等优点,使得RSSI定位算法成为一大研究热点。目前RSSI定位算法常用的是RSSI指纹定位算法[3]和基于RSSI测距的三边定位算法。Zhang G等人[4]采用RSSI指纹定位算法,在离线阶段,建立RSSI指纹数据库,在在线阶段,利用 K-近邻 KNN(K-Nearest Neighbor)匹配算法将采集到的RSSI值与指纹数据库中RSSI值进行匹配,最终选择出K个参考节点进行目标节点的质心定位算法。何青春等人[5]运用RSSI测距技术测量目标节点与已知参考节点之间的距离,随后利用三边测量定位算法得到目标节点坐标信息。然而RSSI易受环境影响,尤其在恶劣的工业环境下,测距误差较大,因此文献[6]进一步的改进,建立卡尔曼滤波器模型,在基于RSSI的定位算法进行测距时利用卡尔曼滤波器模型对通信节点之间的RSSI值进行平滑优化,使优化过的RSSI值更接近于理想测量值,从而来降低测距算法在测距过程中的误差,提高定位精度。在文献[7]中对采集到的RSSI值进行均值滤波,并基于RSSI进行泰勒级数展开定位算法,但在泰勒级数展开定位算法中初始值的选取未进行讨论。文献[8]中采用基于混合接收信号强度差RSSD(Received Signal Strength Difference)和到达时间差TDOA(Time Difference of Arrival)的最小二乘法定位算法,但对硬件要求高,且计算量大,定位精度不高。同时由于Sybil节点会篡改自身的信息来达到难以被定位的效果,导致大多数定位算法都不适用于直接定位攻击节点。如改进的RSSI指纹定位算法中,Sybil节点篡改接收到的RSSI值,使得无法与指纹数据库进行正确匹配。
Sybil攻击源的定位以攻击源的检测为基础,目前Sybil攻击检测方法中基于RSSI的检测方法凭借对节点硬件要求低,通信能耗少等优点,成为Sybil攻击检测的主流方法。文献[9]利用RSSI与节点ID的关联性,检测Sybil攻击。但改变节点发射功率则改变RSSI,所以仅利用关联性检测存在漏检问题。文献[10]利用不同节点接收的RSSI比值来解决RSSI的不可靠性,一个节点需要四个节点作为监测节点来进行检测,但监测节点会消耗大量能量,影响网络的生命周期。文献[11]采用一种基于异构IWSN的高能节点级、基站级的双层Sybil攻击检测方案,高能节点基于RSSI二次差值检测普通节点,基站根据高能节点的成功及不成功交互数量计算出信任值进行高能节点的检测。保证较低虚警率和漏警率的同时提高检测准确率,减少节点能耗,延长网络寿命。
文章借鉴TOA定位算法转化为TDOA定位算法的思想,在RSSI定位算法的基础上进行改进,实现了一种基于RSSD的定位算法[12],该算法可以定位具有未知传输信息的攻击节点的位置,适用于Sybil攻击源定位。通过参考节点采集攻击节点的RSSI值,并采用卡尔曼滤波对RSSI值进行预处理,先利用DV-Hop算法估计出未知参考节点的坐标;再根据RSSD测量值得到非线性方程组,因此对攻击节点定位问题转化为对非线性方程组的解算问题,通过最小二乘法估计方程组中攻击节点的初始值,利用泰勒级数展开法对攻击节点进行精确定位。
1 定位模型
假设整个网络分为普通节点和信标节点,其中信标节点通过GPS定位系统或者人工亲自部署等方法获取自身的位置信息,普通节点则是随机部署,因此位置是未知的。由于攻击源会篡改自身的信息,因此需要选取攻击节点通信范围内的部分节点作为参考节点参与定位。若被攻击的是信标节点,则节点位置已知,可以直接定位;若Sybil攻击发生在普通节点中,则需要进行攻击源定位。
在工业无线传感器网络中,假设需要定位的攻击节点的坐标为X=(x,y),参考节点的坐标为Xi=(xi,yi),i=1,2,…,N,N 为参考节点数。 如图 1 所示的攻击节点定位模型中,参考节点数N=4,在攻击节点的通信范围内选取出参考节点 X1,X2,X3,X4,其中参考节点X2是信标节点,另外三个参考节点X1,X3,X4是普通节点,此三个节点自身的位置也待估计。

图1 攻击节点定位模型
2 基于RSSD的攻击节点定位总体框架
当利用双层Sybil攻击检测方案[11]检测出攻击节点,攻击节点的ID会被发送至基站,基站接收到信息后,向整个网络发起对该攻击节点定位的命令。
基于RSSD的攻击节点定位主要分为三部分。第一部分,基站对参考节点的选择及位置估计。基站在攻击节点的所有邻居节点范围内选择出合适的参考节点参与定位,并对本身不是信标节点的参考节点利用DV-Hop算法进行位置估计。第二部分,参考节点对RSSI值的采集与预处理阶段。参考节点采集攻击节点发送数据包时的RSSI值后发送给基站,由基站采用卡尔曼滤波对所采集的RSSI值进行预处理。第三部分,基于RSSD的攻击节点的位置估计。根据接收信号强度差与传播距离之间的数学关系构建非线性方程组,采用最小二乘算法对攻击节点进行初步估计,再利用泰勒级数展开法进行精确定位。
2.1 基于RSSD的攻击节点定位架构图
如图2所示,是由参考节点的选择及位置估计、RSSI值的采集与预处理阶段、基于RSSD对攻击节点的初步定位及精准定位三个部分组成的攻击节点定位架构图。
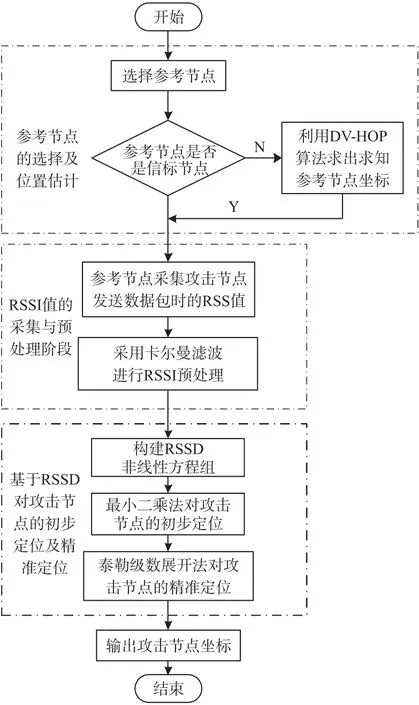
图2 攻击节点定位架构图
2.2 参考节点选择及位置估计
参与定位的参考节点数量越多,定位精确度越高,但所需的能量消耗也就越大,同时定位的时间也会增加,因此为了节约节点能耗以及减少定位时间,同时保证定位精度要求,需要选择出一些合适的参考节点来参与定位。
2.2.1 参考节点选择原则
在选取参考节点时遵循以下原则[13]:
①选取的节点应尽量均匀分布在攻击节点四周,也就是参考节点不能集中分布在攻击节点的一侧。理想状态下,所有参考节点连接起来所构造的区域应该以攻击节点为中心[14]。
②在节点同等均匀分布下,为了减少节点间传播过程中能量消耗,应选取距离攻击节点较近的参考节点,即所选参考节点到攻击节点的距离和最小[15]。
③所选择的参考节点的剩余能量不低于所有邻居节点的平均剩余能量。
根据构建的RSSD非线性方程组可以得到所需要的最少参考节点数量为4个。
2.2.2 基于DV-Hop算法对参考节点进行位置估计
DV-Hop算法是目前非测距定位算法中使用最广泛的定位算法之一,它具有实现简单、通信开销和计算量较小等优点,所以本文选用DV-Hop算法[16]对位置未知的参考节点进行位置估计。DV-Hop算法的基本思想是:用平均跳距乘以跳数,计算出信标节点到未知参考节点之间的距离,随后通过极大似然估计解出未知参考节点的坐标。位置未知的参考节点的坐标位置估计过程分为3个阶段。
第一阶段:获得最小跳数信息。每个信标节点将数据包{ID,位置,跳数(初始化为0)}发送给通信范围内的邻居节点,当邻居节点收到此数据包时,记录下到信标节点的跳数,然后跳数值加一继续转发给邻居节点。第二阶段:计算信标节点与未知节点之间距离。每个信标节点根据其到其他信标节点的最少跳数和自身坐标,计算出信标节点的平均跳距。所有信标节点将其平均跳距广播至整个网络中,未知参考节点将距离最近的信标节点的平均跳距作为自己的平均跳距。最后将平均跳距和跳数信息相乘获得未知参考节点到信标节点的距离。
第三阶段:求解未知参考节点的位置信息。根据未知参考节点已经记录了到各个信标节点的距离,利用极大似然估计计算出未知参考节点的坐标。
2.3 RSSI值的采集与预处理
攻击节点将数据包发送给通信范围内所有节点,其中参考节点就会采集接受数据包时的RSSI值,并将所采集到的RSSI值发送至基站,由基站采用卡尔曼滤波进行RSSI预处理。
2.3.1 参考节点对攻击节点RSSI值的采集攻击节点到参考节点的距离可表示为:
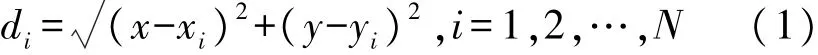
不考虑测量误差的理想环境下,根据阴影衰落模型,各参考节点接收到攻击节点的RSSI值可表示为:

式中:Pt是节点发送信号功率,γ是传播路径损耗指数,根据实际环境选取不同的值,K0是影响接收信号强度所有因素的总效应,如天线高度、天线增益和传输干扰等。将式(2)表示成对数正态分布形式

根据dB=10lg(X),在考虑噪声引起的测量误差情况下,RSSI值表示为[17]:

式中:e是高斯噪声,e~N(0,σ2)。
2.3.2 运用卡尔曼滤波对RSSI预处理
由于复杂的工业环境,存在电磁信号的多径效应和非视距传播以及大型工业设备的影响,RSSI信号强度并不稳定,存在一定的波动性,因此,不能将RSSI信号强度的一次测量值直接作为参考值,必须对RSSI值进行一定的预处理。
Kalman滤波是一种高效的滤波方法,它以最小均方误差为最佳估计标准,采取无线信号和环境噪声的状态空间模型,利用在上一状态下对现在的预测值和现状态下的测量值来代替对现状态的最佳估计,求出现在时刻的估计值。为了从一系列有噪声干扰的RSSI数据中用 Kalman滤波估计出理想RSSI值,首先,必须建立RSSI值系统模型并且用如下的线性微分方程来描述该模型:

式中:Ri(k|k-1)表示根据 k-1 时刻的 RSSI的预测值来预测 k时刻的 RSSI预测值,Ri(k-1|k-1)表示k-1时刻的最佳估计RSSI值,A和B是系统参数。当系统模型更新后,用T来表示更新的协方差:

式中:T(k|k-1)是 Ri(k|k-1)对应的协方差,T(k-1|k-1)是 Ri(k-1|k-1)对应的协方差,A′是 A 的转置矩阵,Q为系统过程噪声的协方差。
计算卡尔曼增益:

式中:H是系统模型参数,H′为H的转置,V为测量噪声的协方差。结合预测RSSI值和实际测量RSSI值,得到k时刻下最佳估计RSSI值Ri(k|k):

式中:Ri(k)是k时刻的实际RSSI测量值,Kg(k)是卡尔曼增益。
为了得到所有时刻下的最佳估计RSSI值,需要更新k状态下最佳估计RSSI值Ri(k|k)的协方差T(k|k),并将新的协方差代入下个迭代中,即将式(9)中的 T(k|k)代入式(6)中。

式中:I为1的矩阵,对于单模型单测量,I=1。假设k=2,3,…,kmax,当运行至 kmax时,所有时刻都得到最佳RSSI估计值,迭代结束。经过卡尔曼滤波,可有效地削弱由噪声等因素造成的RSSI的测量误差,达到提高测量精度的目的。
2.4 基于RSSD的攻击节点定位
基于RSSD的定位算法是通过测得攻击节点信号到达不同参考节点之间的信号强度强差,根据信号在空间传播的模型获得接收信号强度差与传播距离之间的数学关系构建非线性方程组,并对方程组进行解算估计攻击节点的位置坐标。泰勒级数展开法由于求解精度高,收敛速度快等优点是求解非线性方程组的有效方法,该算法对初始值有很强的依赖性,只有在初始值有一定的准确性的情况下才能有较快的收敛速度。因此文中采用最小二乘算法估计攻击节点坐标的初始值,再利用泰勒级数展开法进行精确定位,保证初始值的合理性,从而减少泰勒级数展开算法的复杂度。
2.4.1 基于最小二乘法的攻击节点初步定位
在式(4)RSSI值的表达式的基础上,参考节点之间的接收信号强度差RSSD可表示为[18]:
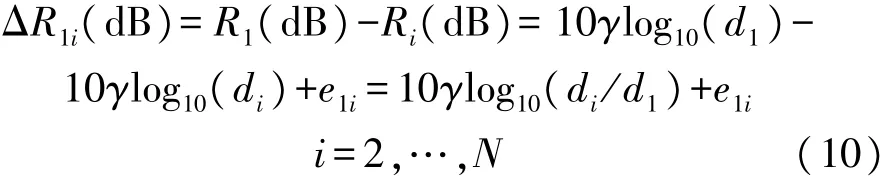
式中:e1i~N(0,σ2i+σ21),因此,RSSD 测量值与发射功率无关。由上式可得到参考节点Xi到攻击节点的距离di的表达式:
式中:Δ^R1i(dB)为RSSD的测量值。对式(1)左右两边同时平方,并代入左右两边同时平方的式(11)中,经过变换得到:
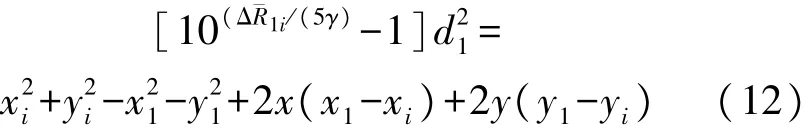
定义ξ1i=10Δ^R1i(dB)/(5γ)-1,攻击节点的估计位置坐标假设为^X=[^x,^y]T,则式(12)可以化简成矩阵的形式:

式中:
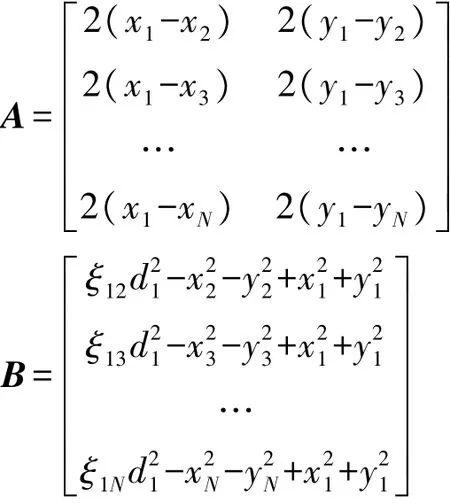
最后通过最小二乘估计:
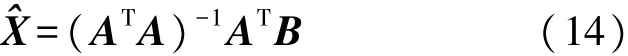
最小二乘法的特性以最小化误差平方之和来作为目标,保证了基于最小二乘法的粗定位可以收敛到真实位置附近,其次,将最小二乘法的值作为泰勒级数展开法的初始值之后,最终求出的目标位置估计值的门限值判定也保证了基于最小二乘法的粗定位可以收敛到真实位置。
2.4.2 基于泰勒级数展开法的攻击节点精准定位
泰勒级数展开法是一种迭代运算算法,根据参考节点之间的接收信号强度差RSSD建立非线性方程组,并转化成函数形式,将攻击节点的初始坐标代入,并在攻击节点处对其进行泰勒级数展开,获得最终攻击节点的位置估计[19]。
参考节点之间的接收信号强度差RSSD建立方程组如下所示:
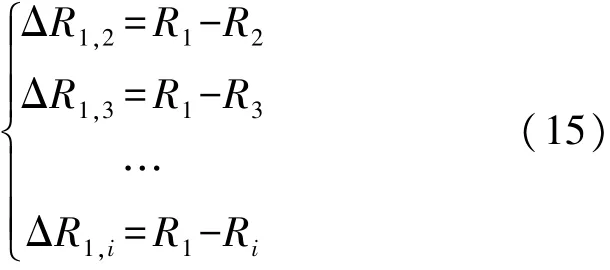
将式(2)以及式(1)代入式(15)中,得到如下非线性方程组:

将上式定义成函数形式:
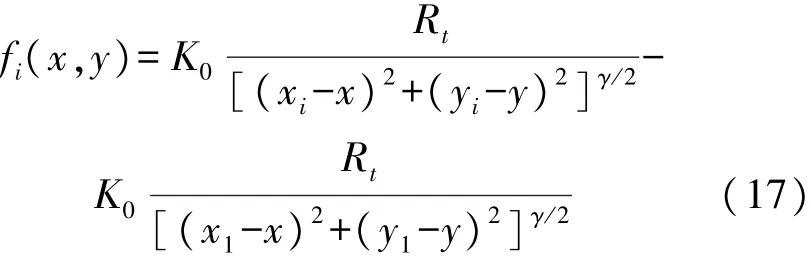
式中:i=1,2,…,N。
根据式(14)可以求得攻击节点的初始坐标为^X=[^x,^y]T,令x=^x+Δx,y=^y+Δy。对上式进行泰勒级数展开,可得
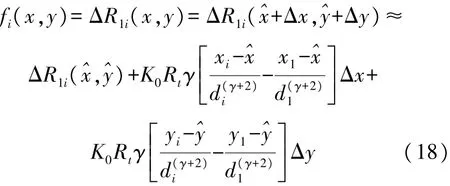
将上式转换成矩阵形式:

式中

使用最小二乘估计得到W的值
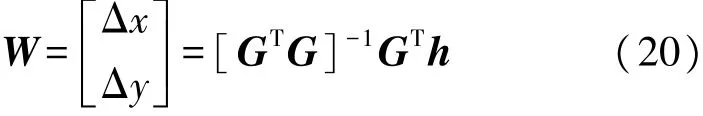
攻击节点的初始坐标为^X=[^x,^y]T,令x0=^x+Δx,y0=^y+Δy。且直至Δx,Δy足够小并满足一个预先设定的门限值 ε[20],使得|Δx|+ |Δy|<ε。 此时,得到最终攻击节点估计坐标X0=[x0,y0]T。
3 仿真与结果
为了对所研究的RSSD定位算法进行仿真验证,采用OPNET和MATLAB软件进行仿真实验,OPNET软件用于RSSI测量值的采集,MATLAB软件用于定位算法的实现。选择均方根误差RMSE(Root Mean Square Error)作为定位精度指标,将本文定位算法与文献[7-8]中的定位算法进行对比分析。
均方根误差RMSE的计算公式如下所示:

式中:n 为测量次数,Ln测量值与真实值的偏差,即攻击节点的最终估计坐标与实际坐标的偏差。
对采用卡尔曼滤波对RSSI预处理的作用进行仿真验证。首先,在OPNET软件仿真区域为150 m×150 m的范围内随机部署一个攻击节点以及九个邻居节点,考虑噪声情况下,采集其中一个节点的RSSI值共200组。再在MATLAB仿真软件中运行卡尔曼滤波算法,对采集到的200组RSSI值作为卡尔曼滤波的输入值,对RSSI值进行预处理后。卡尔曼滤波处理前后对比情况如图3所示,由图3可知,卡尔曼滤波算法收敛速度较快,在第100组数据时滤波后的RSSI值开始稳定在20 dBm左右。其中选择了150组到180组期间的RSSI值进行放大对比,滤波前,RSSI值波动范围为15 dBm~25 dBm,滤波后,RSSI值波动范围为19 dBm~21 dBm。可见,采用卡尔曼滤波对RSSI值进行预处理,对误差较大的值有很好的滤波作用,可以有效减少噪声干扰,达到去噪的效果,有利于提高定位精度。
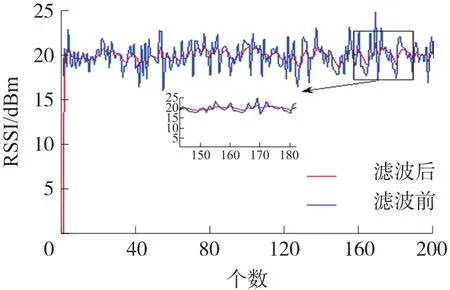
图3 卡尔曼滤波处理前后RSSI值对比图
验证采用DV-Hop算法对未知参考节点位置估计的必要性以及 DV-Hop算法的位置估计。在MATLAB中设仿真区域大小为1 000 m×1 000 m,随机部署300个未知节点和30个信标节点;普通节点通信半径为100 m,信标节点通信半径为150 m。节点分布情况如图4所示。

图4 节点分布情况

图5 节点间通信情况
节点间通信情况如图5所示。仿真计算出图5中未知节点通信区域内的信标节点平均数目为2.044 4,未知节点通信区域内的未知节点平均数目为8.592 6。可见,当需要对攻击节点进行定位时,攻击节点通信范围内的信标节点个数未达到定位时所需的参考节点个数最低要求4个,仅依靠信标节点来作为参考节点是不够的,为此,本文采用增加普通节点作为参考节点来对攻击节点进行定位,以有效地解决信标节点数量少的问题。
验证所选用的DV-Hop算法对位置未知节点的位置估计有很好的性能。假设在仿真区域内随机部署未知节点和信标节点,其中信标节点的密度为10%。定义未知节点归一化的相对定位误差为:

式中:MT为总节点的个数,MB为信标节点的个数,r为节点的半径,(xreal,i,yreal,i)为未知节点 i的实际坐标,(xtest,i,ytest,i) 为通过 DV-Hop 算法的估计坐标。表1为DV-Hop算法在不同总节数下的相对定位误差比较情况。

表1 DV-Hop算法相对定位误差情况
由表1可以看出DV-Hop算法对未知节点位置估计时有较低的定位误差,较好的定位性能,且随着节点个数增多,定位误差越小,但当总节点数达到300以后,定位误差处于稳定状态。
MATLAB软件仿真验证研究的RSSD定位算法的有效性。根据在OPNET软件中部署的一个攻击节点以及九个邻居节点的部署情况,在MATLAB中还原相同的部署,并在所有邻居节点中选择出四个最优参考节点。在相同条件下,不同门限值的选择会导致定位算法最终定位误差的差异,仿真中门限值设定为1.5,此时定位误差最小[20]。如图6所示,根据选择的四个参考节点对攻击节点进行定位。
与文献[7-8]中的Hybrid-LS定位算法和RSSI-TL定位算法进行定位性能对比,主要比较了不同算法定位攻击节点的均方根误差,仿真结果如图7所示。

图6 所选参考节点分布情况
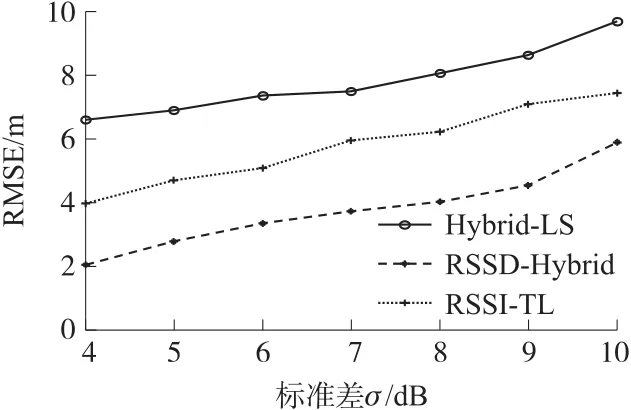
图7 不同算法的定位误差情况
由图7可知,当噪声标准差越大时,三种定位算法的定位均方根误差RMSE越大。当标准差在4 dB~10 dB之间变化时,Hybrid-LS定位算法[8]的RMSE在6m~10m之间变化;RSSI-TL定位算法[7]的RMSE在4 m~8 m之间变化;RSSD-Hybrid定位算法的RMSE在2 m~5 m之间变化。
表2列出了三种算法的时间复杂度,其中N表示样本数量,K为特征的数量。可以看出三种算法复杂度都属于线性级,是同一数量级,在复杂度方面略微增加。

表2 算法时间复杂度对比情况
因此,RSSD-Hybrid定位算法在复杂度方面略微增加,但定位精度要明显高于其他两种定位算法。
4 结论
根据工业无线传感器网络中被Sybil攻击的节点会篡改自身的信息导致难以被定位的问题,本文提出一种基于RSSD的定位估计算法。此方法中利用改进的DV-Hop算法估计出未知参考邻居节点的坐标,将攻击节点位置估计问题转化为对非线性方程组的解算问题,分别利用最小二乘法和泰勒级数展开法对攻击节点进行定位。整个定位算法可以有效地减少噪声的干扰,解决攻击源不配合定位和信标节点数量少的问题,显著提高节点定位精度。
