微小物体转动惯量测量机理与实现方法研究∗

王向军，王 凯

(1.天津大学精密测试技术及仪器国家重点实验室，天津300072；2.天津大学微光机电系统技术教育部重点实验室，天津300072)

转动惯量是刚体绕轴转动时惯性的度量，其值只取决于物体的形状、质量分布及转轴的位置[1－2]。刚体的转动惯量对于研究刚体的转动过程、掌握物体的三维转动规律有着重要的意义[3]。在航天领域，飞行器的飞行轨迹、姿态设计要考虑转动惯量的影响。在机械领域，机床上转台的转动惯量影响转台稳定性、精度[3]。在工业工程领域，电机的选择要考虑系统转动惯量的大小。总之，在许多领域转动惯量都是一个重要的静态参数。

转动惯量可以通过线摆法、扭摆法、复摆法等方法进行测量，其中线摆法在精密测量中不适用，只适合于粗测，多用于实验教学[4]；扭摆法通过选择合适的气浮平台可以实现对较大量程物体的精确测量(小于1%)，同时测量过程中，被测物体摆放在平台上，测量过程安全；复摆法要求被测物体和框架一起进行周期性摆动，所以要求被测物体的质量不能太重，同时根据物体的外形不同，测量过程可能不太安全。

目前，国内外主要通过扭摆法的原理，针对不同大小的物体设计出转动惯量测试系统[5]。但气浮平台的结构导致了装置环境要求高，辅助设备多，造价与维护费用高[6]。而且基于扭摆法的原理只能测量转动惯量，质心与转动惯量需要分开测量，使测量变得复杂繁琐[7－8]。同时气浮平台多是针对大尺寸大质量的物体，这与待测的100 g～500 g级别的被测物体质量差过大，用大量程的测量装置测量小物体，系统的误差对测量精度的影响较大，装置测量精度及稳定性较差。同时扭摆法需要人工放置被测物体，被测物体的轴心和平台的轴心之间的偏心也会影响测量精度，尤其是小物体小转动惯量的情况下。

本文针对微小物体转动惯量的测量问题，采用复摆法的原理，上文提到的复摆法的弊端，这里是针对小型物体，质量在100 g～500 g之间，满足被测物体质量小的条件，V型支承的设计使得被测物体放置后，确保质心与转轴的距离可以精测测量。同时因为被测件体积小，外形为圆柱，所以保证测量过程中相对安全。针对复摆法的原理，进行误差分析，并进行合理的机械设计以及误差补偿修正等手段消除误差影响。同时根据摆能确定重心的原理，将物体的质心测量与转动惯量测量结合到一个装置中，避免了两套装置反复装夹的繁琐操作以及带来的误差。实验结果表明测试装置在保证测量精度的前提下，具有快速高效、操作简单、成本低等特点。

1 测试装置的构成及工作原理

1.1 测试装置的构成

图1为转动惯量测量装置原理图。图2为转动惯量测量装置结构示意图。本装置主要由转动惯量测量装置、质心测量装置、光电计时模块、倾角测量模块、调平模块以及计算机等组成。转动惯量测量装置由复摆托架、托盘、V型支承、底座构成。质心测量装置由倾角仪、复摆托架构成。光电计时模块由遮光柱和光电计时器构成。调平模块由倾角仪和平衡螺母构成[9]。进行测量时，通过倾角仪和光电计时器获得倾角信息和复摆周期信息，把信息传递给计算机，通过计算机进行质心和转动惯量的计算。

图1 测量装置原理图

1.2 测试装置的工作原理

该装置的基本工作原理为：对于空载的装置，由电子天平测出托架质量m0。复摆的摆动方程：

当摆动角度很小时，认为托架在做简谐运动，得到托架的空载周期：

利用质量、长度、转动惯量已知的标准件对装置自身的参数进行标定，如托架质心到转轴的距离l0以及托架过转轴的转动惯量J0[10]。通过分析计算，得到装置参数：

式中：ms为标准件质量；ls为标准件质心到转轴的距离；Ts为标准件的复摆摆动周期。

对被测物体，首先通过电子天平测出质量m，计算得到被测物体质心到转轴的距离d[11]。分别2次放置被测物体，放置方向互相垂直，根据摆动方程：

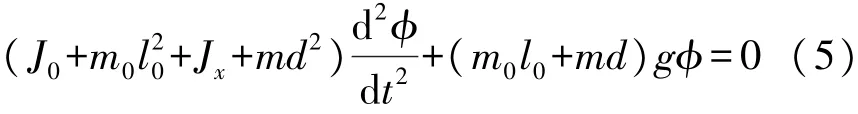
通过两次摆动周期的测量，得到被测物体极转动惯量和赤道转动惯量：

式中：T1为被测物体垂直转轴摆放时的摆动周期；T2为被测物体平行转轴摆放时的摆动周期；T0为系统空载时的摆动周期。

2 测试装置的结构设计及误差分析

2.1 结构参数设计

被测件参数参考值：ϕ60，300 g，150 mm。 需要测量微小物体的转动惯量，所以测试仪的质量尽量小，首先选取材料为铝合金。

支承设计。为使圆柱形被测件的轴线平行于工作面，采用V型支承。考虑被测件长度为150 mm，使V型支承均匀支撑被测件。取V型支承厚5 mm，相距80 mm，两个相对的支承的位置正好容纳被测件。相邻的支承要有一些间隙，取支承长28 mm，高19 mm。

图2 测量装置结构示意图

托盘设计。托盘置于横梁上，上面对称放置八个支承，托盘受到自身重力和被测件通过支承传递的压力的影响。将托盘视为受集中载荷以及受均匀载荷的悬臂梁，进行计算。此时悬臂梁的挠度为：

式中：F为集中载荷，取为5 N(最大被测物体质量)；l为梁的长度；b为集中载荷距固定端距离；E为铝的弹性模量；e为托盘厚度；q为悬臂梁本身均匀载荷；I为截面惯量。

梁的变形影响d的测量，根据误差忽略不计原则，d的误差由形变误差与d的测量误差组成，当一项误差大于另一个的3倍时，较小的误差可以忽略[12]。 这里为使形变忽略不计，取 Ymax＝0.2Δd，计算最小截面惯量I及托盘厚度。取宽度为100 mm，计算得托盘厚度最小为4.1 mm，取为5.0 mm。

横梁设计。横梁上放置托盘、V型支承和被测物体，同时受到自身重力的影响。将横梁视为受两个均匀载荷的简支梁进行计算。此时简支梁的挠度为：

梁的变形影响d的测量，同样根据误差忽略不计原则，取Ymax＝0.2Δd，计算横梁厚度和宽度。如表1所示计算得不同厚度对应的宽度。

表1 不同厚度对应的宽度

取厚度为10 mm，宽度为20 mm。

竖杆设计。如图3所示，根据之前设计的参数，画出框体的的结构简图。通过改变托架的杆长，分析极限误差的变化情况。

图3 结构图及误差变化

杆长为80 mm左右时，极限误差最小，约为真值的0.2%。杆长较短时，周期较小，影响周期的测量精度，且会影响装置稳定性，装置质心小的偏移会造成较大的倾角。同时考虑到质心测量时要进行被测件偏心摆放并进行倾角的测量，考虑最大偏移量为30 mm，复摆最大倾角10°，计算得杆长最小为130 mm时，满足最大倾角小于10°。所以综合考虑偏角与系统误差，选择杆长130 mm，误差约为真值的0.6%。

材料选择。选择不同材料进行分析，计算材料与极限误差的关系。

如图4所示，杆长在80 mm左右时，各密度取最小极限误差，随着杆长的增加，极限误差增大，且密度越大，误差越大。因此尽量选择密度小的材料，同时考虑到形变量要求及弹性模量的要求，拟采用1060铝合金。

图4 不同密度对应的误差

支承方式。考虑到装置摆动角度不大，速度较慢，载荷及装置质量较小。若采用滚动轴承的方式，滚动摩擦力太大，影响摆动的周期。选择气浮轴套，以空气作为润滑剂，用气膜将轴和轴套隔开，摩擦力可以忽略，适合于小负载情况。

调平装置。将倾角仪固定于框架之上，通过调节两侧的平衡螺母，使倾角仪保持水平。

计时装置。计时装置由遮光片和光电模块组成。光电模块由对射式红外激光器和LM393组成，直流5 V供电，输出高低电平。

2.2 系统误差分析

2.2.1 总体误差分析

考虑极转动惯量，因为自身标定的精度比测量精度高一个量级，因此忽略自身参数的误差对结果的影响。对式(6)进行微分得到：

得到极转动惯量的绝对误差公式：

同理得到赤道转动惯量的绝对误差公式。假设T、m、d的误差分布情况均为正态分布，极转动惯量的极限误差为：

根据式(12)，考虑误差构成：测量时间的误差ΔT1；测量质量的误差Δm；测量物体质心到摆轴距离的误差Δd；

2.2 .2 被测物体质偏影响分析

当实际质心与理想质心不重合时，称为质心偏移。设质心与摆轴的实际距离为d′，偏心为e，与垂直夹角为θ，但测得的距离为d，将d代入计算，会造成测量结果的偏差。由余弦定理，得到 d′＝以 d′代替式(6)、式(7)中的 d 进行计算即可。

当 θ＝0°或 180°时，考虑 Δd 的最大值，即 d′＝d－e或 d′＝d＋e，直接代入计算。 当偏心较小，测量存在误差时，需要将偏心作为误差项进行考虑。

如图5所示，偏心e在不同的尺度范围上，与误差呈现不同的相关性。在－3 cm到3 cm的范围内，误差和偏心近似为抛物线关系。在－0.2 cm到0.2 cm的范围内，误差与偏心有一定的线性关系，为后续的误差补偿提供了基础。

图5 偏心与相对误差的关系

将被测物体旋转180°，重新进行测量得出d″，jx″，T2。对测得的两个转动惯量求平均：

通过图6对比发现补偿后的测量结果大大减小了由偏心带来的转动惯量误差，通过旋转180°的两次测量，使质心偏移对转动惯量尽量产生相反的影响，通过对两次转动惯量测量结果的叠加，将相对误差从1.5%减小到0.4%，将质心偏移的影响基本抵消，即质心偏移基本不影响极转动惯量的测量。

图6 误差补偿效果

2.2.3 装置质偏影响分析

考虑到加工工艺的问题，框架不可能和设计时一样保持完全对称。框架的实际质心和转轴的连线与理想质心和转轴的连线存在一个θ角的偏差。框架静止时会相对竖直方向有一个θ的倾角。需要通过平衡螺母调节平衡，然后对装置进行标定，避免对测试结果产生影响。

2.3 刚度校验

对结构进行静力分析和刚度校验，设定好固定约束和负载，并将材料设定为铝合金，进行分析。

如图7所示，为装置的等效应力示意图。从图中看出托盘与横梁相接的地方是应力最大的区域，为9.5×105Pa，远远小于铝合金的屈服强度(2.8×107Pa)，符合设计要求。

图7 装置等效应力

如图8所示，为装置的等效弹性应变示意图，由等效应力得到等效应变。

图8 装置等效弹性应变

如图9所示，为装置的总应变示意图。从图中看出托盘部分是变形最大的区域，最大变形量为6.1×10－6m，小于 0.2Δd(1.0×10－5m)，符合设计要求。

图9 装置总应变

3 质心测量

考虑到重力场均匀，所以重心和质心重合，可以通过测量重心来测量质心。

以旋转轴为z轴建立坐标系。在空载时，通过调节平衡螺母使倾角仪保持水平。标定出空载的装置参数。将被测物体左端与V型支承对齐，此时托架会倾斜以保持平衡。通过倾角仪测出倾角θ。因为两个刚体的总质心在两个刚体各自质心的连线上，且总质心到各自质心的距离与两个刚体的质量成反比。所以有公式：m1l1＝m2l2。由三角形的相似原理，得到m1d1＝m2d2。直线的斜率与θ相关，根据点到直线距离公式以及三角函数的关系，得到被测物体质心经过的平面：

将被测物体右侧与V型支承对齐，通过倾角仪再次得到倾斜角度θ′，方向为负，以正值代入计算。得到质心经过的另一平面：

将平面向右平移，使该平面与上一个平面在同一个坐标系下，得到平移后的平面。

将被测物体旋转90°，后侧与V型支承对齐，根据倾角计算出质心经过的平面：

因为将被测物体旋转90°，所以该坐标系中的x方向对应旋转前坐标系中的－z方向，所以用－z代替x进行计算，将上述三个平面联立，可求出一点，即被测物体的质心。

4 测量实验与结果

利用装置对几个标准件进行测量。标准件1参数如下：m＝(96.620±0.005)g，重心位置[(46.40±0.02)mm，(0.00±0.02)mm，(0.00±0.02)mm]，Jx＝(0.229 0±0.000 1)kg·cm2，Jy＝(0.742 5±0.000 1)kg·cm2。测量结果如表2所示。

表2 标准件1的测量结果

标准件2参数如下：m＝309.00±0.005 g，重心位置[(60.00±0.02)mm，(0.00±0.02)mm，(0.00±0.02)mm]，Jx＝(2.325 5±0.000 1)kg·cm2，Jy＝(4.870 8±0.000 1)kg·cm2。测量结果如表3所示。

表3 标准件2的测量结果

标准件3参数如下：m＝497.09±0.005 g，重心位置(65.00±0.02 mm，0.00±0.02 mm，0.00±0.02 mm)，Jx＝(6.833 0±0.000 1)kg·cm2，Jy＝(10.417 5±0.000 1)kg·cm2。测量结果如表4所示。

标准件1通过扭摆法测量结果如表5所示，扭摆法中质心与转动惯量是两套系统分别测量。转动惯量测量范围0.1 kg·cm2到 100 kg·cm2，质心测量范围为10 g到1 kg。

表4 标准件3的测量结果

表５ 标准件１ 的测量结果

将测量值与真值进行比较得到测量精度，分析测量值得到重复性，如表6、表7所示。

表6 精度分析结果

表7 重复性分析结果

根据表6和表7可以发现，扭摆法测得的质心精度和重复性稍好于复摆法，扭摆法采用专门的质心测量系统进行测量，测量精度在0.6%以下，重复性在0.3%以下，复摆法测量精度在0.8%以下，重复性在0.6%以下。但是对于转动惯量的测量精度和重复性，复摆法的测量结果更优于扭摆法，复摆法的测量精度和重复性均在1.0%以下，扭摆法则在2%～3%。

5 结论

本文针对微小物体转动惯量的测量要求，搭建了复摆式的转动惯量测量装置，并介绍了装置的测量原理，分析了误差以及不同因素对测量结果的影响。之后进行装置的机械结构设计，并对结构进行了校验和优化。给出误差补偿方法以及综合测量质心和转动惯量的方案。最后进行实物加工以及装置搭建，校验装置的测量精度和重复性精度。校验结果证明：装置的质心测量精度为0.8%，装置的转动惯量测量精度为1.0%，装置的重复性精度为1.0%。满足对微小物体质心及转动惯量测量的稳定可靠、高精度、高重复性的要求。