一种磁性液体加速度传感器模型的参数辨识方法∗

杨永明，陈世强，李 强

(1.湖北民族学院新材料与机电工程学院，湖北恩施445000；2.湖北民族学院新材料成型及装备技术产学研中心，湖北恩施445000)

磁性液体传感器MFS(Magnetic Fluid Sensor)是一类新型传感器，这类传感器充分利用了磁性液体的流动性和磁性，具有磁可控性和阻力小等优点，能够应用于很多苛刻条件下，具有巨大的应用潜力[1－2]。磁性液体加速度传感器是近年来国内外学者研究较多的一种[3－4]。

磁性液体加速度传感器的磁芯(惯性质量)吸附磁性液体后，其等效半径、等效长度及等效相对磁导率都会发生变化，显然磁性液体对传感器参数的影响是不可忽略的，而加入的磁性液体体积可能存在误差，且长期使用时磁性液体存在挥发等问题，因此准确辨识上述三个参数对于磁性液体加速度传感器的校准和优化改进都很有必要。目前学者们对磁性液体传感器的研究主要集中在结构设计和优化上，对于参数辨识的相关研究工作尚不多见[5－7]。

目前参数辨识主要采用两类方法，即参数近似解法和基于优化算法的参数估计法。参数近似解法相对简单，但解出的参数误差一般较大，而基于优化算法的参数估计法误差较小，但存在求解耗时长等不足。在国内外参数辨识的研究中，不少学者采用遗传算法进行模型的参数辨识，文献[8]针对内嵌式永磁同步电机提出了一种基于遗传算法的参数识别方法，能同时辨识定子电阻、d轴电感、q轴电感和永久磁通量四个参数；文献[9]对车用锂离子电池建立了电化学模型，并利用遗传算法对模型进行了参数辨识；文献[10]讨论了利用多目标遗传算法进行液压机器人动力学模型的参数估计方法。遗传算法的编程实现比较复杂，此外，遗传算法诸如交叉率和变异率等的很多参数的选择依靠经验，若选取不合适将严重影响最终解的质量。因此遗传算法并不是求解本文模型的最佳方法。

文献[11]提出了一种利用新型自适应粒子群优化算法(APSO)，算法可寻找最优系统参数和最优控制参数，每个粒子根据粒子最佳记忆中获得的反馈对惯性质量进行动态调整，从而得到更快的收敛速度和更好的精度，同时减小计算负担。文献[12]提出了一种新的改进模糊粒子群优化算法(IFPSO)算法，通过最小化平方误差的平均值，对系统和控制器的参数进行了优化，利用模糊惯性权重，提高了粒子群的优化能力。上述两种算法在算法速度和算法精度上都作了优化，但未对算法早熟问题进行探讨，还有待进一步完善。文献[13]研究了混沌粒子群优化(PSO)在模糊系统参数估计中的应用，利用随机坐标的混沌变换提高了粒子的搜索能力。文献[14]提出了一种基于混沌粒子群的优化(PSO)算法，并成功应用到了电机的参数估计中，该算法利用逻辑图混沌初始化参数的值，同时考虑了惯性权重的调节，使算法取得了较好的收敛性能和搜索性能。上述两种算法通过引入混沌对粒子群进行初始化，提升了算法性能，但其采用的logistic映射在[0，1]的区间范围内分布不均匀，因此算法还有进一步提升空间。

本文通过对磁性液体加速度传感器模型进行研究，并参考上述算法，提出了一种改进混沌粒子群算法。为使初始解分布更加均匀，算法利用改进logistic映射对粒子群进行混沌初始化。此外，算法采用抛物线规律对迭代过程中的惯性权重进行实时调节，提高了算法效率。算法最终辨识出了磁性液体加速度传感器模型中磁芯的等效长度、等效半径及等效相对磁导率。

1 磁性液体加速度传感器模型

1.1 传感器输出电压与磁芯位移的关系

磁性液体加速度传感器的结构如图1所示，主要由惯性质量、壳体、检测线圈、回复磁铁组成。圆柱形磁芯(磁铁)两端吸附一定体积的磁性液体后形成惯性质量块，放入非导磁物质制成的圆筒壳体内，圆筒两端各布置一个回复磁铁。根据磁性液体的二阶悬浮原理，磁芯将悬浮起来。当壳体水平放置时，在回复磁铁的作用下，磁芯将处在正中间的位置。壳体中部缠绕的两个线圈用来检测惯性质量块的位置。

图1 磁性液体加速度传感器模型

传感器采用差动式传感器电桥将电感的变化量转换为电压的变化，该电压经放大电路放大及整流电路整流后输出。传感器最终输出电压可以表示为[15]

式中：U0为最终输出电压，Ui当电桥输入电压，w为输入电压频率，L0为线圈初始电感，R为线圈电阻，Av为放大电路、滤波电路及整流电路总的放大倍数，Δx为磁芯的位移量，r为线圈半径，l为线圈长度，μr为磁芯的等效相对磁导率，lc为磁芯等效长度，rc为磁芯等效半径。

利用式(1)，根据所测到的Δx和U0，运用改进混沌粒子群算法可对加速度传感器模型进行参数辨识。

图2 磁铁吸附磁性液体后的示意图

1.2 相关参数的计算

1.2.1 等效半径和等效长度的计算

磁铁吸附磁性液体后的示意图如图2所示，设球形磁性液体的半径为r，磁铁一端被磁性液体包裹部分的圆柱高度为h，圆柱形磁铁直径为d，设圆柱形磁铁底面圆圆心与球形磁性液体球心重合，则有

式中：V为磁铁一端吸附的磁性液体体积，V1为磁铁一端被磁性液体包裹部分的圆柱体积，V2为磁铁一端被磁性液体包裹部分的球缺体积。若已知磁性液体体积V和磁铁直径d则可求出球形磁性液体的半径r。可将两端吸附磁性液体的磁铁等效为一个底面半径为r的圆柱形磁芯，则根据体积的关系有

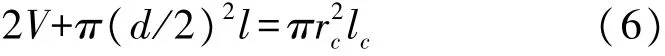
式中：rc和lc分别为等效圆柱形磁芯的半径、长度，l为磁铁的长度。求出半径r后即求出了rc，再根据式(6)即可求出lc。

1.2 .2 等效相对磁导率的计算

对于通电螺线管，线圈内的等效相对磁导率可以表示为[16－17]

式中f1和f2表示磁铁和磁性液体在容器内所占的体积分数，μB和μMF表示他们的相对磁导率。则根据 f1、f2及 μB、μMF即可求出等效相对磁导率 μr。

2 参数辨识

2.1 基本粒子群算法及混沌粒子群算法

基本粒子群算法(PSO)是模拟鸟群的捕食行为解决优化问题的一种算法，每个优化问题的解都是搜索空间中的一只鸟，称之为“粒子”，这些粒子通过迭代找到最优解，在每次迭代中，粒子通过两个极值来更新自己，即粒子本身找到的最优解(个体极值pbest)和整个种群目前的最优解(全局极值gbest)，更新公式如下[18－19]：

式中：vk是粒子的速度向量，xk是粒子的位置，pbestk是粒子本身所找到的最优解的位置，gbestk是整个种群目前找到的最优解的位置，w是惯性权重，c1、c2是学习因子。

混沌粒子群算法的基本思路是利用混沌算法的非线性、随机性、遍历性产生大量初始群体，从中择优选出质量较好的的群体，同时对当前粒子个体产生混沌扰动，使其跳出局部最优解区间。

2.2 改进Logistic映射

混沌粒子群算法一般采用Logistic映射产生初始群体，Logistic映射是一种数学形式上非常简单，动力学行为却极其复杂的非线性混沌系统。Logistic映射迭代公式为[20]：

式中：i＝0，1，2，…，系统在3.57＜μ≤4 时处于混沌状态。为扩大Logistic映射的参数范围，改善其动力学特性，不少研究者对Logistic映射的方程式做了改进，文献[21]提出了一种改进的logistic映射，其方程式为：

改进后的系统，有效地扩大了logistic映射处于混沌状态时μ的取值范围，在0＜μ≤4均处于混沌状态，且混沌序列在[0，1]区间上分布更加均匀。本文采用该改进的logistic映射对群体进行初始化，其中 k取值为 9。 μ＝4，z0＝0.2，i＝0，1，2，…，10 000时，改进前后的logistic映射zi的分布情况如图3所示，从图中可以看出，改进前zi的分布不均匀，在0和1.0附近密集，而在0.5附分散，而改进后zi的分布比较均匀。

图3 改进前后logistic映射的分布

2.3 适应度函数

适应度函数如式(13)所示。式中，Uoc为传感器输出电压的计算值，可根据式(1)由rc、ur、lc及其他已知参数表达出来；Uom为传感器输出电压的实际测量值。

2.4 早熟判断方法

在粒子群算法运行过程中，若群体适应度方差σ2等于零，且此时得到的最优解不是理论最优解或者期望最优解，则可判断算法进入局部最优，出现早熟收敛[22]。本文利用群体适应度方差判断算法是否陷入早熟，设定门槛值P，当σ2＜P时，判定算法陷入早熟。

2.5 权重调节方法

式8中包含w、c1、c2三个系数，其中惯性权重w对搜索效率的影响很大，在搜索最优解的过程中，应根据搜索过程对其进行实时调节，基本调节原则是在搜索初期进行全局搜索，而在搜索后期进行局部搜索，因此在搜索初期w应取较大值，而在搜索后期w应取较小值，为达到这一目的，本文根据迭代次数的变化对w进行自动调节，其调节公式如下

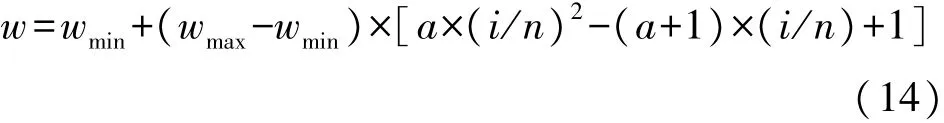
式中：a为经验值，取值范围为[0，1]，i为当前迭代次数，n为最大迭代次数，wmin为最小权重，wmax为最大权重。权重随i的增大而减小，且递减规律是一条抛物线。

2.6 参数辨识算法

在改进混沌粒子群算法(Improved Chaotic Particle Swarm Optimization)的实施过程中，利用改进logistic映射对群体进行初始化。为改善初始群体效果，需对初始群体进行筛选，基本筛选原则是群体在整个取值范围内分布比较均匀，且其适应度值在局部有较高质量。整个算法流程如图4所示，算法步骤如下：

Step 1 利用混沌初始化位置

设算法粒子数为m，要求解的参数个数为n，随机产生一个 n 维向量 z1＝(z11，z12，…，z1n)，其中每个分量取值范围为(0，1)，。利用改进的logistic映射计算出 z2，z3，…，zN，其中 N＝2 m，以载波形式优化变量：xij＝Xmin_j＋zij(Xmax_j－Xmin_j)，i＝1，2，…，N；j＝ 1，2，…，n.通过比较 f(xi)和 f(xm＋i)的大小，选出质量较好的 m 个 xi作为初始解，其中 i＝1，2，…，m。

Step 2 利用混沌初始化速度

随机产生一个 n 维向量 z′1＝ (z′11，z′12，，…， z′1n)，其中每个分量取值范围为(0，1)。利用改进的logistic映射计算出z′2，z′3，…，z′m，以载波形式优化初始速度：vij＝2zij∗Vmax－Vmax，i＝1，2，…，m；j＝1，2，…，n。

Step 3 初始化自身最优位置、自身最优适应度值、全局最优位置、全局最优适应度值

将每个粒子的初始位置作为自身最优位置pbest，根据每个粒子的初始位置计算各自的最优适应度值pfbest，从适应度值中找出最佳适应度值作为全局最优值gfbest，对应的最优位置作为全局最优位置gbest。

Step 4 更新各粒子速度和位置

计算出惯性权重w，并利用速度更新式和位置更新式更新各粒子的速度和位置，并限制在允许范围内。

Step 5 更新自身最优位置、自身最优适应度值、全局最优位置、全局最优适应度值

根据更新后的位置计算各粒子的当前适应度值，若当前适应度值优于自身最优适应度值，则用当前适应度值替换自身最优值，且用当前位置替换自身最优位置。若当前适应度值优于全局最优适应度值，则用当前适应度值替换全局最优值，且用当前位置替换全局最优位置。

Step 6 早熟判断

计算群体适应度方差σ2，当σ2＜P时，按Step 1和Step 2的方法更新粒子位置和速度，并重新进行迭代。

Step 7 算法结束

若全局最优值达到精度要求或者迭代次数达到规定次数则数据全局最优值和全局最优位置，算法结束，否则跳转到Step 4。

图4 算法流程

3 实验与评估

3.1 实验环境

实验过程中，将传感器上的两个线圈与变压器接成电感传感器电桥，供桥电源由普源DG2041A型函数发生器提供，电桥输出信号经放大、整流、滤波后由北京阿尔泰公司的USB2813A型数据采集卡采集，计算机端采用Labview软件编写程序对信号进行处理。传感器模型参数的选取为：圆柱形惯性质量(钕铁硼永磁铁)半径为5 mm，长20 mm，相对磁导率为1.05；圆柱形壳体半径为8 mm，长60 mm；回复磁铁外径19 mm，内径14 mm，高5 mm，回复距离120 mm；两个线圈匝数为2 000，线径为0.21 mm；电阻为90 Ω；线圈骨架内径20 mm，外径40 mm，单个骨架长20 mm。实验过程中采用两种磁性液体，一种为化学共沉淀法制备的煤油基Fe3O4磁性液体(记为1＃磁性液体)，另一种为Massart法制备的水基CoFe2O4离子型磁性液体(记为2＃磁性液体)，两种磁性液体参数如表1所示。每种磁性液体进行四次实验，四次实验中磁体每端吸附的磁性液体体积分别为 0.5 mL、0.75 mL、1.0 mL 和 1.25 mL，根据上述参数及式(2)至式(7)，可求出不同磁性液体体积下待求参数的参考值，如表2所示。

表1 磁性液体物理性能参数

3.2 实验结果与分析

为验证改进混沌粒子群算法在传感器模型参数辨识中的有效性，利用所测到的传感器输入和输出数据对传感器进行了参数辨识，表2中分别给出了磁体每端吸附不同磁性液体及不同体积时，粒子群算法、混沌粒子群算法及改进混沌粒子群算法运行100次后辨识出的参数，表3给出了不同算法辨识出的参数的相对误差。从中可以看出改进混沌粒子群算法辨识出的参数最接近参考值，相对误差小于0.85%。

图5显示了磁体每端吸附不同磁性液体及不同体积时，各种算法辨识结果所对应的磁芯位移与输出电压之间的曲线和参考曲线。从图中可以看出，在不同情况下，采用改进混沌粒子群算法辨识出的参数所对应的曲线与参考曲线的拟合度最好。

表2 参考值及辨识出的参数值

表3 不同算法辨识出的参数相对误差 单位：%

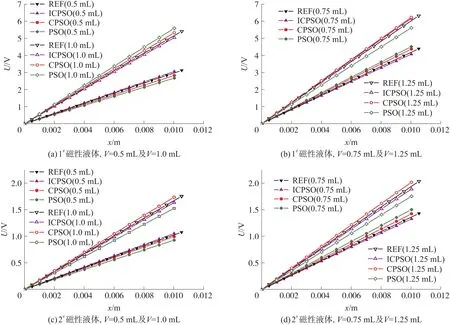
图5 磁芯位移与输出电压曲线

为进一步说明各曲线与参考曲线的拟合度，在磁芯位移范围内均匀地取100个点，利用归一化均方根误差NRMSE(Normalized Rootmean Square Error)适应度值来评价曲线的拟合度，不同情况下归一化均方根误差适应度值如表4所示，从表中可以看出，采用改进混沌粒子群算法时辨识曲线与参考曲线的拟合度在94.37%以上。

综上，所选的两种磁性液体在不同实验条件下均能较准确地辨识出磁芯的等效长度、等效半径及等效相对磁导率，说明改进混沌粒子群算法在磁性液体加速度传感器参数辨识中是有效的。同时可以看出，选用水基CoFe2O4磁性液体时辨识出的参数误差更小且辨识曲线与参考曲线的拟合度更高。分析发现在磁性液体的物理性能参数中，相对磁导率是影响辨识精度的主要参数，其主要原因在于：整个磁芯由磁体和磁性液体组成，相对磁导率分布不均匀(磁性液体和磁体的相对磁导率不同)，会导致磁芯移动时两个感应线圈的自感系数产生不均匀变化，而本文在计算传感器输出时是将磁芯等效为磁导率均匀的磁芯，这会给传感器输出的计算值带来一定误差。显然，磁性液体和磁体的相对磁导率相差越小，磁芯相对磁导率分布越均匀，而本文所选水基CoFe2O4磁性液体和磁体的相对磁导率相差更小，因此所辨识出的参数误差也更小。

表4 归一化均方根误差适应度值

4 结论

为准确辨识出磁性液体加速度传感器模型中磁芯的等效长度、等效半径及等效相对磁导率，提出一种改进混沌粒子群算法，算法利用改进logistic映射对粒子群进行混沌初始化，并采用抛物线规律对迭代过程中的惯性权重进行实时调节。结果表明，该方法辨识出的参数相对误差小于0.85%，且辨识曲线与参考曲线的拟合度在94.37%以上，说明该方法在磁性液体加速度传感器参数辨识中是有效的。选用不同的磁性液体时，相对磁导率是影响辨识精度的主要参数，减小磁性液体和磁体之间相对磁导率的差值，可提高参数辨识精度。