涂覆石墨烯的椭圆形电介质纳米线光波导的模式特性分析*
2019-03-26程鑫薛文瑞卫壮志董慧莹李昌勇
程鑫 薛文瑞† 卫壮志 董慧莹 李昌勇
1) (山西大学物理电子工程学院, 太原 030006)
2) (山西大学激光光谱研究所, 量子光学与光量子器件国家重点实验室, 太原 030006)
3) (山西大学, 极端光学协同创新中心, 太原 030006)
设计了一种涂覆石墨烯的椭圆形电介质纳米线光波导. 采用分离变量法, 在椭圆柱坐标系中, 借助Mathieu函数, 得到了色散方程. 通过数值求解色散方程, 可以得到模式的有效折射率和场分布, 从而得到模式的传播长度. 研究了工作波长、结构参数以及石墨烯的费米能对模式特性的影响, 并给出了前五个模式的品质因数. 计算表明, 当波长从 4.3 增加到 8.8 , 这 5 个模式的有效折射率的实部减小, 基模和一阶模的传播长度增大, 二阶模的传播长度先增大后减小. 当改变纳米线结构参数半长轴和半短轴时, 对基模和一阶模的模式特性影响较小, 对二阶模的模式特性影响较大. 当石墨烯的费米能从0.45 eV增加到0.72 eV时, 有效折射率的实部减小, 传播长度可以达到2 左右. 分离变量法得到的结果与有限元方法得到的结果完全一致. 本文工作可以为基于涂覆石墨烯的电介质纳米线的光波导的设计、制作和应用提供理论基础.
1 引 言
表面等离子激元(SPPs)是一种电磁表面波.利用SPPs可以在亚波长范围内约束和控制光波的传输, 因此SPPs在纳米光子学中有着重要的应用前景[1].
石墨烯是一种由碳原子紧密堆积而成的蜂巢晶格的二维结构[2-4], 在其表面可以激发SPPs[5].石墨烯有三大优点: 超强的模式约束、相对较大的传播长度、可调的化学势和载流子迁移率[6]. 因此,在中红外到太赫兹波段, 石墨烯是优选的材料. 许多学者对基于石墨烯的各种结构的波导进行了研究, 例如基于石墨烯带的平板波导[7,8]、基于石墨烯的楔形/槽形波导[9,10]和基于石墨烯的混合波导[11-13]等. 与传统的基于贵重金属的表面等离子波导相比, 基于石墨烯的表面等离子波导有两个优点: 欧姆损耗低、对电磁场有较强的亚波长约束能力[7].
近年来, 为了传输中红外到太赫兹波, 涂覆石墨烯的电介质纳米线波导受到了人们的关注. 这类波导是在单根或多根对称、非对称分布的圆柱形电介质纳米线上涂一层或多层石墨烯构成. 与平板石墨烯波导相比, 这类波导不存在边缘损耗. 研究表明, 在涂覆单层石墨烯的单根圆柱形纳米线波导中, 通过调节工作波长, 可以实现单模工作[6]; 在涂覆单层石墨烯的方形纳米线波导中, 可以实现较小的归一化模式面积[14]; 在涂覆双层石墨烯的单根圆柱形纳米线波导中, 可实现深度亚波长约束[15]; 在涂覆多层石墨烯的单根圆柱形纳米线波导中, 可进一步增强模式的束缚性[16]; 在涂覆单层石墨烯的并行纳米线波导的狭缝区域, 有明显的场增强效应及超强的梯度力[17,18]; 在涂覆单层石墨烯的非对称并行纳米线波导中, 可以灵活调节模式的传输性能[19].在涂覆双层石墨烯的纳米并行线间狭缝区, 可以得到更高的场增强[20]. 在涂覆单层石墨烯的三根并行纳米线波导中, 可以灵活调节模式的有效折射率及传播长度[21]. 在低太赫兹频率下, 利用石墨烯单层和纳米结构石墨烯超表面可以使电介质和金属椭圆柱隐身[22].
本文设计了一种涂覆单层石墨烯的单根椭圆形电介质纳米线光波导, 采用分离变量法, 对这种波导所支持的模式进行研究. 就工作波长、结构参数以及石墨烯的费米能对模式特性的影响进行了分析. 为了验证分离变量法结果的正确性, 与有限元法(FEM)的结果进行了对比. 这种波导有望在中红外到太赫兹波的保偏传输方面得到应用[23-25].本文设计的涂覆石墨烯的椭圆形电介质纳米线光波导利用了表面等离子共振效应. 由于表面等离子激元(SPPs)的传输距离在波长量级, 适用于短距离传输, 在存储器[26]、光操控[27]和光子器件的高密度集成[28]等领域有着潜在的应用前景.
2 理论模型与计算方法
涂覆石墨烯的椭圆形电介质纳米线光波导的横截面如图1所示. 它是在相对介电常数为的椭圆形电介质纳米线的表面涂覆单层石墨烯材料构成, 背景介质是空气, 介电常数为. 假设,. 波导结构的半长轴为, 半短轴为, 椭圆的左、右两个焦点分别为和, 半焦距为.石墨烯的表面电导率与工作角频率、环境温度和石墨烯的费米能有关, 由带内电导率和带间电导 率两部分 构 成 (), 并可以通过Kubo公式得到[29]:
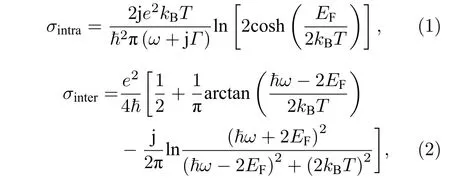
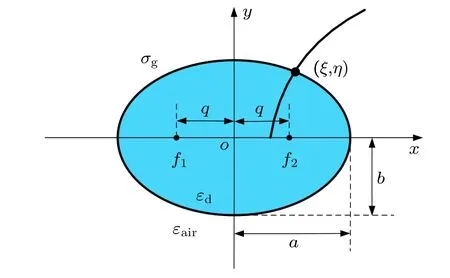
图1 涂覆石墨烯的椭圆形电介质纳米线光波导的横截面示意图Fig. 1. Cross section of the optical waveguide based on graphene-coated elliptical dielectric nanowire.



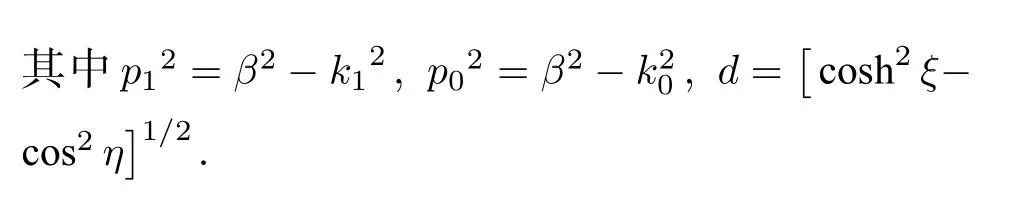

由(7)式可以得到一个奇次的线性代数方程组:

3 结果及分析
图2(a)—图 2(e)分别给出在 a = 110 nm,b = 80 nm,和的情况下, 该波导支持的五个最低阶模式(依次命名为Mode 1,Mode 2, Mode 3,和 Mode 5)对应的 z 方向电场分量分布, 图2(f)—图2(j)为其对应的电场强度分布. 可以看出, 场集中分布在石墨稀涂层附近. 其中 Mode 1 为基模, Mode 2 和 Mode 3为一阶模, Mode 4 和 Mode 5 为二阶模. Mode 1,Mode 3 和 Mode 5 为偶模, Mode 2 和 Mode 4 为奇模.
图3(a)—图 3(c)分别给出了在 a = 110 nm,b = 80 nm 和的情况下, 有效折射率实部、传播长度和品质因数FOM与波长之间的依赖关系. 图中实线为 FEM 的模拟结果, 点线为分离变量法得到的计算结果, 下文中均用该方法标注. 从图3中可以看出, 随着波长的增大, 前五个模式的有效折射率的实部都单调减小,其中 Mode 1, Mode 2 和 Mode 3 的有效折射率的实部下降较慢, 而 Mode 4 和 Mode 5 的有效折射率的实部下降较快. 随着波长的增大, Mode 1,Mode 2 与 Mode 3 的传播长度单调增加, 而 Mode 4和Mode 5的传播长度先增大后减小. 随着波长的增大, 品质因数FOM先增大再逐渐减小, 其中Mode 1, Mode 2 和 Mode 3 的品质因数下降较慢,而 Mode 4 和 Mode 5 的品质因数下降较快. 因为品质因数FOM越大, 波导的传输性能越好[35], 在所选参数范围内, Mode 2 的品质因数最大, 所以Mode 2的传输性能最好.
上述现象可以通过场分布来解释. 以Mode 5 为例, 图 4 给出了, 7.5 和 8.5三种情况下电场强度分布的对比图. 从图中可以看出, 当时, 场被紧密地约束在石墨烯涂层附近,场与石墨烯涂层之间的相互作用强, 此时波导对场的约束性非常强, 能量分布集中, 但模式的传输损耗较大, 传播长度较小. 当时, 场分布扩散至电介质纳米线和空气中, 场与石墨烯涂层之间的相互作用变弱, 波导对场的束缚性变弱, 传输损耗减小, 因而传播长度增大. 当时, 虽然场分布扩散到电介质纳米线和空气中的越来越多,波导对场的束缚性变弱, 但是石墨烯涂层附近的场的强度增强, 场与石墨烯之间的相互作用变强, 传输损耗增大, 因而传播长度减小.

图2 在 a = 110 nm, b = 80 nm, 和 的情况下, 前五个模式对应的 z 方向电场分量 (a)—(e)与电场强度 分布图 (f)—(j)Fig. 2. The z direction electric field component (a)—(e)and electric field intensity (f)—(j) corresponding to the first 5 modes with a = 110 nm, b = 80 nm, and .
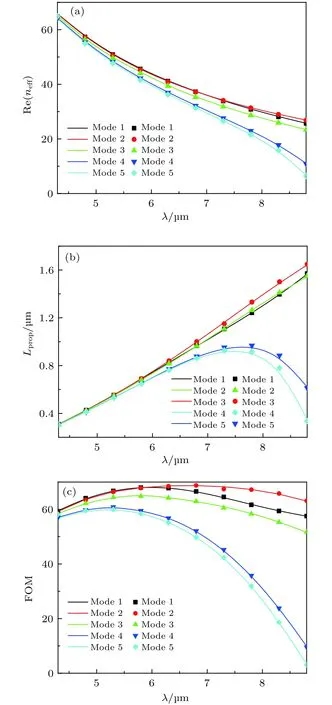
图3 在 a = 110 nm, b = 80 nm 和 的情况下, 有效折射率实部(a), 传播长度(b)和品质因数(c)与波长的关系Fig. 3. Dependence of the real part of the effective refractive index (a), propagation length (b) and FOM (c) on the wavelength with a = 110 nm, b = 80 nm and .
图5 (a)—图 5(c)分别给出了在 b = 90 nm,部、传播长度和品质因数FOM与半长轴a的关系. 从图中可以看出, 当半短轴b的长度一定时, 随着a的增大, 前5个模式的有效折射率的实部逐渐增大, 其中Mode 3的有效折射率的实部变化极小, Mode 1 和 Mode 2 的有效折射率的实部增长速度比 Mode 4 和 Mode 5 的慢. 随着a 的增大, Mode 1 的传播长度基本不变, Mode 3的传播长度缓慢减小, Mode 2, Mode 4 和 Mode 5的传播长度缓慢增大. 随半长轴 a 的增大, Mode 1和 Mode 2 的品质因数增加较慢, Mode 3 的品质因数缓慢减小, Mode 4 和 Mode 5 的品质因数增加较快. 在所选参数范围内, Mode 2 的品质因数最大, 传输性能最好.

图4 在 a = 110 nm, b = 80 nm 和 的情况下,不同波长时Mode 5的电场强度 分布图 (a) ;(b) ; (c)Fig. 4. The distribution of the electric field intensity of the Mode 5 with different wavelength when a = 110 nm,b = 80 nm and : (a) ; (b) ;(c) .
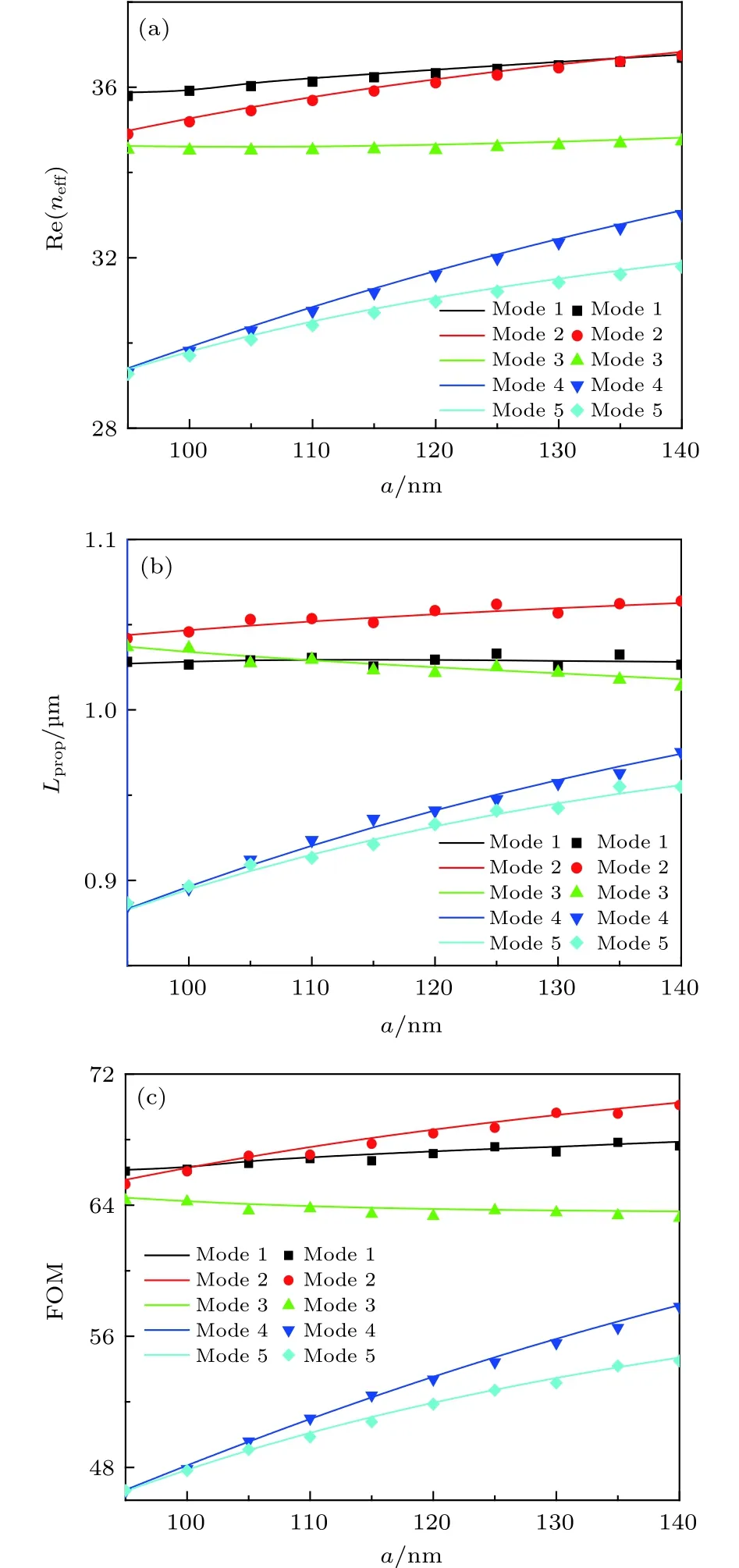
图5 b = 90 nm, 和 的情况下, 有效折射率实部(a), 传播长度(b)和品质因数(c)与半长轴a的关系Fig. 5. The real part of the effective refractive index (a),propagation length (b) and FOM (c) as a function of semimajor axis when b = 90 nm, and .
上述现象可以通过场分布来解释. 以Mode 5为例, 图 6 给出了当 b = 80 nm,,时, a = 100, 120 和 140 nm 情况下的电场强度分布对比图. 从图中可以看出, 当 a = 100 nm 时,石墨烯椭圆环的周长较小, 场被约束在石墨烯椭圆环附近, 场与石墨烯之间的相互作用强, 模式的传输损耗大, 传播长度小. 当 a = 120 nm 时, 石墨烯椭圆环的周长变大, 场分布的范围扩大, 在半长轴增大的过程中, 左右花瓣对应的场的强度基本保持不变, 而上下花瓣对应的场的强度减小, 场与石墨烯之间的相互作用变弱, 传输损耗减小, 因而传播长度增大. 当 a = 140 nm 时, 石墨烯椭圆环的周长进一步变大, 场分布进一步扩散, 在半长轴增大的过程中, 左右花瓣对应的场的强度基本保持不变, 而上下花瓣对应的场的强度进一步减小, 场与石墨烯之间的相互作用进一步变弱, 传输损耗进一步减小, 因而传播长度进一步增大.
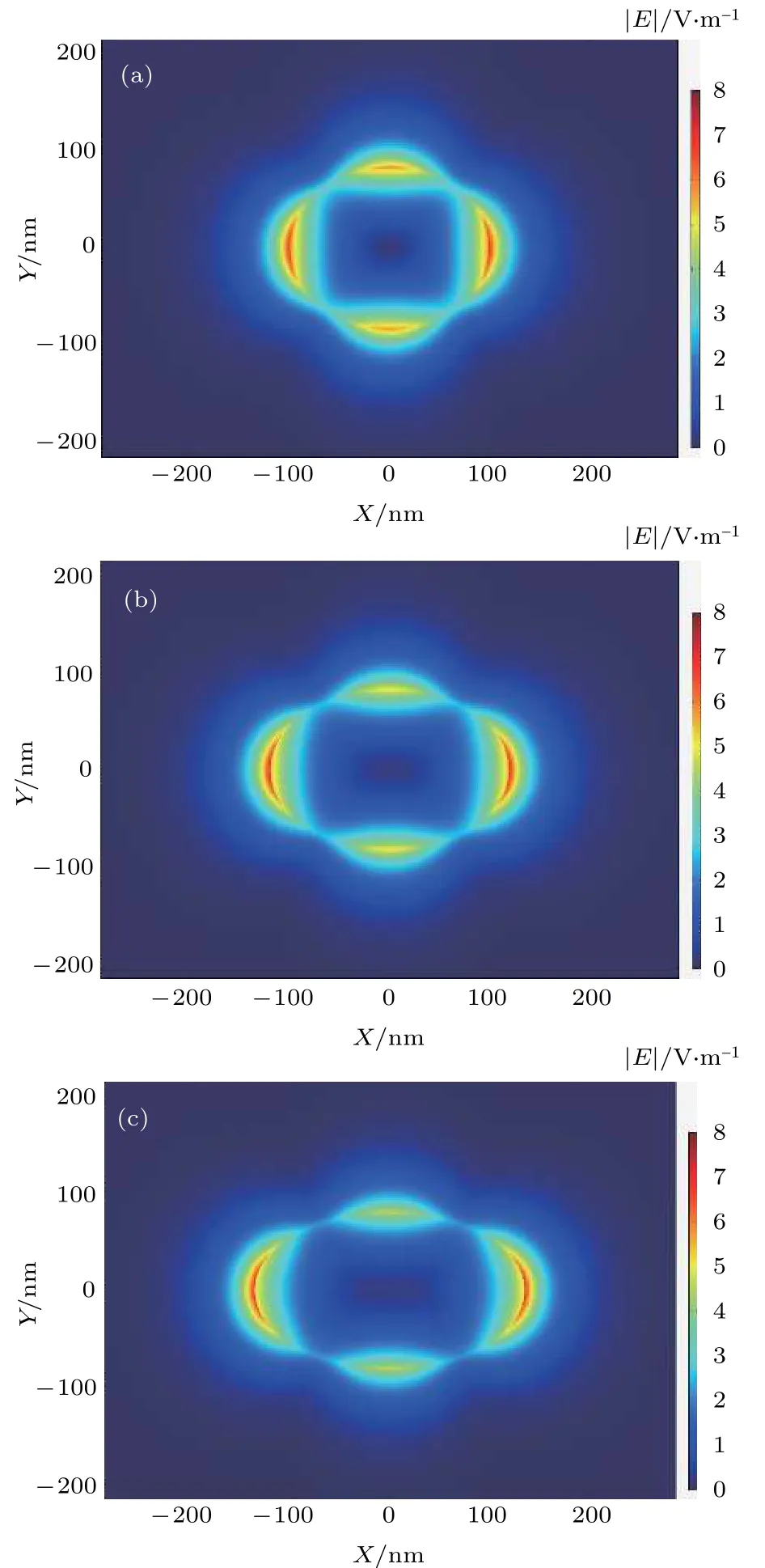
图6 在 b = 80 nm, 和 的情况下,半长轴长度取不同值时Mode 5的电场强度 分布图(a) a = 100 nm; (b) a = 120 nm; (c) a = 140 nmFig. 6. The distribution of the electric field intensity of the Mode 5 with different length of semi-major axis when b = 80 nm, and : (a) a = 100 nm;(b) a = 120 nm; (c) a = 140 nm.

图 7 当 a = 110 nm, 和 时, 有效折射率实部(a), 传播长度(b)和品质因数(c)与半短轴b的关系Fig. 7. The real part of the effective refractive index (a),propagation length (b) and FOM (c) as a function of semiminor axis when a = 110 nm, and .
图7 (a)—图 7(c)分别给出了在 a = 110 nm,部、传播长度和品质因数FOM与半短轴之间的关系. 从图 7中可以看出, 当半长轴a 的长度一定时, 随着半短轴 b 的增大, Mode 1,Mode 3, Mode 4 和 Mode 5 的有效折射率的实部逐渐增大, 其中 Mode 5 的增加速度最快, Mode 2的有效折射率的实部缓慢减小. 随着半短轴b的增大, 除Mode 2外其余4个模式的传播长度都在增大, 其中 Mode 5 的增长速度最快. 随着半短轴b的增大, 除Mode 2外其余4个模式的品质因数FOM 都单调增大, 其中 Mode 1 和 Mode 3 的品质因数增加较慢, Mode 5 的品质因数增加较快. 在所选参数范围内, 当 b < 95 nm 时, Mode 2 的品质因数最大, 传输性能最好, 当> 95 nm 时,Mode 1的品质因数最大, 传输性能最好.

图8 在 a = 110 nm, 和 的情况下,半短轴长度取不同值时Mode 5的电场强度 分布图(a) b = 65 nm; (b) b = 85 nm; (c) b = 105 nm.Fig. 8. The distribution of the electric field intensity of the Mode 5 with different length of semi-minor axis when a = 110 nm, and : (a) b = 65 nm;(b) b = 85 nm; (c) b = 105 nm.
上述现象可以通过场分布来解释. 以Mode 5为例, 图 8 给出了 b = 65, 85 和 105 nm 情况下的电场强度分布对比图. 从图中可以看出, 当 b =65 nm 时, 石墨烯椭圆环的周长较小, 场被约束在石墨烯椭圆环附近, 场与石墨烯之间的相互作用较强, 模式的传输损耗大, 因此传播长度小. 当 b =85 nm 时, 石墨烯椭圆环的周长变大, 场分布逐渐扩散, 左右花瓣对应的场的强度有所减弱, 而上下花瓣对应的场的强度基本保持不变, 场与石墨烯之间的相互作用变弱, 传输损耗减小, 因而传播长度增大. 当半短轴增大至 105 nm时, 石墨烯椭圆环的周长进一步增大, 场分布的扩散范围也进一步变大, 左右花瓣对应的场的强度进一步减弱, 而上下花瓣对应的场的强度基本保持不变, 场与石墨烯之间的相互作用进一步减弱, 传输损耗进一步减小,因而传播长度也进一步增大.

图9 当 a = 110 nm, b = 80 nm 和 时, 有效折射率实部(a), 传播长度(b)和品质因数(c)与费米能的关系Fig. 9. The real part of the effective refractive index (a),propagation length (b) and FOM (c) as a function of Fermi energy when a = 110 nm, b = 80 nm and .
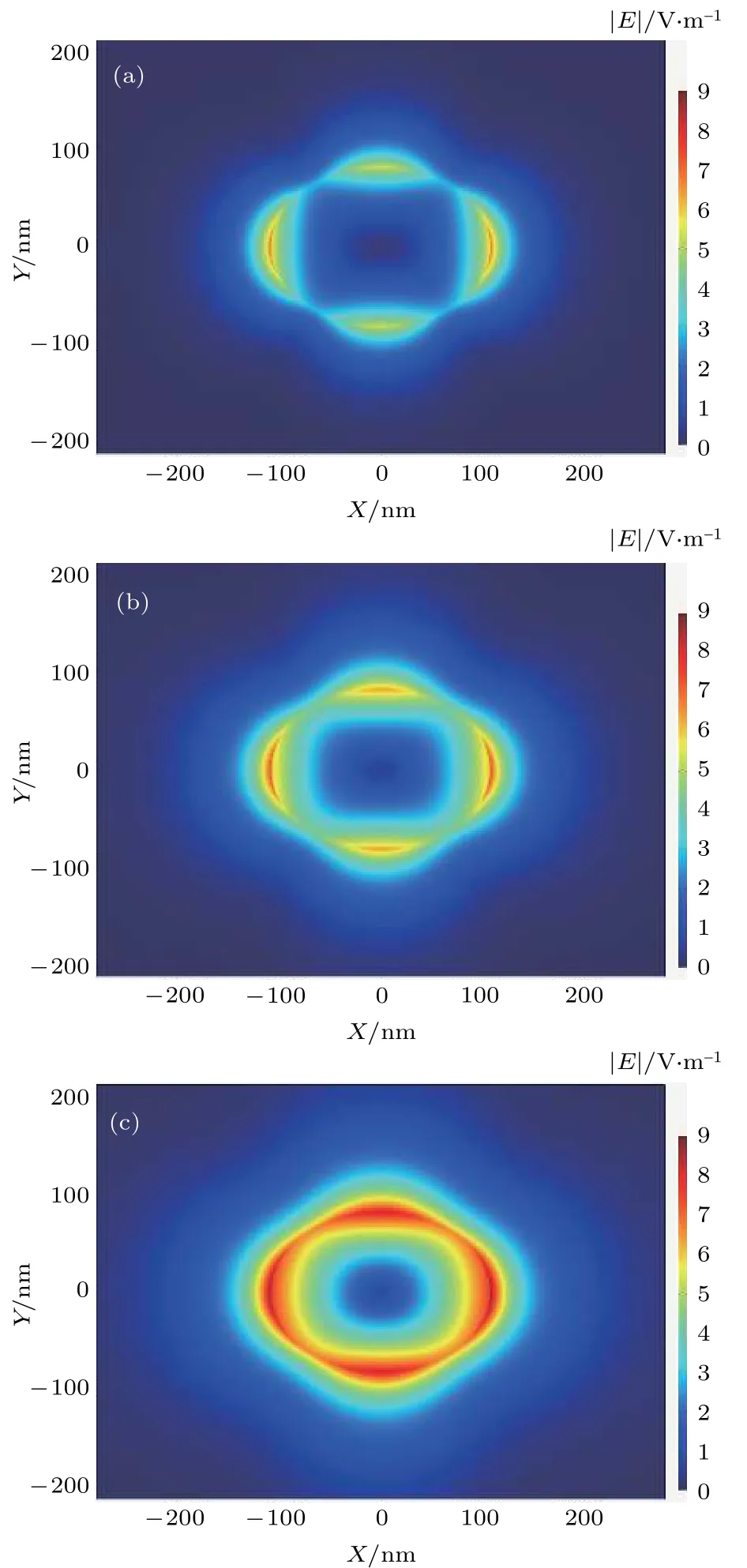
图10 在 a = 110 nm, b = 80 nm 和 的情况下,费米能取不同值时 Mode 5的电场强度 分布图(a) ; (b) ; (c)Fig. 10. The distribution of the electric field intensity of the Mode 5 with different values of Fermi energy when a = 110 nm, b = 80 nm, : (a) ;(b) ; (c) .

图11 在 和 b = 100 nm 的条件下, 当 a = 100 和 140 nm 时, Mode 5 的有效折射率实部 (a)和传播长度 (b) 随波长变化的曲线图Fig. 11. When a = 100 and 140 nm, the real part of the effective refractive index (a) , propagation length (b) as a function of wavelength at and b = 100 nm.

图12 在 b = 100 nm 和 的条件下, 当 a = 100 和 140 nm 时, Mode 5 的有效折射率实部 (a)和传播长度 (b)随石墨烯费米能变化的曲线图Fig. 12. When a = 100 and 140 nm, the real part of the effective refractive index (a), propagation length (b) as a function of graphene Fermi energy at b = 100 nm and .
图9 (a)—图 9(c)分别给出了在 a = 110 nm,b = 80 nm 和情况下, 有效折射率实部、传播长度和品质因数FOM与费米能EF之间的依赖关系. 从图9中可以看出, 随着费米能的增大, 前5个模式的有效折射率的实部都单调减小, 其中 Mode 1, Mode 2 和 Mode 3 的有效折射率的实部下降较慢, 而 Mode 4 和 Mode 5的有效折射率的实部下降较快. 随着费米能的增大, Mode 1, Mode 2 与 Mode 3 的传播长度单调增加, Mode 4 和 Mode 5 的传播长度先增大随后减小. 随着费米能的增大, Mode 1, Mode 2 和 Mode 3的品质因数缓慢增大, Mode 4 和 Mode 5 的品质因数逐渐减小.
上述现象可以通过场分布来解释. 石墨烯的表面电导率可以通过改变费米能级的大小来改变, 因此波导模式的传输性能还可以通过石墨烯的费米能级来调节. 以 Mode 5 为例, 图 10 给出了,和情况下的电场强度分布对比图.从图中可以看出, 当时, 场被紧密地约束在石墨烯涂层附近, 场与石墨烯涂层之间的相互作用强, 此时波导对场的约束性非常强, 能量分布集中, 模式的传输损耗较大, 传播长度较小. 当涂层之间的相互作用变弱, 波导对场的束缚性变弱 , 传 输 损 耗 减 小 , 因 而 传 播 长 度 增 大 . 当之间的相互作用变强, 传输损耗增大, 因而传播长度减小.
4 结 论
本文设计了一种涂覆石墨烯的椭圆形电介质纳米线波导. 在椭圆柱坐标系中, 借助Mathieu函数, 通过分离变量法, 推导出色散方程, 并通过数值方法求解了这个色散方程. 研究了波导最低阶的5个模式的传输特性, 以及工作波长、半长轴、半短轴、费米能的变化对这5个模式的传输特性的影响, 并对各参数变化时, 各个模式的品质因数进行了对比, 选出了最优的模式. 结果表明: 工作波长从 4.3增大至 8.8时, 5 个模式的有效折射率的实部都减小, 基模与一阶模的传播长度增大, 二阶模的传播长度先增大后减小; 当半短轴一定, 半长轴从 95 nm 增大至 140 nm 时, 有效折射率的实部逐渐增大, 其中 Mode 3 变化极小, 除Mode 3的传播长度缓慢减小外其他模式的传播长度都增大; 当半长轴一定, 半短轴从60 nm增大至105 nm 时, 除 Mode 2 的有效折射率的实部与传播长度减小外, 其他模式的有效折射率的实部与传播长度都增大; 费米能从到变化时,前5个模式的有效折射率的实部都减小, 基模与一阶模的传播长度增大, 二阶模的传播长度先增大后减小. 分离变量法的计算结果与有限元法仿真的结果一致. 本文所研究的涂覆石墨烯的椭圆形电介质波导在中红外到太赫兹波的保偏传输方面具有应用前景.
