硒化镉纳米线在应力作用下的第一性原理研究

姜 豹，汪礼胜，曹功辉，陈凤翔

(武汉理工大学理学院, 武汉 430070)

1 引 言

半导体纳米线结构是研究在微纳尺度和纬度上材料的物理和化学性质的理想体系，其在光电探测器、太阳能电池、热电材料和场效应晶体管等方面具有十分广泛的应用前景。Ⅱ-Ⅵ族化合物半导体材料硒化镉CdSe具有独特的光电特性，被认为是制作纳米线的优异材料，因而引起人们广泛地关注。由于CdSe纳米线具有较大的比表面积，因此，具有更好的电学特性[1]，其在半导体沟道器件领域具有很大的应用潜力[2]。

CdSe是直接带隙半导体，其带隙约为1.74 eV[3-4]，载流子迁移率约为800 cm2·V-1·s-1。通过掺杂CdSe可以形成n型半导体和p型半导体[5]。然而，目前对CdSe纳米线载流子迁移率的研究还很少。为了提高纳米线结构的光电性能，可通过施加应力调控其能带结构，以实现增强载流子输运性能。2011年，Peng等[6]发现可以通过施加应变力有效地调节Si/Ge纳米线的能带结构，Yang等[7]发现不同尺寸的纳米线在受到应变作用时，其带隙的变化情况是不同的。因此，为了提高CdSe纳米线的电学性能，可以通过调控施加在纳米线上应力的大小[8]以及改变纳米线的尺寸，以改变CdSe纳米线的禁带宽度和载流子迁移率，最终实现对纳米线输运能力的调控。

本文基于密度泛函理论，通过对CdSe纳米线的能带结构、载流子的有效质量和迁移率在应力调控和尺寸变化下的计算和分析，实现纳米线的性能优化，为实验上制得高性能CdSe纳米线提供理论指导。

2 计算模型与参数

CdSe有三种结构[9]，分别为立方闪锌矿结构、六角纤锌矿结构和立方岩盐矿结构，其中闪锌矿结构不稳定，适度加热会转变为纤锌矿结构，转变温度约为130 ℃，而岩盐矿结构仅能在高压下形成。图1给出了CdSe两种常见的结构：立方闪锌矿结构和六角纤锌矿结构。

图1 CdSe两种常见的结构示意图Fig.1 Two common structure diagrams of CdSe

本文采用六角纤锌矿结构的CdSe并沿[0001]方向[10]构建了一维纳米线模型，其中纤锌矿CdSe的晶格常数为a=b=0.4299 nm，c=0.701 nm。为了研究CdSe纳米线的尺寸对载流子输运性能的影响，建立了三种不同横向尺寸(直径分别为1.2 nm、1.6 nm和2.4 nm)的纳米线，分别标记为W-1、W-2和W-3，如图2所示。CdSe纳米线结构的优化与计算使用的是基于密度泛函理论[11]的ATK软件包，采用广义梯度近似(GGA)，交换关联泛函和优化方式则分别选取的是PBE和L-BFGS。体系截断能设置为75 Ha，温度取300 K，整体优化使其每个原子受力小于等于0.005 eV/Å，晶胞受力小于0.01 GPa。其中布里渊区积分所用的K空间取样采用Monkhorst-Pack方法，K点网格取1×1×21，得到了较好的收敛结果。为了减小由于周期性边界条件而引起相邻纳米线之间的相互作用，在纳米线的a和b方向上施加了1.5 nm的真空层[12]。

图2 CdSe纳米线的横截面示意图Fig.2 Cross-section diagrams of CdSe nanowires

为了研究施加应力对CdSe纳米线输运能力的调控，定义应变[13]ε=(L-L0)/L0，L0和L分别表示施加应变力前后的晶格常数。计算中应变ε从-10%增加到10%，增量为2%，其中ε<0是压缩应变，ε>0是拉伸应变。根据晶体的能带结构，可以利用式(1)计算出导带底(CBM)和价带顶(VBM)的载流子迁移率[14]。

(1)

3 结果与讨论

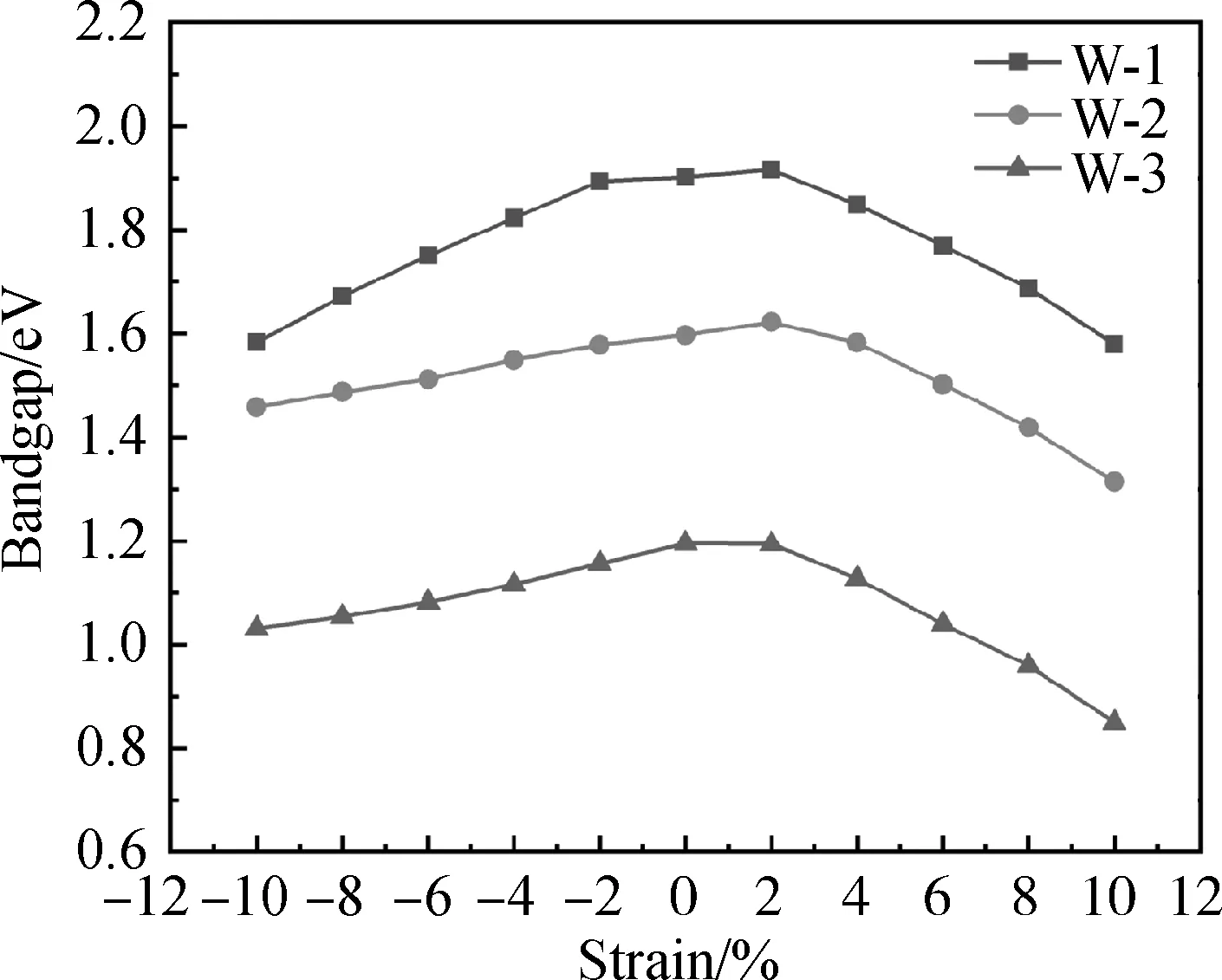
图3 三种横向尺寸CdSe纳米线在应力调控下的带隙宽度Fig.3 Bandgap of CdSe nanowires with three transverse dimensions under strain

图3给出了三种横向尺寸的CdSe纳米线在受到不同应力作用时带隙宽度的变化。从图中可以看出，加应力后直径更大的CdSe纳米线所呈现的带隙宽度更小，这是由于量子限制效应的影响。对于直径较小的纳米线W-1，压缩应力与拉伸应力均会对带隙宽度产生较大的影响；对于直径较大的纳米线W-2和W-3，压缩应力对CdSe纳米线带隙宽度的影响较小，而拉伸应力所产生的影响较大，在拉伸应变大于2%时，带隙宽度减少得非常明显。

图4给出了W-1纳米线几个典型应力作用下的能带图。从能带图上可以看出，导带底和价带顶始终都出现在Γ点处，不受应力的影响。这说明无论施加何种应力，CdSe纳米线会一直保持着直接带隙半导体的属性。在不施加应力的情况下，完全弛豫W-1纳米线得到的带隙宽度为1.901 eV，在拉伸应变为2%时，完全弛豫后纳米线带隙宽度增加到最大值为1.916 eV；在拉伸应变增加到10%的过程中，带隙宽度逐渐减小至1.579 eV。与此类似，在压缩应变-10%时，带隙减小至1.583 eV。从能带图中还可以发现，无论施加何种应变，价带顶的位置几乎没有变化。而导带底的位置在压缩或拉伸应变的作用下，都会向费米能级偏移，因此会使得CdSe纳米线的带隙减小。此外，计算结果还显示，W-2纳米线的带隙宽度最大值出现在施加应力的应变为2%时，带隙大小为1.622 eV；W-3纳米线的带隙宽度最大值出现在未施加应力时，带隙大小为1.195 eV。

对于不同尺寸的CdSe纳米线，可以发现所施加的拉伸应变对带隙宽度的影响大于压缩应变的影响。W-1、W-2和W-3纳米线施加应力的拉伸应变为10%时，带隙相比于未施加应力时分别减小了16.9%、17.7%和28.8%，而施加应力的压缩应变为-10%时，它们的带隙分别减小了16.7%、8.7%和13.7%。根据图4所示的W-1纳米线的能带图还可以看出，随着拉伸应变和压缩应变的增加，导带底的位置在逐渐下降，但是导带底的能带形状并未发生改变。在应变从2%增加到4%的过程中，价带顶的能带发生了迁移，由2%应变下的实线能带变成了4%应变下的虚线能带。正是由于能带迁移的出现，使得价带顶的空穴性质发生了变化。

图5(a)和(b)分别给出了三种横向尺寸CdSe纳米线导带底电子有效质量和价带顶空穴有效质量随应变的变化。从图中可以看出，随着拉伸应变的增加，所有CdSe纳米线导带底电子有效质量都在逐渐减少。W-1纳米线电子有效质量最大值出现在未施加应力时，而W-2和W-3纳米线电子有效质量最大值出现在压缩应变为-6%时，它们相应的最大有效质量分别为0.312、0.269和0.178。从整体来看，随着拉伸和压缩应变的增加，价带顶空穴有效质量会逐渐降低。对于W-1纳米线，空穴有效质量从-10%压缩应变时的-0.456缓慢增加到2%拉伸应变时的-0.377。然而当施加应力的应变为4%时，空穴有效质量急剧减少到-1.204，继续增加应力，空穴有效质量逐渐缓慢减小。W-2和W-3纳米线同样也有空穴有效质量急剧减小的现象。W-2纳米线的拉伸应变从2%增加到4%时，空穴有效质量由-0.31下降到-1.361；W-3纳米线的拉伸应变从0%增加到2%时，空穴有效质量由-0.251下降到-1.302。价带顶空穴有效质量明显变化的原因是在对CdSe纳米线施加应力时，价带顶能带发生偏移的结果。

图4 不同应变下的W-1纳米线的能带图Fig.4 The band structure of W-1 nanowire under various strain

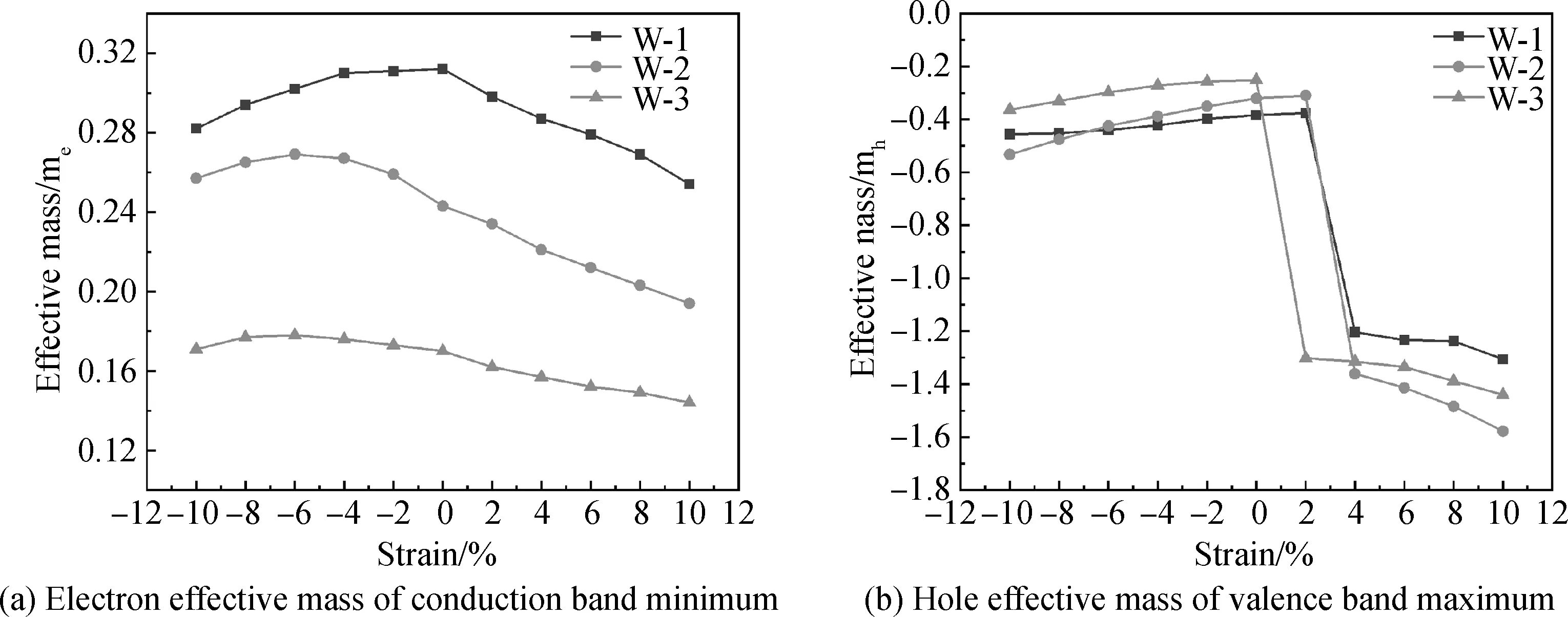
图5 载流子有效质量随应变的变化曲线Fig.5 The evolution of carriers effective mass with strain

为了研究CdSe纳米线的输运特性，分别计算出每种纳米线的弹性模量C1D，并且根据公式(1)计算出导带底电子迁移率以及价带顶空穴迁移率，如图6所示。弹性模量可视为衡量材料产生弹性变形难易程度的指标。计算结果发现，纳米线的直径越小(如W-1)，其弹性模量越小，如图6(a)所示，即直径越小的纳米线越容易在外力的作用下发生形变。对于W-1纳米线，应变从-10%增加到10%的过程中，弹性模量在逐渐减小。值得注意的是，对于W-2和W-3纳米线，随着应变从压缩应变到拉伸应变的变化，弹性模量存在先增加后减少的过程。

图6(b)是W-1纳米线的载流子迁移率随应变的变化曲线。由图可以看出，当应变从-10%增加到10%的过程中，载流子迁移率均在减少。其中，由于价带顶的改变导致空穴有效质量的急剧减少，导致纳米线的空穴迁移率在对应的应变处也出现了急剧的下降，空穴迁移率由1765 cm2·V-1·s-1下降到927 cm2·V-1·s-1。对比W-1、W-2和W-3纳米线载流子迁移率曲线图6(b)、(c)和(d)，可以发现，纳米线尺寸越大，则相应的载流子迁移率越低。在施加压缩应变-10%时，W-1、W-2和W-3纳米线的电子迁移率分别约为2890 cm2·V-1·s-1、1084 cm2·V-1·s-1和323 cm2·V-1·s-1。对所有的CdSe纳米线，随着施加应变的增加，导带底电子迁移率在不断减少，而价带顶空穴迁移率随应变的变化较为复杂。W-1纳米线在施加-10%～10%的应变过程中，空穴迁移率逐渐减少，其中应变在2%～4%时，空穴迁移率下降很快；W-2纳米线在施加-10%～-2%的压缩应变过程中，空穴迁移率逐渐增加，而在施加-2%～10%的应变时，其空穴迁移率逐渐减小，其中急剧减少发生在应变为2%～4%；W-3纳米线在施加-10%～-6%的压缩应变过程中，空穴迁移率逐渐增加，而在施加-6%～10%的应变时，其空穴迁移率逐渐减小，应变在0%～2%时，空穴迁移率出现急剧减小。W-1、W-2和W-3纳米线在施加的压缩应变分别为-10%、-2%和-6%时，空穴迁移率有最大值，分别为2273 cm2·V-1·s-1、896 cm2·V-1·s-1和227 cm2·V-1·s-1。由以上分析可知，横向尺寸较小的CdSe纳米线(如W-1)在施加合适的压缩应变时，可以有效地提高CdSe纳米线的电子迁移率和空穴迁移率。然而对于CdSe纳米线横向尺寸(直径)小于1.2 nm时，其横截面仅为一个六元环的结构，这样的结构不稳定，因此纳米线的直径应不小于1.2 nm。

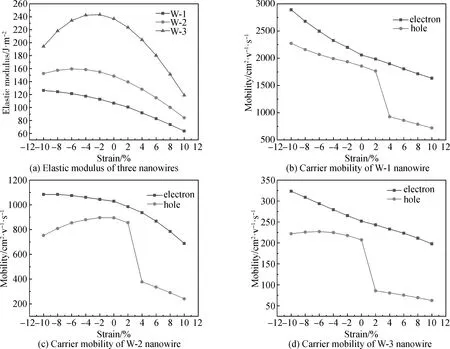
图6 W-1、W-2和W-3纳米线的弹性模量和载流子迁移率随应变的变化关系Fig.6 The evolution of elastic modulus and carrier mobility with strain in W-1, W-2 and W-3 nanowires

4 结 论

本文基于密度泛函理论的第一性原理计算分析了应力和尺寸的变化对CdSe纳米线的能带结构和载流子迁移率的影响。计算结果表明，无论是施加应变还是改变纳米线尺寸，CdSe纳米线均表现为直接带隙。随着压缩应变(0%～-10%)和拉伸应变(2%～10%)的增加，CdSe纳米线的带隙逐渐减小，由于量子限制效应，尺寸小的CdSe纳米线具有更大的带隙。导带底电子迁移率随着应变从压缩应变到拉伸应变的变化(-10%～10%)而逐渐减少，而价带顶空穴迁移率在施加的应变为4%～10%时也在缓慢减少。W-1、W-2和W-3纳米线在施加压缩应变为-10%时，电子迁移率的最大值分别约为2890 cm2·V-1·s-1、1084 cm2·V-1·s-1和323 cm2·V-1·s-1。而在施加的压缩应变分别为-10%、-2%和-6%时，它们的空穴迁移率有最大值，分别为2273 cm2·V-1·s-1、896 cm2·V-1·s-1和227 cm2·V-1·s-1。因此，横向尺寸较小(如1.2 nm直径)的CdSe纳米线施加以合适的压应力，可以有效地改善纳米线的能带结构和提高其电子和空穴迁移率，表明一维CdSe纳米线拥有作为制备新型微纳米电子器件沟道材料的潜力。