基于概念漂移检测的数据流集成分类

张宝菊，陈一迪，薛 磊

（天津师范大学 天津市无线移动通信与无线电能传输重点实验室，天津 300387）

现实生活中不断产生着大量数据.从数据分布角度来看，静态数据的分布相对稳定，而数据流是动态的，其包含的概念可能随时间变化而不断改变，即发生概念漂移.概念漂移不仅要求数据流上的学习算法具有较高的分类精度，而且还要能够适应动态变化的环境并做出正确的决策.目前，相关领域的学者已提出许多有效的学习算法来检测数据流的概念漂移[1-12].文献[1]基于概念相似性的错误方差提出了DDM（Drift detection method）方法，该方法根据伯努利数据分布设定阈值来区分概念漂移和噪声漂移.文献[2]提出的基于信息熵的概念漂移检测方法通过比较2个相邻窗口的数据分布差异来判断概念漂移及重复概念.文献[3]利用约束惩罚回归组合器来追踪挖掘概念漂移.文献[4]首次将集成分类技术引入到数据流分类中，并提出了SEA算法.文献[5]针对集成分类器训练时间过长的问题，提出了一个在线的集成分类器模型.本文着重分析概念漂移对分类器的影响，在一定的概率下检测概念漂移，并将其应用于基于Choquet模糊积分[13]的集成学习算法，从而构建一个集成分类器，实现漂移检测的同时及时更新分类器模型.

1 概念漂移的并行检测机制

1.1 基于错误率的检测方法

错误率是衡量概念漂移算法的常用指标，当发生漂移时，分类模型将不再适合当前的概念，错误率就会上升.将数据集划分为数据块的形式，每个数据块包含N个样本，目标函数f在数据块D上的错误率记作errorD（E），其中D满足分布Φ.若前一个数据块的错误率是errori（E），则当前数据块上的错误率是errori+1（E），当errori+1（E）∈（errori（E）-σzα，errori（E）+σzα）时，在1-α的置信度下，当前数据块不会发生概念漂移，否则认为当前数据已经出现异常.其中：zα是由置信度α和标准正态分布决定的常量，σ≈

1.2 基于漂移度的检测方法

为了比较当前数据块和前一数据块之间的差异，本研究采纳欧氏距离定义漂移度的概念.对于当前数据块中的每个样本（实例）xi，计算其与前一数据块中所有样本的欧氏距离，并比较它们的值，将距离最小值的样本定义为最近邻样本，欧式距离计算公式为

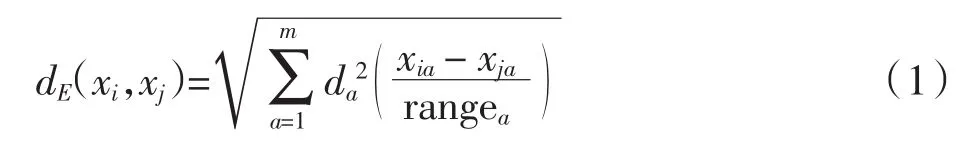
其中：xi是当前数据块中的实例；xj是前一个数据块中的实例；m是xi、xj的属性数.对于数值属性a，rangea是该属性数值中最大值和最小值的差，此处对其值的范围进行了归一化处理.

比较xi与其最近邻实例的类别标签，如果它们具有相同的类别， 则令 dis（i）=0， 否则 dis（i）=1.漂移度DE的计算公式为

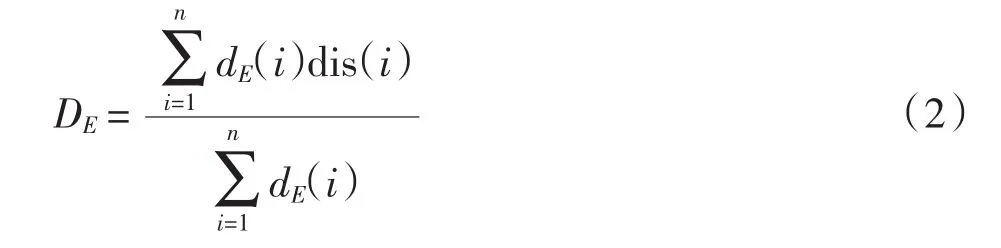
其中dE（i）为dE（xi，xj）的最小值.若漂移度DE的值增加，则认为发生了概念漂移.

1.3 概念漂移的并行检测

基于错误率和漂移度，本文提出概念漂移的并行检测机制.首先使用学习算法训练模型获得每个数据块的分类错误率，然后比较预测错误率，若其超出单侧置信区间，再计算基于欧氏距离的概念漂移度，若漂移度上升，表明数据分布很可能发生了变化，认为发生了概念漂移.其实现过程如下：

输入 数据块 D1，D2，…，Di，Di+1，…； 每个数据块包含的样本数为N.

输出分类错误率errori；漂移度DE（i）；预测结果.

过程

①按照数据流到达的顺序将其分块，数据块包含的样本数均为N.

②初始化errori=0，DE（i）=0.

③对每一个数据块Di，使用贝叶斯分类算法进行分类，返回分类错误率.若

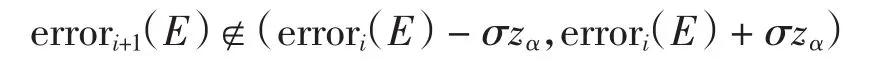
则计算基于欧氏距离的漂移度DE（Di+1）和DE（Di），若DE（Di+1）＞DE（Di），则判定发生概念漂移.

2 基于模糊积分的集成系统

2.1 模糊测度μ和Choquet积分

本文利用Choquet模糊积分[14]构建集成分类器.

定义1设X为非空集合，F（X）为其子集构成的集合，称μ：F→[0，∞）为定义在F（X）上的模糊测度，若

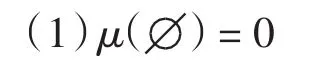
（2）对任意 X1、 X2∈F（X）， 若 X1⊂X2， 则 μ（X1）≤μ（X2）， 即具有单调性.

在分类器学习领域，通常用μ表征各分类器的重要程度.μ的值越高，其分类结果准确率越高，这里直接将μ值视为各分类器的预测准确率.

定义2对于一个有限集合X={x1，x2，…，xn}，令μ为定义在X上的一个模糊测度，h是定义在X上的实值可测函数，则h关于μ的Choquet模糊积分为

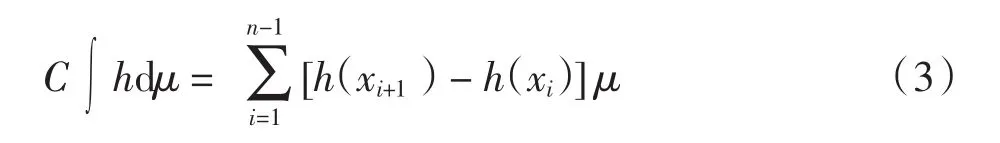
其中： 0≤h（x1）≤…≤h（xn）≤1， C 为常数.

2.2 基于Choquet模糊积分的集成分类系统

以模糊测度μ和基分类器的输出作为Choquet积分的输入，构建集成分类系统.设L个分类器为E1，E2，…，EL，通过对样本x的学习，每个分类器得到一个m维向量.L个分类器的向量构成矩阵

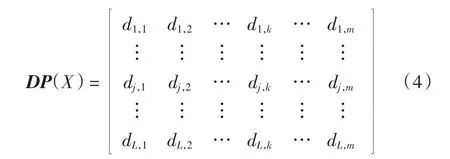
其中：第j行为第j个分类器的m维向量；dj，k表示第j个分类器判断样本为第k类的可能性.

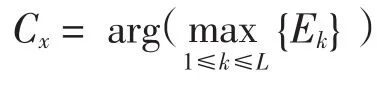
基于Choquet积分的分类器集成过程如图1所示.

2.3 用于概念漂移的模糊积分集成系统

对每一数据块进行独立学习，得到每个分类器的分类性能，确定μi，作为Choquet积分的因子.根据式（3）和式（4）计算当前样本属于每个类别的可能性，并根据最大隶属原则选择预测类别作为最终的分类输出.

根据并行检测机制对概念漂移进行检测，若检测到概念漂移，则利用模糊测度重新计算Choquet积分，选择具有最大值的类别作为最后的分类输出结果，动态更新集成分类系统，以适应新的数据流环境.

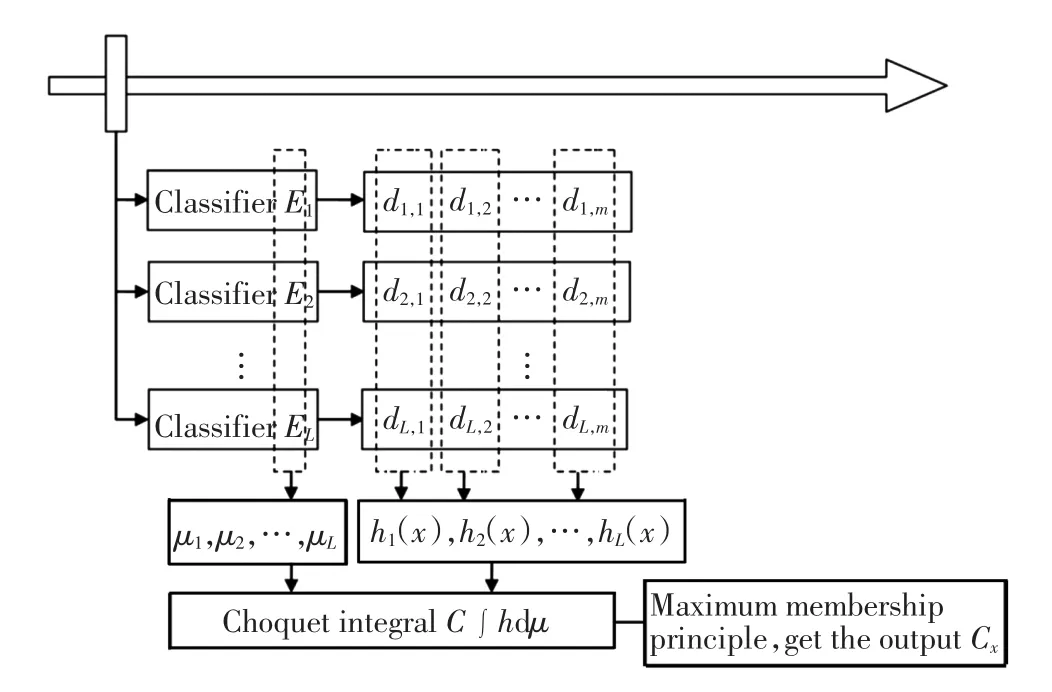
图1 基于Choquet积分的集成系统框架Fig.1 Integrated system framework based on Choquet integral

3 实验

3.1 数据集

（1）UCI数据库：本文选择UCI中的Ionosphere、Iris、Hypothyroid等3个数据集.数据集的实例数NI，属性数NA和类别数NC见表1.

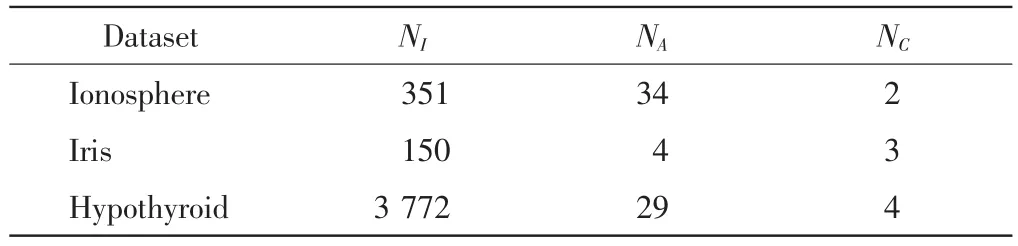
表1 UCI库的数据集描述Tab.1 Dataset description of UCI library

（2）SEA 数据集：SEA 数据集的结构为（f1，f2，f3，C），其中：f1、f2为条件属性，f3为不相关属性，C为包含2个类别标签的类别属性.当f1+f2≤θ时，实例属于类1，否则属于类2.给定阈值θ，当阈值分别为9、8、7和9.5时，可以形成4个不同的概念.该数据集由MOA生成，它是一款开源数据流挖掘软件，可生成具有概念漂移的数据.实验中随机生成104个实例，包含4个概念和3个概念漂移，噪声率为10%.

（4）瑞典电网数据集：为了评估算法在实际应用中的性能，选取了瑞典电网数据集进行实验.该数据集为真实数据集，包含2 190个实例，12个条件属性，按照时间分为2种类别.该数据集可用于检测电力消费中的概念漂移.

3.2 实验分析

实验1为验证并行检测机制的有效性，在SEA数据集上进行实验，使用误检率（False alarms）、漏检率（Missing）以及检测时延（Delay）3个指标对概念漂移检测方法进行性能分析，包含3次漂移，噪声率为10%，数据块大小为100.进行了10轮实验取平均值，结果见表2.

表2 SEA数据集上的概念漂移检测性能比较Tab.2 Performance comparison of concept drift detection on SEA datasets

由表2数据可见，本文的并行检测机制的误检率最低，时延最小，说明概念漂移的并行检测机制较单一检测更高效，结果更可靠.

实验2将本文的集成分类器与常见的经典集成算法（Vote、Stacking、Bagging）进行分类精度比较，实验在UCI库的3个数据集上分别进行，为保证实验的准确性，均采用十折交叉验证的方法，得到平均水平下的集成分类器的性能表现.实验结果见表3.

表3 模糊积分集成分类器与其他集成分类器的精度Tab.3 Accuracies of fuzzy integral ensemble classifier and other ensemble classifiers %

由表3数据可见，本文基于Choquet积分的集成分类器在3个数据集上均有较好的性能，仅在Ionosphere上略差于Stacking算法，总之，实验说明本文的集成分类器是有效的.

实验3为了测试本文的用于概念漂移的模糊积分集成系统的性能，选择MOA平台上常用的Naive Bayes、OzaBag和AWE算法作为对比算法.实验结合Weka和Matlab平台进行.

首先，在数据集SEA上进行实验，按数据到达的先后顺序进行分块处理，输入集成系统进行检测，实验结果见图2.

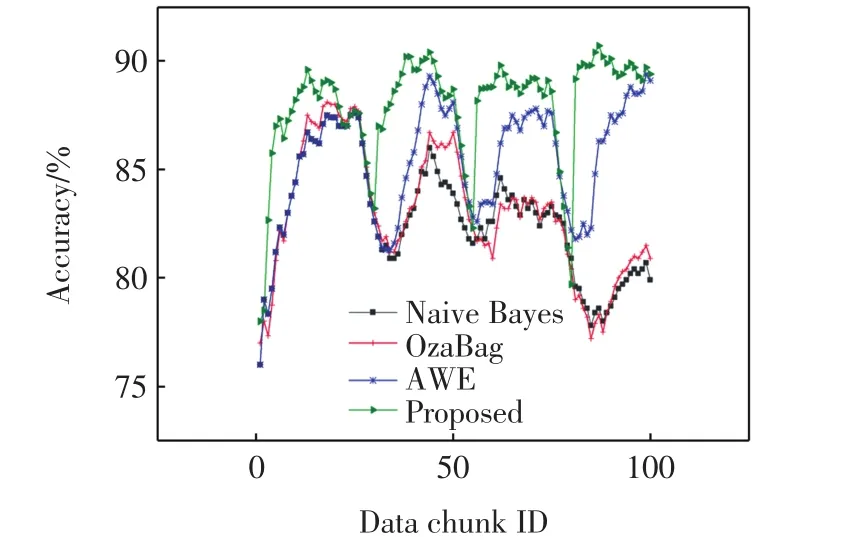
图2 SEA数据集的预测精度Fig.2 Predicted accuracies of the SEA dataset

由图2可知，在系统运行过程中，几种算法均出现 3 处（数据块范围为 20～30、45～55、70～80）较为明显的精度低点，这是受到概念漂移的影响，本文的集成系统能很快识别出概念分布的变化并进行更新，从而使精度迅速提升.在数据平稳阶段（5～20、30～45、55～70、80～100）， 本文算法的分类精度最高.

其次，将超平面数据集进行分块处理，数据集包含6×104个、噪声率为10%的实例，每104个实例发生一次漂移.实验结果见图3.

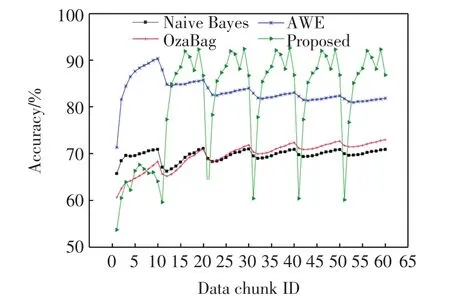
图3 超平面数据集的预测精度Fig.3 Predicted accuracies of the hyperplane dataset

由图3可以看出，在5次概念漂移发生的位置，4种分类算法的准确率均迅速下降.在无概念漂移发生时，本文算法具有更高的精度.在发生概念漂移的瞬间，本文算法的精度立即降到最低，而后又在短时间内迅速进入平稳阶段，这说明本文算法对概念漂移十分敏感.而其他3种算法在概念漂移发生时，其精度曲线起伏不明显.因此，本文模型更适合于对含有概念漂移的数据流进行分类处理.

最后，在瑞典电网数据集上进行实验，实验结果见图4.

图4 瑞典电网数据集的预测精度Fig.4 Predicted accuracies of the Swedish grid dataset

由图4可看出，本文模型与其他集成模型在某些数据块上均出现了精度降低的现象，这是概念漂移造成的.但本文模型一旦检测到概念漂移就会自适应调整，从而精度又迅速回升，而其他算法的精度起伏不明显，且其精度均低于本文模型，这说明本文模型更适用于真实数据流的概念漂移检测及分类集成.

实验4将本文算法与对比算法在各数据集上的整体分类精度进行比较，结果见表4.

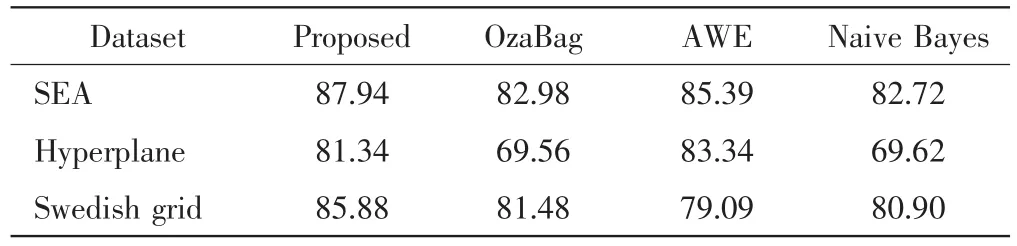
表4 实验数据集分类精度的比较Tab.4 Comparison of classification accuracy of experimental datasets %

由表4可见，本文算法与其他3种算法比较，除在超平面数据集上略差于AWE算法，在每个数据集上均具有更好的性能表现.

4 结语

本文提出一种概念漂移的并行检测机制，并利用Choquet模糊积分构建集成分类器.在不同数据集上进行实验，并与已有算法进行比较，结果表明该算法在分类精度和概念漂移检测方面均具有良好的性能，且对人工模拟数据流和真实数据流均具有较强的适应性和表现.