基于第三类Chebyshev节点组的Hermite插值
2019-03-25许贵桥王彩华
张 静,黄 蓉,许贵桥,王彩华
(天津师范大学 数学科学学院,天津 300387)
在平均框架下研究函数类的逼近问题是函数逼近论研究的热点.过去研究的大部分函数类是具有有限光滑性的函数空间,近些年许多学者开始研究具有无限光滑性乃至解析函数类上的问题,如文献[1-10].在讨论这些问题时,最常见的方法是多项式插值方法,而在以上研究中,误差分析都是针对光滑函数的,相应于解析函数的讨论大多仅针对Lagrange插值,如文献[11-13].本文讨论基于第三类Chebyshev节点组的Hermite插值对一种解析函数类的逼近问题,得到了相应量的强渐近阶或其值.
1 预备知识
设n为非负整数,将定义在[-1,1]上的n阶连续可导函数的全体记为Cn[-1,1],特别地,当n=0时,将[-1,1]上的连续函数的全体记为C[-1,1].
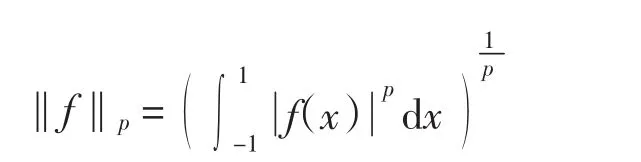
为函数 f在[-1,1]上的 Lp范数.
函数类An是[-1,1]上的解析函数的一个子集,定义如下:
An={f∈Cn[-1,1]:‖f(n)‖≤1,n=1,2,…}
n次第三类Chebyshev多项式[14]为
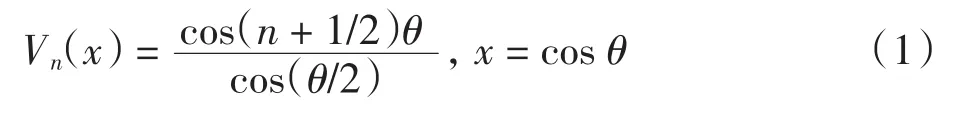
其中Vn(x)的零点为
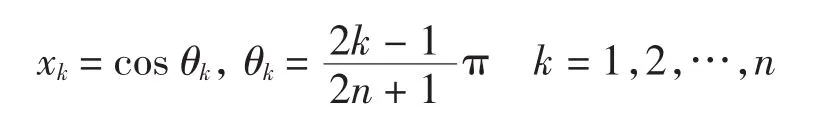
当θ=π时,
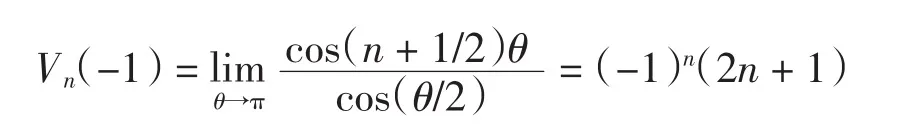
对任意 f∈C[-1,1],根据文献[15],计算可得基于上述节点组{xk}nk=1的Hermite插值多项式为
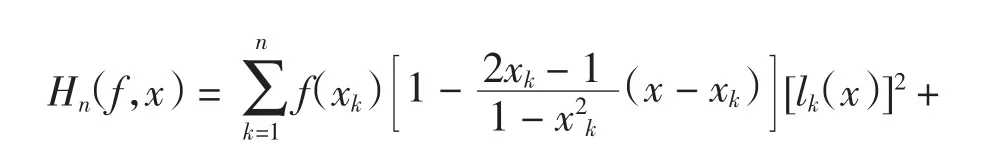
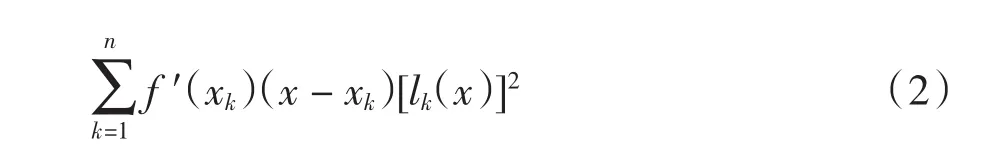
其中
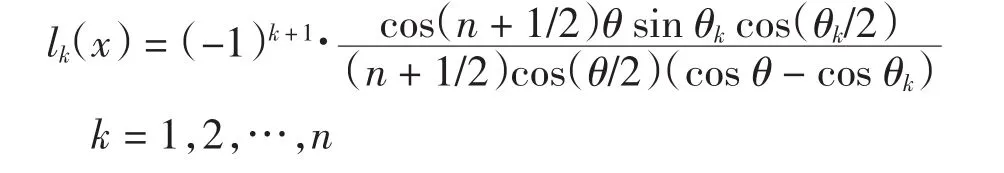
基函数lk(x)是n-1次多项式,因而插值函数Hn(f,x)是2n-1次多项式.
引理[15]若f∈A2n,Hn(f,x)由式(2)给出,则对任意 x∈[-1,1], 存在 ξ∈[-1,1], 使得
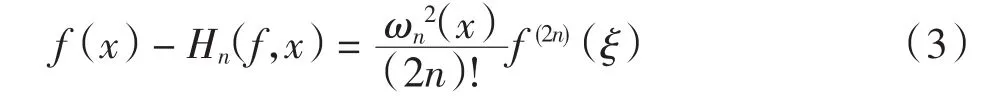
2 Hn在最大范数下的逼近误差
定理1设f∈A2n,Hn(f,x)由式(2)给出,则对任意 x∈[-1,1], 有
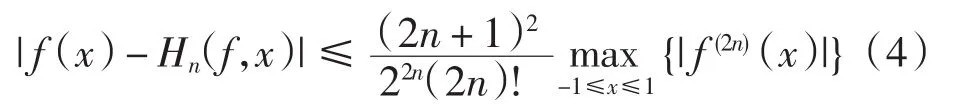
且式(4)的估计是精确的.
证明由文献[13]知
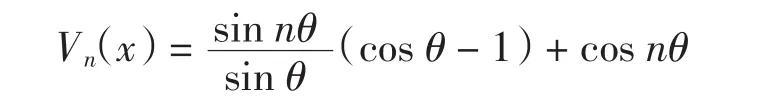
且Vn(x)=2nωn(x).由引理有
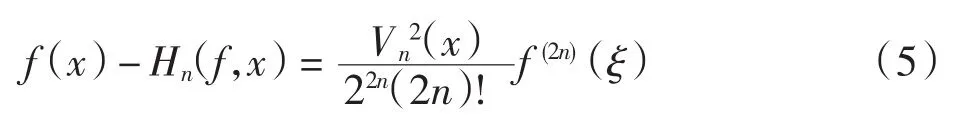
于是有
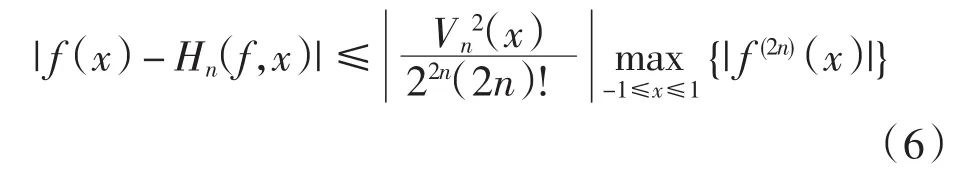
利用数学归纳法可证得
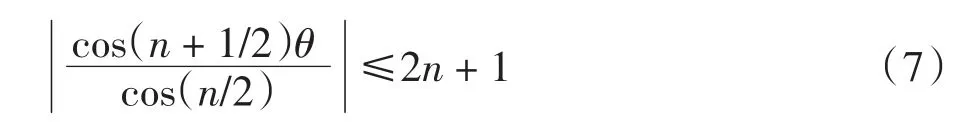
而当θ=π时,Vn(x)=(-1)n(2n+1),从而可知|Vn(x)|的最大值为2n+1,代入式(6)可得式(4)成立.
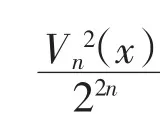
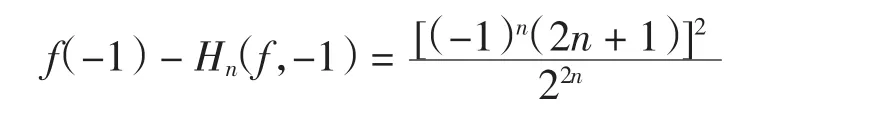
此时,式(4)中等号成立,从而此估计式是精确的,定理1得证.
在最大范数下,因为
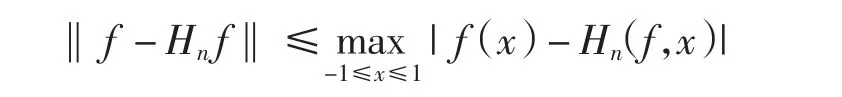
再由定理1可得如下推论成立.
推论设Hn(f,x)由式(2)给出,则有
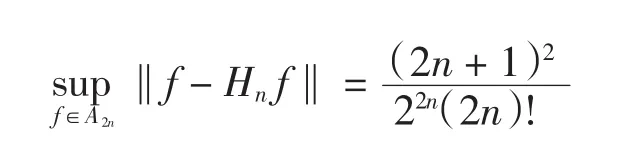
3 Hn在Lp范数下的逼近误差
定理2设Hn(f,x)由式(2)给出,则有
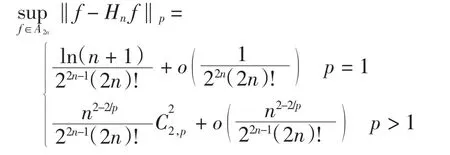
证明由式(6),当 f∈A2n时,有‖f(2n)‖≤1,且有
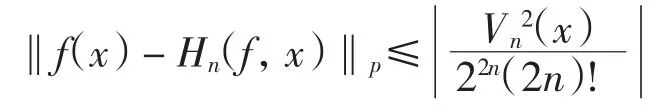
于是得
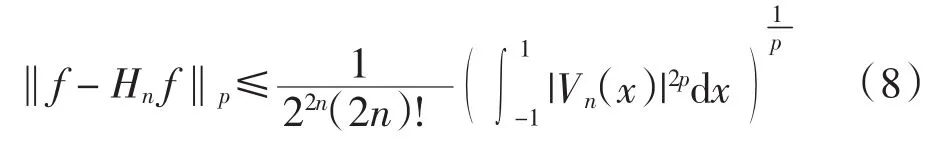
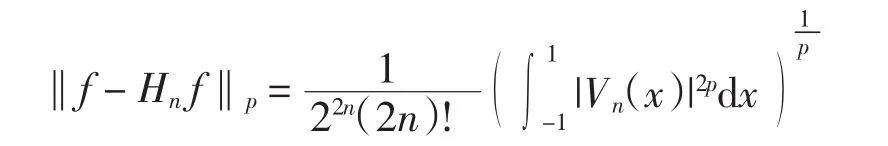
从而可知
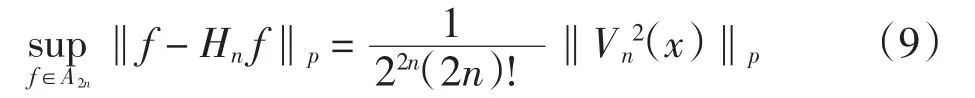
下面计算‖Vn2‖p.令

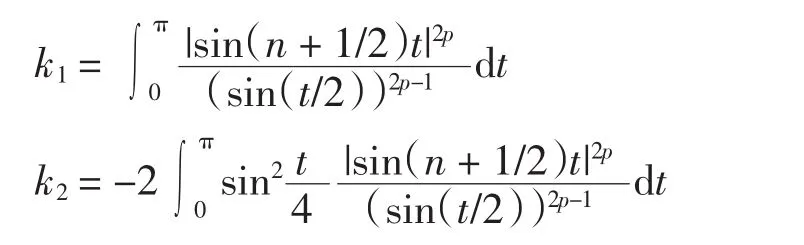
分2种情况讨论.
(1)当 p=1时.对于 k1有
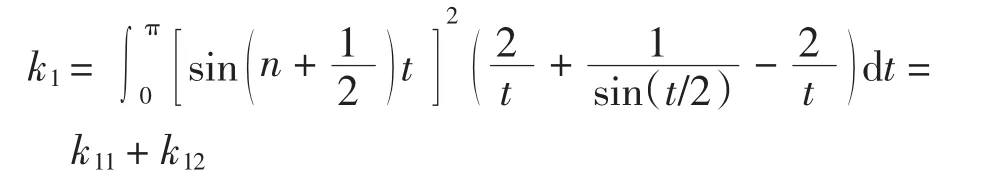
其中
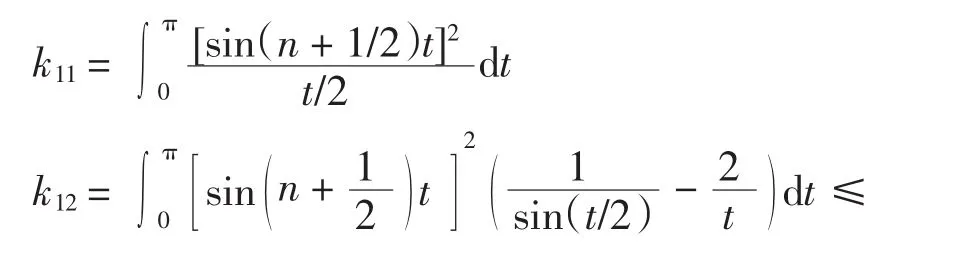
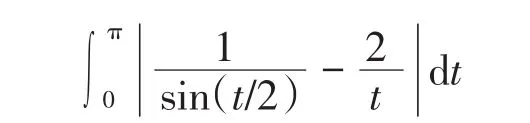
由等价无穷小知
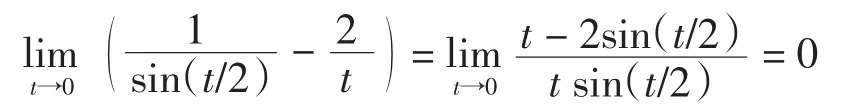
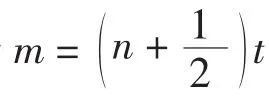
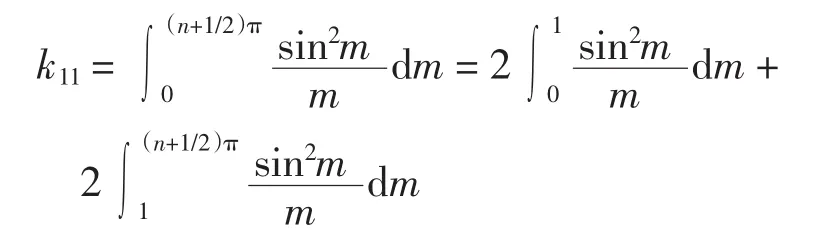
又因为|sin2m|≤|m|, 故有
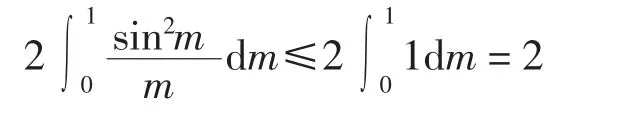
并且
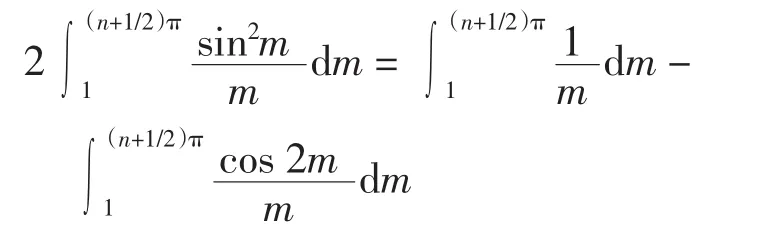
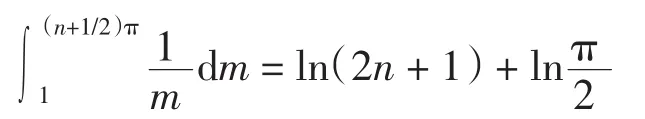
于是有
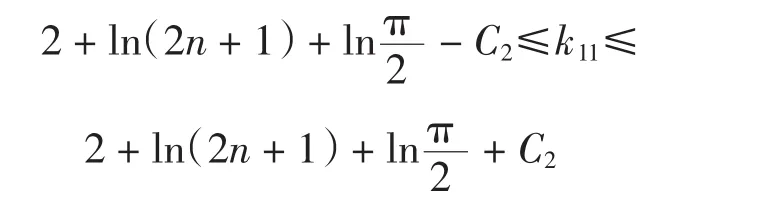
从而
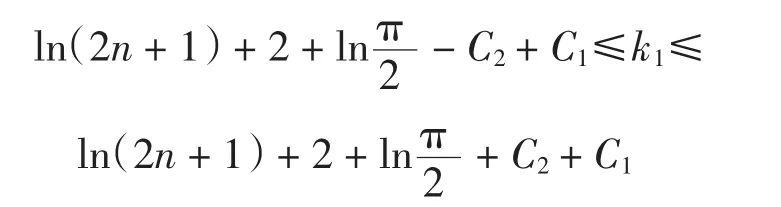
所以
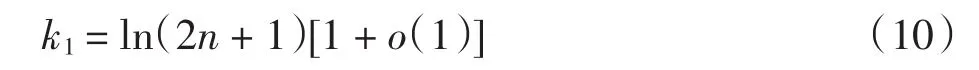
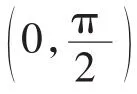
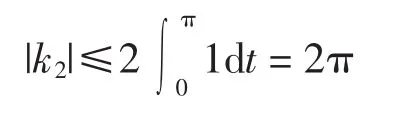
由上式和式(10)可得
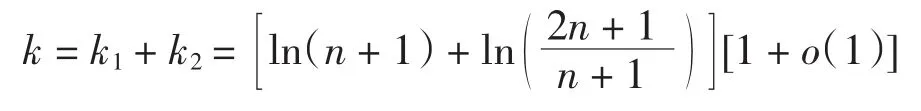
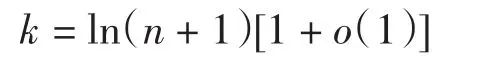
所以当p=1时,
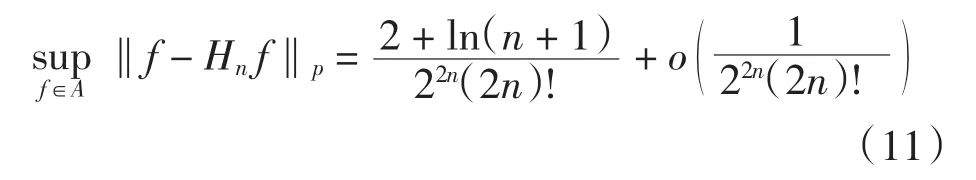
(2)当p>1时.对于k1有
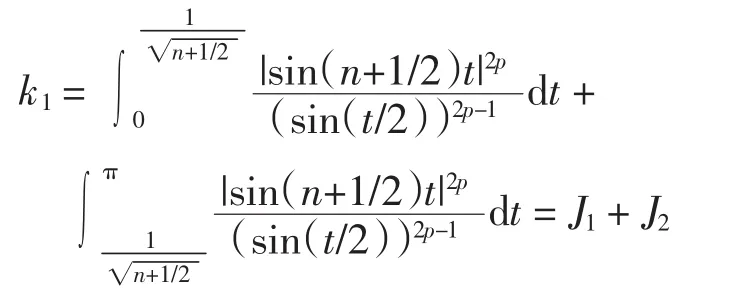
其中
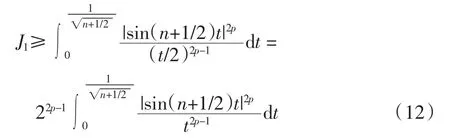
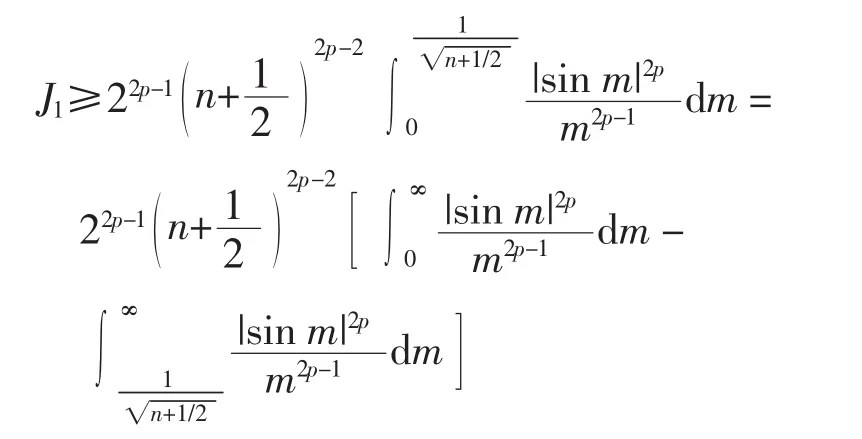
根据 C2,p的定义, 因为
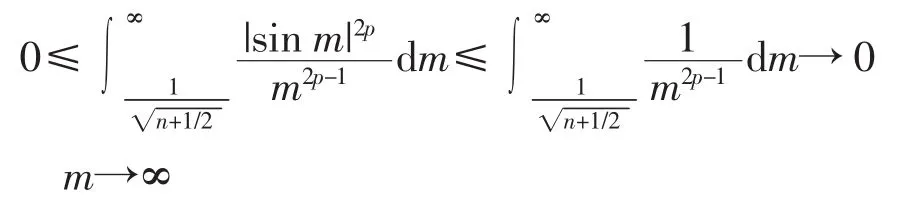
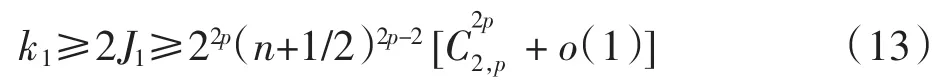
另一方面,
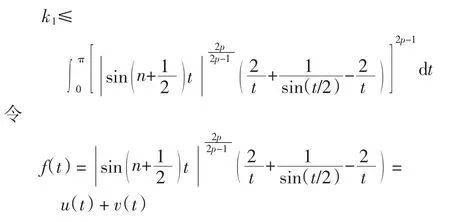
其中
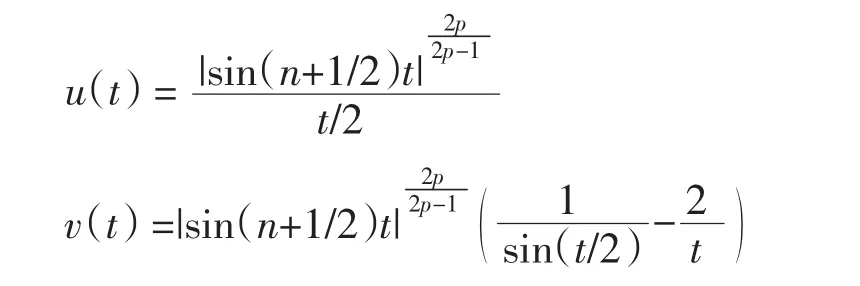
因为
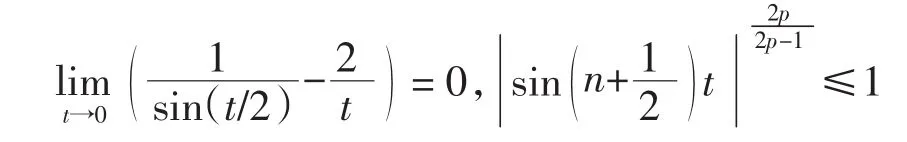
故存在常数 C4,使得|v(t)|≤C4, 所以有
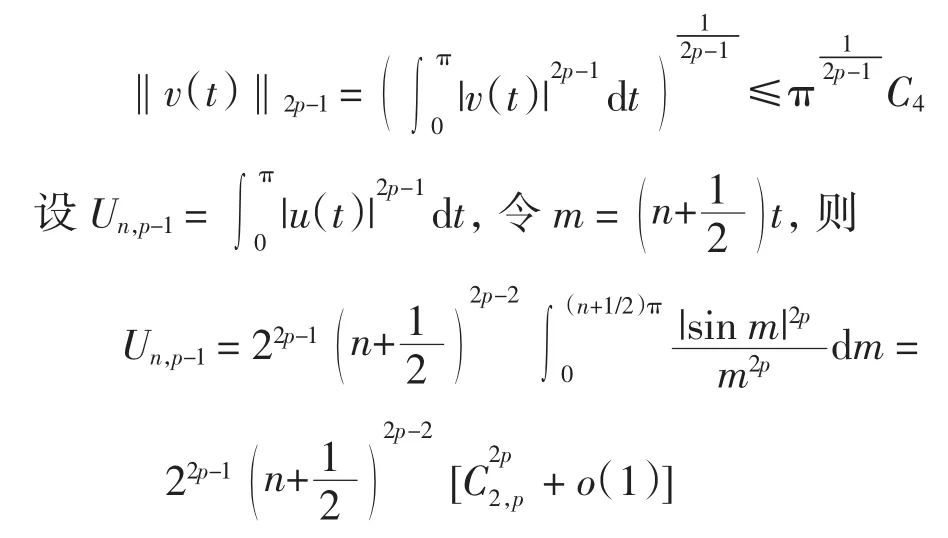
由范数性质可知
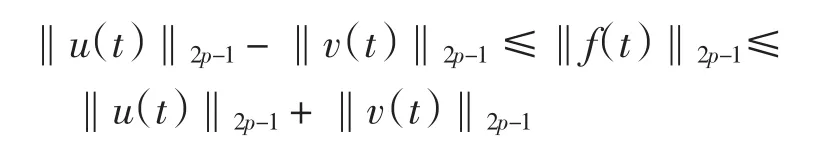
则
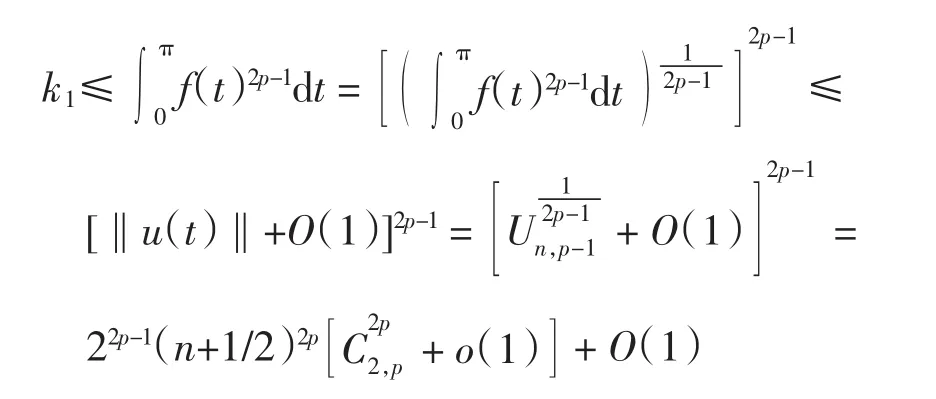
所以
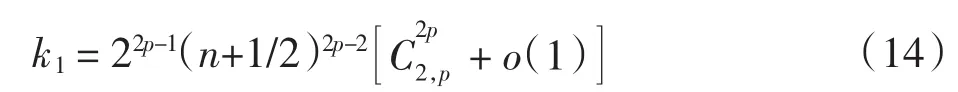
对于k2有
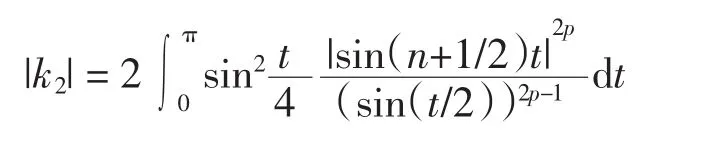
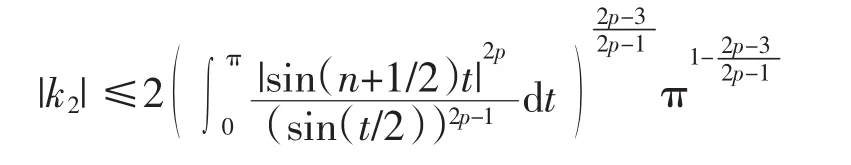
所以
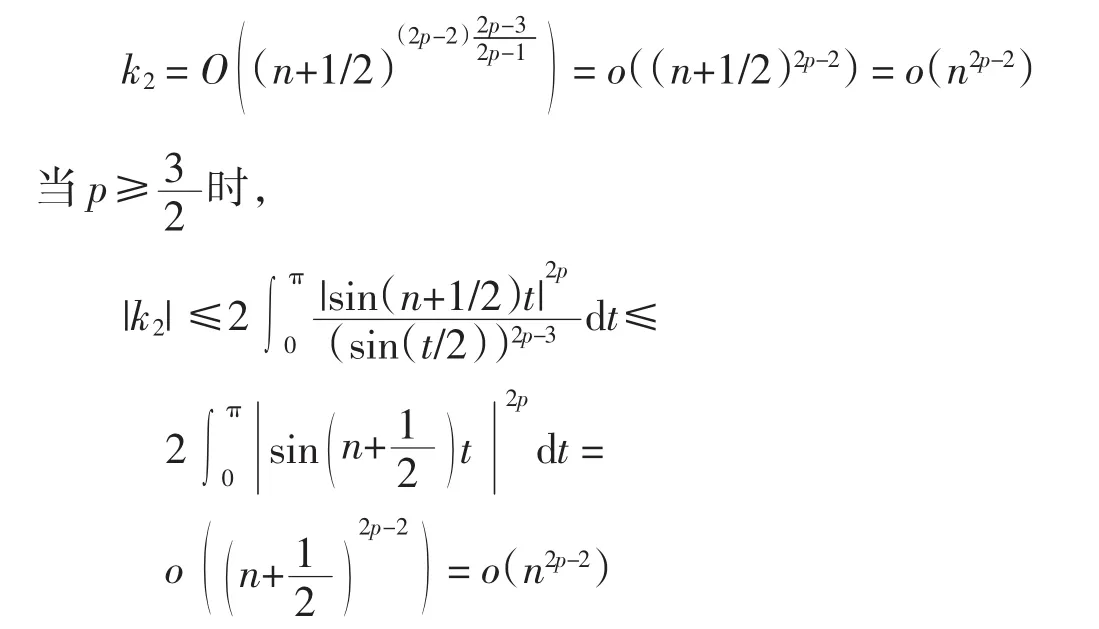
因此
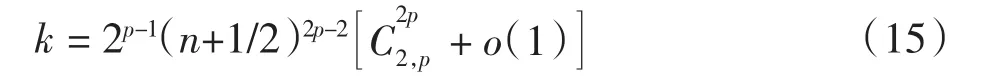
则p>1时,
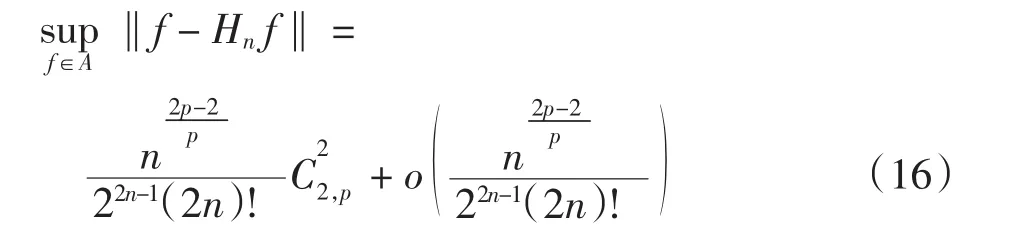
综上,由式(9)、式(11)和式(16),定理2得证.
4 数值实验
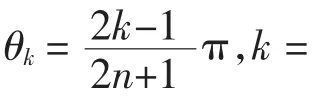
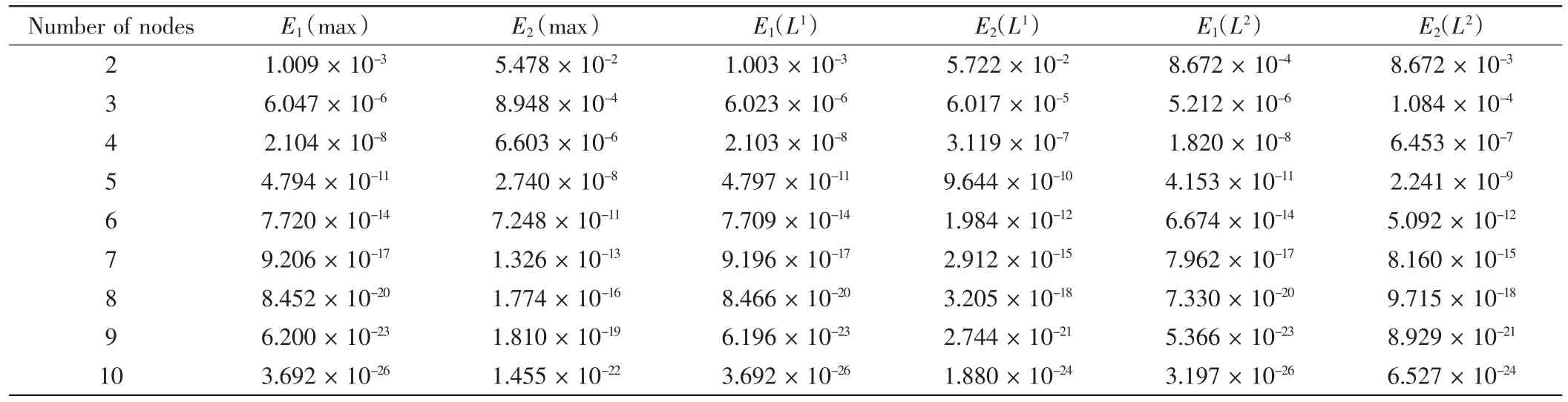
表1 例1的Hn在最大范数、L1范数和L2范数下的逼近误差Tab.1 Approximate errors of Hnunder maximum norm,L1norm and L2norm of example 1
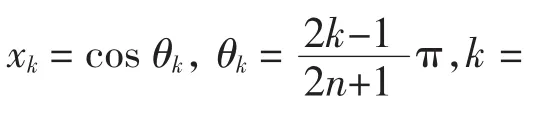
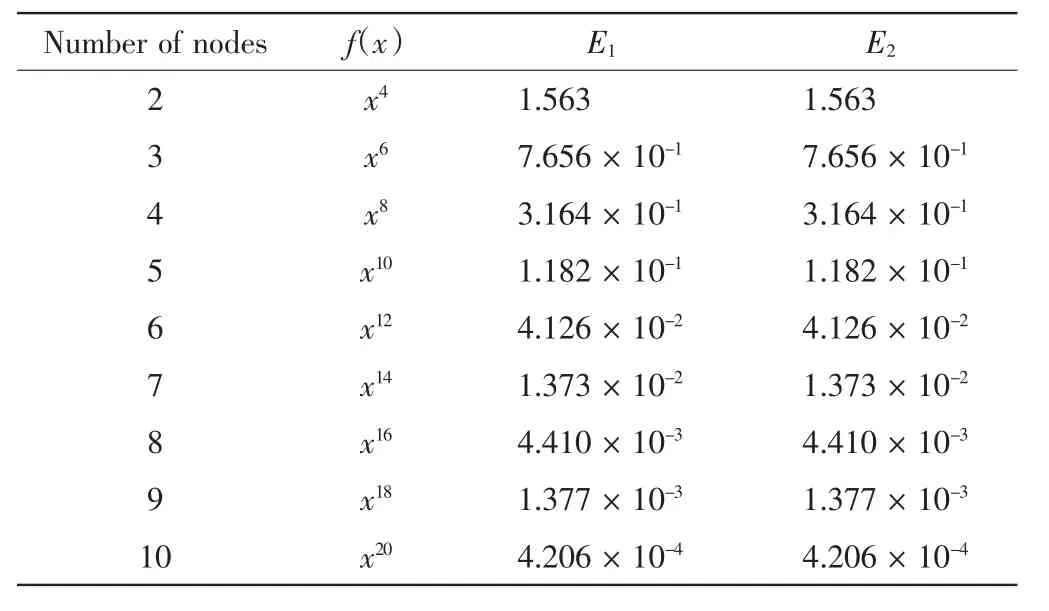
表2 例2的Hn在最大范数下的逼近误差Tab.2 Approximate errors of Hnunder maximum norm of example 2
