数形结合在数学教学中的运用

山东省邹城市郭里中学 韩昌忠

中学数学与小学阶段相比，难度有了明显的提升，其中的知识内容更加抽象，需要学生有更强的思维能力。因此，本文针对数形结合在中学数学教学中的运用做出了进一步探究，有益于数学教学质量的提升。

在数学的日常授课过程中，教师需要利用合理的教学方式，帮助学生提升学习效果，其中，对于数形结合思想的应用，可以引导学生将图形与数字进行结合，使学生一起应用抽象思维和形象思维，以便对抽象的数学知识进行转化，提升对知识的理解。

一、以形喻数，提升学生对知识的理解程度

中学数学知识内容有了一定的抽象性，在以往的授课当中，教师有些忽视了学生的主体性，过于注重提升学生的知识记忆，应用满堂灌的授课方式指导学生学习。这样的学习过程中，学生始终处于被动的状态，在学习的过程中没有对知识有深入的了解，影响了学生的效果，长此以往，学生对于数学的学习会提不起兴趣，甚至讨厌学习数学。现在应用数形结合的思想，可引导学生应用图形对数字进行表述，将数进行转化，使其成为具体的形。所以，在教学中，教师可应用数形结合的思想，帮助学生学习数学知识，提升学习的效果。

例如：在《二次函数与一元二次方程》的授课中，需要学生通过探索，理解二次函数与一元二次方程之间的联系；能运用二次函数及其图象确定方程和不等式的解或解集；根据函数图象与x轴的交点情况确定未知字母的值或取值范围。为了帮助学生对知识点的记忆更加牢固，可通过练习题的形式，帮助学生巩固知识点，并应用数形结合的思想对问题进行判断和分析。

如：关于二次函数y=ax2+bx+c的图象有下列命题，其中假命题的个数是（ ）

①当c=0时，函数的图象经过原点；

②当b=0时，函数的图象关于y轴对称；③函数的图象最高点的纵坐标是；

④当c＞0且函数的图象开口向下时，方程ax2+bx+c=0必有两个不相等的实根。

A.0个 B.1个 C.2个 D.3个

解：①二次函数y=ax2+bx+c中，令x=0代入得到y=c=0，即函数图象经过原点，正确；

②当b=0时，函数是y=ax2+c，函数的图象关于y轴对称，正确；

④图象的开口向下，则a＜0，又c＞0，Δ=b2-4ac＞0，方程必有两个不相等的实根，正确。

综上，是假命题的是③。所以答案为B。

二、解决问题，帮助学生简化解题思路

学生对于数学的学习，需要学会应用灵活的解题方法，以便简化解题思路，提升解题效率。因此，在日常授课的过程中，还引导学生学习不同的解题思路，以便学生能够应用学到的知识对数学问题进行解决。这也是数学授课的重点教学目标，与学生的知识应用能力会起到重要的帮助作用。有些数学问题比较复杂，学生对于解题思想不会灵活应用，影响了解题的效率。现在应用数形结合的思想，可简化复杂难懂的问题，帮助学生对问题进行深入的探究。

（1）请你用树形图或列表法列出所有可能的结果；

（2）现制定这样一个游戏规则：若所选出的a、b能使方程ax2+bx+1＝0有两个不相等的实数根，则称甲胜；否则乙胜。请问这样的游戏规则公平吗？请你用概率知识解释。

在学生分析的过程中，教师可以应用数形结合的思想引导学生进行分析，首先根据题意画出树状图，然后根据树状图即可求得所有等可能的结果；之后利用一元二次方程根的判别式，即可判定各种情况下根的情况，随后利用概率公式即可求得甲、乙获胜的概率，比较概率大小，即可确定这样的游戏规是否公平。

解：（1）画树状图，得：

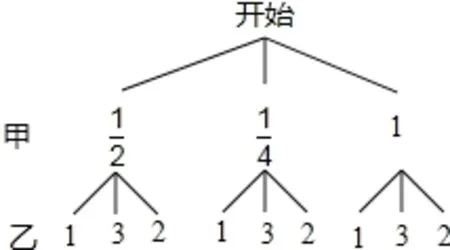
总之，在数学日常授课的过程中，对于数形结合思想的应用有益于学生学习质量的提升，帮助其提升对知识的理解程度、简化问题的难度等，以便为学生之后的数学学习打下良好的基础。