高中数学解题的几个误区
2019-03-25广东省高州市第二中学卢楚军
广东省高州市第二中学 卢楚军
从教高中数学多年,每学期初的第一节数学课,我给学生讲的一句话就是:要解好一道数学题、一道高考题,除了要熟悉知识点和解题方法外,在解题过程中也要尽量避免走进解题的误区,才能拿到一个好的分数。对于学生的解题误区,我有以下一些体会。
一、审题时没有抓住题目关键性词语
在高中数学学习过程中,审题是解决问题的基础和先导,是正确做题不可缺少的环节。数学审题,即对数学题目提供的情节内容和数量关系进行分析和理解。但是在平时的教学中,在作业试卷批改当中,我总会遗憾地发现,学生不是看错了数字,就是没弄明白题目的意思,或者不能挖掘出题目条件与结论的联系,还有一些学生容易凭记忆做题。课堂会做题,课后或者考试不会做题。当试卷作业发回来或者老师评讲时,把题目再细心读一读,很多同学就又会把题目解对了。所有这些,都说明了学生审题能力的薄弱。
审题的重点在于准确理解题意,与此同时,还需要对题意中的条件、定义、概念、定理、公式等进行快速理解,抓住题意中的关键性词语,防止出现解非所答。例如,平时选择题中题干要求学生选择“错误”的选项,很多学生根本没有认真读题,不知道要他做的是什么事情,自以为是地认为是选择“正确”的选项,那样很难找到正确的答案。另外,很多学生对一些题目的条件和涉及的知识点联系不起来。例如:
(1)若曲线x2+y2+a2x+(1-a2)y-4=0关于直线y-x=0的对称曲线仍是其本身,则实数a=( )
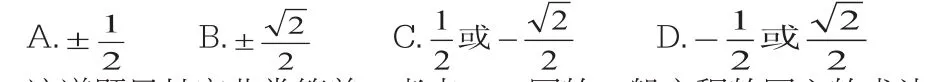
这道题目其实非常简单。考点一:圆的一般方程的圆心的求法。考点二:一个圆关于直线的对称圆的问题。但是做错的学生很多,原因一是同学们语文基础比较差,没有理解这句话的主谓结构,不明白题目让他做什么;原因二是学生不能将圆的结构、方程等知识点与题目条件很好地联系起来。对于这类型题目,我在课堂上让学生首先对这个题目多读几遍,针对关键词语“仍是其本身”,学生要准确理解含义“是同一个圆,此圆的圆心在直线y-x=0上”,然后与圆的一般方程的圆心求法联系起来,那样学生动笔起来,果然做对了。
(2)已知 sin(α+β)=0,tanβ=2,求 tanα= 。
这是一道三角函数求值的问题,考点是正切两角差公式和特殊值的三角函数值。很多学生不会做,原因是他们没有留意到题目中条件与问题中的角的关系。实际上,细心分析题目的学生会发现,条件中角α+β与β与问题中的α有着紧密的联系,就是(α+β)-β=α。那么要求tanα,只需求tan[(α+β)-β]就可以了。这道题的关键性词语就是三个角“α+β,β,α”。只要看出它们之间的联系,问题就会迎刃而解。另外,这道题的关键性词语还可以是“sin(α+β)=0”,因为 α+β=kπ,则有 α=2kπ-β,即有 tanα=tan(2kπ-β)=-tanβ=-2。这个方法要求对于特殊角的三角函数值要非常熟悉。课堂上,我对于这种题型,尽量让学生总结归纳审题规律,找出题目中可能有用的关键性词语,分析题目条件中的角和问题中的角的关系,那么下次碰到同一个类型的题目,读题的时候就自然而然地联想到它们的关系了。当然,要提高审题的准确性,前提条件是要对数学知识点非常熟悉,能够把问题中所涉及的条件和定义、概念、定理、公式等联系起来。
二、解题时思维不够严密,不能充分挖掘条件
很多学生由于思维不够严谨,对题意中的隐含条件没有进行充分的挖掘。教师在教学过程中需要注重对学生解题思维严谨性的训练,教会学生从整体上把握题意的主旨以及挖掘题目中隐含的条件。例如:

以上例子给我的启示就是,在数学教学课堂中,需要注重数学问题陈述及表现形式的多样性,积极引导学生思考,从知识点的整体去考虑,达到解题的严密性,进而提高学生的解题能力。在这个问题上,我采取了一种策略,即“错解剖析”——给学生进行题目讲解,在讲解过程中故意设置错误,让学生给我指出讲解过程中出现的错误,让学生反串教师的角色,从另一个角度考查学生对知识的掌握情况,从而养成挖掘题目条件的好习惯。例如:

学生对结论的可靠程度提出怀疑,在独立分析的基础上,进行“错解剖析”。灵活运用三角函数的单调性来确定三角形内角的取值范围这个隐含条件,严密论证了三角函数值取值的可能性。
三、解题时不够灵活,不注重转化思想
数学解题很讲究灵活性,对于复杂的问题,如果能够把问题转化,可使问题的形式朝有利于计算、推理、证明或能更好地运用定理和法则来解决问题的方向进行。例如:
方程sinx=lgx的解有( )个。
A.1 B.2 C.3 D.4
学生习惯对方程进行求解,若方程无法求解,则令学生手足无措。需要引导学生思考角度的变化:此题本质为求方程组解。运用数形结合思想转化为求函数图象交点问题,寻求几何性质与代数方程之间的内在联系。通过知识串联、横向沟通牢牢抓住事物的本质,在思维深刻性的基础上,思维灵活性才有了用武之地。所以,当学生读这个问题的时候,就应该发散思维,从题目形式思考,一个为三角函数,一个为对数,考虑到可以将方程问题转化为函数问题。
在课堂教学中,也要注重问题的转化思考。我经常采用的是“例题变式”——从例题入手,不断进行条件的变化,寻求解题结论的不同之处;变换结论,寻求条件的不同之处;变换提出问题的背景,寻求多题一解;变换问题的思考角度,寻求一题多解……以此来培养学生灵活的思维。例如:


以上只是我在教学过程中发现学生解题的一些误区,这些在我培养学生解题能力的策略制定上有指导性的作用。近年来,在数学教学过程中对学生进行针对性训练后,不仅学生的解题能力均得到了较大程度的提高,而且学生对数学学习的兴趣也得到了较大程度的提高。我的很多学生进入大学甚至走上工作岗位之后,仍常来信表示虽然很多数学知识已经遗忘,但学到的数学思维方式却在日后的工作、学习及生活中发挥着积极的作用。目前国内的课程教材在不断进行改革,我要继续探索下去,以求获得更多的收获。
