数学课堂“钻井式”教研的教学片段与评析

楼旭珍

（浙江省金华市东阳市实验小学，浙江 金华 322100）

这次活动的内容是“加法交换律和结合律”，参加活动的教师先独立备课，再确定其中一位教师上前测课；课后教师集体评议，修改教案，再次抓阄确定一位教师上研究课；然后进行第二轮评课，整理教案，完成展示课。下面就三次课堂设计的一些教学片段，来谈谈我的几点认识。

前测课教学片段：

师：（出示主题图）根据图中的信息，你还能提出哪些数学问题？

生：参加跳绳的和踢毽子的共有多少人？

师：怎样列式计算？[根据回答，教师板书：（13+45）+15与13+（45+15）]

师：这两道算式的和不变，加数也不变，像这样的两个算式，可以组成一个等式，即（13+45）+15=13+（45+15）

师：像这样的等式你还能举例吗？（学生举例略）观察这些算式，你有什么发现？

生：三个加数没变，加数的位置也没变，但运算的顺序变了，最后的结果却没变。

这就是我们今天要来学习的一个重要运算定律——加法结合律。

师：你能不能用一个算式把这个规律概括出来？

生：（a+b）+c=a+（b+c）

评析：教师利用主题图引出加法的运算定律，帮助学生理解运算定律，并且运用所学的定律解决生活中的实际问题。但课上完了，还有学生说两个数相加就运用了加法交换律，三个数相加就是运用了加法结合律；甚至有学生回答说有括号就是运用了加法结合律，没有括号就是运用加法交换律。究其原因，在于教师没有充分引导学生观察两种运算律的本质特征，没有让学生真正经历规律的探究过程。再者，运用简单归纳推理时，不能仅凭简单的几个例子就得出结论。

经过教师们的深入讨论，认为在“加法交换律和结合律”的教学中，教师应注重引导学生经历质疑、猜测、观察、举例、验证等数学学习方法运用的全过程，然后归纳提升这些方法，使学生始终处于一种思考、实践、再思考的境地，最终学到终身受益的数学思想和方法。基于以上认识，于是有了第二次教学。

研究课教学片段：

师[出 示（2+3）+5 与2+（3+5）；（13+45）+15与13+（45+15）；（7345+63）+37与7345+（63+37）三组算式]：分别计算这三组算式，看看是否相等，为什么？

生：不论谁先算了，得数还是一样的。

师：谁听明白了？

生：三个加数没变，加数的位置也没变，但运算的顺序变了，最后的结果却没变。

师：是否所有三个数相加，都有这样的规律呢？请举例验证。

生：经过验证，发现所有的加法算式中都有这样的规律。

师：你能不能也用一个算式，来表示这个规律呢？

生：（a+b）+c=a+（b+c）

师：加法交换律和结合律有什么相同点和不同点？

……

评析：研究课中教师有意识地出示三组算式：从一位数到两位数再到三位数，由简到繁，由易到难，层层递进，让学生观察其特点，判断每组算式之间能否用等号连接，并让学生通过计算验证猜想。回顾整个教学过程，不难发现：教师力图让学生经历“观察——猜测——举例——验证”的学习过程，自主探索加法运算规律，使学生在合作与交流中，对运算律的认识由感性逐步发展到理性，合理地建构知识。但是，教学时教师不够放手，始终带着学生一小步一小步地往前走，导致学生在后面的学习中兴致明显不如先前。本节课在学习加法交换律之后，应指导学生归纳学习方法；教学加法结合律时，应引导学生运用前面的方法自主学习。

展示课教学片段：

师：刚才我们是怎样学习加法交换律的？

生：先猜想、举例、验证，最后得出结论。

师：接下来，我们就用“猜想——举例——验证”的方式，小组合作研究加法的另一种运算定律，组长把研究结果记录在表格中。（表格如下）：

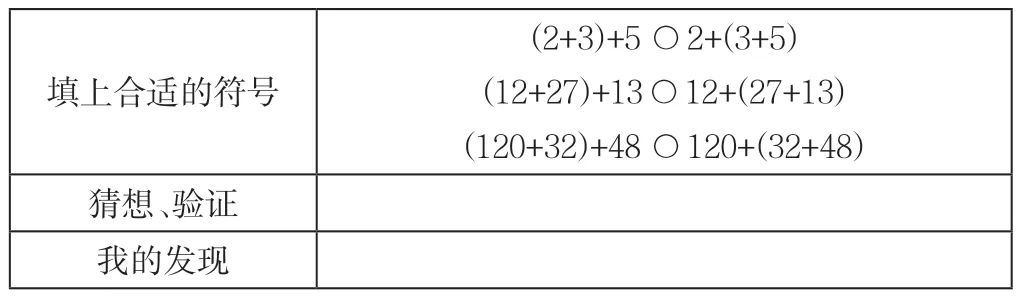
填上合适的符号（2+3）+5 ○2+（3+5）（12+27）+13○12+（27+13）（120+32）+48 ○ 120+（32+48）猜想、验证我的发现

评析：在教学加法交换律之后，组织学生小组合作，探索加法结合律。教学中安排了三个层次，通过猜测与探索、观察与分析、归纳与验证等一系列数学活动，使学生从中认识到数学思考过程的条理性和数学结论的确定性，培养了学生数学知识的迁移能力，提高了学生数学思考的能力。

结语：不难看出，经过一次次的教学、一次次的讨论和反思，我们对于本节课的理解越来越深入。围绕一节课，进行“前测、研究、展示“的研究，好像勘探钻井一样，不断地深入，丰富了教学智慧，是推进校本教研、促进教师专业化成长的好形式。