基于猴群算法的斜拉桥测点优化布置研究
2019-03-23栾守领
杨 康,李 铎,栾守领
(长安大学 公路学院,陕西 西安 710064)
0 引言
随着近年来桥梁工程的快速发展,大跨桥梁结构日益涌现。由于各种内外因素的影响,这些结构在服役期间不可避免地会出现不同程度的损伤,因此对大型构筑物建立实时监测的健康监测系统(SHM)就显得非常必要[1]。而传感器测点布置问题关系到获取数据的有效性和健康监测系统的成本,是整个健康监测系统中很关键的一部分。对传感器测点的数量及布置进行科学分析、优化处理,保证获取到的桥梁结构动态信息全面可靠,是对桥梁服役状况做出准确评估的基础。
目前,传感器优化布置的计算方法主要有如下几种。有效独立法[2],包括逐步消减法和逐步累积法的序列法[3],遗传算法[4]和模拟退火法的随机类方法等。Zhao et al[5]提出的猴群算法适用于求解多变量多峰函数的优化问题,对于测点较多的大型结构传感器测点优化布置问题有着独特的优势。张旭东[6]将其应用于高层建筑的传感器布置中,但目前很少有将其应用于桥梁健康监测的传感器布置中,特别是该算法对于斜拉桥传感器优化配置问题的适用性有待验证。
2 模态选择
2.1 工程概况及理论模型
某斜拉桥为双塔PC斜拉桥,采用半飘浮体系。跨径布置为60+150+380+150+60=800 m。采用有限元专用计算软件MIDAS/Civil建立全桥有限元模型。主梁、主塔、辅助墩、过渡墩采用梁单元模拟,斜拉索采用恩斯特公式修正的桁架单元模拟。全桥共1 045个节点,702个梁单元、232个桁架单元。有限元模型如图1所示。
2.2 模态振型选择
通常基于振型向量正交原理来确定传感器位置。而振型是由多个模态组成的,选择不同的模态振型会对传感器位置布置产生直接影响。以往多选择低阶的模态振型来解决测点优化问题。李晓等[7]在连续刚构桥梁的测点布置中仅考虑了前4阶竖向振型。斜拉桥跨度较大、振型更加复杂,模态比较密集,一些高阶模态对结构的振动有较大影响,不能忽略[8]。简单地选取前若干阶振型进行研究并不可取。由于斜拉桥主梁节点多,模态阶数过于繁多,可先确定待选目标模态阶数,再根据监测目标要求从中进一步选取计算用的模态振型。借鉴孙小猛[9]提出的Fisher信息矩阵的2-范数来确定待选模态阶数,先确定前10阶模态作为待选取目标模态振型。然后,依据振型参与质量和振型主方向从其中选取y和z方向的6阶模态作为计算模态振型。
Fisher信息矩阵可以表示为

式中,QΦ为基于振型的Fisher信息矩阵;Φ为振型矩阵。
Fisher信息矩阵QΦ反应了结构模态振型反应的敏感性[9]。由于模态振型具有正交性,对于目标模态数为m的Fisher信息矩阵QΦ可写为
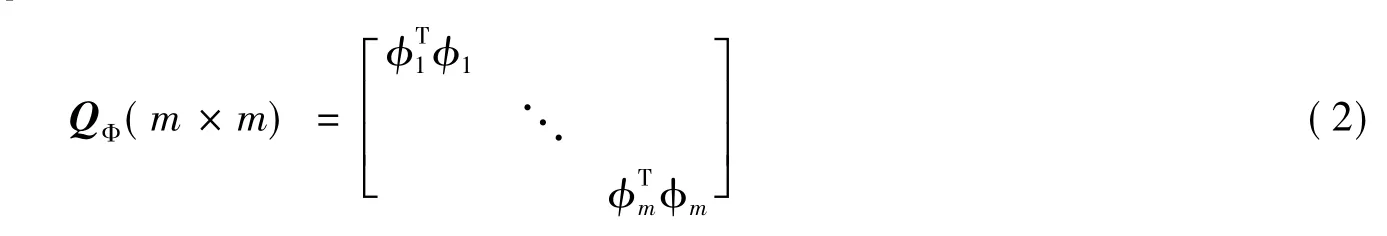
若拥有m阶模态的Fisher信息矩阵为Qm,其二范数为‖Qm‖2,则其在前i阶和i+1阶模态上的变化率记为ROC(rate of change)。则有
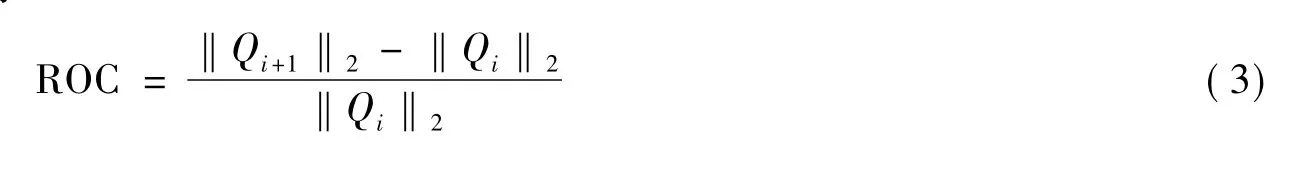
式中,i为计算采用的模态数。
ROC值随采用的模态数i值变化,并随i的逐渐变大趋近于零。当ROC趋于稳定且其值很小时可认为前i阶模态包含了足够多的结构模态信息。布置传感器时可只考虑这些模态,从而缩小了选择范围,简化了计算分析。
依据结构特征值分析结果,计算主梁495个节点前40阶振型模态的Fisher信息矩阵,得到Fisher信息矩阵2-范数在前40阶模态变化率见图2。
由图2可知随着i值的不断变化,ROC值不断变化,当i超过10时,ROC接近于零,且趋于稳定。因此可认为前10阶模态包含了该桥足够多的模态信息,可作为有待进一步筛选的目标模态。提取其前10阶模态振型的方向、频率及振型参与质量见表1。
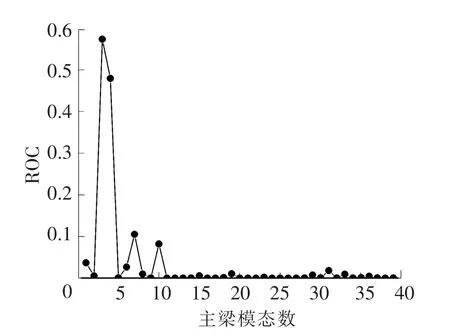
图2 主梁ROC曲线图
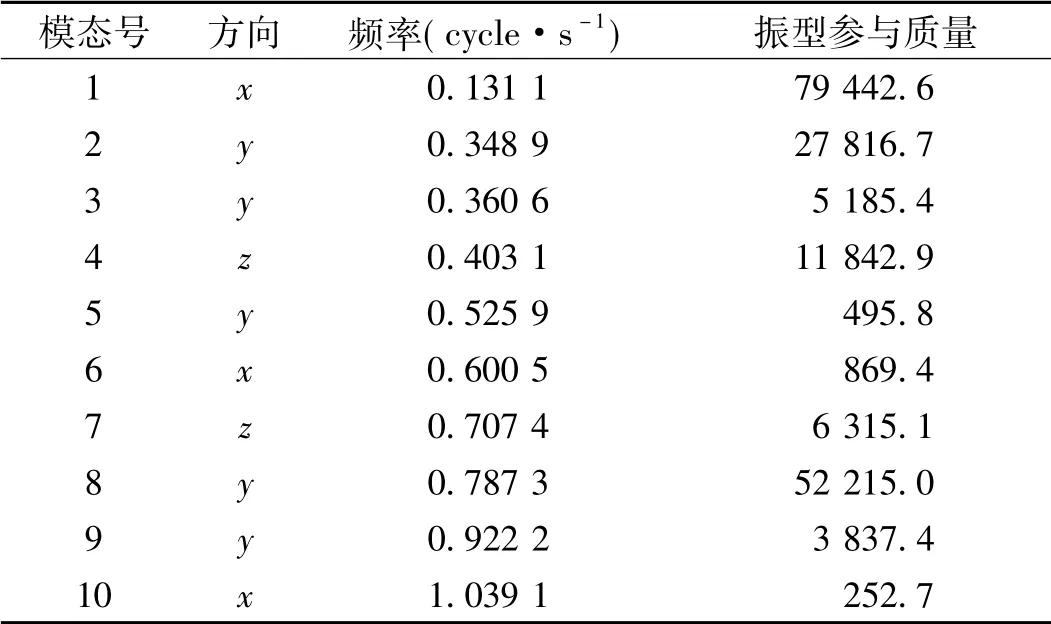
表1 前10阶模态振型及其特性
由于现实中更关心主梁竖向和横向振动,所以选取表1中y和z方向的振型。其中2,3,4,5,7,8阶模态振型的振型参与质量之和为103 870.6,占前10阶中所有y,z方向模态振型参与质量总和的96.4%。由此可认为第2,3,4,5,7,8阶模态振型包含了竖向与横向振动足够多的特征值信息。因此选取第2,3,4,5,7,8阶模态作为最终分析的目标模态,这样既可以保证拥有充分的结构特征值信息,又不至于数据过多造成计算困难。
3 猴群算法
3.1 猴群算法的原理
猴群算法是一种模拟猴群爬山的群智能算法[10],主要用于解决带有连续变量的全局优化问题,其基本思想是模拟猴子爬山的爬、望和跳3个过程,以此进行迭代的全新智能计算[11-13]。为找出整个域内的最值点,假定有m群猴子,每群n只,共m×n只猴子爬山。通过初始化每只猴子从自己所处的随机位置出发,以特定步长a往上爬,当爬到所处领域最高处时,以视距b向周围瞭望,如果在周围能找到比自身位置更高的山峰则跳到此山峰,然后继续进行爬过程,如此循环迭代。
3.2 猴群算法步骤
(1)编码和目标函数。假设共有N个传感器待选位置,并对其进行编码1~N作为附加码。变量码采用二进制0或1,表示对应位置是否布置传感器。将模态置信准则(MAC)作为目标函数。

式中,i和j分别表示模态矩阵的第i、第j列。为保证振型向量的线性无关,MAC矩阵非对角线元素的值越小越好。MAC矩阵非对角元的最大值越小,表明其相应的振型模态向量的空间交角越大,也越容易识别两阶振型模态[14-15]。
(2)初始化。随机生成m×n行变量码,计算每只猴子的适应度(同式(1)),并排序。把m×n只猴子平均分配到m个猴群中,将适应度好与适应度差的个体均匀地分散到各个猴群中。
(3)爬过程。用向量Xi=(Xi,1,Xi,2,…,Xi,n)表示第i只猴子对应变量码值为1的位置,在区间[-a,a]上产生随机整数向量ΔXi=(ΔXi,1,ΔXi,2,…,ΔXi,n),由Xi+ΔXi得到猴子爬之后的新位置,并计算相应的目标函数判断是否代替原来的位置,循环该过程直到达到预定的次数为止[9]。
(4)望过程。定义猴子视距为b,在区间[Xi,j-b,Xi,j+b]上产生随机整数yi,j,由此得到新的向量即为新位置。计算猴子新位置的目标函数,变好则替换原来的位置并返回爬过程,否则重新生成yi,j,直到达到设定的循环次数为止。
(5)跳过程。定义跳区间为[-c,c],在跳区间内产生随机数θ。计算出该猴群位置向量的各分量重心pj=其中j∈(1,2,…,n)。再计算猴子的新位置:Xi,j=Xi,j+roung(θ|pi-Xi,j|)。计算猴子新位置的目标函数,变好则替换原来的位置并返回爬过程,否则重新生成pj计算,直到达到设定的循环次数为止。
(6)最后,在所有猴群中选择最优的一个个体作为测点布置的位置。
猴群算法流程见图3。
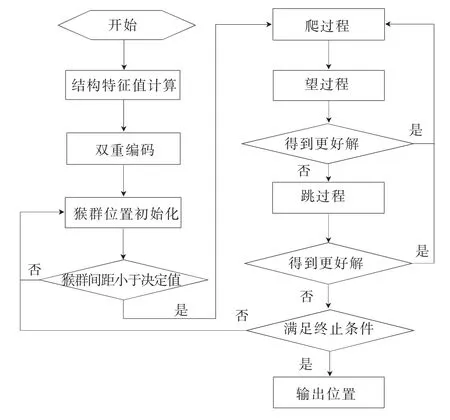
图3 猴群算法流程图
4 传感器优化布置
4.1 传感器数量
为确定传感器测点布置,首先要确定传感器测点个数。斜拉桥跨径大,主梁节点多,需要通过多次迭代计算以确定传感器个数。以MAC准则为目标函数,传感器个数为自变量,分别通过有效独立法、遗传算法和猴群算法进行迭代计算。有效独立算法是传统的优化算法,只需改变自变量直接进行计算。而遗传算法[14]和猴群算法都是智能算法,需要设定一些控制参数。该斜拉桥模型主梁共495个节点,即495个测点可选位置。设定猴群算法中猴群数为10,每个猴群中猴子数为10,爬、跳、望各迭代400次,爬步长为1,望步长为2,跳步长为3。遗传算法中,种群个体数为100,变异概率0.5,杂交概率为1。两种算法的迭代次数均设为100次,结果见图4。
由图4可知,随传感器数量的变化,猴群算法计算所得的MAC非对角元最大值均明显小于有效独立算法和遗传算法的计算结果,体现了猴群算法在传感器优化配置中的优越性。同时3种算法的计算结果在自变量变化范围内都出现了先减小再增大的变化规律,由此可以确定传感器的数目。猴群算法、遗传算法和有效独立算法的目标函数分别于14,14,12个测点数目时取得最小值。因此,确定最终传感器的数目为14个。
4.2 两种智能算法的比较
通过改变迭代次数,以MAC矩阵非对角元最大值为标准,比较遗传算法与猴群算法的优劣。测点数目由上节设置为14个,其它培训参数设置如上节,结果见图5。
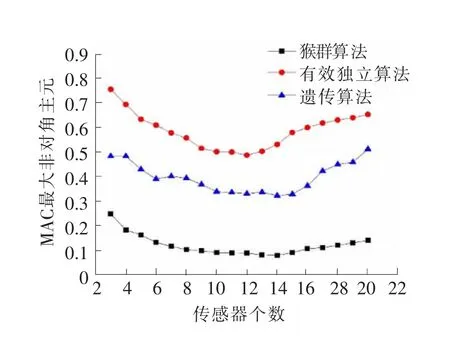
4 MAC非对角元最大值随传感器个数变化图
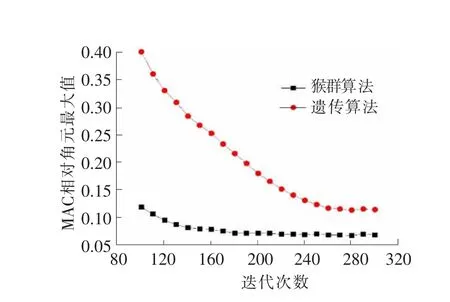
图5 MAC最大非对角元随迭代次数的变化
比较两种算法,可以发现随着迭代次数的增多,目标函数值不断下降,并趋于稳定。整体而言,猴群算法计算所得的MAC矩阵最大非对角元明显小于遗传算法的结果,具有更高的精度。且猴群算法迭代190次左右趋于收敛,收敛后MAC最大非对角元为0.067;遗传算法迭代270次收敛,收敛后MAC最大非对角元为0.112。对比可知猴群算法收敛速度更快,效率更高。
此外,一般对于中小跨径结构,可认为MAC矩阵最大非对角元小于0.05时,用来计算测点位置的各阶模态正交性较好,容易分辨。也有学者建议,对于比较复杂的结构,这个值最大可以放宽至0.25。计算的结果显示,采用猴群算法可将该值控制在0.1以下,可认为大跨结构MAC最大非对角元小于0.1时测点位置模态正交性较好。
4.3 测点优化结果
设定迭代200次,猴群算法计算所得的测点位置经优化后的结果见表2和图6。

表2 传感器位置优化结果
结果显示,应用猴群算法所得的传感器优化位置,除个别点外,整体分布均匀。
基于上述测点位置算得的MAC矩阵值见图7。
由图7可知,通过猴群算法优化所得的测定位置MAC矩阵所有非对角元素均相对较小,由此印证模态的线性无关性良好。也说明了优化后测点位置的合理性。
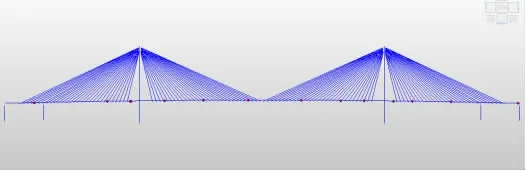
图6 测点位置示意图

图7 猴群算法计算所得的MAC矩阵值
5 结论
(1)大跨结构节点较多,因此需要相对较多的传感器来获取更为全面准确的结构参数。同时由于结构复杂,计算的MAC矩阵最大非对角元也相对较大,一般可认为对于大跨结构该值小于0.1时用来计算测点位置的模态正交性较好。
(2)猴群算法作为一种智能算法,由于猴群位置初始化过程具有一定随机性,所以最终得到的测点位置的结果不是唯一的,应进行多次计算,选取最优解以获得最佳测点位置。
(3)猴群算法收敛速度快,计算精度高,适用于大跨斜拉桥的测点优化问题。
(4)调试过程中,猴群算法计算所得的少数测点位置出现了堆积现象。为避免此类现象,有待提出改进的猴群算法应用于大跨结构健康监测的测点优化中。
