负弯矩荷载下钢-混凝土组合梁抗弯刚度研究

刘劲，丁发兴，蒋丽忠，付磊，黄琰

负弯矩荷载下钢-混凝土组合梁抗弯刚度研究

刘劲1, 2，丁发兴2，蒋丽忠2，付磊2，黄琰1

(1. 湖南城市学院 土木工程学院，湖南 益阳 413000；2. 中南大学 土木工程学院，湖南 长沙 410075)

针对负弯矩作用下钢-混凝土组合简支梁的抗弯刚度，考虑剪力连接度与纵横向配筋率等参数的影响，进行13根负弯矩作用下钢-混凝土简支组合的抗弯刚度试验研究，并运用ABAQUS有限元软件对负弯矩作用下钢−混凝土组合梁的力学性能进行模拟，其中栓钉分别采用梁单元和弹簧单元2种建模方法。在试验验证的基础上，通过足尺算例探讨剪力连接度、栓钉布置、栓钉直径、加载位置、纵筋率及跨度等参数对钢−混凝土组合梁负向抗弯刚度的影响规律。研究结果表明：剪力连接度对刚度影响最大，纵筋率的影响其次，其余参数影响不大。结合试验研究与理论分析，建议钢−混凝土组合梁负向抗弯刚度仍按规范《钢结构设计标准》(GB 50017—2017)提供的表达式，提出考虑混凝土翼板0.6c有效厚度并计入钢梁与钢筋等抗弯刚度贡献的负弯矩折减刚度法，该方法与现有的钢-混凝土组合梁负向抗弯刚度计算公式相比精度较高。

钢−混凝土组合梁；抗弯刚度；有限元；剪力连接度

钢−混凝土组合梁具有承载力高、刚度大、截面尺寸小和施工快速便捷等特点，在建筑与桥梁结构中得到广泛应用[1]，工程中常用的钢−混凝土组合梁主要有简支梁、连续梁和刚构梁，当前学者们对组合梁正弯矩区受力性能的研究涉及较多，如聂建国等[2]推导了各荷载作用下钢−混凝土组合梁因滑移效应引起的附加挠度计算公式，提出了钢−混凝土组合梁的折减刚度法，并为中国规范《钢结构设计规范》(GB 50017—2017)[3]采纳，其他学者如蒋丽忠等[4−7]也对组合梁正弯矩区的刚度与承载力进行研究。工程中钢−混凝土组合连续梁与刚构梁的负弯矩区同样存在刚度、裂缝和承载力计算等问题，当前各学者对负弯矩区钢−混凝土组合梁的力学性能研究相对较少[8−14]，研究重点主要体现在承载力和裂缝宽度等指标，对抗弯刚度计算方法的研究较少，而各国规范[3, 15−16]建议采用换算截面法来计算钢−混凝土组合梁负向刚度，即仅考虑钢筋和钢梁形成的组合截面而不考虑受拉区混凝土的作用，聂建国等[17]建议不考虑受拉区混凝土板对负向刚度的贡献，提出考虑钢梁与混凝土板之间滑移以及混凝土与钢筋之间黏结滑移的钢−混凝土组合梁负向刚度计算公式。然而部分现有试验结果[11]表明组合梁负弯矩区刚度将大于只考虑钢筋和钢梁形成的组合截面，因此正常使用极限状态下应考虑受拉区混凝土对钢−混凝土组合梁负向刚度的贡献。为完善钢−混凝土组合梁负向抗弯刚度的计算方法，本文在课题组已有研究基础上[18−19]，进行的工作如下：1) 进行13根负弯矩作用下钢−混凝土组合简支梁的抗弯刚度试验研究，探讨剪力连接程度、横向配筋率等参数对刚度的影响；2) 采用合理的材料本构关系，运用ABAQUS软件建立有限元精细化计算模型，在实验结果验证的基础上通过参数分析探讨剪力连接度、纵筋率、栓钉布置、栓钉直径、加载位置以及跨度等参数对钢−混凝土组合梁负向刚度的影响规律；3) 将试验结果、有限元计算结果、现行规范《钢结构设计标准》(GB 50017—2017)以及其他学者提出的负向刚度计算公式进行对比验证与分析，提出考虑栓钉滑移和混凝土板开裂影响的负弯矩荷载下钢−混凝土组合梁折减刚度法。

1 试验研究及有限元分析

1.1 试验制度与加载

课题组共设计了13组钢−混凝土组合梁试件，试件的截面及配筋如图1所示，组合梁试验加载装置如图2所示，试件信息见表1。表1中为组合梁计算跨径，c为混凝土板宽，c为混凝土板厚，s为钢梁高度，为栓钉连接件直径，s为栓钉屈服强度，t为混凝土板横向配筋率，l为混凝土板纵向配筋率，y为钢梁屈服强度，cu为混凝土抗压强度。

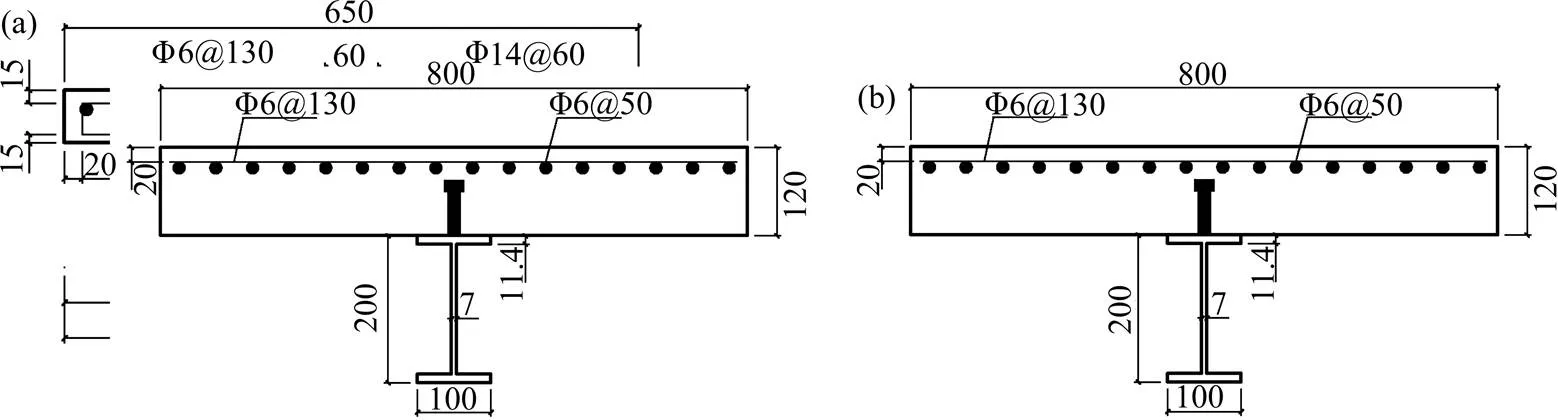
单位：mm

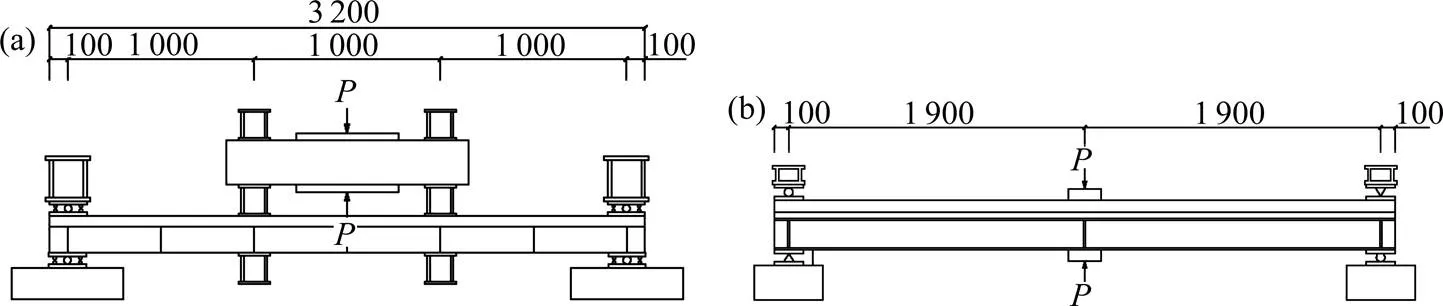
单位：mm

表1 组合梁试验参数

试件SCB8~9采用单调加载，其余11个试件采用竖向低周往复加载。试件的抗弯刚度值根据荷载−挠度关系曲线确定，取值为曲线上升段在0.4倍极限荷载对应的割线刚度。SCB1和SCB2试件沿梁长布置4个滑移千分表测量钢梁与混凝土板之间的滑移，布置5个百分表测量组合梁竖向挠度值。

1.2 有限元模型与验证

采用ABAQUS建模，混凝土采用三维实体单元(C3D8R)，钢梁采用壳单元(S4R)，钢筋采用桁架单元(T3D2)。材料本构关系及参数取值见文献[18−19]。栓钉模拟采用2种方法，一是梁单元(B32)模拟，栓钉与混凝土板为嵌入内置(embedded region)约束形式；二是弹簧(spring)模拟。采用弹簧来模拟栓钉时，弹簧的刚度由栓钉连接件推出试验和有限元模拟确定，非线性黏结−滑移关系曲线见文献[18]，钢−混凝土组合梁各部件单元类型如图3所示，网格划分、界面接触、加载控制方式和支承处理方式见文献[19]。

(a) 栓钉弹簧单元与混凝土板实体单元；(b) 栓钉梁单元与钢梁壳单元

负弯矩荷载下钢−混凝土组合梁的抗弯刚度的有限元计算结果与试验结果的比较见表1，()Test为实测值，()11为弹簧单元法计算值，()12为梁单元法计算值，13组试件实测值与弹簧单元计算值均值为1.003，离散系数为0.083；实测值与梁单元计算值均值为0.953，离散系数为0.085。典型试件SCB8的挠度、滑移以及应变计算结果与试验结果的比较如图4所示，可见：1) 荷载−挠度曲线加载弹性阶段曲线吻合良好，在弹塑性阶段及破坏阶段，理论曲线与实测曲线相比误差相对略大，可见本文建模方法对试验承载力及刚度模拟较好；2) 从试件荷载−梁端滑移曲线计算结果与试验结果比较可知，可知梁单元法计算的梁端滑移均小于弹簧单元法的计算结果，与相应的荷载−挠度曲线所得出的抗弯刚度规律一致；3) 试件跨中处纵向钢筋及钢梁底板应变测试(以拉为正，压为负)结果表明，2种建模方法计算结果与试验结果吻合较好。

(a) 荷载−挠度曲线；(b) 荷载−端部滑移曲线；(c) 荷载−应变曲线

1.3 负向抗弯刚度影响因素分析

负弯矩荷载作用下钢−混凝土组合梁抗弯刚度与换算抗弯刚度的关系如下：

(s)0(1)

式中：为钢−混凝土组合梁抗弯刚度；为抗弯刚度系数；(s)0为截面换算抗弯刚度；s为钢材弹性模量；为截面换算惯性矩，即不考虑混凝土翼板的抗弯刚度，仅计算钢梁与混凝土板中钢筋的抗弯刚度所得整个截面的惯性矩[3]。

《钢结构设计标准》(GB 50017—2017)[3]对钢−混凝土组合梁负弯矩区剪力连接度的计算方法如下：剪跨区内剪力s=ll，l为混凝土翼板内纵向钢筋的横截面面积，剪力连接度表达式为：

f(2)

式中：为组合梁栓钉实际数目；f为组合梁完全剪力连接时栓钉数量，f=su，u为单个栓钉的抗剪承载力，表达式如下：

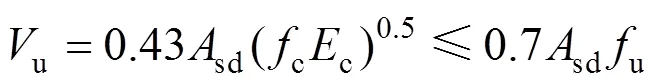
式中：sd为栓钉钉杆截面面积；u为栓钉抗拉极限强度；c为混凝土轴心抗压强度；c为混凝土弹性模量。剪跨区内剪力s取ss和cc的较小值，s为工字钢横截面面积；c为混凝土板受压区面积；位于负弯矩区段的抗剪连接件，其抗剪承载力乘以折减系数0.9。

1.3.1 剪力连接程度的影响

由SCB3~SCB7试件刚度测试结果对比可知，剪力连接度越大，刚度越大，刚度系数与剪力连接度之间的关系如图5所示。

图5 实测θ-η关系

1.3.2 配筋率的影响

图6所示为刚度系数随配筋率的变化规律，可见：SCB10~SCB13试件横向配筋率处于0.20%~ 1.18%之间，结果表明横向配筋率对各试件抗弯刚度影响较小，刚度系数处于0.83~1.15之间。

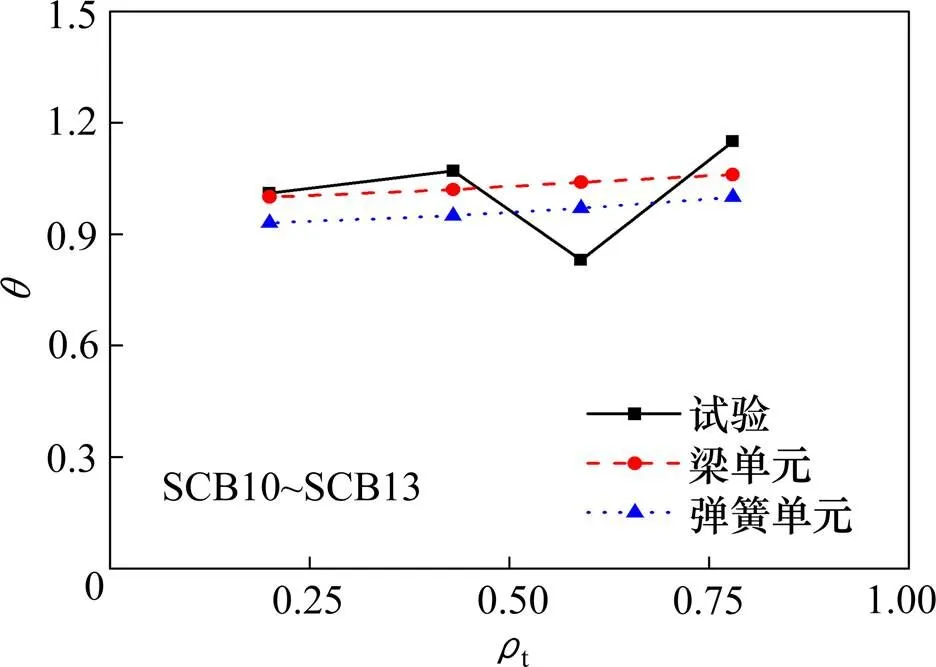
图6 实测θ-ρ关系

2 负向抗弯刚度计算结果比较与分析

2.1 规范方法

对于组合梁负向抗弯刚度()的计算，《钢结构设计标准》(GB 50017—2017)[3]、BS5950-3.1[15]和AISC-LRFD[16]规定，不计入受拉区混凝土板对刚度的贡献，但宜计入翼板有效宽度范围内纵向钢筋的作用，即在负弯矩区的抗弯刚度()等于考虑钢梁与混凝土板中钢筋的抗弯刚度，其表达式如下：

(s)0(4)

2.2 聂建国计算方法

聂建国等[17]考虑组合梁钢梁与混凝土之间的滑移、混凝土与钢筋之间黏结滑移效应的影响，而不考虑混凝土板对刚度的贡献，提出负弯矩区钢−混凝土组合梁折减刚度表达式如下：

式中：1为跨中集中荷载作用下附加挠度。

(6)

2为2点集中荷载作用下附加挠度。

,,,
,,,

为换算刚度下产生的挠度；为2点集中加载点间距的一半；为附加挠度；s为同一个截面的栓钉个数；r为纵向受力钢筋的直径；r为钢筋的数目；c为混凝土的抗压强度；为抗剪连接件纵向间距；s和r为钢梁截面形心和钢筋形心到到钢梁和混凝土翼板交界面的距离。

表2 钢−混凝土组合梁负向刚度计算结果与试验结果的比较

2.3 各方法计算结果与试验结果的比较

笔者收集了25组钢−混凝土组合梁负向抗弯刚度实测结果对有限元法计算结果进行验证，试件实测刚度与有限元法计算刚度的比较如表2所示，表2中()为抗弯刚度实测值，()11为弹簧单元法所得抗弯刚度计算值，()12为梁单元法所得抗弯刚度计算值，()2表示式(4)计算值，()3表示式(5)计算值。由表2可见：1) 试验值与弹簧单元模拟有限元值之比均值为1.022，离散系数为0.073，试验值与梁单元模拟有限元值之比均值为0.964，离散系数为0.079，可见2种单元法的有限元计算值都与实测值比较接近；2) 试验值与式(4)计算值比值均值为0.970，离散系数为0.180，而试验值与式(5)计算值比值均值分别为1.122，离散系数为0.160，式(4)与式(5)与试验值差别相对较大。

3 考虑滑移和开裂影响的负向抗弯折减刚度计算公式

3.1 剪力连接度对组合梁足尺模型算例抗弯刚度的影响

现有研究[1]表明剪力连接度对钢−混凝土组合梁刚度有着重要影响。本节以12 m跨度的钢−混凝土组合简支梁为计算对象，跨中加载，钢梁尺寸、混凝土翼板尺寸取值参考文献[3]，算例截面尺寸如图7所示。栓钉单排布置，直径19 mm，屈服强度为350 MPa，极限强度为455 MPa，纵筋率为2.56%，纵筋屈服强度为350 MPa。钢−混凝土组合梁模型有6种材料组合，分别为Q235匹配C30，Q235匹配C40，Q345匹配C40，Q345匹配C50，Q420匹配C50，Q420匹配C60，共计50组算例。50组12 m跨的钢−混凝土组合简支梁算例中剪力连接度对抗弯刚度系数的影响如图8所示，可知剪力连接度对钢−混凝土组合梁抗弯刚度系数影响较大，连接度越大，抗弯刚度系数越大，但当连接度超过2后抗弯刚度系数增长不明显。

单位：mm

有限元分析结果表明，当剪力连接度大于0.5之后，组合梁负向刚度系数大于1，由于规范[3]及聂建国等[17]计算方法均未考虑钢−混凝土组合梁中未开裂混凝土板对其抗弯刚度的贡献使得负向刚度系数均小于1，同时根据本文1.3节，SCB10~13试件的分析结果，钢−混凝土组合梁的刚度系数实测值也有大于1的现象。然而在钢筋混凝土结构中，《混凝土结构设计规范》GB50010—2010[20]考虑了受拉区混凝土开裂的影响，取钢筋混凝土构件的短期刚度为s=0.85，事实上钢−混凝土组合梁负弯矩区仅有部分混凝土开裂而都不考虑钢−混凝土组合梁中受拉区混凝土板的作用，尤如不考虑钢筋混凝土梁中受拉区混凝土对刚度的贡献，将使得计算刚度偏低，因此需要部分考虑钢−混凝土组合梁中混凝土板的抗弯刚度作用。

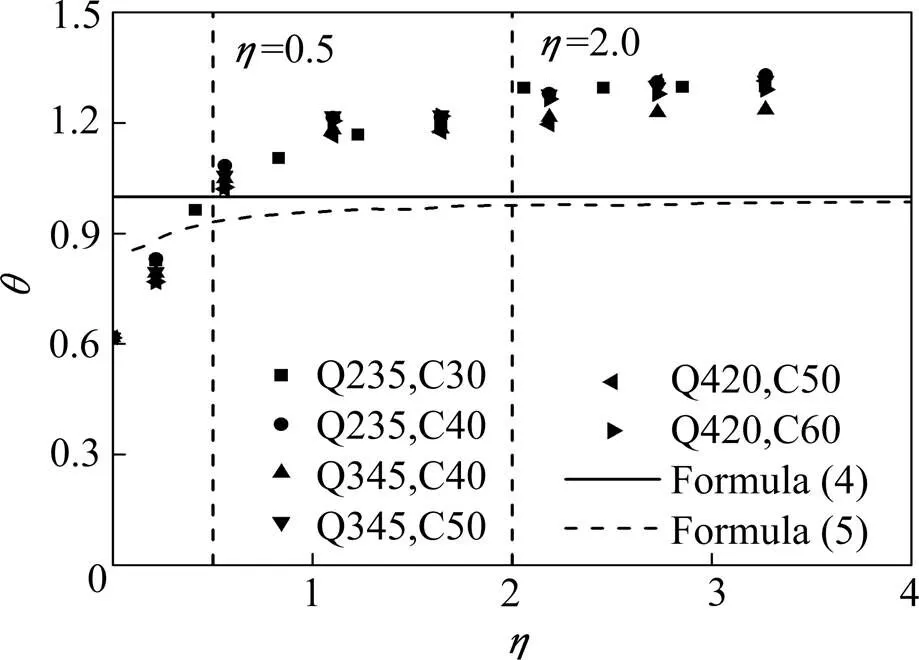
图8 θ-η关系

此外，《钢结构设计标准》(GB 50017—2017)[3]建议钢−混凝土组合梁正弯矩区抗弯刚度计算公式采用考虑栓钉变形引起钢梁与混凝土板滑移影响的折减刚度法，而针对负弯矩区钢−混凝土组合梁的抗弯刚度，笔者建议参考《混凝土结构设计规范》GB50010−2010[20]的条文，有如下考虑：1)混凝土板部分开裂后仍有0.6c(c为混凝土板厚度)范围内混凝土板(靠近钢梁侧)参与抗弯工作；2) 考虑纵向钢筋和钢梁对抗弯刚度的贡献。其表达式仍按《钢结构设计标准》(GB 50017—2017)[3]：

式中：

，，，
，，

为刚度折减系数；cf和分别为混凝土翼板和钢梁的截面惯性矩；c为钢梁截面形心到混凝土翼板截面形心的距离；为钢−混凝土组合梁截面高度；和为抗剪连接件刚度系数及纵向间距；s为抗剪连接件在一根梁上的列数；E为钢材和混凝土弹性模量的比值。

仍表示为抗弯刚度系数，即钢−混凝土组合梁负向抗弯刚度与换算抗弯刚度的比值，此时换算抗弯刚度考虑混凝土板开裂、纵向钢筋和钢梁参与抗弯工作。负弯矩荷载作用下50组12 m跨的钢−混凝土组合简支梁算例中剪力连接度对抗弯刚度系数的影响如图9所示，公式(4)，(5)和(8)均采用Q345匹配C40材料，可见在剪力连接度>0.5时折减刚度法仍可很好的反映剪力连接度对抗弯刚度系数的影响规律，而<0.5时的反常现象是由于=(0.4-3/()2)中，跨度和连接度变小时，刚度折减系数随之变小导致1/(1+)随之变大所致，因此笔者建议的考虑混凝土翼板0.6c有效厚度并计入钢梁与钢筋等抗弯刚度的组合梁负向折减刚度法具有物理意义与工程应用价值。

3.2 其他影响因素的探讨

以混凝土为C30、钢梁为Q235的12 m跨钢−混凝土组合简支梁为标准模型算例，栓钉直径19mm，栓钉屈服强度为350 MPa，极限强度为455 MPa，栓钉单排布置，分别考虑以下参数变化对负向抗弯刚度系数的影响：1) 栓钉双排布置；2) 栓钉直径，分别为13，16和22 mm；3) 加载位置，分别进行5/12，4/12和3/12跨集中加载；4) 计算跨度，分别为4，8，16和20 m；5) 纵筋率，分别为0.38%，1.28%和5.15%；表3所示为钢−混凝土组合梁参数。参数分析结果表明栓钉布置方式、栓钉直径、加载位置及方式、计算跨度对钢−混凝土组合梁负向抗弯刚度系数的影响不大，纵筋率对负向抗弯刚度系数影响较大，同等连接程度下，纵筋率越大，组合梁负向抗弯刚度系数略大，纵筋纵筋率对-关系的影响如图10所示。

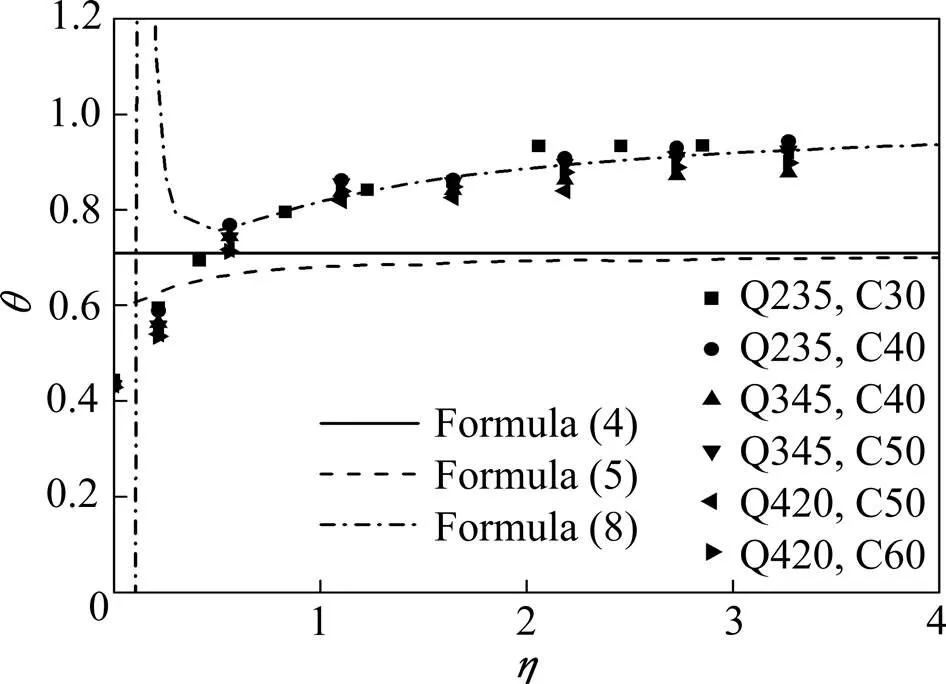
图9 θ-η关系

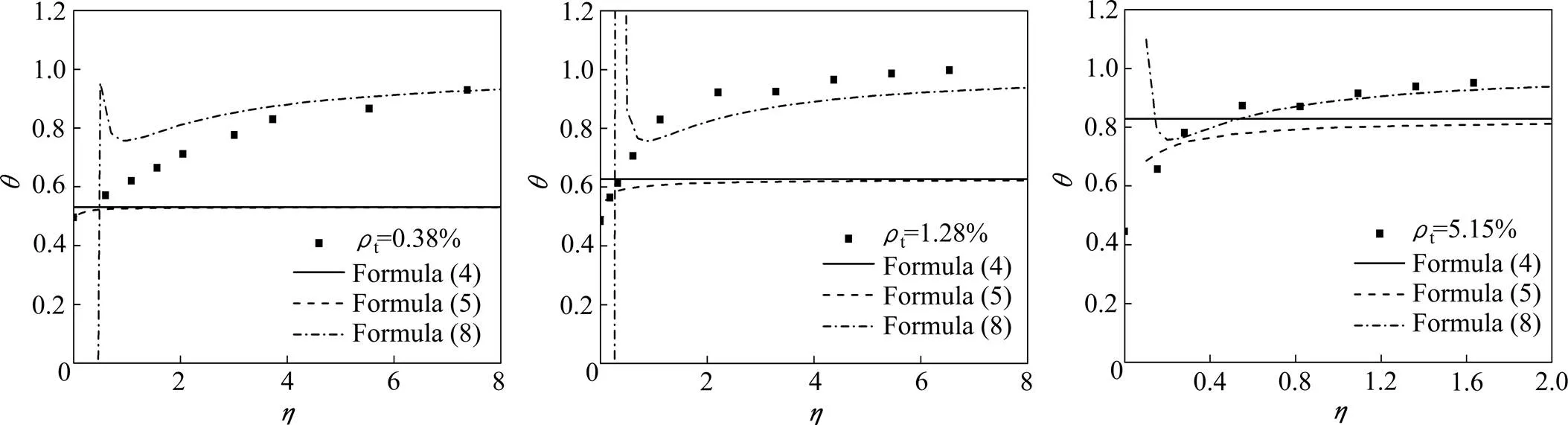
(a) ρt=0.38%；(b) ρt=1.28%；(c) ρt =5.15%

对于上述170组钢−混凝土组合梁模型算例，负向抗弯刚度有限元结果与式(4)，(5)和(8)的比较如表4所示，()4表示式(8)计算值，可见：1) 有限元计算结果与式(4)结果之比均值为1.193，离散系数为0.160，有限元计算结果与式(5)结果之比均值为1.239，离散系数为0.142；2) 有限元计算结果与式(8)结果之比均值为0.995，离散系数为0.092，而表2中有限元计算结果与式(8)结果之比均值为0.973，离散系数为0.138，可知式(8)计算结果与有限元计算结果及实测结果都吻合较好。

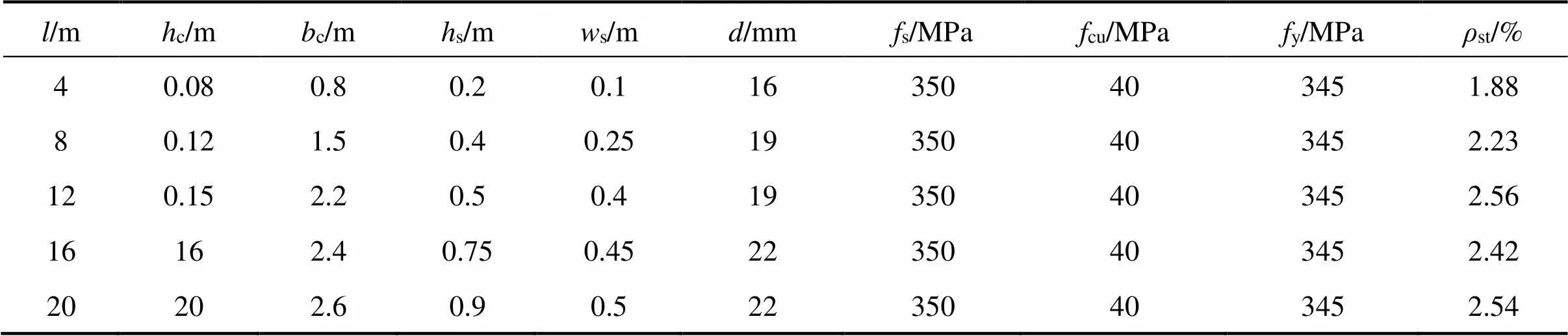
表3 钢−混凝土组合梁参数

表4 式(4)，(5)和(8)计算结果与有限元计算结果对比

4 结论

1) 完成了13根负弯矩作用下工字形钢−混凝土组合简支梁的抗弯刚度试验研究，探讨剪力连接度与横向配筋率等参数的影响，试验结果表明剪力连接程度对钢−混凝土组合梁负向抗弯刚度影响较大。

2) 运用ABAQUS有限元软件建立钢−混凝土组合简支梁有限元模型，栓钉分别采用梁单元和弹簧单元2种建模方法，2种方法分析结果与试验结果吻合良好，有限元分析结果表明剪力连接度是影响抗弯刚度系数的主要因素。

3) 根据有限元计算结果、公式计算结果、聂建国公式计算结果与试验结果的比较，在规范《钢结构设计标准》(GB 50017—2017)建议的已有钢−混凝土组合梁正向刚度计算公式基础上，考虑受拉区混凝土开裂而对公式中混凝土板厚度进行折减，建议了考虑混凝土板开裂折减效应、栓钉滑移效应以及纵向钢筋对抗弯刚度贡献的组合梁负向折减刚度法，该方法具有更为广泛的适用性。

[1] 聂建国. 钢混凝土组合梁结构试验、理论与应用[M].北京: 科学出版社, 2005: 1−308. NIE Jianguo. Test, theory and application of steel- concrete composite beam[M]. Beijing: Science Press, 2005: 1−308.

[2] 聂建国, 沈聚敏, 余志武. 考虑滑移效应的钢-混凝土组合梁变形计算的折减刚度法[J]. 土木工程学报, 1995, 28(6): 11−17. NIE Jianguo, SHEN Jumin, YU Zhiwu. A reduced deformation rigidty method for calculation of composite steel-concrete beams[J]. China Civil Engineering Journal, 1995, 28(6): 11−17.

[3] GB 50017—2017, 钢结构设计标准[S]. GB 50017—2017, Standard for design of steel structure [S].

[4] 蒋丽忠, 余志武, 李佳. 均布荷载作用下钢−混凝土组合梁滑移及变形的理论计算[J]. 工程力学, 2003, 20(2): 133−137. JIANG Lizhong, YU Zhiwu, LI Jia. Theoretical analysis of slip and deformation of steel-concrete composite beam under uniformly distributed loads[J]. Engineering Mechanics, 2003, 20(2): 133−137.

[5] 王景全, 吕志涛, 刘钊. 部分剪力连接钢−混凝土组合梁变形计算的组合系数法[J]. 东南大学学报(自然科学版), 2005, 35(增1): 5−10. WANG Jingquan, LÜ Zhitao, LIU Zhao. Consistency factor method for calculating deformation of composite steel-concrete girders with partial shear connection[J]. Journal of Southeast University (Natural Science Edition), 2005, 35(Suppl 1): 5−10.

[6] 胡夏闽, 薛伟, 曹雪娇. 钢−混凝土组合梁挠度计算的附加曲率法[J]. 建筑结构学报, 2010(增1): 385−389. HU Xiamin, XUE Wei, CAO Xuejiao. The additional curvature method for calculating deflection of composite steel-concrete beams[J]. Journal of Building Structures, 2010(Suppl 1): 385−389.

[7] 徐荣桥, 陈德权. 组合梁挠度计算的改进折减刚度法[J]. 工程力学, 2013, 30(2): 285−291. XU Rongqiao, CHEN Dequan. Modified reduced stiffness method for calculating the deflection of composite beams[J]. Engineering Mechanics, 2013, 30(2): 285−291.

[8] 樊健生, 施正捷, 芶双科, 等. 钢-ECC组合梁负弯矩区受弯性能试验研究[J]. 土木工程学报, 2017, 50(4): 68−76. FAN Jiansheng, SHI Zhengjie, GOU Shuangke, et al. Experimental research on negative bending behavior of steel-ECC composite beams[J]. China Civil Engineering Journal, 2017, 50(4): 68−76.

[9] 秦凯, 胡夏闽, 江雨辰, 等. 部分外包混凝土组合梁负弯矩区翼缘板裂缝试验研究[J]. 建筑钢结构进展, 2018, 20(5): 31−38. QIN Kai, HU Xiaming, JIANG Yuchen, et al. Experimental study on slab cracks in the negative moment regions of partially concrete encased composite beams[J]. Progress in Steel Building Structures, 2018, 20(5): 31−38.

[10] 冯康平, 曹晓亮, 张彦玲. 钢混组合梁负弯扭作用下的受力性能试验研究[J]. 广西大学学报(自然科学版), 2017, 42(4): 1299−1306. FENG Kangping, CAO Xiaoliang, ZHANG Yanling. Experimental research on mechanical behavior of steel-concrete composite beams under combined negative bending moment and torque[J]. Journal of Guangxi University (Natural Science Edition), 2017, 42(4): 1299− 1306.

[11] 易海波. 钢−混凝土组合梁翼板有效宽度的试验与分析[D]. 长沙: 湖南大学, 2005. YI Haibo. The experiment and analysis of the effective width value in steel-concrete composite beams[D]. Changsha: Hunan University, 2005.

[12] Loh H Y, Uy B, Bradford M A. The effects of partial shear connection in the hogging moment regions of composite beams Part I-Experimental study[J]. Journal of Constructional Steel Research, 2004, 60(12): 897−919.

[13] Vasdravellis G, Uy B, Kirkland B, et al. Behaviour and design of composite beams subjected to negative bending and compression[J]. Journal of Constructional Steel Research, 2012, 79(12): 34−47.

[14] Lin W, Yoda T, Taniguchi N. Mechanical performance of steel-concrete composite beams subjected to a hogging moment[J]. Journal of Structural Engineering, 2014, 140(1): 04013031

[15] BS5950-3.1: British standard structural use of steelwork in building. Part 3: Design In Composite Construction[S]. London: British Standards Institution, 1990.

[16] AISC-LRFD. Load and resistance factor design specification for structural steel buildings[S]. Chicago, US: 2005.

[17] 聂建国, 樊健生. 组合梁在负弯矩作用下的刚度分析[J]. 工程力学, 2002, 19(4): 33−36. NIE Jianguo, FAN Jiansheng. Analysis of composite beam stiffness under negative bending[J]. Engineering Mechanics, 2002, 19(4): 33−36.

[18] DING Faxing, YIN Guoan, WANG Haibo, et al. Static behavior of stud connectors in bidirection push-off tests[J]. Thin-Walled Structures, 2017, 120(11): 307−318.

[19] LIU Jing, DING Faxing, LIU Xuemei, et al. Flexural capacity of steel-concrete composite beam under hogging moment[J]. Advances in Civil Engineering. 2019, Article ID 3453274: 1−13.

[20] GB 50010—2010, 混凝土结构设计规范[S]. GB 50010—2010, Code for design of concrete structures[S].

Flexural stiffness of steel-concrete composite beam under negative moment

LIU Jing1, 2, DING Faxing2, JIANG Lizhong2, FU Lei2, HUANG Yan1

(1. School of Civil Engineering, Hunan City University, Yiyang 413000, China; 2. School of Civil Engineering, Central South University, Changsha 410075, China)

This paper investigated the flexural stiffness of steel-concrete composite I-beam under negative bending moment through combined experimental and finite element (FE) modeling.13 composite beams were included into the experiments and parameters including shear connection degree, transverse and longitudinal reinforcement ratio were also considered and investigated. ABAQUS was employed to establish FE models to simulate the behavior of composite beams. The influences of a few key parameters, such as the shear connection degree, stud arrangement, stud diameter, loading position, longitudinal reinforcement ratio and beam length on flexural stiffness were discussed. The results show that degree of shear connection affect flexural stiffness most, reinforcement ratio has some influence, remaining arguments have little effect. In addition, Chinese code, the formula by other scholar were used to estimate the flexural stiffness and also compared with the simulation results. The results indicate that the modified formula proposed in this article may provide a better estimation in comparison to other methods.

steel-concrete composite beam; flexural stiffness; finite element; degree of shear connection

TU398

A

1672 − 7029(2019)09− 2281 − 09

10.19713/j.cnki.43−1423/u.2019.09.020

2018−10−28

国家重点研究计划项目(2017YFC0703404)；湖南省自然科学基金项目(2018JJ3021，2019JJ20029)；中国博士后科学基金项目(2018M 632990)；湖南省教育厅科学研究优秀青年项目(18B438)

丁发兴(1979−)，男，浙江瑞安人，教授，博士，从事钢−混凝土组合结构研究；E−mail：dinfaxin@csu.edu.cn

(编辑 涂鹏)