水下椭圆形隧道稳定渗流的近似解

贺志军，莫海强，邹金锋，李超

水下椭圆形隧道稳定渗流的近似解

贺志军1，莫海强2，邹金锋2，李超2

(1. 中南大学 交通运输工程学院，湖南 长沙 410075；2. 中南大学 土木工程学院，湖南 长沙 410075)

利用复变函数数值保角映射结合最优化技术，推导在完全饱和、均匀和各向同性半无限含水层中水平地下椭圆形隧道二维稳定渗流的近似解析解。在考虑水下隧道周边恒定水头和水压边界条件下，通过近似解可以计算隧道周围水头和孔隙水压的分布。此外，对基于本文求出的近似解与有限差分FLAC3D分别计算在恒定水压边界条件下隧道周围的孔隙水压作对比。研究结果表明：近似解求得隧道周围孔隙水压与有限差分数值模拟的解吻合度高，对于水下椭圆形隧道初步设计来预测隧道周围水压分布是有意义的。

数值保角映射；最优化技术；稳定渗流；椭圆形隧道；近似解析解；水下隧道

隧道作为一种重要的交通基础设施，广泛应用于工程建设中。对于水下隧道，由于处于高水压且水源充足，其渗水问题远比陆地隧道严重，且渗流对水下隧道的设计和建设影响较大。对于水下非圆形隧道，其隧道周边的渗流场会受到隧道形状影响。在隧道形状研究方面，范广勤等[1]应用六角形去逼近天幕线拱形直墙洞室，适用性较差；吕爱钟等[2−3]采用最优化技术确定任意截面形状巷道的映射函数，同时给出非圆整体式支护保角映射成圆环域，克服了以往按单连通域方法计算双连通域问题的缺陷；陆文超等[4]在Verruijt[5]成果的基础上，利用复变函数法研究了地面荷载下浅埋隧道围岩的应力问题。在隧道渗流场研究方面，Harr等[6−8]根据镜像法获得隧道周围地层的孔隙水压力分布；Joo等[9]研究了衬砌外水头和隧道涌水量的关系；王秀英等[10]获得山区高水位隧道注浆圈外水头的表达式；Tani[11]提出了基于Mobius变换和傅里叶级数的渗流方程；Kolymbas等[12−13]用保角变换获得不同边界条件对应的解析解；HUANGFU等[14]研究一种圆形水下隧道在恒定水头和隧道周边恒定水压边界条件下的稳定渗流场的解析解，并用FLAC3D进行了验证。综上所述，对于隧道渗流场的研究，大部分学者侧重于对圆形隧道的分析，对于许多有工程意义的孔口问题，不能像圆孔那样仅由有限项组成的准确的映射函数，本文运用最优化技术复合形法，经过多次保角变换，基于HUANGFU等[14]研究扩展，在像平面中根据达西定律，求解拉普拉斯方程得出水下任意孔形隧道稳定渗流的近似解，并用FLAC3D验证解的正确性。

1 基本假设

为了求解这个问题，做出如下假设：1) 地表水平，隧道横截面为椭圆形，位于含水层中；2) 渗流为无旋稳定；3) 流体不可压缩；4) 隧道周边地层为各向同性的多孔连续介质。建立模型如图1所示。隧道中心距地面的深度用表示，椭圆隧道长轴和短轴分别用和表示，地面以上的水深为h。

2 保角变换

根据达西定律和质量守恒定律，隧道周边二维稳定渗流遵循拉普拉斯方程：

其中：

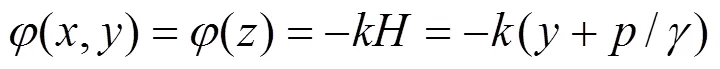
图1 水下隧道的几何模型

Fig. 1 Model of seepage around underwater tunnel

保角变换的变换函数一般分为解析法和数值方法。对于解析法，变换函数只有在极少数的情况下能用初等函数表示，所以很多情况下只能指出变换函数的存在，而不能完全解出变换函数，由于在实际工程问题的复杂性，很多情况下必须利用数值方法求解满足给定条件下的保角变换问题。由于本文讨论的是半空间下椭圆孔问题，其变换函数不能直接用初等函数表示，所以只能用数值方法构造一个函数来逼近变换函数。根据对称性，取一半结构分析，将原平面(平面)渗流区域映射到像平面(平面)的矩形区域分3步，变换模型如图2所示，其中相邻的连线表示各个平面内所对应的边界，P，P分别指边和边的势函数，但是其中(b)变换到(c)时利用了数值保角变换，变换函数存在一定的误差。

2.1 第1次变换

Verruijt[5]运用分式线性变换，把原平面含圆形孔洞的半平面体映射成像平面单位圆环域，对于任意孔形的半平面只能将外表面也就是地表边界变换成单位圆，隧道边界变换为一个非圆图形。分式线性变换公式如下；

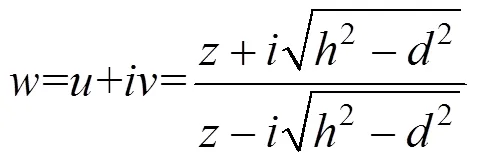
式中：z=x+iy，为渗流区域中的点集；d为隧道中心的在y方向的高度的一半；h为隧道高度中心距地面的深度。通过输入隧道边界点位，可以明确的观察到变换后内边界非圆图形，如图2(a)和2(b)。

2.2 第2次变换

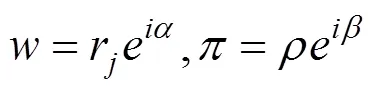
式中：为正实数；C一般为复数，因为对称性，所以C必为实数。

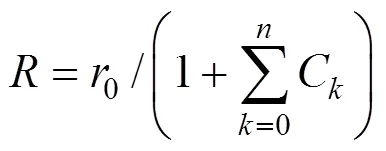
目标函数取：

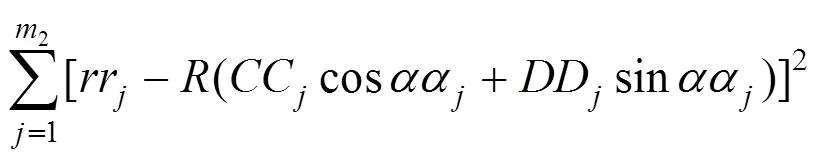
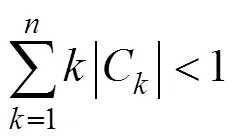
2.3 第3次变换

将半圆环区域单叶保形变换为矩形区域，如图2(c)~2(d)，变换函数为

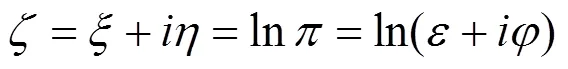
通过3次保角变换，可以将半无限空间下椭圆孔问题近似转化为矩形问题。

由于第2部数值保角变换函数精度随着C值个数的增加，不过也导致式(4)的逆函数非常复杂，但是保角变换函数是单叶函数，即不同域中的点一一对应，所以通过式(3)和式(4)得：

式(8)为隐函数方程，可以求出平面与平面之间的关系，再将式(8)代入式(7)就可以得到平面变换为平面的变换函数，即：

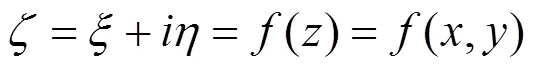
3 问题的求解

3.1 考虑隧道周边恒定水头

返回原平面(平面)：

将式(2)代入上式(12)，可得

3.2 考虑隧道周边恒定水压

假设渗流区域流体是不可压缩且是各向同性，均匀的。可得：

返回原平面，上式为：

然而上述压力解推导是在忽略重力的影响下。实际上压力跟容重和深度有关，因此对压力进行修正：

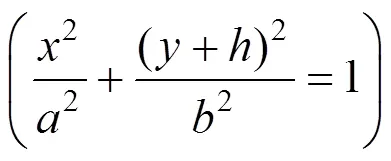
将式(19)代入(18)得：

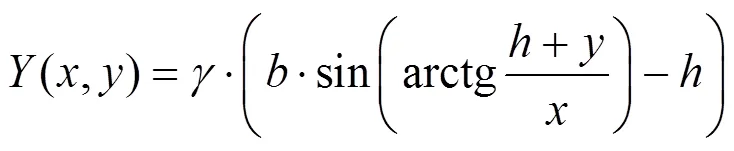
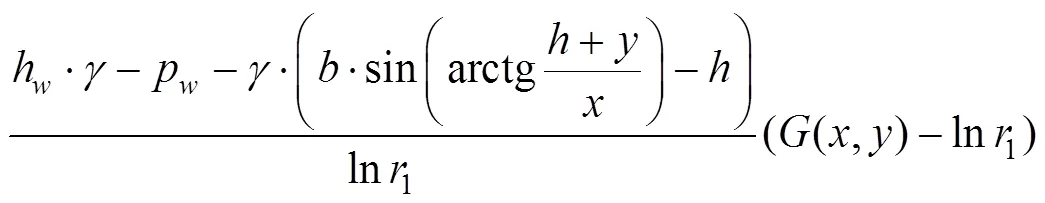
4 近似解验证

通过第1次变换，将地表映射为单位圆，内边界为非圆图形，变换函数如下：

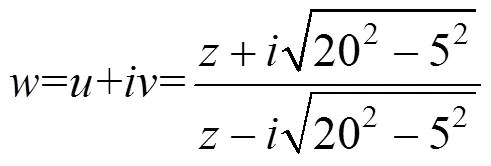
第2次变换，分别在内边界和外边界上取一定坐标点，通过上述以劳伦级数为基础的复合形法求出水下椭圆隧道的数值保角变换函数，此时式(4)表示如下：

当=6时：1=6.084 5

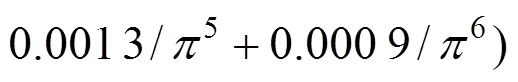
将所求变换函数返回原平面的映射图像和原模型图像相比较，黑线为原图形，蓝色虚线表示映射图形，如图3。在椭圆隧道边界最大误差为0.233 m，在地表边界(沿轴方向80 m内)最大误差为0.188 m。整体映射误差很小，符合工程要求。

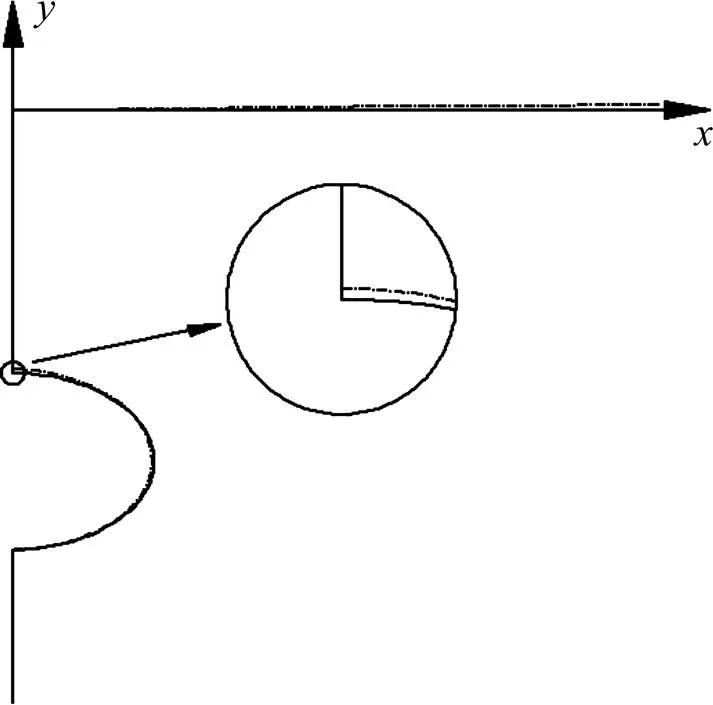
图3 原图形与映射图形比较

将式(22)和(23)代入式(8)中就可以得到隐函数方程，然后可以确定通过保角变换后，原、像平面点位之间的对应关系，最后通过上节所述的方法求得隧道周边的水压值。

利用FLAC3D建立此算例下的隧道模型，隧道埋深20 m，为了消除边界条件影响，故在数值模型方面，取计算宽度共160 m，计算深度为100 m。根据假设，地下水补给充足，所以数值模型边界处水压恒定且沿深度分布。采用单步稳定渗流模式，计算其孔隙水压场，因为各向同性，取渗透系数=10−5m/s，孔隙率为0.5，流体体积模量为=2 GPa，流体密度为=103kg/m3，数值计算模型见 图4。

图4 数值模型

然后由本文所推导的近似解求得水下椭圆隧道周围孔隙水压分布的计算结果，并和有限差分FLAC3D计算作比较，如图5~6所示。

图5 比较隧道周边水压分布FLAD3D(左边)与本文解(右边)

图6 本文解与FLAC3D解相比较

在图5中，从2种方法得到的孔隙水压的等压线可知，其中越靠近隧道，两者结果几乎相同，但是离隧道越远，其结果差值慢慢变大。图6中(a)图表示地表以下隧道中心线以上的水压分布，即(d)中的(1-2)，除了因为数值保角变换误差使映射椭圆边界向上偏移0.233 m，导致近似解只能在地表下14.767 m时才能计算其压力，在大约地表下14 m上产生的误差最大，近似解计算值为23.49 kPa，数值解为29.34 kPa，误差为19.9%，但是随着高度增加，变换函数更加精确，近似解与数值解误差大大减小，在地表以下12 m范围内，最大孔隙水压出现在地表，孔隙水压值为302.25 kPa，与数值计算值300 kPa，误差为0.75%，最大误差为1.825%，出现在大约地表下8 m处，近似解计算值为170.07 kPa，数值解为167.03 kPa，本文解和有限差分解基本吻合。(b)图表示隧道中心线以下的水压分布，即(d)中的(3-4)，其中最大误差是靠近在隧道附近，在地表以下26 m附近，近似解得36.72 kPa，数值解为39.73 kPa，误差为7.56%，随着深度增加，孔隙水压基数变大，其误差将越来越小。(c)图表示地表以下20 m，过隧道中心水平线上的水压分布，即(d)中的(5-6)，在距中心50 m范围之内，最大误差为6.37%，超过50 m外，两者结果逐渐偏离。从整体上看，误差都比较小，说明在隧道周围本文解与FLAC3D解几乎匹配，验证本文所推导公式的正确性和可靠性。

5 结论

1) 运用劳伦级数为基础的的复合形法求出水下椭圆隧道形状的变换函数，由变换函数为单叶函数说明本文解收敛，当变换函数足够精确时，此时推导的解可以视为解析解。

2) 推导了水下椭圆隧道渗流场的近似解析解，并利用解出的隧道周围水压分布与FLAC3D解相比较，匹配度很高，证明本文解的正确性。所以在给定的假设条件下，本文解对于水下任意孔形隧道初步设计预测隧道周边水压分布具有一定意义。

[1] 范广勤, 汤澄波. 应用三个绝对收敛级数相乘法解非圆形洞室的外域映射函数[J]. 岩石力学与工程学报, 1993, 12(3): 255−255. FAN Guangqin, TANG Chengbo. Determination of the mapping function for the exterior domain of a non-circular opening by means of the multiplication of three absolutely convergent series[J]. Chinese Journal of Rock Mechanics and Engineering, 1993, 12(3): 255−255.

[2] 吕爱钟, 张路青. 地下隧洞力学分析的复变函数方法[M]. 北京: 科学出版社, 2007. LU Aizhong, ZHANG Luqing. Complex variable function method for mechanics analysis of underground tunnels[M]. Beijing: Science Press, 2007.

[3] 吕爱钟. 非圆形硐室封闭整体式支护映射函数确定的新方法[J]. 岩土工程学报, 1995, 17(4): 38−44. LU Aizhong. A new method of determination of the mapping function for a non-circle tunnel with full support [J].Geotechnical Engineering, 1995, 17(4): 38−44.

[4] 陆文超, 仲政, 王旭. 浅埋隧道围岩应力场的解析解[J]. 力学季刊, 2003, 24(1): 50−54. LU Wenchao, ZHONG Zheng, WANG Xu. Analytical solution for stress field in surrounding rocks of shallow tunnel[J]. Chinese Quarterly of Mechanics, 2003, 24(1): 50−54.

[5] Verruijt A. A complex variable solution for a deforming circular tunnel in an elastic half-plane[J]. International Journal for Numerical and Analytical Methods in Geomechanics, 2015, 21(2): 77−89.

[6] Harr M E. Groundwater and seepage[M]. McGraw-Hill, 1962.

[7] Fernandez G, Alvarez J T A. Seepage-induced effective stresses and water pressures around pressure tunnels[J]. Journal of Geotechnical Engineering, 1994, 120(1): 108− 128.

[8] LEI S. An analytical solution for steady flow into a tunnel[J]. Ground Water, 1999, 37(1): 23−26.

[9] Joo E J, Shin J H. Relationship between water pressure and inflow rate in underwater tunnels and buried pipes[J]. Geotechnique, 2014, 64(3): 226.

[10] 王秀英, 王梦恕, 张弥. 计算隧道排水量及衬砌外水压力的一种简化方法[J]. 北京交通大学学报, 2004, 28(1): 8−10. WANG Xiuying, WANG Mengshu, ZHANG Mi. A simple method to calculate tunnel discharge and external water pressure on lining[J]. Journal of Northern Jiaotong University, 2004, 28(1): 8−10.

[11] Tani M E. Circular tunnel in a semi-infinite aquifer[J]. Tunnelling and Underground Space Technology Incorporating Trenchless Technology Research, 2003, 18(1): 49−55.

[12] Kolymbas D, Wagner P. Groundwater ingress to tunnels– The exact analytical solution[J]. Tunnelling and Underground Space Technology, 2007, 22(1): 23−27.

[13] Park K H, Owatsirwong A, Lee J G. Analytical solution for steady-state groundwater inflow into a drained circular tunnel in a semi-infinite aquifer: a revisit[J]. Tunnelling and Underground Space Technology, 2008, 23(2): 206−209.

[14] HUANGFU Ming, WANG Mengshu, TAN Zongsheng. Analytical solutions for steady seepage into an underwater circular tunnel[J]. Tunnelling and Underground Space Technology, 2010, 25(4): 391−396.

[15] 刘惟信. 机械最优化设计[M]. 北京: 清华大学出版社, 1997.LIU Weixin. Mechanical optimization design[M].Beijing: Tsinghua University Press, 1997.

Approximate analytical solutions for steady seepage into an underwater elliptical tunnel

HE Zhijun1, MO Haiqiang2, ZOU Jinfeng2, LI Chao2

(1. School of Traffic and Transportation Engineering, Central South University, Changsha 410075, China; 2. School of Civil Engineering, Central South University, Changsha 410075, China)

Based on the numerical conformal mapping of complex variable methods and the optimization techniques, the approximate analytical solutions were derived for two-dimensional, steady ground water flow into a horizontal elliptical tunnel in a fully saturated, homogeneous, isotropic, and semi-infinite aquifer. Under the conditions of constant hydraulic head and constant water pressure boundary surrounding the underwater tunnel, the distribution of hydraulic head and the pore water pressure around the tunnel can be calculated by the approximate analytical solutions. Moreover, a comparison of the approximate solutions and the finite difference FLAC3Dwas made for calculating the pore water pressure around the tunnel under constant water pressure boundary. The result shows that the solutions match well for points around the tunnel and it appears to be useful for a preliminary design of underwater tunnels to predict the water pressure distribution around the tunnel.

numerical conformal mapping; optimization techniques; steady seepage; elliptical tunnel; the approximate analytical solutions; underwater tunnel

U45

A

1672 − 7029(2019)09− 2265 − 07

10.19713/j.cnki.43−1423/u.2019.09.018

2018−11−17

国家重大专项项目(2017YFB1201204)

邹金锋(1978−)，男，河南新县人，教授，从事岩土与地下工程研究；E−mail：zoujinfeng_csu@163.com

(编辑 涂鹏)