不同激励下橡胶混凝土轨道板对轨道交通箱型梁减振效果分析

刘林芽，王璇，秦佳良

不同激励下橡胶混凝土轨道板对轨道交通箱型梁减振效果分析

刘林芽，王璇，秦佳良

(华东交通大学 铁路环境振动与噪声教育部工程研究中心，江西 南昌 330013)

为研究不同激励下橡胶混凝土轨道板对轨道交通箱型梁的减振效果，基于UM和ANSYS相结合的联合仿真方法，建立车-轨-桥耦合模型获取轮轨垂向力，考虑橡胶混凝土轨道板和普通轨道板2种轨道板，分别计算列车荷载和移动常力作用下箱型梁的振动响应，并通过插入损失分析评价不同激励下橡胶混凝土轨道板的减振效果。研究结果表明：不同激励作用下，橡胶混凝土轨道板都对轨道交通箱型梁结构有较好的减振效果。与列车荷载相比，移动常力会高估橡胶混凝土轨道板的减振效果。在用插入损失评价减振效果时应尽可能选择与现场条件符合的激励才能得到实际的减振效果。

橡胶混凝土轨道板；箱型梁；减振效果；插入损失

随着城市轨道交通不断深入人们的生活，车辆运行所带来的环境振动问题也愈加突出[1]。在轨道交通的减振方式中，除了常用的降低刚度的方法外，还可以通过增加阻尼、吸收振动能量的方法来达到减振目的。基于此，提出利用橡胶混凝土来制作一种新的减振措施——橡胶混凝土轨道板。对于橡胶混凝土，国内外学者已经做了一些研究。Khatih等[2]用共振法测量了橡胶混凝土的弹性模量，得出橡胶混凝土弹性模量低有助于改善混凝土工程性能的结论。Coverntry等[3]研究表明橡胶混凝土的韧性和抗冲击性能相比于普通混凝土有明显改善，在受到冲击荷载时，橡胶的掺入可有效防止混凝土破坏。袁勇等[4-5]的试验结果显示随着橡胶掺量的增加，橡胶混凝土阻尼比不断增大，而弹性模量和基频随橡胶掺量的增加而降低，说明橡胶混凝土具有较好的吸振能力。WONG等[6]就强烈建议将这种高阻尼的混凝土用于结构或构件的振动控制，为进一步探讨其在轨道交通减振降噪领域的应用前景，首先需对其减振效果进行研究。目前，工程技术中常采用插入损失来评价减振效果[7]，但插入损失并非结构的固有属性，其值与所受激励有关。因此对于同一减振措施，所受激励不同其插入损失也会有差异。为研究不同激励下橡胶混凝土轨道板对轨道交通箱型梁的减振效果，考虑2种轨道板建立了箱型梁有限元模型，基于UM与ANSYS相结合的联合仿真方法，建立车−轨−桥系统耦合模型获取轮轨垂向力，施加轮轨垂向力和移动常力2种激励，计算分析列车荷载和移动常力作用下橡胶混凝土轨道板对箱型梁的减振效果。

1 模型建立及计算参数

1.1 轨道交通箱型梁有限元模型

采用常见的轨道交通高架箱型梁作为研究对象，其标准跨径32 m，梁高2.8 m，宽为12.97 m，顶板厚度为0.34 m，底板厚度为0.3 m，腹板厚度为0.468 m，翼缘厚度为0.2 m，支座设在距梁端0.32 m处，箱型梁截面如图1所示。

在箱型梁有限元模型中，采用梁单元模拟钢轨；采用弹簧阻尼单元模拟扣件系统；采用实体单元模拟轨道板及CA砂浆；采用赋予实际厚度的板壳单元模拟箱梁结构，有限元模型如图2所示。主要结构参数见表1，表1中橡胶混凝土轨道板的各项参数均为实验测试所得。

单位：mm

表1 主要结构参数表

1.2 车−轨−桥系统耦合模型

基于UM与ANSYS相结合的联合仿真方法，建立车−轨−桥系统耦合模型。列车模型的各项参数参照实际地铁B型车选取，通过多体动力学软件UM建立。其中单节列车可认为由1个车体、2个转向架及4个轮对组成，每节车辆考虑了伸缩、横移、沉浮、摇头、侧滚、点头6个自由度，共考虑42个自由度。由于我国轨道不平顺谱和德国低干扰谱比较接近[8]，在UM中采用德国低干扰谱作为激励谱。列车各项参数见表2。

图2 箱型梁有限元模型

表2 地铁B型车参数表

将箱型梁有限元模型作为柔性体导入UM软件，基于UM柔性轨道模块，可以把桥梁柔性体与轨道系统通过2排(左右轨)有间隔的力元相连，从而实现车−轨−桥系统的耦合。车−轨−桥系统耦合模型如图3所示。

1.3 2种激励的获取

本文采用1节地铁B型车模拟加载，计算速度设为80 km/h，通过车−轨−桥耦合模型获取轮轨垂向力如图4所示，并取轴重的一半(70 kN)作为移动常力。将列车实际运行过程简化为8个随时间移动的集中力荷载，将这些移动的集中力分别加载[9-10]在橡胶混凝土轨道板−箱型梁有限元模型和普通轨道板−箱型梁有限元模型上，加载步长均取为0.002 323 8 s。

图3 车-轨-桥系统耦合模型

图4 轮轨垂向力时程曲线

从图4可以看出，本文计算得到的轮轨垂向力在70 kN附近波动，这是由于本文建立的地铁B型车轴重为14 t，文献[11]在德国低干扰谱激励下得到的轮轨垂向力也符合这一规律，且轮轨力时程曲线吻合较好，这表明本文模型计算得到的轮轨力结果良好，可用于下文的动力学计算。

2 不同激励下减振效果对比分析

2.1 列车荷载作用下箱型梁振动响应

将计算出来的轮轨垂向力分别加载到橡胶混凝土轨道板−箱型梁和普通轨道板−箱型梁有限元模型上，对2者进行瞬态动力分析，其基本运动方 程为：

为了便于比较2种激励下的减振效果，均选取如图5所示的箱型梁跨中截面输出点，其中1~4号点分别代表顶板中心、底板中心、腹板中心和右翼缘的端点。通过瞬态动力分析得出各输出点的时域响应；再通过傅里叶变换对各输出点响应进行频谱分析，得到如图6~9所示的各输出点的加速度振级曲线。

图5 箱型梁跨中截面输出点

表3 本文计算结果与文献对比

图6 列车荷载作用下顶板垂向加速度振级

图7 列车荷载作用下底板垂向加速度振级

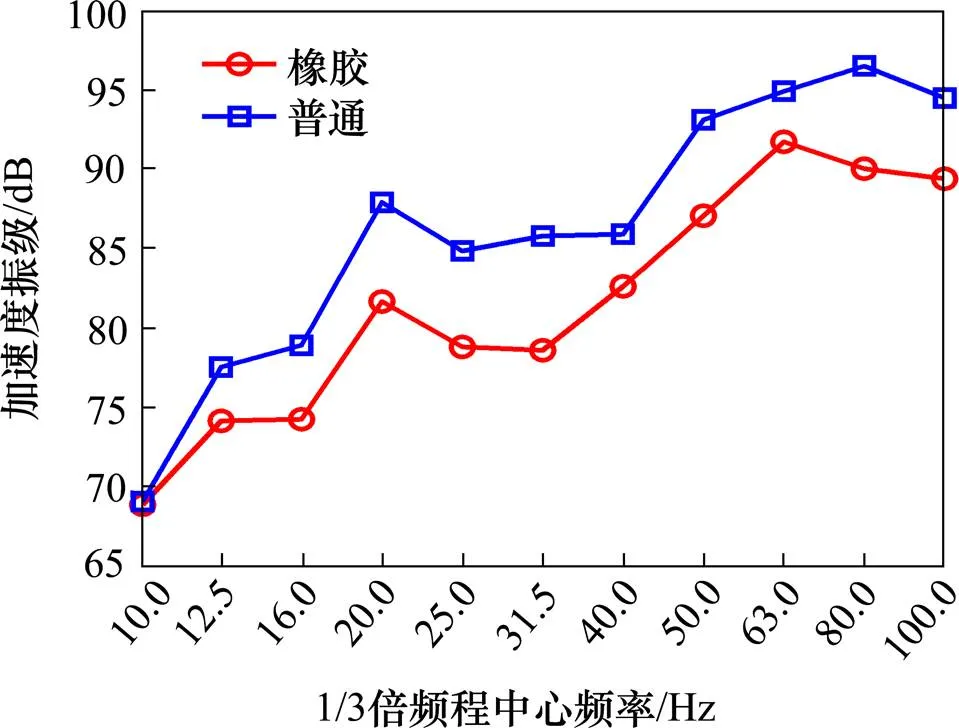
图8 列车荷载作用下腹板横向加速度振级

图9 列车荷载作用下翼缘垂向加速度振级

由表3可知：本文的计算结果与文献[12]中实测结果相比，箱梁板件加速度振级峰值偏大，这可能是由于列车实际运行速度一般低于本文计算速度80 km/h导致，但加速度振级峰值频率吻合较好，箱梁结构振动的主要峰值频率均为50~80 Hz附近，说明本文建立的模型是可靠的。

由图6~9可知：列车荷载作用下，2种轨道板下各输出点的频谱变化规律基本上一致，但橡胶混凝土轨道板下箱型梁的加速度振级均比普通轨道板下的小，其最大振级差在顶板63 Hz处达到15.8 dB，说明橡胶混凝土轨道板对箱型梁有较好的减振效果。

2.2 移动常力作用下箱型梁振动响应

将移动常力分别加载到橡胶混凝土轨道板−箱型梁和普通轨道板−箱型梁有限元模型上，得到如图10~13所示的各输出点的加速度振级曲线。

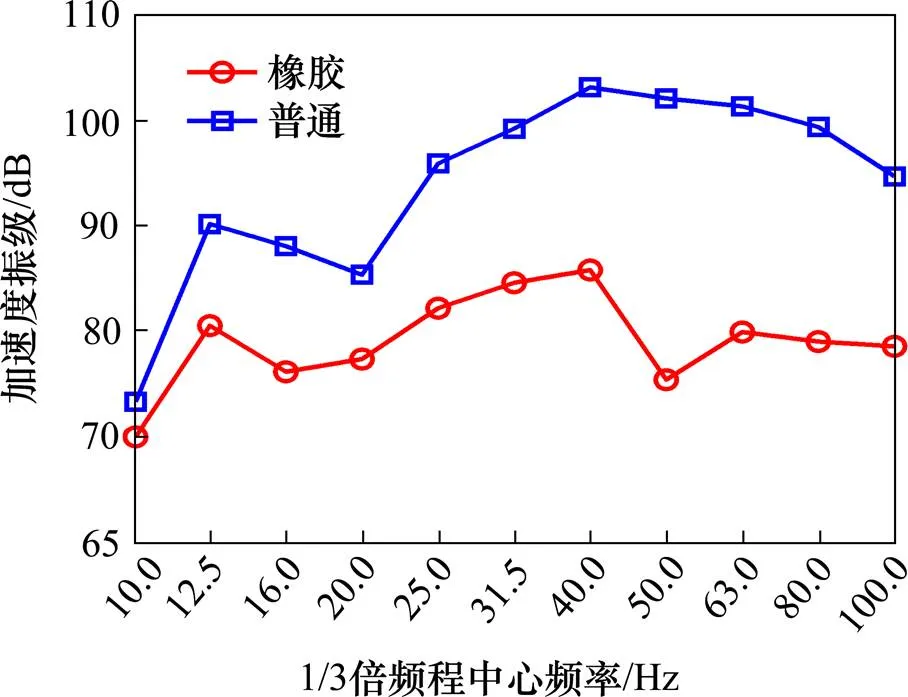
图10 移动常力作用下顶板垂向加速度振级

图11 移动常力作用下底板垂向加速度振级

图12 移动常力作用下腹板横向加速度振级

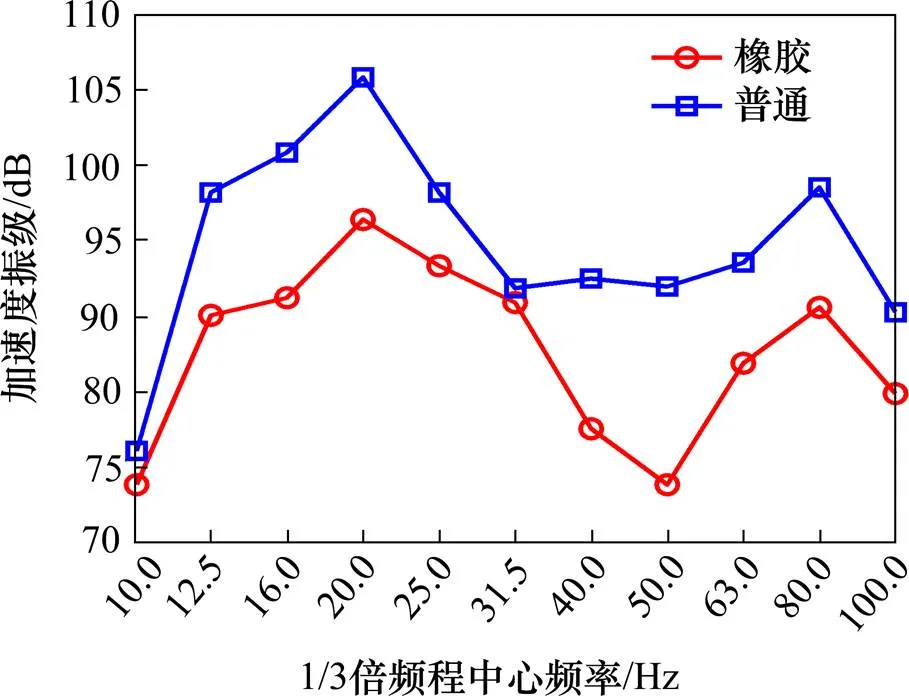
图13 移动常力作用下翼缘垂向加速度振级

由图10~13结合图6~9可知：移动常力荷载作用下的各输出点振动特性与列车荷载作用下的相似，而橡胶混凝土轨道板下箱型梁的加速度振级均比普通轨道板下的小，说明2种激励作用下橡胶混凝土轨道板都对箱型梁有较好的减振效果。

2.3 2种不同激励作用下插入损失对比分析

本文采用插入损失L来评价不同激励作用下橡胶混凝土轨道板的减振效果，其表达式为：

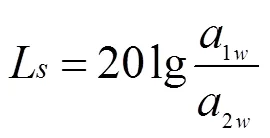
式中：a1w和a2w为普通轨道板和橡胶混凝土轨道板下各输出点的频域计权加速度有效值。当Ls>0时，说明减振措施起到了减振效果，且Ls越大减振效果越好；当Ls<0时说明减振措施没有起到减振效果反而放大了振动。对各输出点振动响应经上述公式计算得到插入损失如图14~17所示。

图15 2种激励下底板插入损失

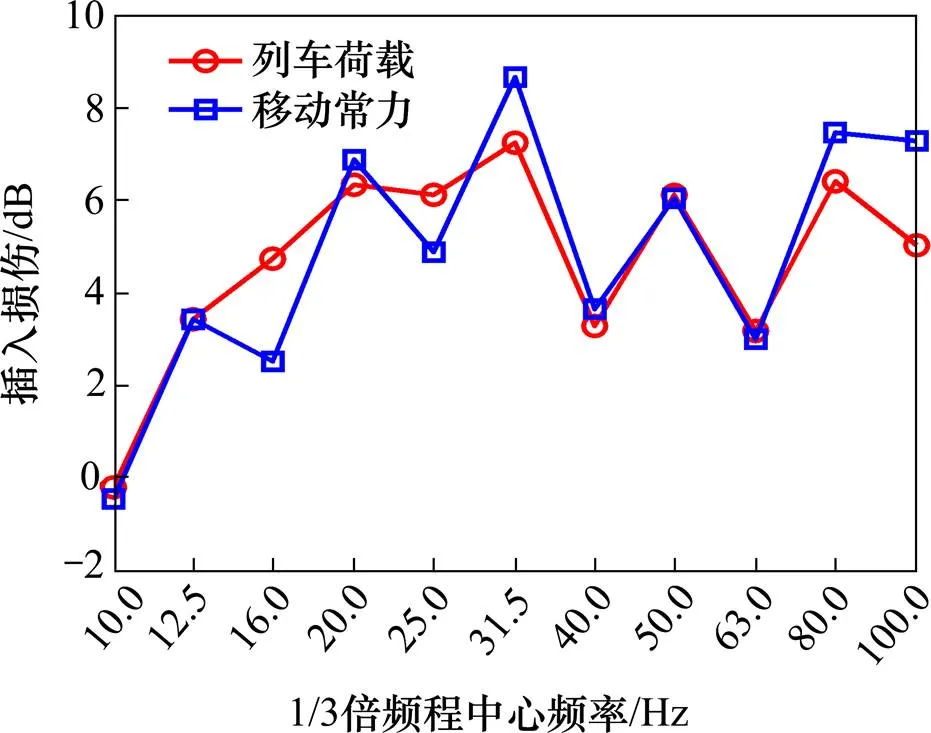
图16 2种激励下腹板插入损失

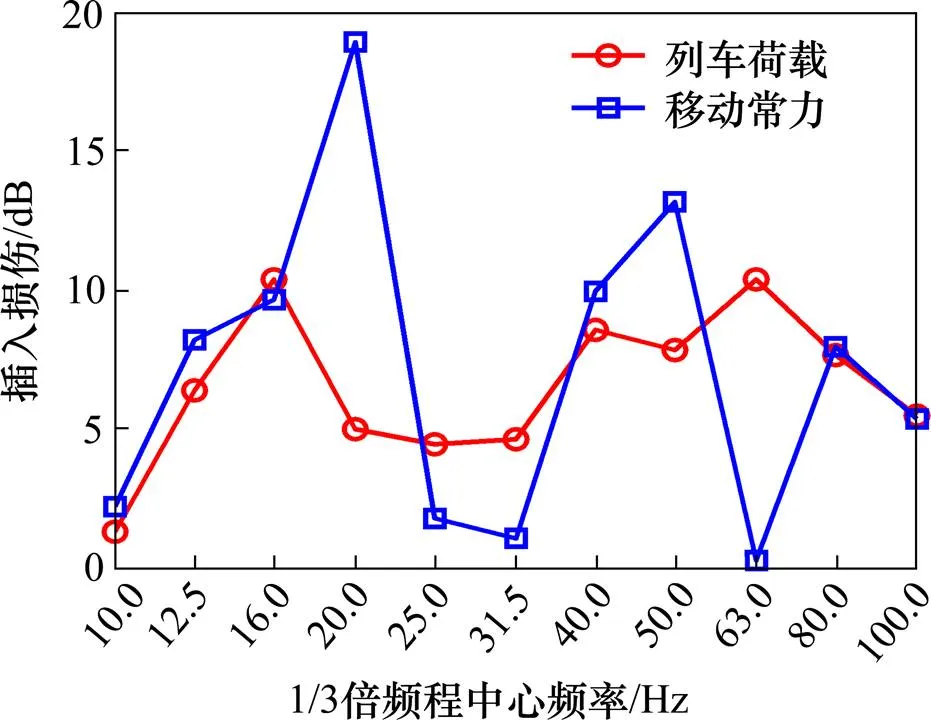
图17 2种激励下翼缘插入损失

从各输出点的插入损失图像可以看出：

1) 2种不同激励作用下，各输出点的插入损失曲线在10~100 Hz全频段内总体上均处于正值区间，这表明2种不同激励作用下橡胶混凝土轨道板对轨道交通箱型梁结构都有较好的减振效果。2) 移动常力作用下计算得到的插入损失在10~100 Hz的绝大部分频段内大于列车荷载作用下计算得到的插入损失，即移动常力与列车荷载相比会高估橡胶混凝土轨道板的减振效果。

3 结论

1) 2种不同激励作用下，橡胶混凝土轨道板下各输出点的加速度振级均比普通轨道板下的小，说明2种激励下，橡胶混凝土轨道板都对轨道交通箱型梁有较好的减振效果。

2) 移动常力作用下计算得到的插入损失在绝大部分频段内大于列车荷载作用下得到的插入损失，即移动常力与列车荷载相比会高估橡胶混凝土轨道板的减振效果。

3) 插入损失作为减振措施常用的评价指标，其值与所受激励有关，不同激励作用下，即使同一减振措施其插入损失也会有差异，因此在评价减振效果时应尽可能选择与现场条件符合的激励才能得到减振措施实际的减振效果。

[1] 李林峰, 马蒙, 刘维宁, 等. 不同激励作用下钢弹簧浮置板轨道减振效果研究[J]. 工程力学, 2018, 35(增1): 253−258. LI Linfeng, MA Meng, LIU Weining, et al. Analysis for the vibration reduction characteristics of steel spring floating slab track under different types of excitation[J]. Engineering Mechanics, 2018, 35(Suppl 1): 253−258.

[2] Khatih Z K, Bayomy F M. Rubberized portland cement concrete[J]. Journal of Materials in Civil Engineering, 1999, 13(2): 206−213.

[3] Coventry K, Richardson A, Diaz E. Impact resistance of concrete-using slit rubber fromtyres[J]. Journal of Harbin Institute of Technology, 2015, 21(4): 43−46.

[4] 袁勇, 郑磊. 橡胶混凝土动力性能试验研究[J]. 同济大学学报(自然科学版), 2008(9): 1186−1190. YUAN Yong, ZHENG Lei. Experimental study on dynamic properties of rubberized concrete[J]. Journal of Tongji University (Natural Science), 2008(9): 1186− 1190.

[5] 白文琦, 吕晶. 橡胶轻骨料混凝土阻尼性能试验[J]. 长安大学学报(自然科学版), 2018, 38(3): 26−33, 42. BAI Wenqi, LÜ Jin. Experimental on damping capacity of rubber lightweight aggregate concrete[J]. Journal of Chang’an University (Natural Science Edition), 2018, 38(3): 26−33, 42.

[6] WONG W C, FANG P, PAN J K. Polymer effects on the vibration damping behavior of cement[J]. Journal of Materals in Civil Engineering, 2003, 15(6): 554−556.

[7] 赵才友, 王平. 桥上无砟轨道橡胶减振垫减振性能试验研究[J]. 中国铁道科学, 2013, 34(4): 8−13. ZHAO Caiyou, WANG Ping. Experimental study on the vibration damping performance of rubber absorbers for ballastless tracks on viaduct[J]. China Railway Science, 2013, 34(4): 8−13.

[8] 刘林芽, 秦佳良, 曾峰. 轨道交通槽形梁局部振动及参数敏感性分析[J]. 铁道科学与工程学报, 2017, 14(11): 2363−2368. LIU Linya, QIN Jialiang, ZENG Feng. Research on local vibration and parameter sensitivity analysis of rail transit trough beam[J]. Journal of Railway Science and Engineering, 2017, 14(11): 2363−2368.

[9] CHEN Y J, JU S H, NI S H, et al. Prediction methodology for ground vibration induced by passing trains on bridge structures[J]. Journal of Sound and Vibration, 2007(302): 806−820.

[10] 高传伟, 唐雅茹, 余华. 基于移动荷载过桥的轨道交通桥梁振动研究[J]. 中国铁道科学, 2005, 26(2): 73−76.GAO Chuanwei, TANG Yaru, YU Hua. Study on the vibration of rail transit bridge based on moving load passing bridge[J]. China Railway Science, 2005, 26(2): 73−76.

[11] 崔召. 基于UM铁路桥梁车桥耦合振动响应分析[D].石家庄: 石家庄铁道大学, 2017. CUI Zhao. The analysis of vibration response of vehicle- bridge coupling system for railway bridges by UM[D]. Shijiazhuang: Shijiazhuang Tiedao University, 2017.

[12] 张迅, 李小珍, 刘全民, 等. 混凝土箱梁的结构噪声及其影响因素[J]. 西南交通大学学报, 2013, 48(3): 409−414. ZHANG Xun, LI Xiaozhen, LIU Quanmin, et al. Stucture-borne noise of concrete box-girder and its influence factors[J]. Journal of Southwest Jiaotong University, 2013, 48(3): 409−414.

Vibration reduction effect of rubber concrete track slab on box girder under different excitation

LIU Linya, WANG Xuan, QIN Jialiang

(Engineering Research Center, Ministry of Education, Railway Environmental Vibration and Noise, East China Jiaotong University, Nanchang 330013, China)

The purpose of vibration reduction was achieved by increasing the vibration energy absorbed by damping. In order to study the effect of rubber concrete track slab on the vibration reduction of rail transit box girder under different excitations, based on the combined simulation method of UM and ANSYS, a vehicle-rail-bridge coupling model was established to obtain the wheel-rail vertical force. Considering rubber concrete track slab and ordinary track slab, the train load and moving constant were calculated respectively. Vibration response of box girder under the action of force, and vibration reduction effect of rubber concrete track slab under different excitation was evaluated by insertion loss. The results show that: Under different excitations, rubber concrete track slabs have better vibration reduction effect on the box girder structure of rail transit. Compared with the train load, the mobile force will overestimate the damping effect of the rubber concrete track slab. When evaluating the effect of vibration reduction with insertion loss, we should choose the excitation which is in conformity with the site conditions as far as possible to obtain the actual effect of vibration reduction.

rubber concrete track slab; box girder; vibration reduction effect; insertion loss

U233；TB532

A

1672 − 7029(2019)09− 2168 − 07

10.19713/j.cnki.43−1423/u.2019.09.006

2018−11−16

国家自然科学基金资助项目(51578238，51968025)；江西省自然科学基金重点资助项目(20192ACBL2009)；江西省重点研发计划资助项目(20181BBE50013)

刘林芽(1973−)，男，江西樟树人，教授，从事铁路环境振动与噪声研究；E−mail：lly1949@163.com

(编辑 蒋学东)