考虑旧桥损伤的拼宽T梁桥荷载横向分布计算

邬晓光，黄成，李院军，殷悦

考虑旧桥损伤的拼宽T梁桥荷载横向分布计算

邬晓光，黄成，李院军，殷悦

(长安大学 公路学院，陕西 西安 710000)

现有关于拼宽桥梁荷载横向分布的研究多基于传统的横向分布计算方法，考虑旧桥损伤条件下的拼宽T梁桥荷载横向分布计算少有研究。为了提高拼宽T梁桥内力计算精度，考虑旧桥湿接缝损伤和主梁刚度损伤，并根据荷载试验与外观调查确定竖向剪力折减系数和主梁刚度分配系数，在传统刚接梁法理论的基础上推导出合理的计算方法。依托一座单侧拼宽的9梁式简支T梁桥，将计算得到的横向分布系数与传统刚接梁法、有限元数值法、荷载试验法计算结果进行比较。研究结果表明：计算拼宽T梁桥横向分布系数时，需考虑旧桥损伤的影响，本研究推导的计算方法能够较好地反映拼宽桥梁的实际受力；采用传统刚接梁法计算的拼宽桥梁横向分布系数结果偏于不安全。

桥梁工程；横向分布系数；刚接梁法；刚度损伤；湿接缝损伤

随着社会经济的发展，很多桥梁的宽度已经不能满足交通需求，需要对既有桥梁进行拓宽改造。荷载横向分布计算是桥梁拓宽设计中的重要内容。国内外学者在拼宽桥研究上多侧重于横向连接刚度大小对新旧桥梁整体受力的影响，并通过计算拼宽桥梁荷载横向分布来分析桥梁加宽之后的受力性能[1−9]。但是这些研究都是基于旧桥没有发生损伤情况下进行的探讨。事实上，大部分需要拼宽改造的桥梁都已经运营10 a甚至更长时间，受到当地环境及车辆荷载的影响，主梁刚度及湿接缝不可避免地出现损伤。传统的荷载横向分布计算方法都是默认桥梁处于完好状态，学者们采用的有限元模型也很少会考虑桥梁劣化的影响，从而不能真实反映拼宽桥梁的受力状态。何启龙等[10]考虑旧桥横向刚度劣化，对拼宽桥梁受力进行研究，发现拼宽桥梁在移动荷载的作用下，横向刚度的劣化会增加新旧桥梁的结构受力。所以在计算拼宽桥梁荷载横向分布时，不能忽略旧桥劣化对桥梁受力的影响。本文考虑旧桥湿接缝损伤和主梁刚度损伤，引入竖向剪力折减系数和主梁刚度分配系数，对传统刚接梁法进行适当修正。并以一座单侧拼宽的9梁式简支T梁桥为依托工程，建立考虑旧桥损伤的有限元模型，并结合荷载试验结果，对本文推导的计算方法进行验证，为今后拼宽桥梁设计及加固改造提供简便有效的计算方法。

1 考虑旧桥损伤的刚接梁法计算公式推导

1.1 基本假定

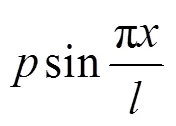
1.2 荷载分布

桥梁拼宽之前，旧桥已经服役多年。在汽车荷载、气候环境及材料老化等一系列作用下，旧桥的横向连接构造会出现不同程度损伤。T梁桥通过现浇湿接缝将各片主梁连接成整体。湿接缝损伤会导致桥面活载不能得到有效分配，使主梁处于不利的受力状态。传统的荷载横向分布计算方法假定桥梁处于完好的状态，然而对于拼宽桥梁这种将旧桥和新桥进行拼接的组合结构，如果仍然使用传统的计算方法忽视旧桥损伤，容易造成计算错误，不能反映桥梁的真实受力情况，对拼宽桥梁的受力与养护产生不利影响。

湿接缝发生损伤时，主梁之间传递的竖向剪力和横向弯矩发生变化。本文采用竖向剪力折减系数和横向弯矩折减系数来反映湿接缝损伤对竖向剪力和横向弯矩的变化。以5片T梁组成的桥梁为例，竖向剪力为原来的11，122，1233和12344，横向弯矩变为原来的15，126，1237和12348。

以求单位正弦荷载作用在1号梁上时的荷载横向分布为例，只要求得各片主梁间的竖向剪力就能得到各片梁的横向分布影响线竖标值，其值为：

式中：1i为1号主梁的荷载横向影响线在号梁处的竖标值(=1~5)。

从式(1)可以看出，只有确定折减系数和竖向剪力g，才能求出1号主梁在单位正弦荷载作用下的影响线竖标值。

1.3 竖向剪力折减系数

袁桂芳[11]通过测量桥梁在移动荷载作用下主梁之间最大位移差和主梁跨中最大挠度，对测量位移值采用协方差分析得到接缝损伤系数。

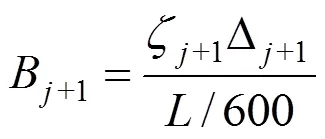
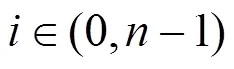
袁桂芳[11]研究认为，当接缝相对位移修正系数取0.5~0.6，主梁挠度修正系数取1~2.5时，接缝损伤判别准为：

将竖向剪力g乘以折减系数，以此表示竖向剪力的变化，则1−μ表示湿接缝损伤的程度，其取值范围为[0,1]。借用接缝损伤系数的概念，可以知道=1和=3是其临界值。认为当＜1时，1−μ=0，湿接缝完好，未发生损伤；当＞3时，1−μ=1，湿接缝破坏，完全失去其作用；当1＜＜3时，湿接缝发生部分损伤，1−通过插值确定。由此我们可以通过简单的荷载试验方法定量的确定竖向剪力折减系数。

1.4 正则方程的建立

竖向剪力g可以利用结构力学中的力法原理，并利用在和作用的截面左边和右边主梁的竖向位移和转角必须相等的变形协调条件，建立正则方程求解。力法基本体系如图1所示。

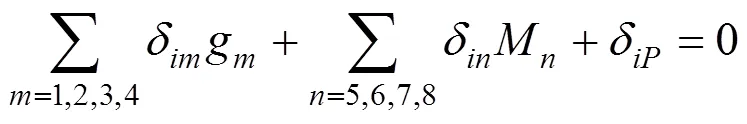
式中：为m单位力作用下，接缝i处产生的相对位移；δin为n单位弯矩作用下，接缝i处产生的相对位移；δip为外荷载在接缝i处产生的竖向位移。

1.5 方程系数计算

δ，和利用材料力学的公式求解，并规定位移与作用力方向一致时取正值，反之取负值，具体取值见下式：

式中：为主梁宽度；为单位荷载作用在主梁中央产生的挠度；为单位荷载作用在主梁悬臂端时产生的挠度；为单位扭矩产生的截面扭转角；′为单位弯矩作用在悬臂端时产生的扭转角；为单位弯矩作用在悬臂端时产生的挠曲角。

1.6 主梁刚度分配系数

桥梁运营过程中，除了湿接缝会发生损坏外，在各种荷载的作用下，裂缝的产生导致主梁发生了不同程度的损伤，在损伤处的刚度也发生相应变化。这时刚接梁法荷载横向分布计算中的和δ会根据主梁刚度的变化而变化。

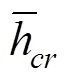
式中：h为受拉区混凝土退出工作的程度；为裂缝开展程度；l为裂缝间距；l为开裂范围；为裂缝条数。

再将式(12)和(13)代入式(14)求得开裂截面的损伤刚度：

式中：为在役桥梁外力对开裂截面换算截面形心轴产生的弯矩；M为有效预应力对开裂截面换算截面形心的弯矩[12−13]。

邬晓光等[14]认为主梁发生损伤后，挠度由2部分组成，即梁体完好时产生的挠度和梁体由于开裂刚度损伤产生的附加挠度Δ，并提出一个刚度分配系数的概念，假设荷载按该刚度分配系数分布，即(1−)和。以跨中开裂梁段为例，刚度分配系数计算如下：

挠度的增加等效视为抗弯刚度的折减：

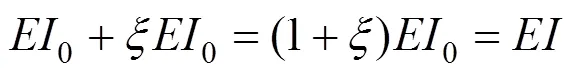
代入式(14)得：

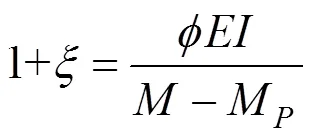
式中：为梁体完好情况下结构抗弯刚度；0为考虑裂缝引起刚度损伤情况下结构抗弯刚度。

1.7 方程化简

现在以一座5片T梁组成的拼宽桥梁为例，旧桥由3片T梁组成，通过单侧拼宽2片T梁成为拼宽结构，横断面见图2。在进行刚接梁法荷载横向分布计算时，旧桥由于发生抗弯刚度损伤，正则方程中的和会根据主梁刚度的变化而变化。

图2 拼宽T梁桥横断面

假设拼宽桥梁中的3片旧梁刚度发生不同程度损伤，刚度分配系数分别为1，2和3，新梁完好。

则正则方程中的相应系数发生变化：

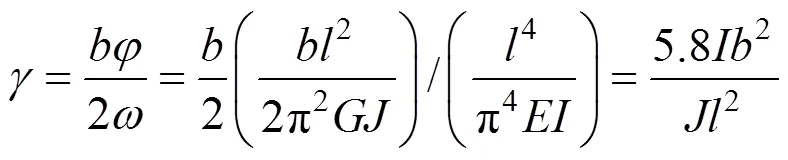
混凝土剪切模量取0.425，则有

得到新的系数矩阵：

2 算例分析

福建某40 m拼宽T梁桥，原为5梁式，采用单侧拼接4片相同形式的T梁、上部结构通过湿接缝及横隔板相连、下部结构不连接的方式进行拓宽。横断面形式如图3所示。拓宽后桥面宽度=18.50 m，主梁宽度=2.10 m，翼板长度1=1.05 m，厚度1=0.16 m。

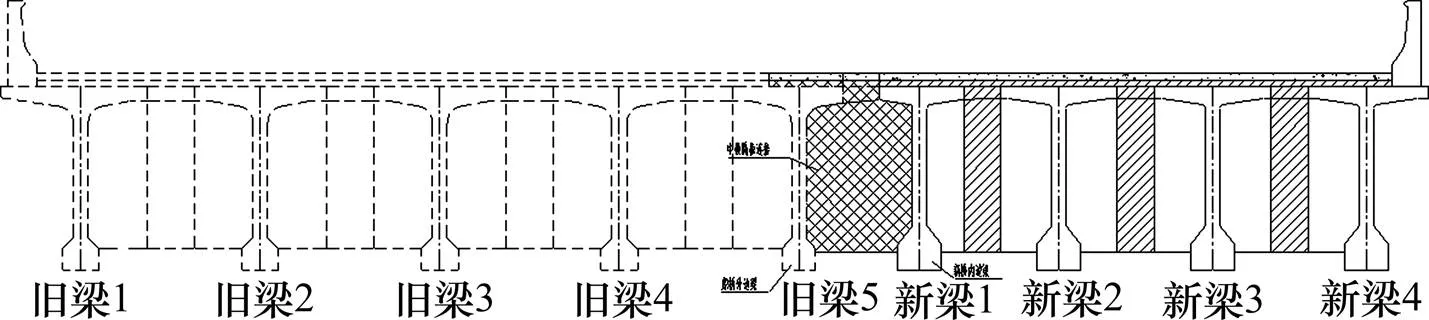
图3 横断面形式

在进行实桥荷载试验之前，对全桥进行外观检查，调查湿接缝及主梁跨中底部病害情况。通过外观调查结果得到裂缝统计特征，代入1.6节中的相关公式计算主梁刚度分配系数。

然后根据湿接缝病害调查结果，初步确定可能发生损伤的湿接缝位置。采用一辆40 t重的汽车荷载，车轮位置靠近损伤湿接缝，将传感器布置在主梁跨中及损伤湿接缝位置，测量汽车荷载作用在损伤湿接缝位置的竖向位移最值，根据1.3节中的相关公式计算接缝损伤系数，并确定竖向剪力折减系数μ。

以单位正弦荷载作用在旧梁1上为例介绍考虑旧桥损伤的拼宽T梁桥荷载横向分布计算方法，首先将主梁刚度分配系数代入新的系数矩阵，并通过式(7)计算求得竖向剪力g，再将竖向剪力g代入考虑竖向剪力折减系数的式(1)即可求得单位正弦荷载作用在旧梁1上时的横向分布影响线竖标值，其余主梁的荷载横向分布计算与此类似。

荷载试验工况考虑3辆车跨中布载，纵桥向布置在跨中截面，横桥向为中载布置。具体布置位置如图4和图5所示。

单位：cm

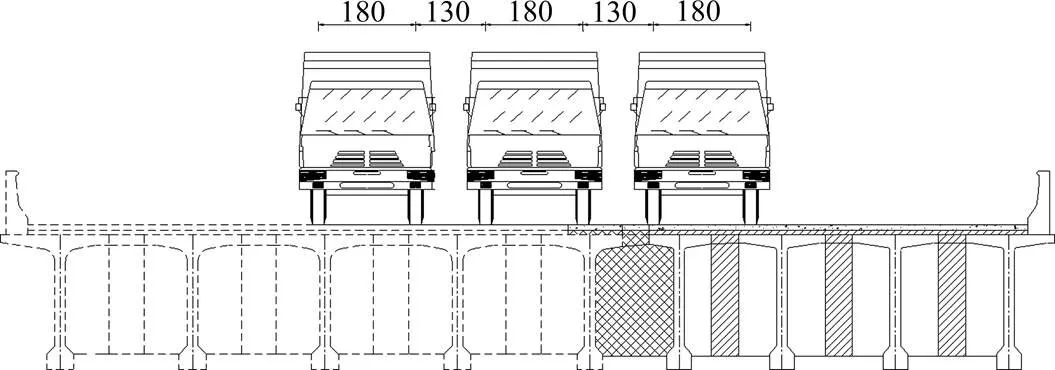
单位：cm

试验车辆参数如表1所示。

表1 加载车辆重量表

表2 实桥荷载试验挠度测量值

图6 有限元模型

3 综合比较研究

表3列出了在试验工况作用下，不同方法对拼宽桥各片主梁的横向分布系数计算结果，包括刚接梁法、考虑旧桥损伤的刚接梁法、有限元数值法及荷载试验法。表4将各计算结果与荷载试验计算结果作了比较分析。

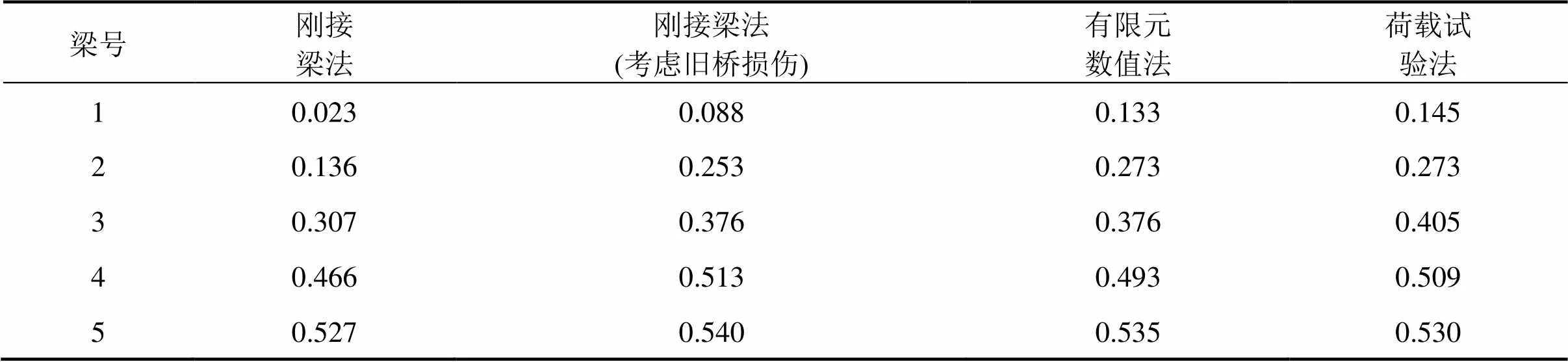
表3 横向分布系数计算结果

表4 各计算方法横向分布系数较荷载试验计算结果误差绝对值

从表4可以看出：1) 传统刚接梁法计算的横向分布系数偏小，与荷载试验结果存在较大偏差，这是因为试验桥梁在拼宽之前已经运营10 a之久，主梁刚度退化明显，导致旧梁挠度变大，使得旧梁的横向分布系数有所增大，传统刚接梁法没有考虑这一方面的影响，使得其计算数值偏小，对拼宽桥梁设计偏于不安全；2) 考虑旧桥损伤建立的有限元模型计算得到的横向分布系数与荷载试验结果误差均在8.3%以内，反映了本文建立的有限元模型能够较好地反映拼宽桥梁的实际受力，验证了模型的正确性；3) 考虑旧桥损伤的刚接梁法计算的横向分布系数与荷载试验、有限元数值法计算结果较为接近，旧梁1出现较大比值的原因是由于三者横向分布系数均较小，使得比值显得偏大造成的结果； 4) 采用本研究推导的考虑旧桥损伤的刚接梁法计算的横向分布系数较传统刚接梁法有所差异，但与有限元数值法和荷载试验得到的横向分布系数较为接近，反映了在计算拼宽桥梁横向分布系数时，不能忽略旧桥损伤对拼宽桥梁整体受力的影响，本研究在传统刚接梁法理论的基础上推导的计算方法能够较好地考虑这一方面的不足。

4 结论

1) 计算拼宽桥梁横向分布系数时，有必要考虑旧桥损伤的影响，本研究将竖向剪力折减系数和主梁刚度分配系数引入传统的刚接梁法计算理论，并重新推导了刚接梁法系数矩阵，算例结果证明本研究推导的考虑旧桥损伤的刚接梁法能够较好地反映拼宽桥梁的横向分布特性，为以后拼宽桥梁荷载横向分布计算提供参考。

2) 考虑旧桥损伤建立的有限元模型计算得到的横向分布系数与试验方法得到的结果接近，能够较好地反映拼宽桥梁的实际受力; 传统刚接梁法计算的横向分布系数较试验方法得到的数值偏小，对拼宽桥梁设计偏于不安全，计算拼宽桥梁内力时不能忽略旧桥损伤的影响。

[1] WANG Guanghui, SHEN Lian, WEI Chenglong. Research on strengthening existing bridges by widening[J]. Advanced Materials Research, 2013, 639− 640: 1092−1095.

[2] Bogaert P V. Bridge design: Conbining old and new into aesthetic structures[C]// International Conference on New Dimensions in Bridge, Singapore, 2006: 77−88.

[3] Tienp M, Van-Chuong N. Application of the external prestressing method in the repair, strengthening and widening of the Saigon Bridge[C]// Proceedings of the EASTS Conference 2001 in Hanoi,Vietnam, 2001: 24−27.

[4] Swett G, Stanton J, Dunston P. Methods for controlling stresses and distoritions in stage-constructed steel bridge[J]. Transportation Research Record Journal of the Transportation Research Board, 2000, 1712(1): 164−173.

[5] 赵煜, 张珂. 既有桥梁拓宽后承载潜力研究[J]. 长安大学学报(自然科学版), 2003, 23(1): 51−53. ZHAO Yu, ZHANG Ke. Load carrying capacity of broadened existing bridge[J]. Journal of Chang’an University (Natural Science), 2003, 23(1): 51−53.

[6] 王浩, 朱若溪, 张肈红. 连接刚度对加宽桥梁荷载横向分布的影响分析[J]. 公路, 2013, 7: 144−146. WANG Hao, ZHU Ruoxi, ZHANG Zhaohong. Impact analysis of connection stiffness on load transversal distribution factor of widening bridges[J]. Highway, 2013, 7: 144−146.

[7] 黄立浦, 曹素功, 常柱刚. 旧桥拓宽加固中荷载横向分布系数的变化规律[J]. 中外公路, 2017, 37(4): 108−112. HUANG Lipu, CAO Sugong, CHANG Zhugang. Change rule of load transversal distribution factor in widening and strengthening of old bridges[J]. Journal of China & Foreign Highway, 2017, 37(4): 108−112.

[8] 毛建平, 覃乐勤, 蒙方成. 拼宽箱梁横向分布效应理论与试验研究[J]. 中外公路, 2017, 37(5): 166−169. MAO Jianping, QIN Leqin, MENG Fangcheng. Theoretical and experimental study on transversal distribution factor of widening box girder[J]. Journal of China & Foreign Highway, 2017, 37(5): 166−169.

[9] 刘莉, 单婷婷. 拼宽箱梁桥荷载横向分布计算及应用[J]. 中国市政工程, 2016, 3: 17−19. LIU Li, SHAN Tingting. Calculation and application of load transversal distribution factor of widening box girder bridge[J]. China Municipal Engineering, 2016, 3: 17−19.

[10] 何启龙, 钱若霖, 贺书磊, 等. 不同横向刚度劣化类型下的拼宽桥受力影响[J]. 沈阳大学学报(自然科学版), 2018, 30(2): 151−156. HE Qilong, QIAN Ruolin, HE Shulei, et al. Impact of widening bridge under different types of lateral stiffness degradation[J]. Journal of Shenyang University (Natural Science), 2018, 30(2): 151−156.

[11] 袁桂芳. 装配式板梁铰缝损伤识别模型的研究[J]. 公路, 2017, 8: 75−80. YUAN Guifang. Research on model for damage identification of hinged joints of prefabricated slab bridges[J]. Highway, 2017, 8: 75−80.

[12] 赵煜, 周博, 贺拴海, 等. 基于裂缝特征的PC简支梁损伤刚度评估方法[J]. 长安大学学报(自然科学版), 2011, 31(4): 39−44. ZHAO Yu, ZHOU Bo, HE Shuanhai, et al. Damage stiffness assessment method based on fracture characteristics of PC simply-supported beam[J]. Journal of Chang’an University (Natural Science), 2011, 31(4): 39−44.

[13] 董水英. 预应力混凝土简支梁开裂后挠度模型试验研究[D]. 西安: 长安大学, 2010: 19−24. DONG Shuiying. Model experimental study of deflection of the cracked prestressed concrete beam[D]. Xi’an: Chang’an University, 2010: 19−24.

[14] 邬晓光, 钱若霖, 苏佩. 考虑刚度损伤的装配式T梁桥横向分布计算[J]. 公路交通科技, 2018, 35(6): 61−66. WU Xiaoguang, QIAN Ruolin, SU Pei. Calculation of transverse distribution of assembled T-beam bridge considering stiffness danage[J]. Journal of Highway and Transportation Research and Development, 2018, 35(6): 61−66.

[15] 钱寅泉, 周正茂, 王素娟, 等. 装配式小箱梁桥荷载横向分布数值分析与试验[J]. 公路交通科技, 2012, 29(1): 86−90. QIAN Yinquan, ZHOU Zhengmao, WANG Sujuan, et al. Numerical experiment of lateral load distribution of fabricated small box girder bridge[J]. Journal of Highway and Transportation Research and Development, 2012, 29(1): 86−90.

Calculation of load transverse distribution of widening T-beam bridge considering old bridge damage

WU Xiaoguang, HUANG Cheng, LI Yuanjun, YIN Yue

(Highway School, Chang’an University, Xi’an 710000, China)

The existing research on the load transverse distribution of widening bridge is based on the traditional calculation method of the transverse distribution, and there are few studies on the calculation of load transverse distribution of widening T-beam bridge under the condition of old bridge damage. In order to improve the calculation accuracy of the internal force of widening T-beam bridge, considering stiffness damage of wet-joint and stiffness damage of main girder, the reduction ratio of vertical shear force and girder stiffness were determined by load test and visual inspection. Finally, reasonable computing method was deduced on the basis of traditional rigid-jionted beam method. Relying on a 9-girder simply supported T-beam bridge with unilateral widening, the transverse distribution factor calculated by method of this study were compared with calculation results of traditional rigid-jionted beam method、finite element numerical simulation、load test method. The results show: When calculating the transverse distribution factor of widening T-beam bridge, the old bridge damage should be considered, and the calculation method deduced by this study can reflect the actual stress of widening bridge; The transverse distribution factor of widening bridge calculated by traditional rigid-jionted beam method are unsafe.

bridge engineering; transverse distribution factor; rigid-jionted beam method; stiffness damage; wet joint stiffness damage

U441.2

A

1672 − 7029(2019)09− 2233 − 07

10.19713/j.cnki.43−1423/u.2019.09.014

2018−11−26

福建省交通运输厅2014年科技计划资助项目(Y-201400006)；贵州省交通运输厅科技项目(2015-121-024-1)

邬晓光(1961−)，男，湖北英山人，教授，博士，从事桥梁设计理论与桥梁检测加固研究；E−mail：wxgwst.cn@126.com

(编辑 涂鹏)