流模式下有向近似覆盖图算法研究
2019-03-22李晓光
张 昕 李晓光
(辽宁大学信息学院 沈阳 110036) (zhangxin1979@hotmail.com)
图作为一种重要的数据结构,一直有着广泛的应用,特别是随着信息技术的发展,在诸如通信网络中路由选择与资源优化、社交网络中用户关系与兴趣点分析、交通网络分析以及计算几何学与计算生物学等重要应用领域中,大量的数据均以图结构作为抽象对象,进而开展各种复杂的计算与分析研究[1].因此,大规模图数据相关研究逐渐成为许多研究与应用领域的一项重要的基础性工作.但由于数据量的飞速增长,以及图结构自身的复杂性,大规模图数据的存储与计算代价通常较高,很难高效地支撑后续的研究应用工作.
针对这种情况,研究人员进行了大量相关工作,其中求解近似覆盖图是目前一种代表性的研究方法,得到广泛的关注.该方法通过近似解代替精确解,以此降低存储精度需求,进而降低存储与计算代价.考虑到在许多应用中,对图中节点间连接信息的需求精度不高,可以在保持节点间连通性的前提下删除大量边,仅保留节点间近似的路径长度,形成对原图的一种近似覆盖.这种方法通常以2个参数α与β约束近似图与原图中节点间路径长度的变化程度,称为原图的(α,β)-覆盖.文献[2]提出一种确定性算法,可以获得(k,k-1)-覆盖,该算法适用于无向无权图,其时间复杂度为O(m+n),空间复杂度为O(k×n),其中n与m分别为图数据中节点与边的数量.同时,该文献还证明了对于无向图的(1,6)-覆盖,在空间复杂度为O(n)的情况下,都能够在时间复杂度最高为O(mn).文献[3]提出一种适用于加权无向图的随机性算法,该算法可以获得(2k-1,0)-覆盖,其时间复杂度为O(m+n),空间复杂度为O(k×n).文献[4]则提出了与文献[3]相同使用环境与目标的非随机性算法,其时间复杂度也同样为O(m+n).
较早的研究工作多集中针对静态无向图,考虑到数据的动态变化,特别是边的插入与删除,文献[5]提出的方法可以在O(n)条边的插入与删除过程中,获得(3,0)-覆盖与(5,0)-覆盖,处理每次边变化的时间复杂度与原图最大度值呈线性关系,算法所得到(3,0)-覆盖边数为O(n),而(5,0)-覆盖边数则为O(n).文献[6]提出了一种可更加快速获得(2k-1,0)-覆盖的随机动态算法,空间复杂度为O(k×n),处理每次边变化的时间复杂度为O(mn).文献[7]提出的方法能够动态构造(1+ε)-覆盖,其更新时间为O(logn),其中ε为常数参数.
随着数据量级以及变化速度的不断增大,流模式下近似覆盖图的计算逐渐成为研究热点.文献[8]提出了一种适用于无向无权图的随机算法,该算法仅通过1次扫描可以获得(2k+1,0)-覆盖,其空间大小为O(k×n),平均处理1条边的时间为O(k2×n×logn),所需内存大小为O(k2×n×logn)字节.文献[9]提出的方法可以通过1次扫描获得空间大小为O(k×n)的(2k-1,0)-覆盖,其整体时间复杂度为O(m+n),所需内存大小为O(k×n).文献[10]提出了一种非严格流模式下的算法,该算法假定数据传输以块的模式进行,内存中保留与节点有关的信息,算法所需的内存大小为O(n),所需外部存储块为O(nB),其中B是外部存储块的大小.文献[11]提出基于采样的流模式近似覆盖图算法,该算法对每条边的平均处理时间为O(max{llogn,1}),其中l为子图数量.
近年来,基于其他覆盖形式以及不同距离含义的研究也得到一定程度的关注,例如图的近似树形覆盖[12-14]以及有向图环境下基于往返距离[15-17]与平面距离的近似覆盖图[18-19]等.综合看来,目前的研究工作大多集中于无向图环境,有少量针对有向图的研究,但其侧重点以及应用环境与传统方法相比差异较大.本文针对有向图环境,研究基于传统距离含义的近似覆盖图计算,定义相关概念,进而给出具体算法,并通过理论分析以及实验,说明算法的有效性.
本文的主要工作有3个方面:
1) 针对有向图特点,重新定义近似覆盖图的相关概念,包括簇集以及簇边、桥边、自由边这3类关键边;
2) 分析了求解近似覆盖图过程中,簇集的形成、3类关键边的确定以及关键边类型可能发生的转化,论证了3类关键边形成的子图满足覆盖因子为(3,2)的近似覆盖图定义;
3) 给出了在流模式下求解有向图近似覆盖的算法,依据在模拟数据集上的实验结果,对该算法进行了定量分析,并与无向图近似覆盖算法进行了定性对比分析,综合说明算法较佳的时空效率.
1 相关概念
本节给出有向图的近似覆盖图计算所需相关定义的形式化描述,并论证其合理性.
1.1 基本定义
本文所需基础定义为图G=(V,E),其中,
V:图中节点的集合;
E:图中边(节点对间的连接)的集合;
deg(v):图中与节点v(v∈V)连接的边数,称为该节点的度;
deg_in(v):有向图中射入节点v的边数,称为该节点的入度;
deg_out(v):有向图中由节点v射出的边数,称为该节点的出度;
d(u,v):图中节点u到v经过最少的边数,称为节点对(u,v)间的距离.若u到v之间不存在连通路径,记距离d(u,v)为正无穷.无向图中d(u,v)=d(v,u);
Pre(x):节点x所有前趋节点的集合,即对于任意的节点a,若a,x∈E,则a∈Pre(x);
Next(x):节点x所有后继节点的集合,即对于任意的节点b,若x,b∈E,则b∈Next(x);
N(x):节点x的邻节点集合,且包含x自身.
图G的近似覆盖图是一个与图G拥有相同的节点集合的子图,且该子图保存了图G中任意节点对之间距离的近似.
定义1. 近似覆盖图.设图G=(V,E),给定参数α≥1,β≥0,若对于G′=(V,E′)中任意的节点对(u,v),均满足:
d′(u,v)≤d(u,v)×α+β,
(1)
则称子图G′是图G的近似覆盖图,记作(α,β)-覆盖,参数α与β称为覆盖因子.
式(1)中d′(u,v)表示节点对(u,v)在G′中的距离.依参数α=1或参数β=0,称对应的近似覆盖图为简单加性近似覆盖图或简单乘积近似覆盖图.若参数α与β取值过小,则近似覆盖图与原图的差异不大,降低存储计算开销的作用不明显,而参数α与β取值过大的话,则相对原图来说细节损失过多,不适合进一步的计算分析.因此,适当的参数选取才能够较为充分地发挥近似覆盖图的作用.参考现有研究工作的参数选择,本文设定覆盖因子α=3,β=2,即计算图G的(3,2)-覆盖.
1.2 簇 集
本文算法基本思路为获得原图的一个适当的聚簇结果,有选择地删除簇内及簇间的部分边,由此得到原图的一个近似覆盖.本节给出簇集以及相关定义如下.
定义2. 簇集.令x1,x2,…,xk为节点集V中的若干节点,取其中每个节点前驱集与后继集的不小于l的子集,分别合并为k个集合,即:
Up(xi)⊆Pre(xi),|Up(xi)|≥l,
(2)
Down(xi)⊆Next(xi),|Down(xi)|≥l,
(3)
Cl(xi)=Up(xi)∪Down(xi)∪{xi},
(4)
其中,k≥1,l≥1且1≤i≤k,若满足:
(5)
则称这些集合{Cl(xi)}为图G的l类簇集.
图G的l类簇集中,称每个集合Cl(xi)为簇,节点xi为该簇的中心节点,分别称集合Up(xi)与Down(xi)为该簇的上簇节点与下簇节点,合称该簇的簇节点,而不属于任何簇的节点则称为自由节点.由定义1可见,簇之间可能存在重叠,同时属于多个簇的节点,其在各个簇中的角色也可能不同.对于簇节点x,依据节点x为这些簇的上簇节点或下簇节点,对应簇的中心节点集合分别表示为center_up(x)或center_down(x).图1为一个简单的3类簇集示意,为清晰起见,省略了簇节点之间包含在簇内的边.图1中节点a,b分别为簇Cl(a),Cl(b)的簇中心节点,同时节点a在簇Cl(b)中为簇节点,节点b在簇Cl(a)中也为簇节点.节点c同时属于2个簇,且均为下簇节点,因此集合center_down(c)={Cl(a),Cl(b)}.
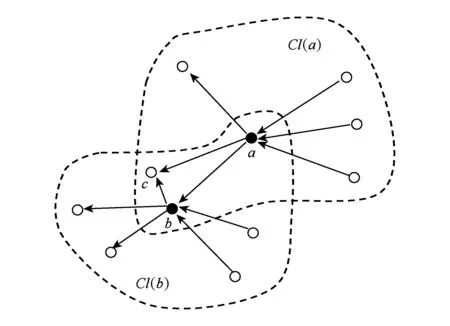
Fig. 1 3-clustering图1 3类簇集
定义3. 自由邻节点集合.对于图G中的节点v,其自由邻节点集合为
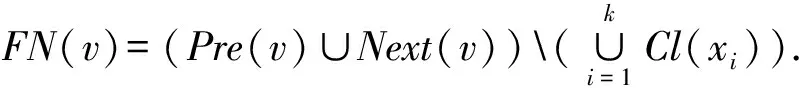
(6)
由定义2可以看出,1个节点可以同时属于多个簇,所以1个l类簇集最多可以有n个簇,每个簇至少包含l个节点以及2l条有向边.结合定义3可知,若给定1个l类簇集,对于图中任意的节点v来说均有|FN(v)|<2l成立,则该l类簇集显然是最大化的.
1.3 关键边
对于图G中的任意边u,v是否保存在近似覆盖子图G′中,本节分为簇边、桥边与自由边3类关键边讨论,其中与簇中心节点相连的边均保存为该簇的簇边,余下分3种情况讨论:
1) 当节点u与v同属1个簇Cl(x),若u∈Up(x),v∈Down(x),则边u,v不需要保存;除此之外,则临时标记边u,v为自由边.显然,边的始点与终点分别为同簇内的上簇节点与下簇节点时,存在由簇中心点转接的长度为2的路径,由原图中去除该边不影响节点间可达性,且节点间距离仅增加1.
2) 当节点u与v分属2个不同簇Cl(x1),Cl(x2)时,进一步分3种情况来讨论:
① 当u∈Down(x1),v∈Up(x2)时,边u,v保存为连接簇Cl(x1)与Cl(x2)的桥边.
② 当u∈Up(x1),v∈Up(x2)时,若不存在以节点v为终点的桥边a,v,则临时标记边u,v为自由边.如图2所示,节点x1与x2为簇中心节点,节点u与v分别为各簇的上簇节点,图2中虚线边为簇间桥边,若该桥边不存在,则边u,v需保存于近似覆盖图中,以保证节点u与v之间可达.
③ 当u∈Cl(x1),v∈Down(x2)时,若簇对Cl(x1)与Cl(x2)之间不存在桥边,则临时标记边u,v为自由边.如图3所示,节点x1与x2为簇中心节点,节点u为Cl(x1)中的簇节点,节点v为Cl(x2)中的上簇节点,图3中虚线边为簇间桥边,若该桥边不存在,则边u,v需保存于近似覆盖图中,以保证节点u与v之间可达.
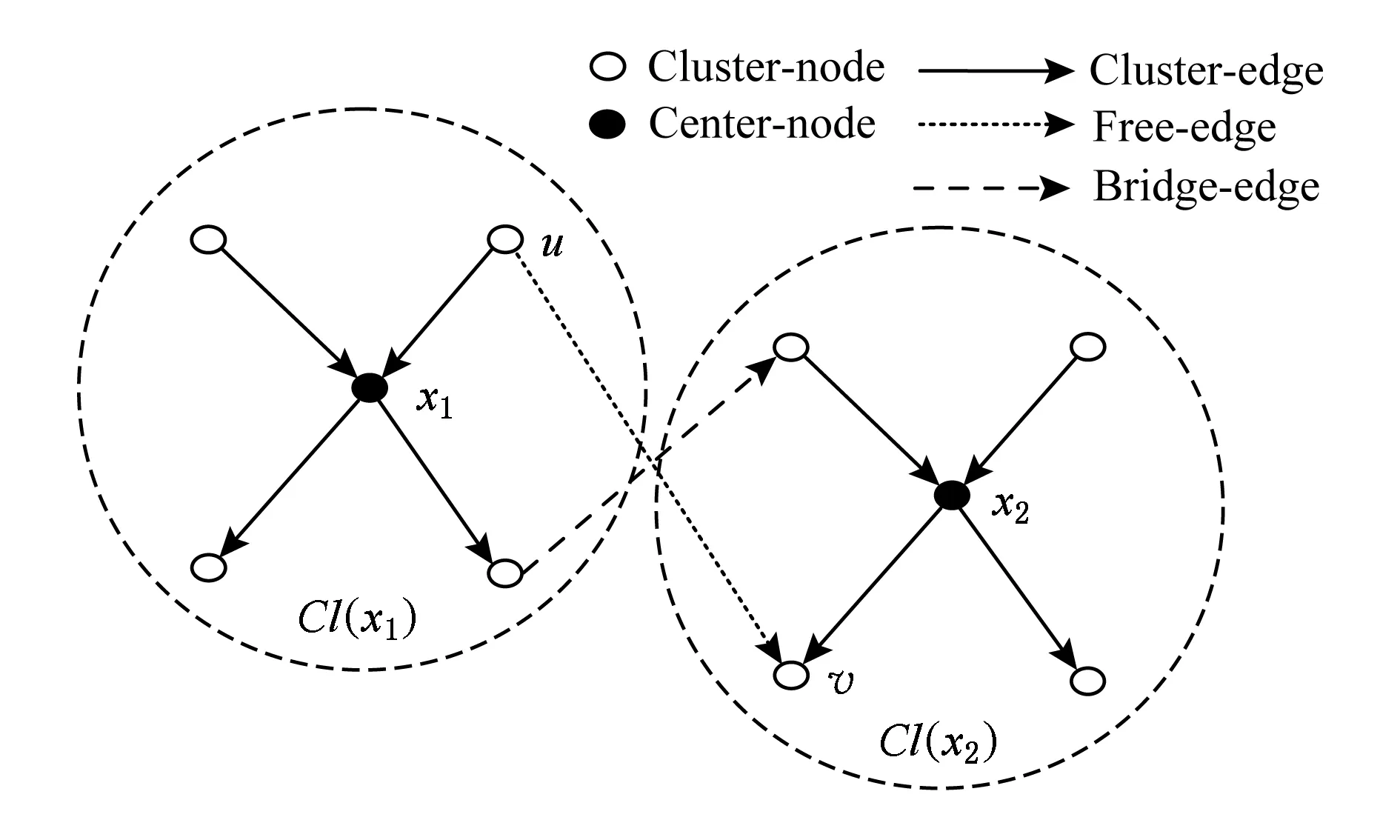
Fig. 3 Edge between different cluster from Cluster-node to Down-node图3 簇节点指向下簇节点的簇间边
3) 节点u与v中的任意一个节点为自由节点,则临时标记边u,v为自由边.
由于同一节点可能属于多个簇,因此上述3种情况可能有所重叠,所以明确不同类型边的保存规则有4项:
① 簇边均需保存;
② 至少满足1对簇间桥边定义,需保存;
③ 1个端点为自由节点的自由边需保存;
④ 簇内自由边与簇间自由边,若不存在包含边的2个端点,且始点为上簇节点,终点为下簇节点的簇,则需保存.
考虑聚簇过程如下:当临时自由边数量达到一定阈值时,对其进行聚类形成新簇,具体来说当以某节点u为始点及终点的临时自由边数量均超过阈值l时,则形成新簇Cl(u),节点u为该簇中心节点,节点u的所有临时自由前趋节点与自由后继节点分别为该簇的上簇节点与下簇节点.
在聚簇过程中部分临时自由边会转为簇边或桥边保存,而部分临时自由边可能转变为无需保存的冗余边从而被删除,最终所得近似图覆盖子图中可能仍保存有未被删除的自由边,因此近似图覆盖子图是由簇边、桥边以及自由边形成的集合.
1.4 合理性证明
由1.3节对簇边、桥边以及自由边的描述,可以证明对于给定有向图G=(V,E)及图上的1个l类簇集,若子图G′=(V,E′)是图G的(3,2)-覆盖,即满足:
d′(u,v)≤3d(u,v)+2,
(7)
则E′为这3类关键边的集合.为此,观察图G中任意边u,v在子图G′中对应的以u为起点且v为终点的路径,可分4种情况讨论.需要注意的是,在聚簇过程中,簇内自由边或簇间自由边可能转变为新簇内上簇节点指向下簇节点的冗余边,从而被删除,使得原来长度为1的自由边转变成了2条簇边形成的长度为2的路径:
1) 当节点u,v中至少有1个节点是簇中心点时,则边u,v为图G′中的1条簇边,此时d′(u,v)=1.
2) 当节点u,v中至少有1个节点是自由节点且没有簇中心节点时,则u,v为图G′中的1条自由边,此时d′(u,v)=1.
3) 当节点u,v同属1个簇Cl(x)时,若u∈Up(x),v∈Down(x),则边u,x,x,v为图G′中的簇边,此时d′(u,v)=2.否则边u,v为图G′中的簇内自由边,此时d′(u,v)=1或2.
4) 当节点u,v分属2个不同簇Cl(x1),Cl(x2)时,又细分为4种情况:
① 当u∈Down(x1),v∈Up(x2)时,则边u,v为图G′中的桥边,此时d′(u,v)=1;
② 当u∈Down(x1),v∈Down(x2)时,若图G′中存在桥边u,a,其中a∈Up(x2),则该桥边与簇边a,x2,x2,v构成图G′中的1条路径,此时d′(u,v)=3.否则,u,v为图G′中的簇间自由边,此时d′(u,v)=1或2;
③ 当u∈Up(x1),v∈Up(x2)时,若图G′中存在边a,v,其中a∈Down(x1),则簇边u,x1,x1,a与该边构成图G′中的1条路径,此时d′(u,v)=3.否则,u,v为图G′中的簇间自由边,此时d′(u,v)=1或2;
④ 当u∈Up(x1),v∈Down(x2)时,若图G′中存在桥边a,b,其中a∈Down(x1),b∈Up(x2),则图G′中存在路径{u,x1,x1,a,a,b,b,x2,x2,v},此时d′(u,v)=5.否则,u,v为图G′中的簇间自由边,此时d′(u,v)=1或2.
由以上分析可以看出,除最后1种情况外,均满足d′(u,v)≤3d(u,v).将观察范围扩展为图G中的路径D={u1,u2,u2,u3…ui-1,vi},显然有:

(8)
再观察前述最后1种情况(同时也是最坏情况),即每个节点uj分别属于簇Cl(xj),其中1≤j≤i,且图G中相邻节点在子图G′中需要经过始点所在簇中心节点以及桥边转接至相邻簇,再经相邻簇中心节点连接至终点,因这2部分子路径的长度分别为3和2,则对于图G中边u1,u2来说,有:
d′(u1,u2)=3d(u1,u2)+2.
(9)
式(9)中右部第1项为簇Cl(x1)中2次转接及1次桥边转接,第2项为簇Cl(x2)中的2次转接.进一步考虑图G中路径D的下一条边u2,u3,在子图G′中节点u1到达u3则需要多经过1个簇,因此增加2次簇中转接及1次桥边转接,即式(10)中右边第2项:
d′(u1,u3)=3d(u1,u2)+3d(u2,u3)+2.
(10)
以此类推,可得:
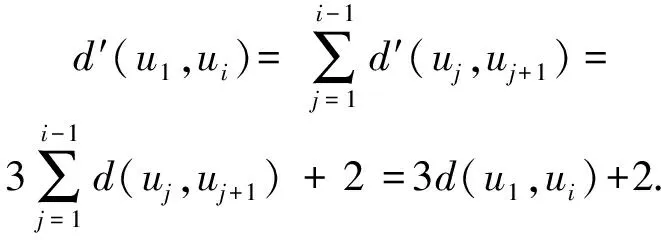
(11)
因此可得,在所有情况下子图G′均是满足定义1覆盖因子为(3,2)的近似覆盖图,即图G的(3,2)-覆盖.
2 流模式下有向近似覆盖图算法
本节给出有向图中计算近似覆盖图算法的基本思想以及算法中需要保存的临时信息,以伪代码的形式给出算法具体过程的描述,并分析了算法空间效率.
2.1 算法基本思想
图数据以边的形式存储,按边的端点排序后以流模式输入.算法或者建立上簇节点与下簇节点均至少为l个的新簇,或者将输入边的端点添加至已存在的簇.在处理节点的同时,输入边可能保存为簇边或桥边,也可能被抛弃,剩余边均标记为自由边,临时保存在候选自由边集合中.当候选自由边集合大小超过阈值时,将对其进行聚类形成新簇,这样即使簇边u,v的起点u距离终点v较远,使得边的输入位于数据流早期时,仍然可以形成以v为中心节点的簇.
具体算法中,每个节点x存储2种信息:
1) 标识节点x是簇节点、自由节点或簇中心点的状态标志.若节点x为簇节点,还需存储包含x的所有簇的标志,以及集合center_up(x)与center_down(x);若节点x是某个簇的中心节点,则需保存该簇的Up(x)与Down(x)集合.
2) 临时自由边的集合Tpre(x)与Tnext(x).其中Tpre(x)包含了节点x的所有前趋自由边,Tnext(x)包含了节点x的所有后继自由边.随着算法的运行导致节点状态发生改变,这2个集合中可能会包含一些非自由边,将在自由边集聚类时删除.
簇边保存在对应簇边集合中,桥边存储在矩阵Bridge中,Bridge[i,j]存储连接簇Ci到簇Cj的桥边集合.若簇Ci与簇Cj之间不存在桥边,则Bridge[i,j]显然为空.但反之未必成立,即Bridge[i,j]为空时,可能存在连接簇Ci与Cj的桥边,保存在Tpre(x)或Tnext(x)中.
2.2 算法描述
算法通过判断边端点类型来决定边是否需要保存以及保存为何种类型.若端点包含簇中心点则保存边为簇边,否则先考虑是否满足桥边定义,之后判断是否属于同簇内上簇节点指向下簇节点,最后分3种情况考察是否为自由边.当节点自由边数量超过阈值时,开始聚集新簇,并删除新簇中可能的冗余边.
算法1. 流模式下有向近似覆盖图的计算.
输入:前一时刻有向图G、当前到达的边x,y;
输出:当前时刻聚簇以及3类关键边.
① ifx或y为簇中心点
③ ify为自由节点
④ 添加y至Down(x);
⑤ 更新y标识为簇节点;
⑥ end if
⑦ ifx为自由节点
⑧ 添加x至Up(y);
⑨ 更新x标识为簇节点;
⑩ end if
〈u,v〉;
算法1中,簇边与桥边自初次保存后一直存在,端点为自由节点的自由边在端点标识改变之前一直保存,之后可能随着聚集新簇成为簇边,或成为桥边,或继续保存为自由边,还可能任意一个保存条件都不再满足从而删除.显然,算法满足2.3节给出的不同类型边的保存规则.
2.3 算法分析
依据2.2节给出的算法描述,本节分析该算法在有向图中求得的近似图覆盖子图边集的大小.由图4所示,有向图中的节点可看作上下2部分,图4中的边均由上半部分中指向下半部分.这种情况下,若删除其中的任意1条边,则某2个节点之间不再连通,称这种结构为结构.

Fig. 4 structure图4 结构
考虑图G的节点v,若满足deg_in(v)≥n且deg_out(v)≥n,则进行聚类操作形成簇Cl(v).设簇总数为k,则最坏情况下簇边的数量为(n-k)×k,当k=n2时达到最大值,即簇边的数量不超过O(n24).
考虑与簇Cl(v)相连的节点u,以节点u为始点连接簇Cl(v)的边集合u,X,则满足X⊆Up(v)或者X⊆Down(v),但2者不会同时满足.因此聚类操作得到2部分结果:或是聚类成簇,则除了簇边以外的桥边及自由边形成结构;或是部分节点的出度或入度之一小于n,不足以形成新簇,保存为自由边.其中结构显然可以判断出边的数量不超过O(n24).
对于满足deg_in(v) 由此可得,图G′=(V,E′)为关联到n类最大化簇集的(3,2)-覆盖,则G′包含O(n24)条边. 实验运行的硬件环境为英特尔酷睿双核处理器,主频2.2 GHz、内存8 GB、软件环境为Linux操作系统,算法由C语言编写实现,使用gcc进行编译.实验数据使用幂率模型生成的人工数据集,此类图中节点的度分布呈现幂率分布,与互联网、社交网、交通网以及蛋白质生物网络等现实世界中的大规模图数据类似,普遍具有小世界与无标度等宏观拓扑特性[20-22],是图分析领域广泛选用的实验数据集,适用于本文的算法实验分析.本文具体采用基于递归矩阵(R-MAT)的网络模型[23],生成节点数量为8 000,平均度分别为50,200,800,3 200的4个人工图数据集,对比算法在不同数据集上的运行效果. 算法的具体实现中,使用散列表存储节点所需的信息,为每个节点保存1个32 b的标签作为散列表键值.当1条有向边以流的形式到达时,首先判断该边的2个端点是否首次出现.若是首次出现的新节点,则创建1个与该节点对应的散列表项,否则根据节点的标签检索到对应的散列表项并根据需要进行更新. 对于非对称的桥边集矩阵Bridge,也使用散列表来保存桥边列表,并采用64 b的散列键值.当1条有向边判定为桥边,需要保存至列表中时,将该边的2个端点各自的32 b标签值连接为1个64 b键值,这样由标签值的连接次序就可以区别同一对节点对应的2条有向边.桥边的存储按其64 b键值将该边插入到桥边列表的相应位置,而当检索某2个簇间的桥边是否存在时,则同样按其64 b键值在散列表中进行查找. 本文实验中主要考察3项指标: 1) 平均伸展率是指图中所有节点对(x,y)在近似覆盖图与原图中距离之比d′(x,y)d(x,y)的平均值.实际计算中普遍使用采样估算值,即随机选取一定比例的节点对进行计算,在大幅减少计算量的同时,结果的精度也有一定的保证.依据定义所得理论上限值通常称为最大伸展率,由覆盖因子决定,而在实际上近似覆盖图中的节点对并不都处于理论上的极限情况,因此平均伸展率比最大伸展率要小. 2) 近似图覆盖比例是指近似图覆盖中边的数量与原图中边的数量之比,体现算法的空间效率. 3) 运行时间即算法在数据集上运行的时间,体现其时间效率. 图5所示是近似图覆盖比例随着聚簇阈值的改变表现出的不同情况,图5中4条折线分别表示本文算法在4个不同人工图数据集上运行的结果.由图中可以看出,随着图数据集的密度增大,即边的数量增加,近似图覆盖比例逐渐下降.这是由于在高密度的图数据集中,节点对之间的路径较多,其中满足最大伸缩因子的路径数量也较多,因此大量的边均不需保存在近似覆盖子图中,使得覆盖图与原图的边数量比较低. Fig. 5 Coverage ratio on different dataset图5 不同数据集上的覆盖比例 同时由图5中还可以看出,近似图覆盖比例随着聚簇阈值的增大呈U型变化.当聚簇阈值较小时,簇的数量较大,则需保存大量的簇间桥边,同时由于单个簇中节点较少,节点间的簇内连接(包括簇边和自由边)保留比例较高,使得整体覆盖比例较高.当聚簇阈值较大时,大量节点由于无法聚簇而成为自由节点,导致大量的自由边需要保存在近似图覆盖子图中,使得近似图覆盖比例较高.特别是在低密度图数据集中,当聚簇阈值较大,甚至大于图中节点平均度时,只能形成数量极少的簇,此时近似图覆盖比例极高. 现有无向图近似覆盖的研究成果中,最佳聚簇阈值大多设为n1/3,对应本文实验中图数据集的节点数量,则最佳阈值为20.由实验结果可以看到,4个数据集在聚簇阈值为20左右时表现一致,所得近似图覆盖比例均为最低(不同数据集约为 0.001~0.01左右),验证了本文的理论分析,即近似覆盖图中边的数量主要与节点数量相关,这与相关无向图的研究结果也是一致.同时较低的最优覆盖比例也符合真实大规模图的拓扑统计特性,即图中节点平均度不高的同时,节点间的最短路径仍然较短,即所谓的小世界特性.特别是近似覆盖图的节点间路径长度约束较原图更宽,所需边的数量更少,因此所得最优近似图覆盖比例极低,极大的降低了图数据存储的空间开销. 图6所示是平均伸展率随着聚簇阈值的改变表现出的不同情况,图6中4条折线分别表示本文算法在4个不同人工图数据集上运行的结果,其中平均伸展率是采用随机选取10 000对节点计算所得的采样估算值.由图6中可以看出平均伸展率随着聚簇阈值的增大基本呈倒U型变化,与图5中的近似图覆盖比例变化相对应,即近似图中保存的边比例越高,节点间路径越接近原图,平均伸展率越小.当聚簇阈值较小时,较多的簇内与簇间连接使得节点间的路径与原图相比变化较小,因此平均伸展率较小.当聚簇阈值较大时,形成少量的簇与大量自由节点,原图中许多节点间的路径由大量的自由边维持下来,使得平均伸展因子趋近于1.当聚簇阈值为20左右时,近似图覆盖比例最低,而此时平均伸展率较大.由于删除了原图中大量的边,因此很多相邻节点不再保持有直接的邻居关系,而是需要由始点经过若干次转接间接到达终点.图6中实验结果显示,平均伸展因子峰值为3.08,接近定义1给出的理论上限3x+2. Fig. 6 Stretch ratio on different dataset图6 不同数据集上的伸展率 4个数据集的数据曲线趋势基本一致,且随着数据集节点平均度的增加,平均伸展率有所增大.这显然是由于低密度图的近似覆盖比例较高,近似图中保留的边相对更多,使得节点间路径变化更小,这同样与图5所示相对应. Fig. 7 Runtime on different dataset图7 不同数据集上的运行时间 图7所示是算法运行时间随着聚簇阈值的改变表现出的不同情况,图7中4条折线分别表示本文算法在4个不同人工图数据集上运行的结果.由图7中可以明显看出,算法在节点平均度较低的图数据集上运行时间较短,这是因为同样聚簇阈值下,算法在稀疏的图数据集中需要处理的边的数量较少. 同时由图7中还可以看出算法运行时间随着聚簇阈值的增大呈下降趋势.由算法描述可知,较大的时间开销一部分在于Tpre(x)与Tnext(x)这2个集合中边信息的处理,并且需要遍历节点x邻接点所属簇,另一部分在于边端点均为簇节点时,需要判断其所属的多个簇之间的重叠情况,因此簇的数量极大的影响算法时间效率.当聚簇阈值较小时,运行时间较长,随着聚簇阈值增大,簇的数量显著减少,算法运行时间也随之明显缩短,但当聚簇阈值继续增大时,由于所保存边的数量达到最小值后开始增加,运行时间缩短的趋势开始平缓. 本文算法适用于计算有向图的近似覆盖图,而相关研究工作多针对无向图环境,且少有的针对有向图环境的研究,其距离的定义较为特殊,不具有普遍意义,因此算法效率之间直接的定量对比没有明确的意义.直观看来,与相同规模(节点与边的数量相同)的无向图相比,有向图的近似覆盖图中保留的边显然更多,存储开销更大,算法的时间复杂度也更高.本节定性的分析本文算法与同为聚簇方法的无向图环境下近似覆盖图算法相比,空间与时间开销存在差异的原因. 本文算法存储空间的额外需求主要是自由边的增加.为保证同簇内上簇节点之间、下簇节点之间以及下簇节点到上簇节点的连通,在近似覆盖图中保留了许多簇内自由边,这类边在无向图环境下是不需要保存的.尽管随着数据流的到达,在逐步聚簇的过程中删除了其中的冗余,但仍有一部分保留至最终的近似覆盖图,增加了存储开销.类似地为保证簇间节点的连通性,当边的2个端点分别为不同簇的上簇节点,若当前桥边不满足端点间连通的需求,则需要保留簇间自由边,或者当边终点为与始点不同簇的下簇节点时,若当前没有桥边,则也需要保留簇间自由边.簇间自由边类似于额外的桥边,这类边在无向图环境下是也不需要保存的. 时间开销方面,当边到达时,本文算法需要考虑的情况比无向图环境下更为复杂.当边端点均为簇节点时,本文算法需要判断该边是否应保留为簇内自由边、簇间自由边或者桥边,因此要进行多次集合的交与并操作,而无向图仅需判断2个端点是否同簇.当自由边数量超过阈值时从而需要删除其中冗余时,本文算法需要再次判断这些边是否应保留为簇内自由边、簇间自由边或者桥边,而无向图仅需判断端点是否仍是自由节点.聚簇过程中,对于新簇内可能出现的簇内自由边冗余,本文算法需要通过遍历相关上簇节点与下簇节点集删除这部分冗余,而无向图中并不存在簇内自由边,因此不需要进行这部分处理. 由以上分析可以看出,本文算法相比无向图环境下的算法,时空开销均有所增加,但其原因是由于保证有向图节点间连通所带来的复杂性的增加.相对于有向图与无向图之间复杂度的差异,本文算法复杂度的增加十分有限,可以认为其时空效率较佳. 本文以有向图为研究对象,重新定义了近似覆盖图计算过程中所需的相关概念,包括簇集与簇边、桥边、自由边3类关键边,以及由有向图簇衍生出的上簇节点与下簇节点等不同类型的节点.通过理论分析的方式,证明了这3类边的集合满足覆盖因子为(3,2)的有向近似覆盖图的定义.针对图数据以流模式到达的情况,本文给出依次处理每条到达边的具体算法.算法通过判断边端点的类型,据此将到达边抛弃或保存适合类型,并在满足聚簇阈值时形成新簇,最终得到包含簇边、簇间桥边以及自由边的近似覆盖图.算法空间开销的理论分析结果表明,对于包含n个节点的有向图G,其最大化簇集的(3,2)-覆盖包含O(n24)条边.最后,考虑幂指数特性是现实大规模图数据的普遍规律,本文实验数据选取以幂指数模型为基础的人工图数据,通过对比节点平均度不同的图数据,观察随聚簇阈值变化时,算法的空间时间效率等方面的变化.实验结果表明:本文算法在满足覆盖因子约束的前提下,时空效率均较好.3 实验与分析
3.1 实验环境与方法
3.2 实验结果
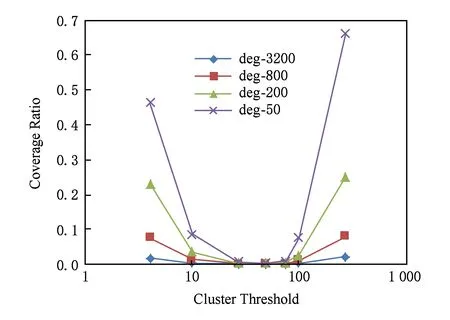
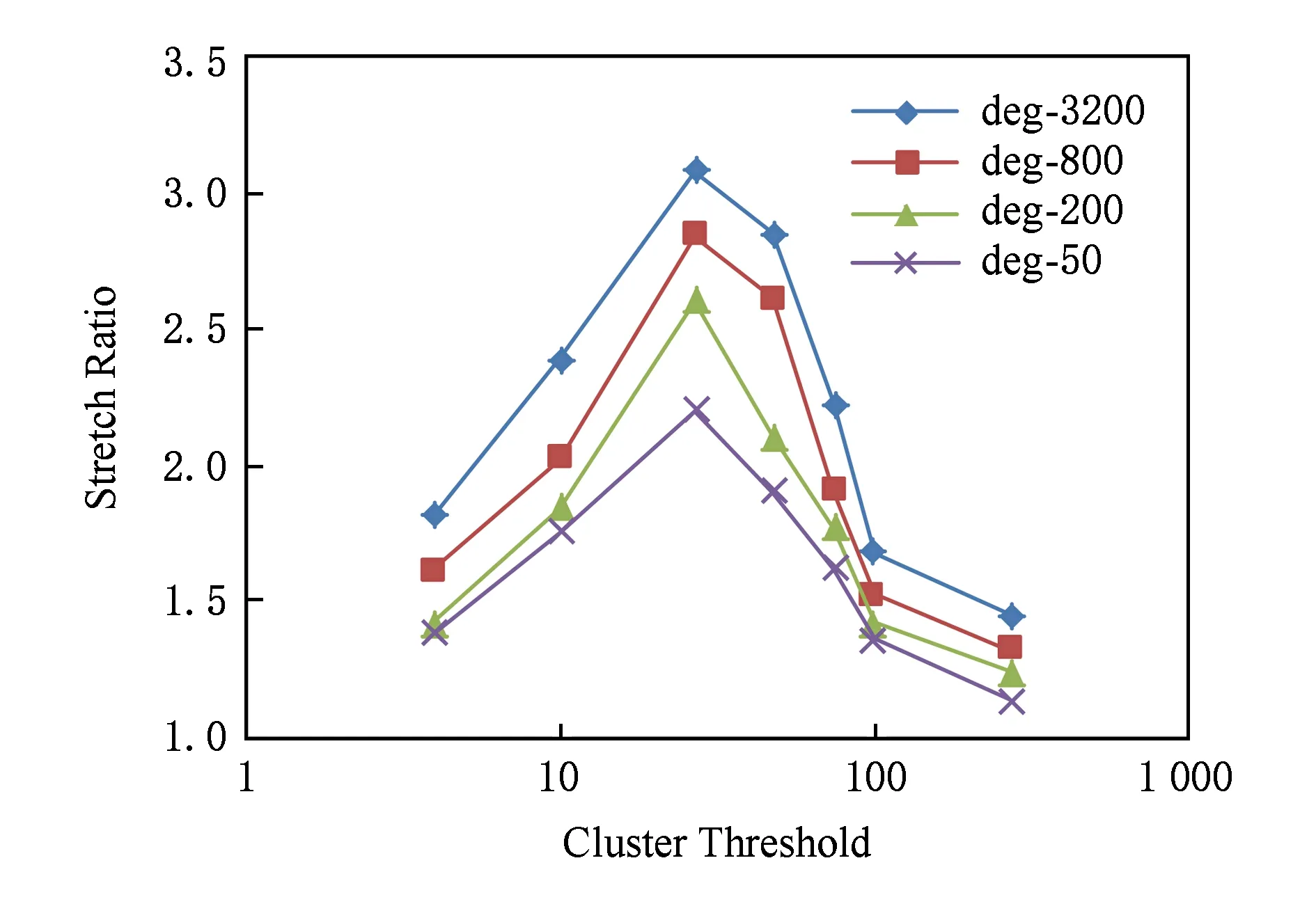
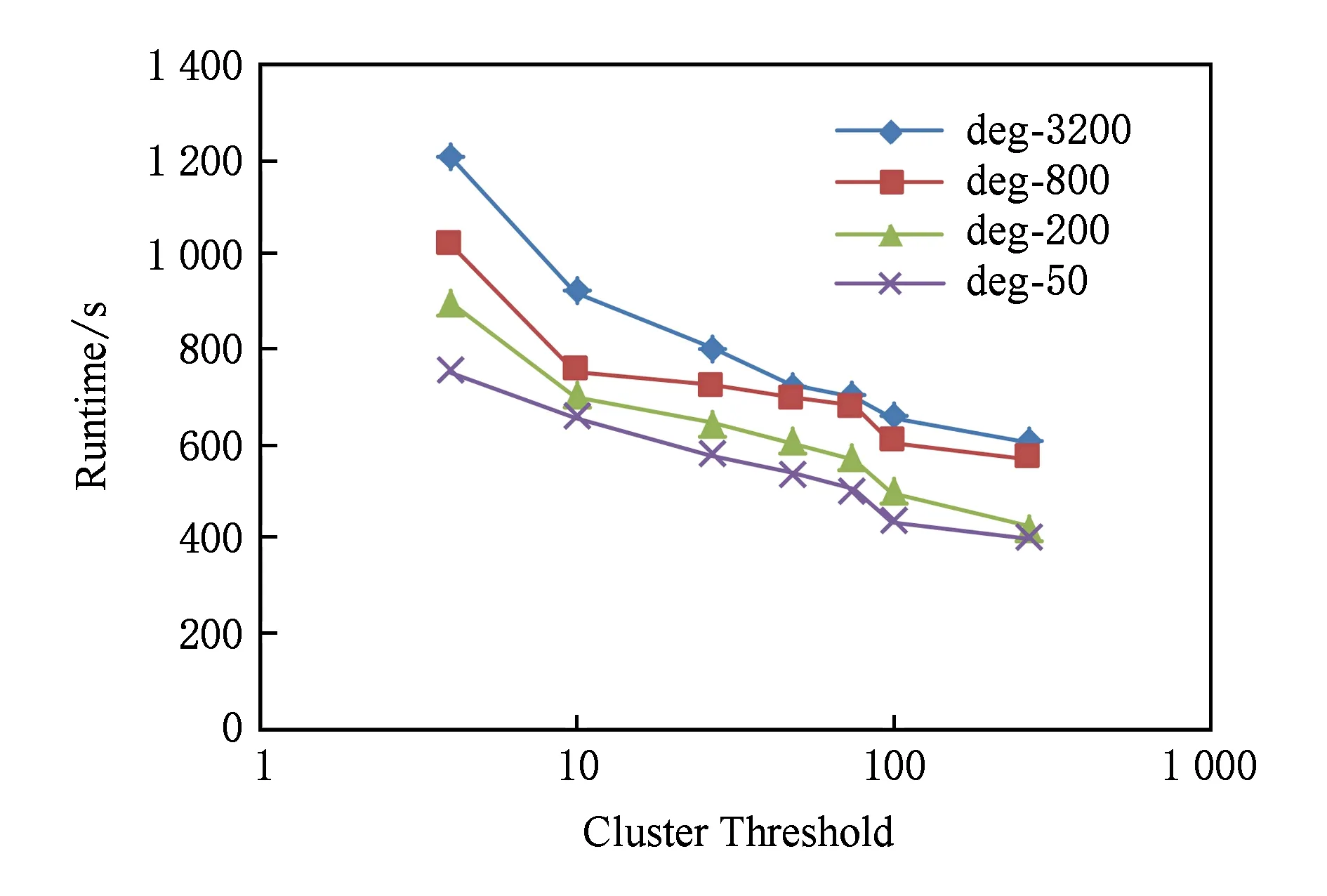
3.3 与无向图的对比分析
4 总 结
