不同干密度下土水特征曲线模型参数确定简化方法

2019-03-20，

长江科学院院报 2019年3期

，

(湖北工业大学土木建筑与环境学院，武汉 430068)

1 研究背景

土体的吸力是由土中各种物理或物理化学反应所产生的，一般认为吸力所反映的是土中水自由能状态，它在研究非饱和土的强度方面有十分重要的地位。SWCC(土水特征曲线)是用于描述土体中的吸力与含水量之间的本构关系函数曲线，SWCC对于研究非饱和土的物理力学特性占着举足轻重的位置。根据SWCC可以得到非饱和土的强度、渗透系数、体积变化量，因此对于SWCC的研究一直是非饱和土方面的热点问题[1]。

近年来许多学者对土水特征曲线与土体特性之间的关系进行了大量研究。王晓峰等[2]在将土水特征曲线大致划分为4个阶段的基础上进行了大量数据统计分析，由此建立了一种简化分段模型，以得到非饱和土渗透曲线。常波等[3]对巴东黄土坡滑坡土的非饱和性质进行研究，进行了土水特征曲线和变水头试验，得出滑带土在不同基质吸力下对应含水量与渗透系数，并对土水特征曲线和渗透曲线进行拟合。Vanapalli等[4]通过引入“等效压力”的概念，研究了在不同竖向压力和初始含水量条件下的冰碛土土水特征曲线。褚峰等[5]通过非饱和土固结仪研究了在不同初始干密度、不同含水率条件下竖向应力对非饱和黄土土水特征曲线的影响，发现竖向应力对非饱和黄土土水特征曲线的影响较小，并提出了黄土土水特征曲线经验表达式。张雪东等[6]通过引用孔隙尺寸分布函数，建立了一个能模拟孔隙率对土水特征曲线影响的经验模型。

本文研究对象为非饱和粉质黏土，通过测定其不同干密度下土水特征曲线并使用3种常用土水特征曲线模型进行拟合，探究了不同干密度下模型参数的变化规律，避免了为获得模型参数的复杂测试过程，具有一定的实用性，期望能为工程提供参考。

2 土水特征曲线试验

取武汉某基坑底部非饱和粉质黏土进行土水特征曲线试验，取土深度为9 m，土粒相对密度为2.75，天然密度2.03 g/cm3，天然含水量21.9%，液塑限分别为38.9%和20.4%。土样烘干后磨成粉过2 mm筛，通过静压法制得干密度分别为1.30，1.35，1.40，1.45，1.50，1.60，1.71 g/cm37个试样，对试样饱和后进行压力板仪试验获得各试样土水特征曲线[7]，各干密度试样土水特征曲线如图1所示。

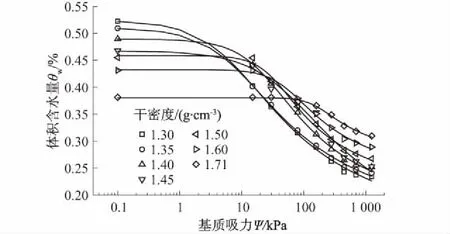
图1 不同干密度下试样土水特征曲线Fig.1 SWCCs of clay samples with different dry densities

3 土水特征曲线模型拟合分析

目前，可用于描述土水特征曲线常用的模型有：Gardner模型、Brook and Corey模型、Van Genuchten模型和Fredlund & Xing模型等。这些模型一般拟合程度均较好，模型中参数采用数理统计的方式求出。

本文仅用Gardner[8]，Van Genuchten[9]，Fredlund & Xing[10]3种模型对不同干密度试样土水特征曲线试验数据进行拟合，并对模型中特征参数的变化规律进行探讨。各模型表达式和模型参数如表1，其中：θs,θr分别为试样饱和含水率和残余含水率；b,p,α,m,n均为拟合参数；ψ为基质吸力；ψr为残余含水量状态时的吸力；在Van Genuchten模型中有m=1-1/n。

表1 SWCC 模型表达式及参数Table 1 SWCC models and parameters

表2、表3、表4分别为3种模型的似合参数。

表2 不同干密度试样Gardner模型拟合参数Table 2 Fitting parameters of SWCC of soil sampleswith different dry densities by Gardner

注：SSE为残差平方和，R2为决定系数

表3 不同干密度试样Van Genuchten模型拟合参数Table 3 Fitting parameters of SWCC of soil sampleswith different dry densities by Van Genuchten

表4 不同干密度试样Fredlund & Xing模型拟合参数Table 4 Fitting parameters of SWCC of soil sampleswith different dry densities by Fredlund & Xing

通过比较表2—表4中3种模型的拟合程度可知，3种模型相关系数除干密度为1.50，1.60，1.71 g/cm3时Gardner模型R2为0.940，0.949，0.953，其他决定系数均超过了0.96，相关程度很高。Van Genuchten模型中参数α是与进气值和孔径分布相关的参数，由表3可知随干密度的增加，参数α逐渐减小，从参数α的变化趋势可以间接了解到干密度越大试样的进气值越大，孔径分布越均匀，土水特征曲线曲线拐点后斜率逐渐变小。从土水特征曲线的斜率可以看出试样的持水能力，斜率越小持水能力越好[11]，试样的水稳定性随干密度的增加而增强。饱和含水量θs与干密度线性正相关，通过计算决定系数超过0.98，饱和含水量受干密度影响明显。在Fredlund & Xing模型中与参数α所相关的试样参数与Van Genuchten模型中一致，在表4中参数α的变化规律所代表的土样性质变化规律也与Van Genuchten模型中一致，参数m没有与之特定相关的试样参数。值得注意的一点是当试样干密度发生改变时使用Fredlund & Xing模型拟合出的饱和含水率θs不随着干密度的增加而减小，这与实际不符。

4 模型参数确定方法

土水特征曲线试验过程中首先要对试样进行饱和，因此可认为在土水特征曲线试验过程中水的体积就是试样中孔隙体积，且由基质吸力和土体中等效孔径成反比可知土水特征曲线实际上反映了土中孔隙分布情况，干密度与孔隙比之间有着密切的联系，可以在一定程度上表征试样的孔隙分布情况。笔者在研究过程中将干密度和Gardner模型、Van Genuchten模型和Fredlund & Xing模型中的模型参数放在一起进行分析并通过最小二乘法拟合，可得图2—图4。

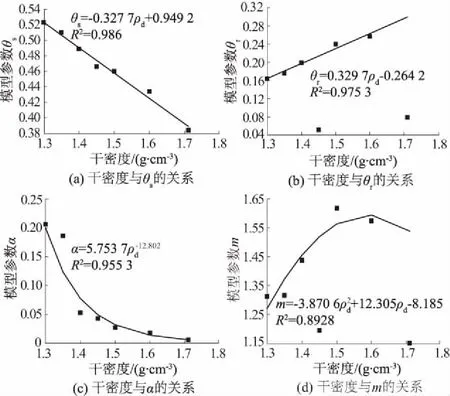
图3 干密度与Van Genuchten模型参数θs，θr，α，m之间的关系Fig.3 Relationship between dry density and parameters of Van Genuchten’s model

图4 干密度与Fredlund & Xing模型参数α，m，n，θs之间的关系Fig.4 Relationship between dry density and parameters of Fredlund & Xing’s model

从图2—图4中可以看出，当去除Van Genuchten模型参数θr，m中与干密度离散性较大的点后，Gardner和Van Genuchten模型参数与干密度的相关性较好，R2均超过0.88。Fredlund & Xing模型参数θs，m与干密度之间关系的离散性很大，相关性很低。因此，不再讨论Fredlund & Xing模型。Gardner模型参数与干密度之间关系式为：

θs=-0.492ρd+1.223 6 ;

(1)

b=30 127e-8.997 3ρd;

(2)

(3)

Van Genuchten模型参数与干密度之间的关系式为：

θs=-0.327 7ρd+0.949 2 ;

(4)

θr=0.329 7ρd-0.264 2 ;

(5)

(6)

(7)

将式(1)—式(7)分别代入Gardner和Van Genuchten模型中可得：

θw=(-0.329 7ρd+0.949 2)+(-0.657 4ρd+

1.213 4)/{[1+(5.753 7ρd-12.802·

(9)

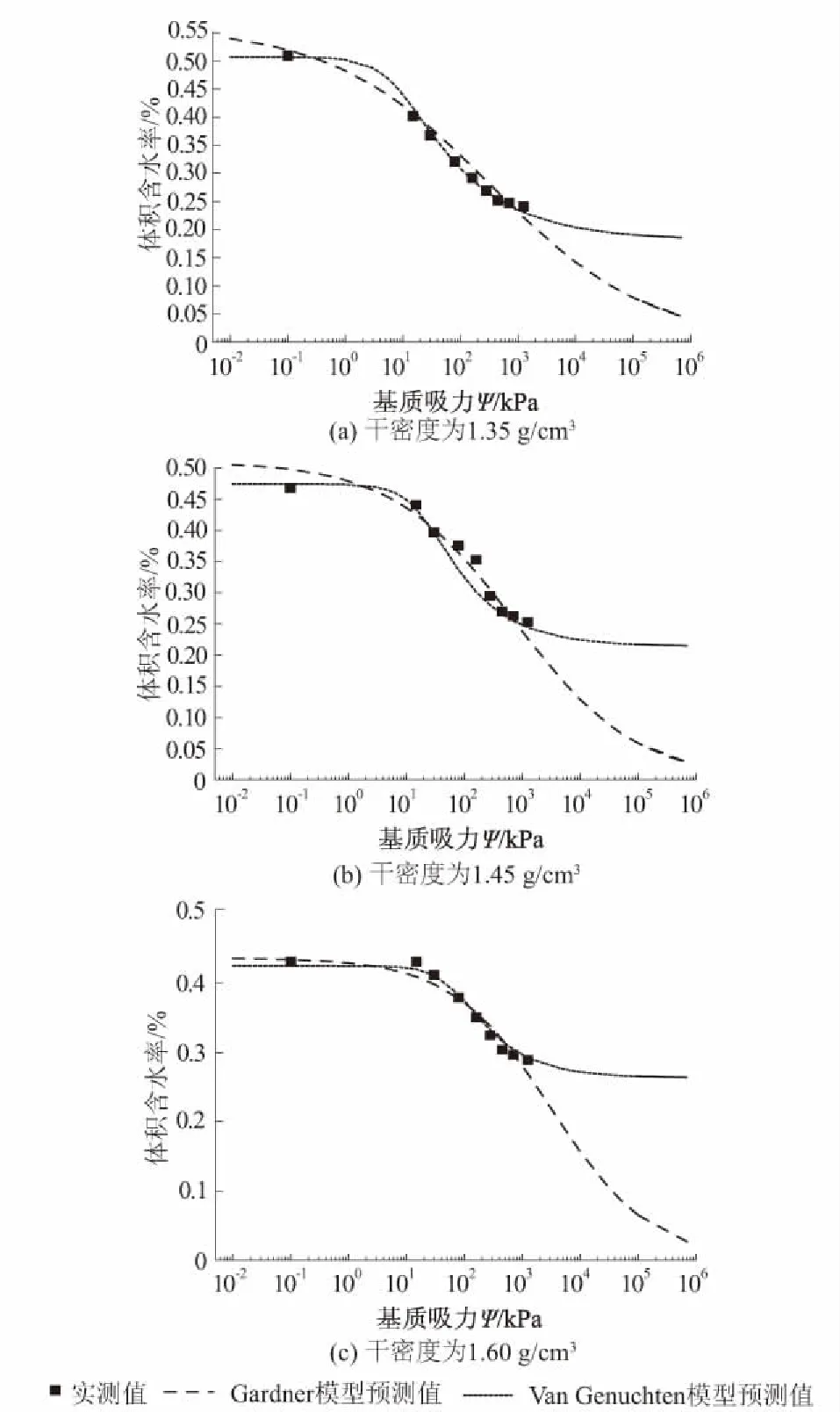
图5 不同干密度时土水特征曲线实际值与预测值对比Fig.5 Measured and forecast SWCCs of soil samples with different dry densities

使用式(8)、式(9)理论上可以预测任意干密度下土样的土水特征曲线。为了验证本文结论，使用式(8)、式(9)预测干密度分别为1.35，1.45，1.60 g/cm3时土水特征曲线，实测值与预测值如图5所示。经计算可知使用式(8)、式(9)预测干密度1.35，1.45，1.60 g/cm3土水特征曲线决定系数分别为0.968，0.948，0.944和0.993 8，0.909 3，0.981 9，验证了本文结论的适用性。

5 相关讨论

(1) 对于Van Genuchten模型，进行参数θr和m拟合时在干密度1.45 g/cm3和1.71 g/cm3处出现了离散性很大的2点，当去掉这2点后模型参数与干密度之间相关性良好。通过本文方法预测干密度分别为1.35，1.45，1.60 g/cm3的土水特征曲线时，相关系数分别为0.993 8，0.909 3，0.981 9。可以发现在预测干密度为1.45 g/cm3的土水特征曲线时虽然相关系数超过了0.9，但和其他2个干密度的决定系数0.993 8和0.981 9相比出现了骤降，出现该现象的原因可能是试验误差、模型自身因素，能否根据本文方法提出可以提高预测模型相关系数的修正方法值得继续研究。

(2)在使用Gardner模型进行模型参数与干密度之间相关性分析后，再使用本文方法进行土水特征曲线预测时拟合效果较好，均取得了较高的相关系数。但文献[12]发现本文中模型参数p与干密度的离散性很大，未发现良好的拟合函数，文献[12]中研究土样为黄土，出现这种现象的原因可能是土的类型不同、制样或取土方法的差异导致土体内结构不同、土体内部所含矿物质不同。若是土的类型或土中所含矿物不同导致这种现象，可以将模型分类根据适用的不同类型土建议模型；若是制样或取土方法导致这种现象应规范试验中制样或取土方法。