基于MF-DFA法和PSO-ELM模型的基坑变形规律研究

2019-03-20

长江科学院院报 2019年3期

(石家庄职业技术学院，石家庄 050000)

1 研究背景

伴随城市建设的快速发展，高层建筑日益增多，与之相关的基坑工程不断增加[1]。在基坑开挖过程中，变形监测可有效反映支护结构的稳定状态，对及时发现施工安全隐患具有重要的作用。但结合工程实际，监测成果的反馈往往具有滞后性，加之监测项目多、环境因素影响大等特点，有必要对基坑的变形趋势分析及预测进行深入研究，以便为基坑施工过程中的安全评价提供一定的参考。

目前，已有许多学者对基坑的变形预测进行了研究，如李莉等[2]利用3种优化方法对GM(1,1)模型进行优化，构建了二次优化的灰色模型，结果显示该模型的预测精度较高，工程应用价值较好；刘贺等[3]构建了粒子群优化的神经网络模型，并对基坑变形进行预测，得出该模型能实现基坑变形的有效预测，预测结果具有较高的可信度；张运良等[4]通过基坑变形的数值模拟，总结出了各种支护条件下的基坑变形规律，为支护结构设计及基坑开挖等提供了一定的依据。上述研究虽取得了相应的成果，但均是基于基坑累计变形序列的研究，缺少通过变形速率序列来预测基坑变形趋势的研究，也缺少多重分形去趋势波动分析(Multifractal Detrended Fluctuation Analysis，简称MF-DFA)法和极限学习机在基坑变形研究中的应用。其中，多重分形去趋势波动分析法是一种能定量分析非线性复杂序列的研究方法，被广泛应用于自然生命科学、水文等多个领域[5]，如袁晓辉等[6]利用改进MF-DFA法对长江流域某水文站的径流序列进行预测，揭示了该站径流序列的多重分形特征；于伟红等[7]通过MF-DFA法分析了河北省近56 a的降水和气温变化趋势，对分析区域气候变化特征具有重要的意义。同时，极限学习机已在岩土领域得以应用，主要用于累计变形序列的变形预测，如高彩云等[8-9]将其应用于地铁隧道沉降及滑坡变形预测中，经实例检验该模型具有较高的预测精度，且预测结果的稳定性较好。

因此，本文拟从累计变形序列和变形速率序列2方面入手，先利用MF-DFA法对基坑变形速率序列进行多重分形分析，以判断基坑的变形趋势；再利用极限学习机对基坑的累计变形序列进行预测，以实现基坑的变形预测；最后，对比两者分析结果的一致性，实现从累计变形序列和变形速率序列2方面来综合评价基坑变形的综合特征，以期为基坑支护结构的稳定性评价提供一定的依据。

2 基本原理

2.1 MF-DFA法

MF-DFA法能有效评价非稳时间序列的多重分形特征，且能对评价序列的发展趋势进行有效判断，因此，利用该方法对基坑速率变形序列进行检验分析，其计算步骤如下[10-11]。

(1)若基坑的变形速率序列为{xi}(i=1,2,…,N)，则可求得该序列的累计离差序列{yi}为

(1)

式中x′为速率序列的平均值。

(2)将yi划分为等长度s的若干区间，则区间个数为Ns=N/s(取整数)。但在划分过程中，由于序列长度N并非总是长度s的整数倍，在Ns取整数时，序列后部分的相关节点将不能发挥作用，因此，再逆序进行相同区间长度s的划分，即在区间长度s条件下，共计有2Ns个子区间。

(3)计算均方根误差F2(s,v)(v=1,2,…,2Ns)。对确定v值条件下进行k阶多项式拟合，即

yv(i)=a1ik+a2ik-1+…+ak+1。

(2)

当v∈{1,2,…,Ns}时，均方根误差为

当v∈{Ns+1,Ns+2,…,2Ns}时，均方根误差为

F2(s,v)=

(4)

(4)计算q阶对应的波动函数，即

(5)

式中：F(q,s)与s为幂函数关系；q为非0实数。

(5)计算广义Hurst指数。在特定s值条件下，求得相应的F(q,s)，进而得到若干散点(s，F(q,s))，且各散点间存在线性关系，因此，通过对所有散点的线性拟合求得广义Hurst指数h(q)，即

lnF(q,s)=lnk+h(q)lns。

(6)

(6)求解奇异指数a。奇异指数可以描述评价序列的奇异程度，其最大、最小的差值可描述分形谱的宽度，两者的计算公式分别为：

a(q)=h(q)+qh′(q) ；

(7)

Δa=amax-amin。

(8)

通过上述参数计算，当h(q)的值不依赖于q值时，即h(q)始终保持一个常数时，评价序列不具有分形特征；但当h(q)的值随q的增大而减小时，则说明评价序列具有多重分形特征，且Δa值越大时，评价序列的分布越不均匀，且分形特征越显著。同时，通过h(q)值可以对评价序列的长期相关性和变形趋势进行判断，即：

当h(q)=0.5时，评价序列表现为随机游走的性质，不能对其发展趋势进行评价。

当h(q)>0.5时，评价序列具有长期相关性和持久性，能对序列的发展趋势进行评价，即评价序列将保持与前一阶段相同的变形趋势，且偏离0.5的程度越大，趋势性越明显。

当h(q)<0.5时，评价序列具有长期相关性和反持久性，也能对序列的发展趋势进行评价，即评价序列将保持与前一阶段相反的变形趋势，且偏离0.5的程度越大，趋势性越明显。

2.2 极限学习机

极限学习机(Extreme Learning Machine，ELM)是一种前馈神经网络，具有3层网络结构，较传统神经网络具有简单易用、泛化性好、学习速度快、参数设定简单等优点。若有n个分析样本(xi,ti)，i=1,2,…,n,其具有M个隐层节点的极限学习机形式为[12-13]

(9)

式中：g(x)为激励函数；wi为第i个隐层节点与输入层节点间的权值向量，即wi=(w1i,w2i,…,wMi)；βi为第i个隐层节点与输出层节点间的权值向量，即βi=(β1i,β2i,…,βMi)T；oj为输出向量，即oj=(oj1,oj2,…,ojn)T;bi为隐层神经元的偏置向量。

同时，存在βi，wi，bi使预测结果零误差地逼近训练样本，即

(10)

式(10)可进一步转化为

Y=Hβ。

(11)

式中：Y为预测样本矩阵；H为常数矩阵，且通过对式(11)进行最小范数的最小二乘求解，计算过程为

β=H+Y。

(12)

式中H+为H的摩尔-彭罗斯广义矩阵。

从研究清代碑帖融合代表角度肯定清代帖学影响力的文章相对较多，主要围绕吴德旋、何绍基、赵之谦、沈曾植等展开。

同时，虽然极限学习机具有较好的预测性能，但其连接权值、隐层节点数等对预测精度也有较大的影响，如输入权值矩阵与隐层间的偏差可能出现为0的状况，导致隐层节点无效。因此，在极限学习机的应用过程中，需要较多的隐层节点才能达到预期的效果，从而增加了网络的复杂度，导致过拟合现象的产生。为解决该问题，将粒子群优化算法引入到极限学习机的参数优化过程中，构建PSO-ELM模型，以期提高预测精度，且优化过程已在文献[14]中详述，不再赘述。

2.3 数据预处理

结合工程实际，受环境及施工因素的影响，监测数据往往具有非等距特征，且据MF-DFA法的基本原理，样本数较少时，分析结果的准确性会降低。因此，有必要对原始数据进行预处理，该文提出以3次样条插值对原始监测数据进行拟合，再将其划分为若干等距区间，以实现监测数据非等距到等距的变化。

3 实例分析

为验证该文分析思路的有效性，共采用2个实例进行验证。其中，实例1共分析3个监测点的变形数据，以对比同等地质环境条件下分析模型的有效性；同时，实例2则为验证实例，主要用于验证和探讨分析模型的可推广性。

3.1 工程概况

实例1为某购物中心基坑[15]，拟建3层地下工程，结构形式为混凝土框架结构，且基坑埋置深度为16.27 m，局部10.42 m，采用“护坡桩+预应力锚索+土钉墙”的支护方式。同时，该基坑的近接建筑较为复杂且重要性较高，西侧紧邻一商混站，距离31 m，而北侧紧邻一变电站，据设计单位报告，该基坑的侧壁安全等级为一级，局部为二级。

基坑施工区域及施工深度范围内均为土层，主要为人工填土、粉土、粉细砂及粉质黏土等。对土层的基本特征参数进行统计，如表1所示。

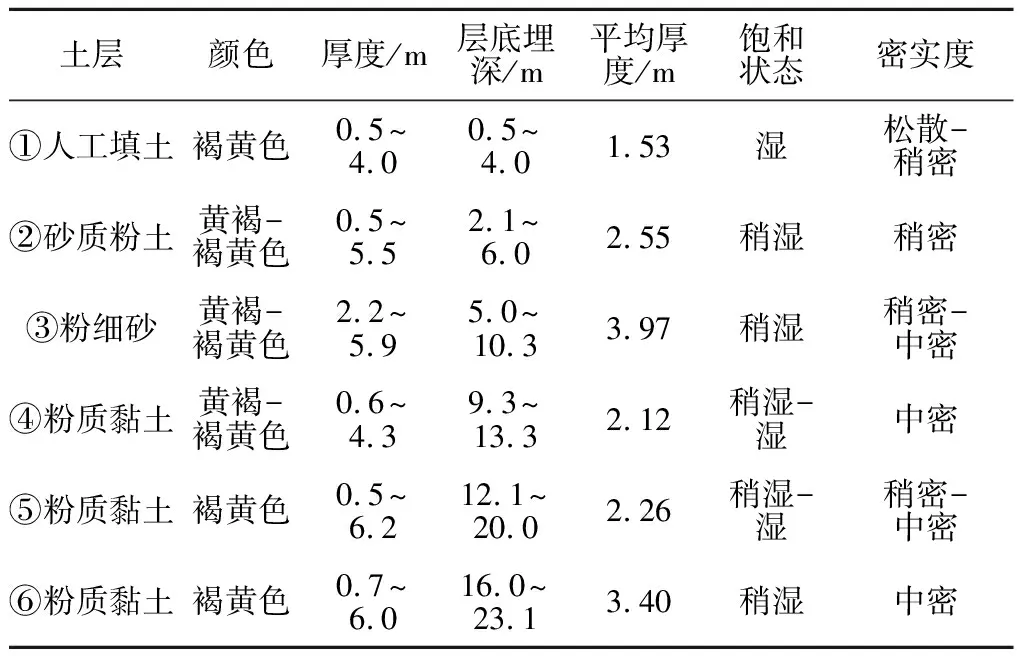
表1 土层基本特征参数统计Table 1 Statistics of basic characteristics of soil strata

为掌握基坑的变形情况，在施工过程中，对基坑进行变形监测，其中，沉降监测点位于基坑周边，采用特制加工的测钉，冲击钻打孔，由水泥和环氧树脂胶水混合后封闭。根据对监测成果的整理，得到1-1监测点、1-5监测点和1-9监测点在经3次样条插值处理后的结果如图1所示，监测时间共计278 d，将其划分为80个周期，每个周期3.519 d。

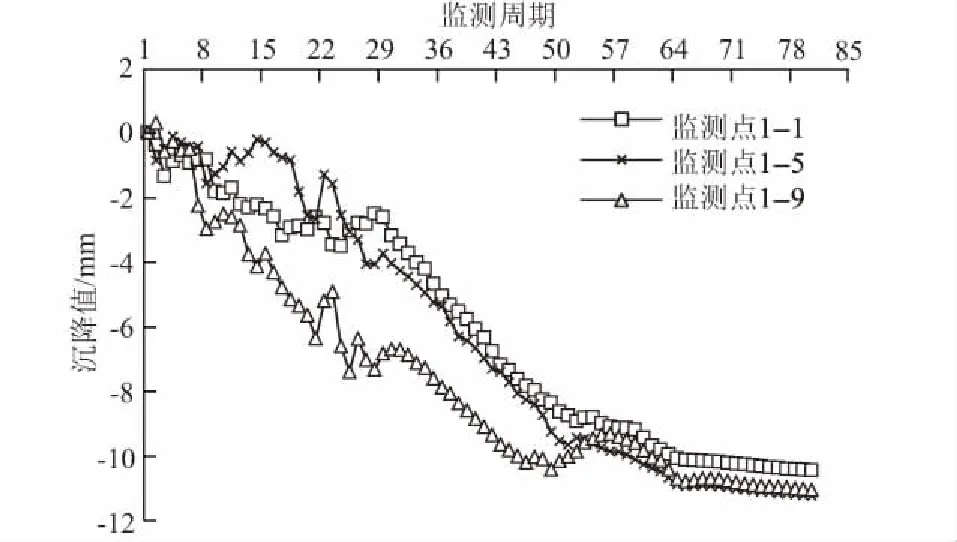
图1 实例1基坑沉降变形曲线Fig.1 Curves of settlement deformation of foundation pit in example 1

3.2 变形趋势判断

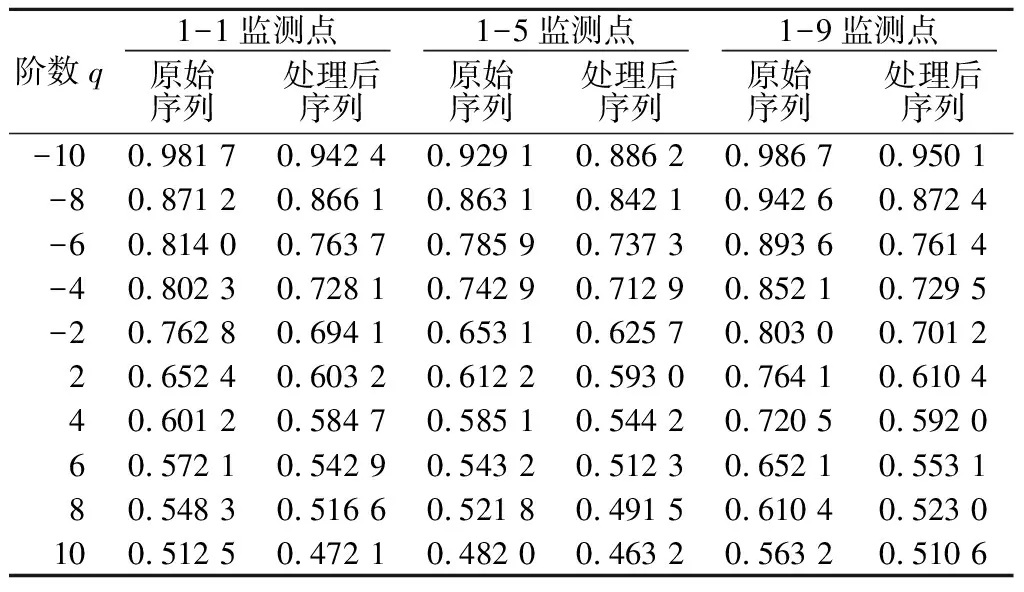
表2 实例1基于MF-DFA法的广义Hurst指数结果统计Table 2 Statistical result of Hurst index of MF-DFAanalysis for example 1

由表2可知，各监测点的广义Hurst指数均表现为随q值增加而减小，说明各监测点的变形速率序列均具有多重分形特征；各监测点的Hurst指数基本都>0.5，且h(2)是标准Hurst指数，均>0.5，说明各监测点的变形速率序列的发展趋势与前一阶段的变形趋势相同，均趋于减小，但变形量仍会持续增加；经去相关性处理后，各节点在相应阶数q条件下的Hurst指数均出现了不同程度的减小，说明各监测点的变形速率序列节点间确实存在相关性，且在去除相关性后，会减弱序列变形的趋势性。

同时，再对各节点的奇异指数进行求解，以对比各节点的分形程度，结果如表3所示。各监测点经去相关性处理后，分形程度均出现了不同程度的减弱，说明评价序列节点间的相关性能增加序列变形的趋势性；各节点的分形程度均相当，1-9监测点的分形程度相对最大，其次是1-1监测点和1-5监测点；各监测点的拟合度均较为接近1，说明各监测点的拟合效果均较好，所得结果的可信度较高。

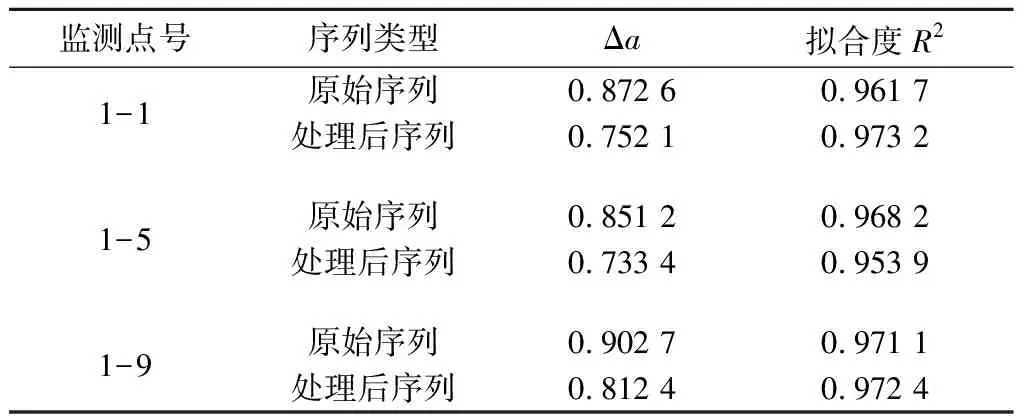
表3 实例1各节点的分形程度评价Table 3 Evaluation of the fractal degree of each nodein example 1

3.3 变形预测分析

为进一步分析基坑的变形规律，再利用极限学习机对基坑的累计变形序列进行预测，其验证周期为第61—第65周期，外推预测周期为第66—第68周期，且为验证粒子群算法的优化效果，先以1-1监测点为例，对优化前后均进行预测，结果如表4所示。

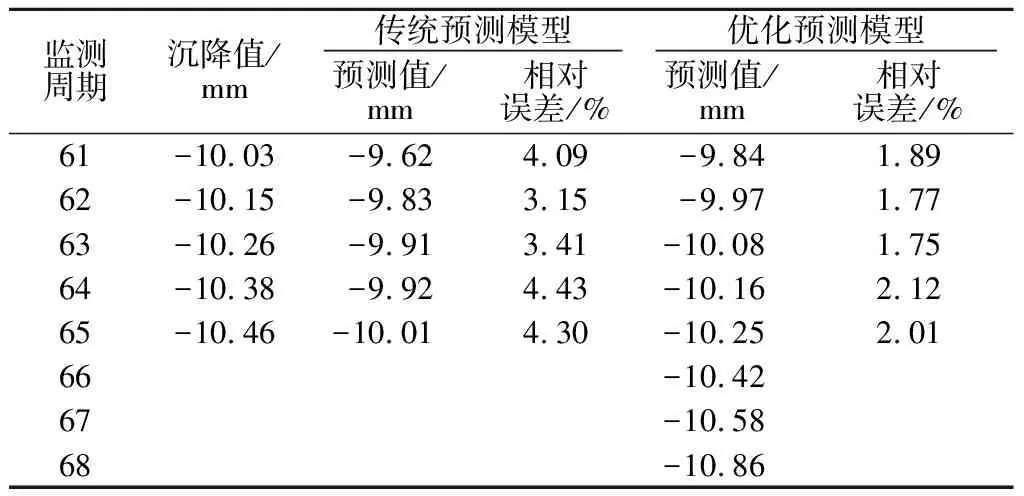
表4 1-1监测点变形预测结果统计Table 4 Statistics of deformation prediction result formonitoring point 1-1

由表4可知，在相应预测节点处，优化模型的预测精度均高于传统模型的预测精度，说明粒子群算法能有效提高预测精度，优化效果较好；在PSO-ELM模型的预测结果中，变形相对误差均<3%，最大相对误差为2.12%，预测精度较高，验证了该模型的有效性。且外推预测结果显示，该监测点的沉降变形仍将持续，但增长幅度趋于减小，与MF-DFA分析结果一致。

通过上述对比，验证了PSO-ELM模型的有效性，因此，再采用该模型对1-5监测点和1-9监测点的累计变形序列进行预测，结果如表5所示。由表5可知，两监测点变形的相对误差均<3%，其中，1-5监测点的最大相对误差为2.24%，1-9监测点的最大相对误差为2.86%，得出两监测点的变形预测精度均较好，进一步验证了PSO-ELM模型的预测精度较好；通过外推预测，两监测点的沉降仍将持续增加，但增加速率趋于减小，也与MF-DFA分析结果一致。

表5 1-5监测点和1-9监测点的变形预测结果统计Table 5 Statistics of deformation prediction result formonitoring points 1-5 and 1-9

综上所述，得出MF-DFA分析结果与预测结果间的一致性较好，相互验证了2种方法在基坑变形规律研究中的有效性和实用性，能对基坑变形趋势进行有效判断。

3.4 有效性检验

为进一步验证该文分析思路的可推广性，再引入实例2进行有效性检验。

3.4.1 工程概况

某泵房基坑[16]长32.75 m，宽15.2 m，东侧开挖深度8 m，西侧开挖深度6 m，且其周边环境条件较为复杂。东南角邻近一办公楼，近接距离为3 m，楼层高为5层；北侧紧邻一多层住宅，近接距离为5 m，且基坑围护桩内侧埋设有一条高压电缆；西侧紧邻浦头港，近接距离为10 m。鉴于基坑周边环境的复杂性，施工现场布设了变形监测点，监测日期为8月6日—10月14日，且监测数据也具有非等距特征，因此，对监测数据进行预处理，并将其等分为40个监测周期，每个周期长度为1.769 d，处理后的变形曲线如图2所示。

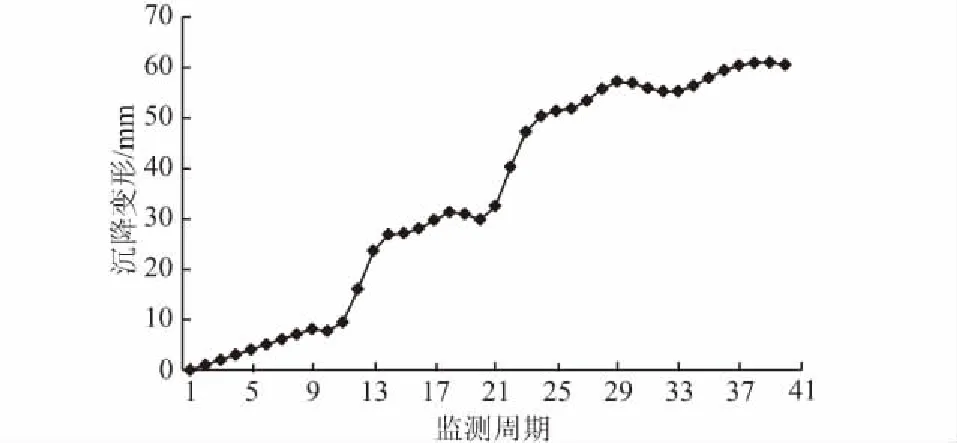
图2 实例2基坑沉降变形曲线Fig.2 Curve of settlement deformation of foundationpit in example 2

3.4.2 变形趋势判断

类比实例1的分析过程，也采用MF-DFA法对实例2的变形速率序列进行多重分形分析，以判断其变形趋势，结果如表6所示。

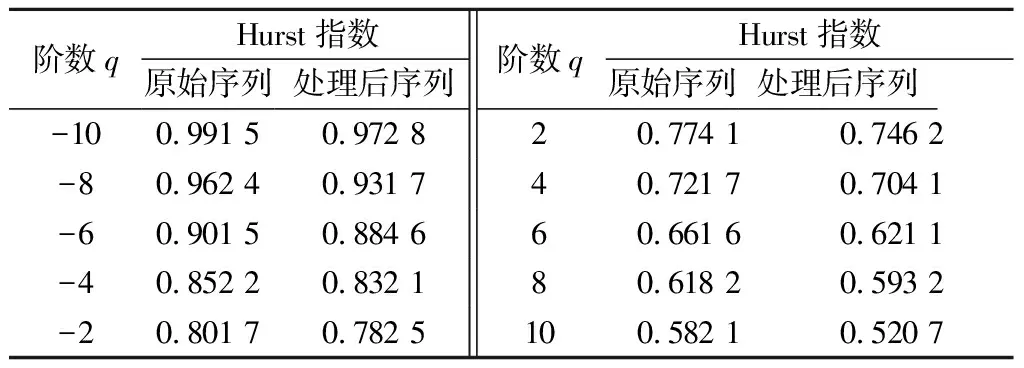
表6 实例2基于MF-DFA法的广义Hurst指数结果统计Table 6 Statistical result of Hurst index of MF-DFAanalysis for example 2

由表6可知，随阶数q的增加，h(q)值也在不断减小，说明实例2的变形速率序列也具有多重分形特征，且各阶数的h(q)值均>0.5，说明该序列具有持久性，其发展趋势与前一阶段相同，将会趋于减小；经去相关性处理后，相应阶数处的h(q)值也出现了不同程度的减小，且分形程度也有所降低，进一步说明序列相关性会增加序列变形的趋势性，但对变形趋势的方向判断没有影响，该序列仍是正向变形趋势。表7显示该序列在处理前后的拟合度均较趋近于1，说明拟合效果较好，所得结果真实可靠。

3.4.3 变形预测分析

再利用极限学习机对实例2的累计变形序列进行预测分析，结果如表8所示。

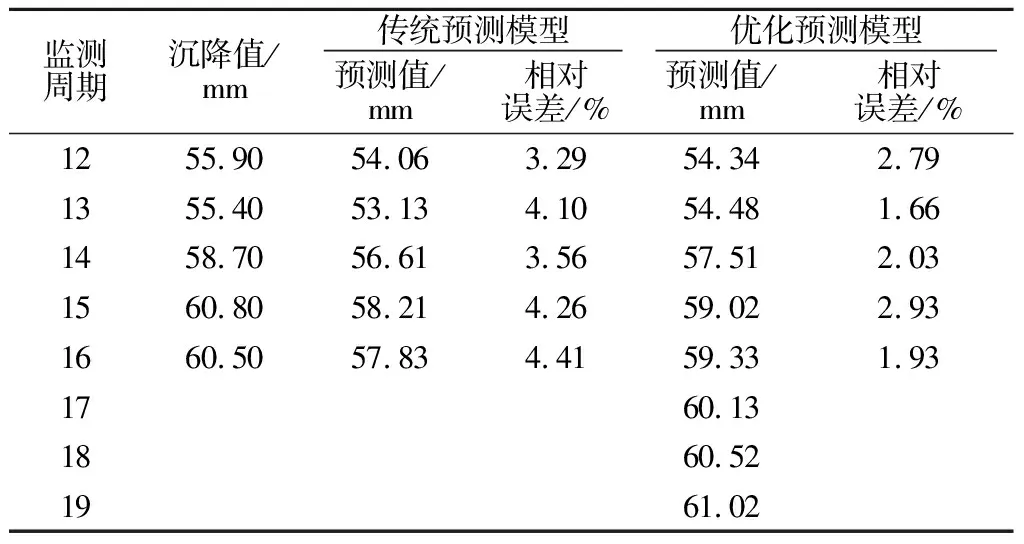
表8 实例2的变形预测结果统计Table 8 Statistics of deformation prediction results forexample 2

对比优化前后相应节点处的预测结果，得出通过粒子群算法的优化，预测精度明显提高，进一步验证了粒子群算法的优化效果；在优化预测模型的预测结果中，最大相对误差为2.93%，最小相对误差仅为1.66%，得出该预测模型的预测精度较高；通过外推预测，得出实例2的基坑变形仍在持续增加，但增长速率趋于减小，与变形速率序列的发展趋势分析一致。

综合2个实例的检验，得出MF-DFA法和极限学习机能准确判断基坑的变形趋势，有效性和可推广性均较好，为2种方法在基坑工程中的应用积累了经验。