GRS结构与MSE结构的性能差异及评价方法

2019-03-20，

长江科学院院报 2019年3期

，

(同济大学土木工程学院地下建筑与工程系，上海 200092)

1 研究背景

GRS(Geosynthetic Reinforced Soil)结构是指加筋间距不超过30 cm、填料压实度超过95%的加筋土体，主要作为加筋桥台等承受上部荷载作用的土工结构物使用[1]。MSE(Mechanically Stabilized Earth)结构则是加筋间距相对较大的加筋土体，即目前工程中常用的加筋土结构，以用作加筋土挡墙或边坡为主，偶尔也用于加筋土桥台。由于GRS结构的加筋间距更小，且填料压实效果更好，一般认为GRS结构具有承载能力更好、沉降及侧向位移更小、墙面所受的侧向土压力更小、筋材应变及受力更小等优于MSE结构的特性[2-3]。

GRS结构与MSE结构的本质区别在于受力机制的不同。一般学者认为：MSE结构的受力机制是“力的传递与平衡”，即潜在破裂面外侧不稳定土体的侧向土压力由面层系统承受，并通过与面层连接的筋材将该部分土压力传递至筋材锚固段的稳定土体中，以达到力的平衡[4-5]。GRS结构虽然是MSE结构的改进，但在受力机制上却表现出质的变化，通常被视为一种类似于“钢筋混凝土”的具有复合材料特性的复合体结构[6-7]。受力机制的不同，导致了GRS结构和MSE结构之间结构性能的差异。

关于GRS结构和MSE结构的性能特点及其影响因素方面的试验研究，目前已有不少的成果积累。在承载力特性方面，Adams等[8-9]利用实际工程材料进行了一系列小型桥墩的承载性能试验(MP试验)，结果表明GRS结构的极限承载力通常能达到1 000 kPa以上；Wu等[10]通过现场试验得到的GRS桥台的极限承载力则略低。Nicks等[11]进一步研究了GRS结构承载特性的影响因素，结果表明：填料力学性质越好、压实度越高、筋材强度越大、加筋间距越小，承载能力越好。Wu等[12]通过平面应变条件下的土-筋复合体试验(GSGC试验)对比了GRS结构和MSE结构之间承载性能的差异，结果表明GRS结构的极限承载力要比MSE结构大很多。在变形特性方面，美国联邦公路管理局(FHWA)总结了一些GRS桥台的沉降监测数据，认为GRS桥台的压缩变形基本上在施工阶段完成，通车后的沉降及差异沉降均很小[8]。美国特纳-费尔班克公路研究中心(TFHRC)对采用不同筋材强度的2座GRS桥台进行了长达12 a的沉降监测，结果表明筋材强度对GRS结构变形的影响不大[13]。Bueno等[14]和Benjamim等[15]总结了部分GRS结构的工程监测数据，认为GRS结构在自重荷载条件下的最大侧向位移及筋材最大应变基本发生在结构高度的中心位置附近；而MSE结构的最大侧向位移一般认为发生在结构高度的2/3处。Adams等[8]通过工程经验的总结，认为压实性良好的加筋土结构的侧向变形与竖向变形之间近似满足“体积应变为0”的关系，并给出了经验换算公式；Khosrojerdi等[16]利用室内模型试验的数据进一步验证了这一结论。

尽管对于GRS结构和MSE结构单独展开的试验研究已有了丰富的成果，但在同一批次的试验中直接对比研究两者在工作荷载状态下的性能差异的成果还很少见。本文根据相似理论，设计了收缩比例为1/2的缩尺模型试验进行GRS结构和MSE结构在工作状态下的性能特点的对比研究。实际工程中，GRS结构的常用加筋间距为0.2 m或0.3 m[12]，MSE结构的典型加筋间距为0.6 m[17]，因此试验中根据收缩比例1/2分别设置0.1，0.15，0.3 m 3种加筋间距进行对应。试验结果表明，加筋间距为0.1 m和0.15 m时模型的结构性能比较接近，而加筋间距为0.3 m时模型的结构性能有着明显的不同；这说明GRS结构和MSE结构之间有着明显的性能差异。

GRS结构和MSE结构有着各自不同的设计体系，有着不同的计算方法评价相关结构性能的量化指标。这些评价方法主要包括Wu和Adams的评价侧向位移的方法、临时指南和AASHTO规范中计算筋材轴力的方法[8,16,18]。本文在试验实测数据的基础上，对比了不同评价方法的量化指标与实测值之间的差异，以验证这些方法在GRS结构和MSE结构中的各自适用性。结果表明，不同的评价方法对GRS结构和MSE结构的适用性各不相同，这进一步说明了GRS结构和MSE结构之间存在着较大的差别，应在实际工程中引起注意。

2 试验方案

2.1 试验装置

试验模型主要按GRS桥台为原型进行设计。工程实例中，有规模较小的GRS桥台高约3 m，限于室内试验的条件，取长度相似比λ=2进行缩尺模型试验设计，以保证模型高度在试验条件允许的前提下尽可能大。对于土工结构物，填料密度的相似比一般取1，其他相似比可以根据长度相似比和填料密度相似比确定，其值如表1所示[19-21]。

GRS桥台的承载区域(即桥跨结构与GRS桥台的接触部位)通常为长条形，其长度与宽度的比值一般在7～14之间，因此可以按平面应变条件进行分析研究[11]。按平面应变条件，取试验模型的尺寸为：长度L×宽度B×高度H=2.3 m×1.0 m×1.5 m。试验装置如图1所示，模型箱由型钢及钢板构成，模型一侧临空。为保证试验模型的平面应变条件，模型箱两侧壁设置1 mm厚的聚四氟乙烯膜进行减阻，聚四氟乙烯膜与模型箱侧壁之间涂刷凡士林进行润滑[12]。

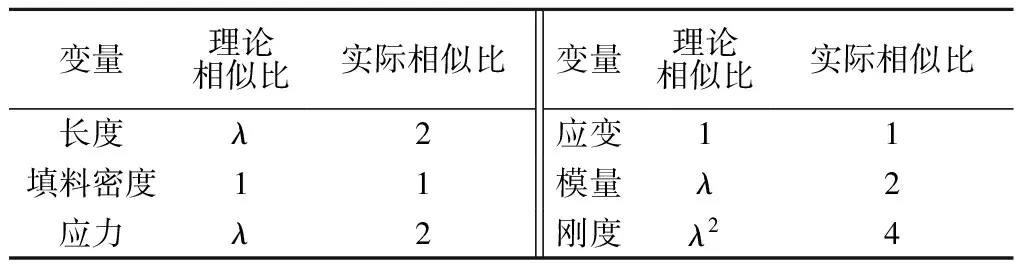
表1 模型试验的相似比Table 1 Similitude relationships for model tests

图1 模型试验装置简图Fig.1 Schematic diagram of test apparatus

试验荷载由千斤顶通过反力架施加于刚性载荷板上，载荷板宽度0.3 m，其外侧边缘距离面板内侧边缘0.1 m(即“避让距”，如图1所示)。工程中，GRS桥台的设计允许承载力一般不超过200 kPa[8]，根据应力相似比λ=2，相应的试验加压荷载应为100 kPa。本次试验即研究该级荷载条件下GRS结构与MSE结构的工作性能的差别。

2.2 试验方案

在实际工程中，GRS桥台的常用加筋间距为0.2 m或0.3 m[12]，MSE挡墙的典型加筋间距为0.6 m[17]；按长度相似比λ=2，分别取加筋间距Sv为0.1，0.15，0.3 m进行3组模型试验的对比研究，试验组号依次命名为A，B，C。即试验A和试验B的模型代表GRS结构，而试验C的模型则代表MSE结构。

2.3 填料性质

按美国临时指南[8]推荐的填料级配要求，结合本次试验选定的长度相似比λ=2，则试验用填料的级配应满足表2的要求。据此配比获得的填料为不均匀系数Cu=4.21、曲率系数Cc=0.47的均匀土，级配曲线如图2所示。填料类型为粗砂，其最大干重度γdmax和最小干重度γdmin分别为18.5 kN/m3和14.9 kN/m3。试验过程中填料分层击实，击实后的干重度γd=17.6 kN/m3，相对密度Dr=0.8。根据室内大型直剪试验，该相对密度下的填料内摩擦角φ=40°，黏聚力c= 0 kPa。

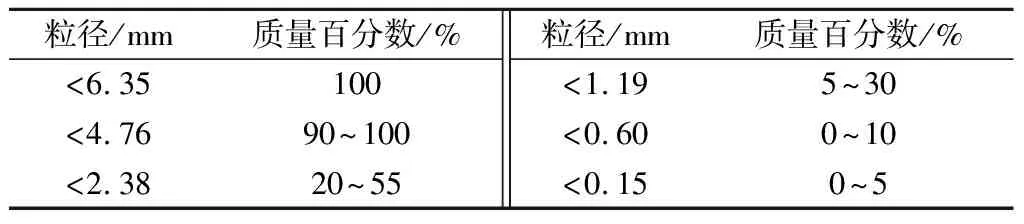
表2 试验用填料的级配要求Table 2 Gradation requirements for test fillers

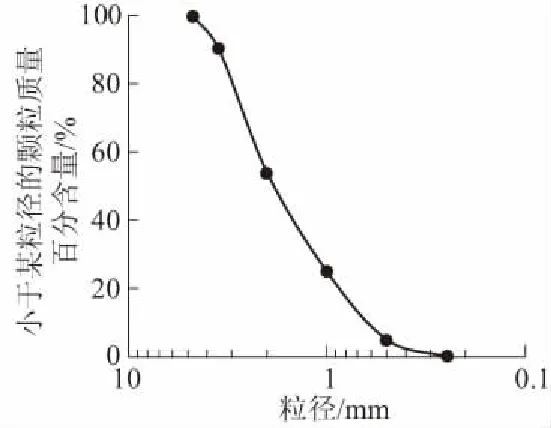
图2 试验用填料的级配曲线Fig.2 Grain size distribution of sand filler

图3 试验用土工格栅的拉伸曲线Fig.3 Tensile curve of geogrid for test

2.4 筋材性质

实际工程中，GRS桥台所用的加筋材料通常为有纺PP土工布(HPG-57型号)，极限拉伸强度70 kN/m，2%伸长率时的拉伸强度为19.3 kN/m、刚度约为965 kN/m[8]。通过宽条拉伸试验的比选，加筋材料采用TGSG25-25型聚丙烯双向土工格栅，网孔尺寸40 mm×40 mm，肋条宽度和厚度分别为3.5 mm和1.0 mm，其拉伸曲线如图3所示；其他主要力学性质参数如表3所示，能近似满足相似比要求。

表3 试验用土工格栅的参数Table 3 Properties of test geogrid

2.5 面板型式

面板材料选用如图4所示的格宾碎石笼，笼体尺寸：长度Lg×宽度Bg×高度Hg=1.0 m×0.1 m×0.1 m(或0.15 m)。笼体设置2种高度是为了不同试验组别之间加筋间距的调整。对于试验A和试验B，面层系统由格宾碎石笼垂直码放形成，筋材直接压在上、下笼体之间，即筋材与格宾碎石笼的连接方式为摩擦型连接，以此模拟实际工程中GRS结构的面层连接方式；相对应地，试验C的筋材与格宾碎石笼通过8号铅丝进行绑扎固定，以模拟MSE结构面层的机械连接型式。试验模型制作过程中，面层系统外侧通过模板进行支护，以保证面层系统的垂直度；模型制作完成后再拆除模板。

图4 格宾碎石笼面板Fig.4 Gravel gabion

图5 试验监测方案Fig.5 Test monitoring schemes

2.6 监测方案

试验过程中，对载荷板沉降、筋材应变、墙体侧向变形等进行监测，各组试验的监测元件布置如图5所示，各组试验的监测元件都布设于同一高度位置以方便对比分析。侧向百分表的安置高度自下而上分别是0.3，0.75，1.05，1.35 m；贴应变片的4层筋材的高度自下而上分别是0.3，0.6，0.9，1.2 m。靠近格宾碎石笼的第一列应变片距离笼体0.1 m，各列应变片之间相距0.4 m。

试验用应变片型号为BFH120-3AA-D100，基底尺寸6.9 mm×3.9 mm，丝栅尺寸3.0 mm×2.3 mm，电阻值120 Ω，灵敏系数2.0±1%。应变片通过502胶水粘贴在格栅节点上，粘贴前采用磨光机对格栅节点进行打磨，以增加粘贴面的平整度与粗糙度，使得应变片粘贴牢固。粘贴后的应变片表面涂抹一层703硅胶进行保护(图6)。应变片丝栅受力方向与筋材受力方向保持一致，应变数据通过YE2539高速静态应变仪采集，仪器分辨率为1 με，测量误差为±0.3% F·S。

图6 应变片粘贴形式Fig.6 Paste form of strain gauge

2.7 加载方案

实际工程中，桥跨结构的荷载通常是一次性施加在GRS桥台上的。因此，试验过程中，载荷板上的荷载一次性施加至100 kPa。

3 试验结果与分析

3.1 沉降及侧向位移分析

载荷板沉降取数显百分表读数的平均值。试验A(Sv=0.1 m)、试验B(Sv=0.15 m)和试验C(Sv=0.3 m)在100 kPa静力荷载条件下的沉降值分别为8.67，17.92，23.15 mm，相应的竖向相对变形分别为0.58%，1.19%，1.54%。试验结果表明：在密实度及其他试验条件保持一致的情况下，加筋间距越小，结构顶面的沉降越小。

图7显示了各组试验墙体的侧向位移分布规律，侧向位移基本上随着墙高的增加而增大。试验A和试验B的侧向位移相比试验C要小很多，说明加筋间距减小到一定程度时，对结构体的侧向变形能起到明显的约束作用。试验A、试验B、试验C在100 kPa静力荷载条件下的最大侧向位移分别为5.49，8.59，19.35 mm。

图7 侧向位移监测成果Fig.7 Monitored lateral displacement

如前所述，试验A和试验B的模型代表GRS结构，而试验C的模型则代表MSE结构。从上述试验结果易知：在相同的工作荷载条件下，GRS结构的顶面沉降及侧向变形比MSE结构要小很多，GRS结构表现出更好的整体刚度。

3.2 筋材应变分析

各组试验所得筋材应变的分布规律如图8所示，筋材应变随着筋材埋深的增加而减小，说明下部筋材受附加荷载的影响较小。根据现有的应变监测数据推测分析，加筋间距越小，各层筋材的最大应变越小，且应变的分布趋势更加均匀一些；这说明加筋层数的增加使筋材受力分担更均匀。

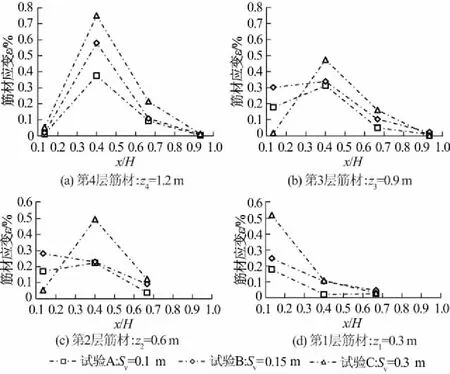
图8 筋材应变分布规律Fig.8 Distribution of strain of reinforcements

对比试验A、试验B、试验C的应变分布曲线，尤其是第1—第3层筋材的应变分布曲线，易知试验A和试验B的应变分布规律比较接近，而与试验C有着较大的差别；且在同一层筋材的水平方向上，试验A和试验B的应变分布比试验C的应变分布相对均匀。可见，GRS结构相比于MSE结构，表现出相对较好的复合体特性。

4 试验数据的理论对比分析

4.1 侧向位移的理论对比分析

Wu[22]和Adams等[8]针对GRS结构分别提出了如式(1)和式(2)所示的估算最大侧向位移的方法，估算值与试验值之间的对比如表4所示。

(1)

式中：δmax为最大侧向位移(mm)；εd为筋材最大应变；H为结构体高度(m)。

(2)

式中：DL为结构体的最大侧向位移(mm)；bq,vol为包括避让距在内的竖向荷载分布宽度(m)；Dv为结构体顶面的竖向沉降(mm)。

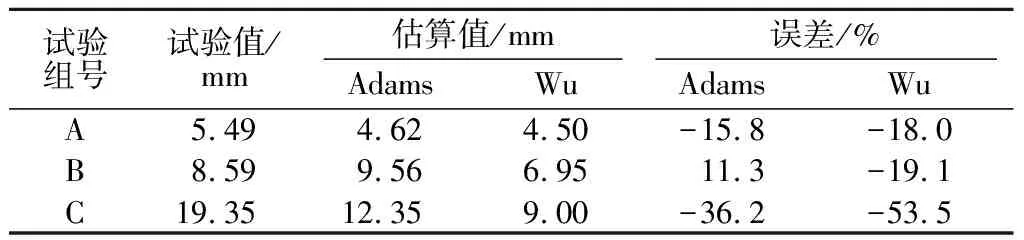
表4 最大侧向位移估算值与试验值对比Table 4 Comparison between estimated values and test values of maximum lateral displacement

对比结果表明，用Adams或Wu的方法估算GRS结构最大侧向位移的误差比估算MSE结构的要小很多，该方法对GRS结构较为适用。这从侧面说明了GRS结构与MSE结构的差异性。此外，评价GRS结构的最大侧向位移时，Adams的方法比Wu的方法较为精确。

Wu的方法是就GRS结构的相关试验数据统计分析得出的半经验公式；而Adams的方法基于GRS复合体“体积应变为0”的假设，通过实际监测的竖向沉降值进行换算得到。对于GRS结构，在“小变形”范围内，Adams的假设基本能够成立，所以其评价侧向位移的方法比Wu的方法准确。

4.2 筋材轴力的理论对比分析

对于GRS结构，美国临时指南[8]给出了如式(3)—式(4)所示的计算每层筋材最大轴力的半经验公式；对于MSE结构，AASHTO规范[18]给出了如式(5)—式(6)所示的计算公式；而每层筋材的最大应变与筋材刚度的乘积可以认为是其最大轴力的试验值。三者的对比如图9所示。

(3)

σh=σh,W+Δσh,q。

(4)

式中：Tr为筋材轴力(kN/m)；σh为任意深度处土体的水平向总应力(kPa)；σh,W为任意深度处土体自重引起的水平向应力(kPa)；Δσh,q为任意深度处由超载引起的水平向应力(kPa)，采用Boussinesq方法估算；dmax为填料的最大颗粒直径(m)。

Tmax=σH maxSv；

(5)

σH max=γp(σvkr+Δσvkr+ΔσH) 。

(6)

式中：Tmax为筋材最大轴力(kN/m)；σH max为任意深度处土体的水平向总应力(kPa)；σv为任意深度处土体的竖向自重应力(kPa)；Δσv为任意深度处由超载引起的竖向附加应力(kPa)，采用AASHTO规范方法估算；kr为侧向土压力系数，这里取kr=ka，ka为主动土压力系数；ΔσH为其他水平向附加应力(kPa)，这里为0；γp为荷载调整系数，取1.5。