初始孔隙比对高吸力下非饱和土土水特性的影响
2022-07-15陈嘉伟熊勇林丁瑞旋
陈嘉伟 ,李 泽 ,韩 哲 ,高 游 ,熊勇林 ,丁瑞旋
(宁波大学土木与环境工程学院, 浙江 宁波 315211)
土水特性影响着很多岩土体的基本特性,如土石坝渗流、坡体强度、地基变形等,常用吸力与含水率或饱和度的关系曲线来表示[1]。影响土水特性的因素有很多,包括土的矿物成分[2-3]、应力历史[4-5]、初始孔隙比[6]等。土的矿物成分对土水特性的影响较大,Lu等[2]指出随着黏性矿物含量的增大,其滞回特性会更明显。对于同一类型的土,在相同的温度下,应力历史和初始孔隙比是影响土水特性的主要因素[4-7]。伊盼盼等[8]通过压力板试验量测了非饱和重塑粉土的土水特性,并分析了初始干密度和含水率对土水特性的影响;蔡国庆等[9]在分析典型土水特征曲线模型的基础上提出了一种考虑初始孔隙比影响的土水特征曲线预测方法;张佳伟等[10]采用滤纸法测量并分析了不同初始干密度对南阳膨胀土土水特性和抗剪强度的影响;于沉香等[11]利用颗分曲线实现了对不同初始孔隙比土水特征曲线的预测。Sun等[12]和邹维列等[13]通过一系列土水特征曲线试验研究了应力状态和初始孔隙比对土水特征曲线的影响,并认为应力状态对试样持水特性的影响主要通过改变土体的孔隙比产生。在相同温度环境下,同类型土孔隙比才是影响土水特征曲线的主要因素[14]。上述针对初始孔隙比对土水特性影响的研究中,实测数据大多通过压力板仪,利用轴平移技术控制土样的吸力,然而由于压力板仪中配置的陶土板最大进气值为1.5 MPa,这种方法只能测量低吸力范围内(即吸力值<1.5 MPa)的土水特征曲线。因此,目前对高吸力下考虑孔隙比影响的土水特性曲线试验研究和模拟还比较欠缺。
本文以粉土为试验材料,通过饱和盐溶液蒸汽平衡法对压实粉土试样进行高吸力下的土水特性试验,吸力范围为3.29~286.7 MPa。首先分析了初始孔隙比对高吸力下土水特性的影响;其次,基于试验结果,提出了全吸力范围内考虑初始孔隙比影响的土水特征曲线方程,并将其应用于非饱和相对渗透系数的预测中,结合实测值进行对比和分析,验证了所提出土水特征曲线方程的可靠性。
1 试验材料及试验方法
1.1 试验材料
试验所用的土样为粉土,其基本物理指标如表1所示。土样的黏粒和粉粒分别约占10%和90%。

表1 试验粉土基本物理指标Table 1 Physical indices of silt
试验所用的土样均为压实土样,制备过程为:将土样风干碾碎,过2 mm标准筛并烘干,再配制目标含水率的土样;将配制好的土样放入保鲜袋中密封24 h后,利用环刀模具制成直径61.8 mm、高20.0 mm的试样。控制试样的初始含水率约为15.2%,初始孔隙比(e0)为0.93,0.69,0.50。初始孔隙比的控制方法为:根据已知含水率、目标孔隙比和压实土样体积计算得到所需土样的质量,再将一定质量的土样装入特制的固定体积环刀压样模具(图1)中进行压制,即可得到目标孔隙比的试样。

图1 制样模具及试样Fig.1 Specimen preparation mould
1.2 试验原理与方法
1.2.1 试验原理
通过不同的饱和盐溶液控制密闭保湿缸内的相对湿度(图2),从而达到控制土试样吸力的目的。吸力与孔隙水相对湿度间的热动力学关系为[1]:

图2 蒸汽平衡法的密闭容器Fig.2 Sealed container for the vapor equilibrium technique
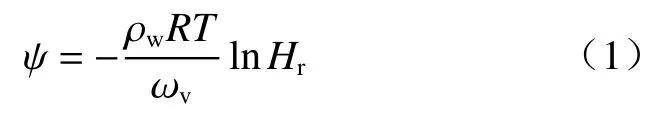
式中:ψ——总吸力/MPa;
ωv——水蒸气的分子量,取18.016 g/mol;
R——理想气体常数,取8.314 J/(mol·K);
T——绝对温度/K;
Hr——相对湿度/%;
ρw——水的密度/(g·cm-3)。
1.2.2 试验方法
将制备好的试样切块后放入不同的饱和盐溶液缸中密封平衡(图2),每个密封缸中相同初始状态的土样放2块,1块用于量测含水率(w),1块用于量测体积。达到平衡之后,打开密封缸迅速测量1块不规则土样的含水率,采用阿基米德原理对另1块不规则土样的体积大小进行量测[15],量测装置如图3所示。最后,再计算特定饱和盐溶液平衡后土样的孔隙比、饱和度等参数,即可计算得到高吸力下不同初始状态土样的土水特性数据。此试验选取的饱和盐溶液及其对应的吸力值如表2所示[16]。

表2 饱和盐溶液及对应吸力值(20 °C)Table 2 Saturated salt solution and corresponding suction
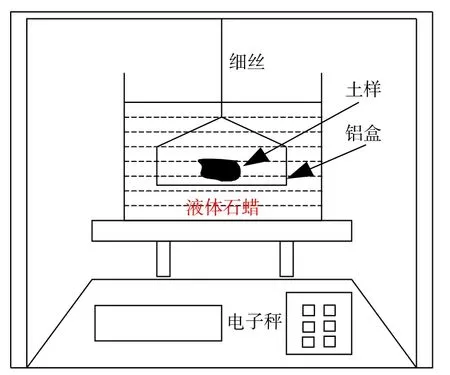
图3 土样体积测量装置Fig.3 Sketch of volume measurement for soil sample
2 结果与分析
2.1 高吸力下孔隙比对土水特性的影响
图4为饱和盐溶液蒸汽平衡法控制的高吸力下(3.29~286.7 MPa)不同初始孔隙比(e0=0.93,0.69,0.50)非饱和土试样的土水特征曲线。由图4(a)含水率与吸力的关系曲线可知,不同初始孔隙比的土水曲线几乎重合,也就说明初始孔隙比对以含水率与吸力关系表示的土水曲线几乎没有影响,文献[13]也得到了相似的结论。高吸力下土水特性主要与吸附水的含量相关[17],且与土颗粒的比表面积等相关,而对于同种土样,单位质量的土颗粒比表面积相同,因此土水曲线表示为含水率与吸力的关系时,初始孔隙比对高吸力段的土水曲线几乎不存在影响。故高吸力段的吸力可根据含水率与吸力关系曲线确定。
由图4(b)饱和度与吸力关系曲线可知,初始孔隙比小的试样,土水特征曲线向右上方略微移动,说明以饱和度(Sr)表示的土水特征曲线会受初始孔隙比的影响。由Sr=Gsw/e0(Gs为土颗粒比重)的关系可知,对于同一种土体,当含水率相同时,饱和度即为孔隙比的单值函数且与其呈反比关系,初始孔隙比变小或干密度变大,土水特征曲线就会向右上方略微移动。因此,研究高吸力下孔隙比对土水特征曲线的影响可为提出适用于高吸力下考虑孔隙比影响的土水模型奠定基础。

图4 高吸力下不同初始孔隙比土样的土水特征曲线Fig.4 Soil-water characteristics curves of soil sample with different initial void ratios at high suctions
2.2 高吸力下典型土水方程的适用性分析
高吸力下的非饱和土在自然界中普遍存在,尤其是在半干旱或干旱地区。如我国的西北地区,土体长期处于相对湿度很低的环境下,土体的吸力(s)可能会达到几十或者几百兆帕。因此,高吸力下非饱和土的土水特征试验及其预测方法的研究都具有重要的现实意义。
目前,若要获取广吸力范围的土水特征曲线,往往要结合不同的量测方法且耗时非常长。很多学者都提出了土水特征曲线的拟合方程,如表3所示。表3中的土水曲线拟合方程的验证数据大多采用低吸力下的实测值来验证,其实测值主要通过压力板仪测得,仪器的吸力量测范围为0~1.5 MPa。因此,有必要对几种典型土水特性曲线方程在高吸力范围内的适用性进行讨论和分析。

表3 典型的土水特征曲线方程Table 3 Typical soil water characteristic curve equations
由表3可知,Brooks-Corey模型可模拟过渡区线性段的土水特性,无法对边界区和残余区的土水特征曲线进行准确地模拟。Van-Genuchten模型和Gardner模型在边界区和过渡区的模拟结果较好,但在最大吸力值106kPa时,模型曲线不能通过零点,在残余区即高吸力范围的模拟结果较差。Fredlund-Xing模型和Romero-Vaunat模型在全吸力范围内均能较好地模拟土体的土水特征曲线,主要原因是这2个模型中均存在高吸力范围的修正项C(s)。因此,高吸力修正项对高吸力范围内土水特征曲线的模拟非常关键。
2.3 高吸力下考虑孔隙比影响的土水曲线方程
对高吸力下土水特征曲线的准确拟合是预测非饱和土强度及其本构关系的基础。目前,已有学者提出了考虑初始孔隙影响的土水特征曲线方程,如Gallipoli等[23]提出考虑初始孔隙比影响的土水曲线方程,该方程主要基于VG模型[19]引入初始孔隙比的指数关系项来考虑初始孔隙比的影响,其土水特征曲线方程为:
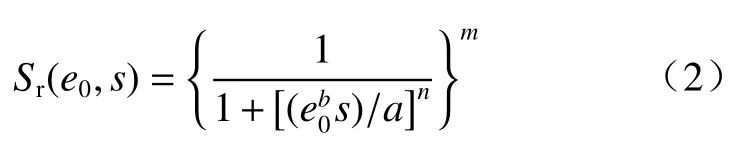
式中:a、b、m、n——拟合参数。
由式(2)可知,Gallipoli的方程是基于VG模型提出的,其在高吸力下无法准确地模拟土水特性。在非饱和土强度预测公式中,非饱和强度增强项通常与土水特征曲线中的饱和度有关;高吸力下土样的吸力值很高,若不能准确拟合饱和度,高吸力下的非饱和增强项计算就会存在很大的误差。
为了准确模拟不同类型土在全吸力范围内的土水特征曲线,将Fredlund等[20]提出的高吸力修正项引入式(2),高吸力修正项的表达式为:

式中:ψre——残余吸力值/kPa。
Fredlund等[20]通过对大量实测数据的拟合与分析,指出ψre的取值在1 500~3 000 kPa范围内可获取较好的拟合结果。因此,为了简便,本文统一取ψre=1 500 kPa。
将式(3)引入式(2),即得到全吸力范围内考虑初始孔隙比影响的土水特征曲线方程:

分别利用式(2)和(4)拟合本文试验所测高吸力下不同初始孔隙比粉土试样的土水特征曲线(图5),式(2)(4)中的4个拟合参数a、b、m、n分别为83.9,0.72,0.72, 2和0.923,2.42,0.095,4.5。
由图5可知,高吸力下原始的式(2)拟合效果差,且不能满足最大吸力值106kPa时饱和度为0的状态。而修正后的式(4)能较好模拟全吸力范围内不同初始孔隙比的土水特性,尤其是高吸力范围的土水特性,即在吸力最大值条件下,不同初始孔隙比的土水特征曲线均通过零点。

图5 修正后的方程拟合土水特征曲线结果Fig.5 Fitting of SWCCs by the proposed equation
图6为利用式(4)拟合的不同初始孔隙比下不同类型土的土水特征曲线,包括南阳膨胀土[10]、粉质黏土[4]和砂质粉土[24]。表4为3种类型土各粒组的质量分数。
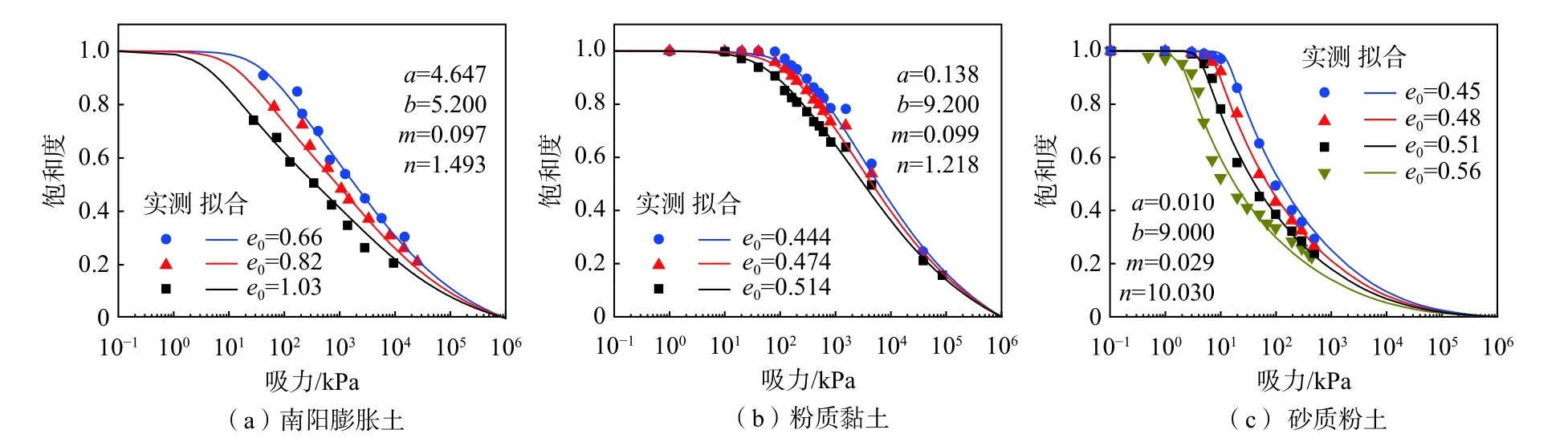
图6 修正后的方程拟合土水特征曲线结果Fig.6 Fitting of soil water characteristic curves by proposed equation

表4 不同类型土的粒组成分Table 4 Particle size composition of different soils
由图6可知,式(4)能较好模拟不同类型土全吸力范围内不同初始孔隙比的土水特征曲线,尤其是高吸力范围的土水特性,即在吸力最大值条件下,不同初始孔隙比的土水特征曲线均过零点。因此,本文提出的土水特征曲线方程能较好地模拟不同类型的非饱和土在全吸力范围内不同初始孔隙比的土水特性。
3 考虑孔隙比影响的非饱和渗透预测
一般情况下,直接测量非饱和土的渗透系数比较困难,因此常采用间接方法估算或预测非饱和土的渗透系数。近几十年,很多学者基于土水特征曲线提出了非饱和土相对渗透系数的预测方法,如Fredlund等[25]和Burdine等[26]提出的渗透系数预测模型。但考虑初始孔隙比影响的非饱和渗透系数研究还比较少。因此,将上述考虑初始孔隙比影响的土水特征曲线方程应用到非饱和相对渗透系数预测中,提出考虑初始孔隙比影响的相对渗透系数计算方法。
3.1 理论基础
目前应用较多的非饱和土相对渗透系数预测模型是Fredlund等[25]基于统计模型进行修改得到的,其积分形式为:
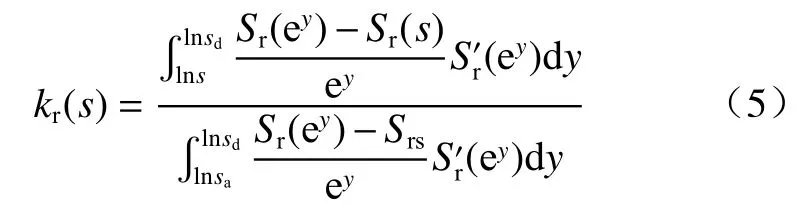
式中:e——自然底数;
sd——最大吸力值,取106kPa;
sa——进气值/kPa;
Srs——试样饱和时的饱和度。
基于上述模型,引入式(4)可得到在不同初始孔隙比下的相对渗透系数预测方程,表达式为:
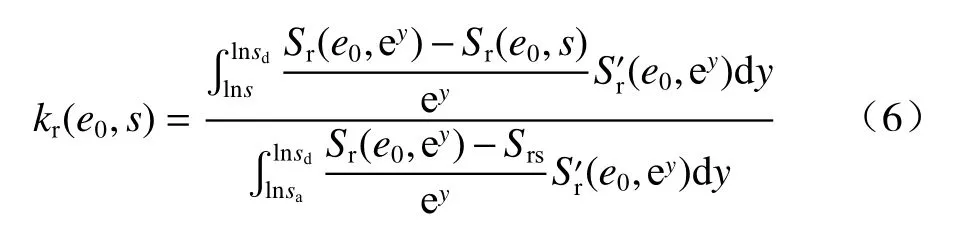
为式(4)的导数,相应表达式为:
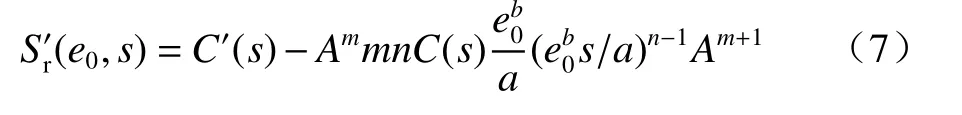
C′(s)为式(3)的导数,其表达式为:
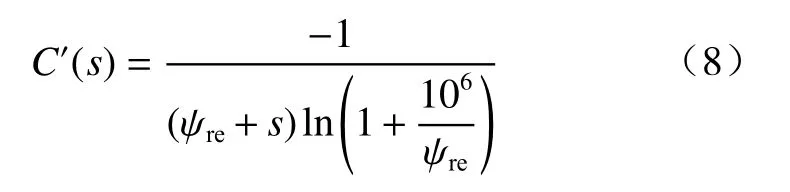
因此,只要式(4)中的4个拟合参数确定,即可用其模拟任意初始孔隙比下土的土水特性,再结合式(6)(7)(8)对非饱和土不同初始孔隙比的非饱和相对渗透系数进行预测。
3.2 试验验证
图7为不同初始孔隙比下粉砂壤土的土水特征曲线的模拟结果。实测值取自文献[27],试样的初始孔隙比分别为0.972,0.862,0.754。利用任意2组实测土水特征曲线进行拟合,确定式(4)中土水特征曲线参数a、b、m、n的取值分别为4.96,0.9,0.06,23.69。本文采用0.972和0.862的2个孔隙比的土水曲线进行标定,待参数确定后即可预测任意孔隙比下的土水曲线,图7(c)即为孔隙比为0.754时土水特征曲线的预测结果。由图可知,修正后的土水特征曲线方程式(4)能较好地模拟广吸力范围内不同初始孔隙比的土水特征曲线。
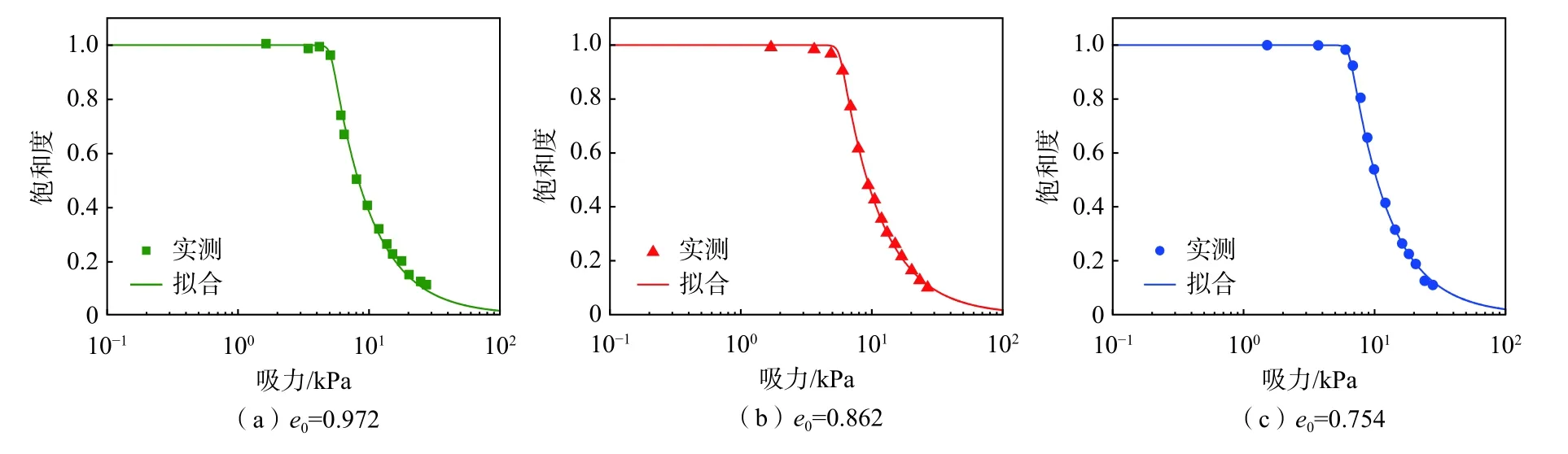
图7 不同初始孔隙比粉砂壤土土水特性的模拟结果Fig.7 Fitting of soil water characteristic curves of silty sand with different initial void ratios
图8为Touchet粉砂壤土在初始孔隙比分别为0.653,0.733,0.815时的相对渗透系数的预测结果。由图可知,式(6)对于Touchet粉砂壤土相对渗透系数的预测结果与试验数据较为吻合,说明本文提出的方法能够较好地预测广吸力范围内不同初始孔隙比的非饱和相对渗透系数。

图8 不同初始孔隙比的粉砂壤土相对渗透系数预测Fig.8 Prediction of relative permeability coefficient of silty sand with different initial void ratios
4 结论
(1)通过饱和盐溶液试验结果可知,土水特征曲线表示为含水率与吸力的关系时,初始孔隙比对高吸力段的土水特征曲线几乎不存在影响。故高吸力段的吸力可根据含水率与吸力的关系曲线确定。
(2)将Fredlund-Xing模型中的高吸力修正项引入现有考虑孔隙比影响的Van-Genuchten土水特征曲线方程,获得了一个全吸力范围内考虑孔隙比影响的土水特性曲线方程,结合不同初始孔隙比条件下三种类型土的实测数据对该方程进行了验证。
(3)基于考虑孔隙比影响的土水特征曲线方程,提出了考虑孔隙比影响的非饱和土相对渗透系数的修正预测方程,利用不同初始孔隙比条件下粉砂壤土的土水曲线与相对渗透系数的试验数据验证了该方程的可行性。
