基于贝叶斯方法优效非劣效性试验转换研究*
2019-03-19中国药科大学生物统计与计算药学研究中心210009蒋丽芸尹竹琳言方荣
中国药科大学生物统计与计算药学研究中心(210009) 于 莉 蒋丽芸 尹竹琳 言方荣
【提 要】 目的 基于Bayesian框架,讨论由优效性向非劣效性试验转换,或由非劣效性向优效性试验转换时,试验的Ⅰ类错误率能否控制在可接受范围内。方法 通过不同场景下模拟得到的全局Ⅰ类错误率予以验证,并对设计中的重要参数进行敏感性分析。结果 模拟结果表明,在一般条件下,全局Ⅰ类错误率都能很好的控制在0.1以内,而在稍加严格的条件下,全局Ⅰ类错误率可控制在0.05以内。结论 由优效性向非劣效性试验转换,或由非劣效性向优效性试验转换时,整个试验的Ⅰ类错误率能得到有效的控制。
Ⅱ期临床试验主要用来检验新药的有效性,应用安慰剂或已上市药物作为对照药对新药的疗效进行评估,而进行随机临床试验(randomized clinical trial,RCT)是比较不同药物疗效的最佳方法。根据不同的试验目的,可以将RCT分为优效性试验、非劣效性试验及等效性试验。优效性试验旨在验证新药的疗效是否优于标准药物或安慰剂;非劣效性试验旨在验证新药的疗效是否不比标准药物差;等效性试验旨在验证新药的疗效是否与标准药物的疗效相当[1-2]。传统的RCT设计中,根据不同的目的选择相应的试验类型,受试者完全入组后对所得的受试者数据进行检验,一旦检验结果不能达到预期目标,则试验失败,前期的投入也将付之东流。为了尽可能减少企业的损失、提高新药申报的成功率,一个解决方法是:如果原先进行的是优效性试验,则可以选择下调试验目标,再进行一次非劣效性检验,若二次检验得出该新药满足非劣效性,则试验成功,可以继续进入Ⅲ期临床试验[3]。而对于检验结果已达到预期且有望达到更高目标时,同样可以上调试验目标,对应的过程即由非劣效性试验“升级”为优效性试验。
欧盟药品局(European Medicines Agency,EMA)曾出台指导原则[4]专门探讨了这种上调或下调试验目标的方法:即当优效性检验的结果不显著时,若能接受非劣效性的结果且存在预设的非劣效边界,则可以下调试验目标,进行非劣效性检验;当非劣效性检验的结果有可能超出预期达到优效性时,则可以进行一次优效性检验加以验证。然而,一个核心的问题是如何在进行两次检验时控制Ⅰ类错误。通常,对于单个的假设检验,需要将Ⅰ类错误率控制在0.1或0.05以内;而上述优效性试验转换为非劣效性试验或非劣效性试验转换为优效性试验的过程中,由于改变了试验目的,需要进行两次假设检验,若每次检验的Ⅰ类错误率都控制在0.05以内,那么进行两次检验自然就遇到全局Ⅰ类错误率是否会膨胀的问题,然而,EMA的指导原则中并未做出详细说明。综上,本文基于贝叶斯框架对优效非劣效试验相互转换问题进行了研究,并通过多种场景下的模拟,探讨了在这种转换试验目标的情况下其Ⅰ类错误率的控制问题。
原理及方法
1.优效性试验及非劣效性试验的假设检验原理
优效性试验是为了证明新药的疗效优于已存在的药或安慰剂,其原假设(H01)为新药的反应率(pT)不高于标准药的反应率(pC),备择假设(H11)为新药的反应率(pT)高于标准药的反应率(pC),即
H01:pT≤pCH11:pT>pC+δ
其中δ为优效边界。
非劣效性试验[5]是为了证明新药的疗效不比已存在的药差,其原假设(H02)为新药的反应率(pT)低于标准药的反应率(pC)且超出了临床可接受范围,备择假设(H12)则为新药的反应率(pT)不比标准药的反应率(pC)差,即
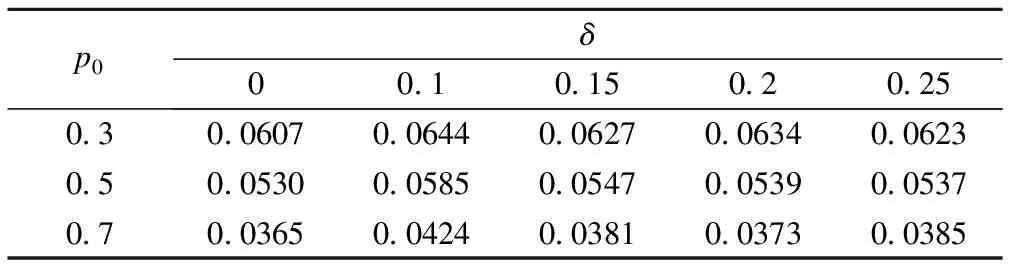
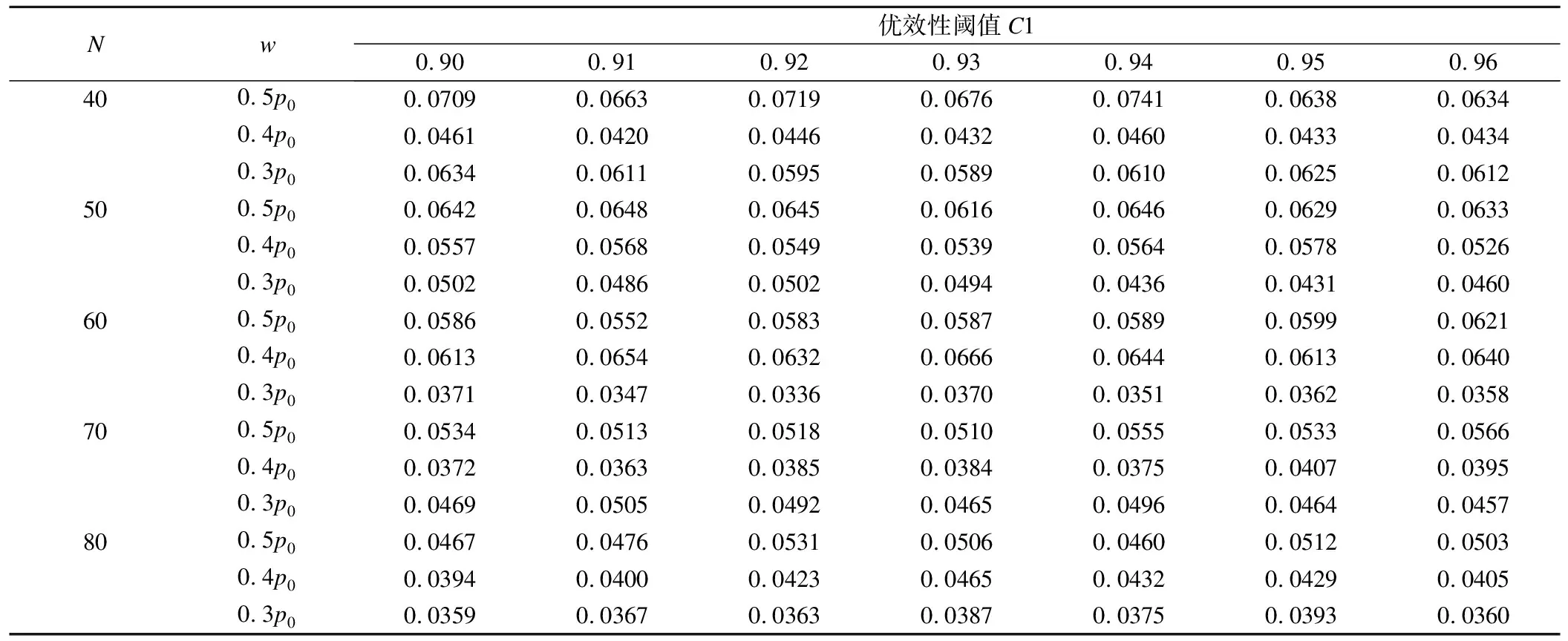
H02:pT 其中w为非劣效边界[6-7]。 本文采用双臂试验,且选用阳性对照。假定实验组和对照组分别入组N个受试者,各组有疗效反应的人数分别为y1,y2,假定新药和标准对照药的有效反应率服从先验分布beta(a,b),由共轭性可知,后验分布分别为pT|Dn~beta(a+y1,b+m-y1),pC|Dn~beta(a+y2,b+m-y2)。 2.优效性试验转为非劣效性试验 优效性转非劣效性试验流程如图1a所示: (1)首先进行优效性检验。入组预定数目的受试者,根据所得的受试者数据判断新药比标准药物有效的后验概率值Pr(pT>pC+δ|Dn)是否满足Pr(pT>pC+δ|Dn)≥C1(C1为优效性阈值,一般在(0.9,1)内取值),若满足,则拒绝H01,认为新药的疗效优于标准药;否则,接受H01,说明新药的疗效不理想,则进一步接受条件更为宽松的检验,即非劣效性检验。 (2)进行非劣效性检验。根据已获得的受试者信息判断新药不比标准药差的后验概率值Pr(pT≥pC-w|Dn)是否满足Pr(pT≥pC-w|Dn)≥C2(C2为非劣效性阈值,一般在(0.9,1)内取值),若满足,则拒绝H02,认为新药的疗效不劣于标准对照药;否则,接受H02,认为新药比标准药差,且超出了临床可接受范围。 图1 流程图,a为优效性转非劣效性试验流程,b为非劣效性转优效性试验流程 3.非劣效性试验转为优效性试验 非劣效性转优效性试验流程与上述相反,如图1b所示: (1)首先进行非劣效性检验。入组预定数目的受试者,根据所得的受试者数据判断新药疗效不比标准药差的后验概率值Pr(pT≥pC-w|Dn)是否满足Pr(pT≥pC-w|Dn)≥C2(C2为非劣效性阈值,一般在(0.9,1)内取值),若不满足,则接受H02,认为新药与标准药相比疗效太差,不能接受;否则,拒绝H02,说明新药疗效可观,则接受进一步的条件更为严格的检验,即优效性检验。 (2)进行优效性检验。根据已获得的受试者信息判断新药比标准药物有效的后验概率值Pr(pT>pC+δ|Dn)是否满足Pr(pT≥pC-w|Dn)≥C1(C1为优效性阈值,一般在(0.9,1)内取值),若满足,则拒绝H01,认为新药的疗效与标准药相比更优;否则,接受H01,认为新药的疗效并不优于标准药,但也不过差于标准药,即为非劣效的。 4.全局Ⅰ类错误 第Ⅰ类错误,也称为“弃真”错误,是指在统计检验时,在原假设H0为真的情况下,作出了拒绝原假设,即“弃真”的一种错误推断,Ⅰ类错误可记为Pr(H1|H0)。在本文中,以上述非劣效性试验转为优效性试验为例,其步骤为先进行非劣效性检验,若拒绝原假设H02则进行优效性检验,当试验最终得到非劣效结果(接受H01)为“真”时,却做出优效或劣效的推断(拒绝H01),则犯了Ⅰ类错误。由于优效性检验是在H02不成立的条件下进行的,所以该Ⅰ类错误(拒绝H01)其实是综合考虑了本设计中的两个假设检验,故称为全局Ⅰ类错误。 根据封闭检验原理[8],即当需要检验多个假设且整体Ⅰ类错误率为α时,如果在局部水平α上拒绝了涉及H0i的所有可能的交叉假设,则可以在α水平上拒绝H0i。同样地,对于上例中存在两个假设检验的情况,若在α水平上拒绝了H01∩H02,则可以在α水平上拒绝H01。由对两个检验的原假设的定义可知H01∩H02=H02,因此,换句话说,在非劣效性试验转为优效性试验的情况下,若非劣效性检验的Ⅰ类错误率(拒绝H02)能控制在α水平上,则全局Ⅰ类错误率理论上可以控制在α水平上。同理,在优效性试验转为非劣效性试验的情况下,若在α水平上拒绝了H01∩H02,则可以在α水平上拒绝H02,由于H01∩H02=H02,所以同上,全局Ⅰ类错误率仍然可控制在水平α上。 综上可知,当优效非劣效性试验相互转换时,其全局Ⅰ类错误率能够得到有效的控制,且由非劣效性检验的Ⅰ类错误率决定。 1.模拟试验设置及结果 设计中涉及到的参数:(p0,δ,w,C1,C2,N),p0为标准药的初始有效反应率,δ为优效边界,w为非劣效边界,C1为优效性阈值,C2为非劣效性阈值,N为最大样本量。假定一组取值:p0=(0.3,0.5,0.7),δ=(0,0.1,0.15,0.2,0.25),w=0.5*p0,C1=C2=0.95,N=50,并采用无信息先验beta(0.6,1.4)作为pT、pC的先验分布进行模拟。 表1、2分别为优效性试验转为非劣效性试验以及非劣效性试验转为优效性试验的10000次模拟结果,从数据可以直观地看出,在p0与δ的不同取值下Ⅰ类错误率都能控制在0.1以内。 通过以上模拟,进一步验证了存在多个假设检验的情况下,全局Ⅰ类错误率能够控制在合理的范围内,即不会出现全局Ⅰ类错误率膨胀的情况。 表1 优效性试验转为非劣效性试验的10000次模拟结果 表2 非劣效性试验转为优效性试验的10000次模拟结果 2.敏感性分析 由表1、2可以看出,标准药的初始有效反应率p0对试验的Ⅰ类错误率有较大影响,且随着p0的增大呈下降趋势;而优效边界δ的变化对试验的Ⅰ类错误率几乎无影响。 进一步考虑样本量N、非劣效边界w及阈值C1、C2的变动对全局Ⅰ类错误率的影响。其余变量值固定为:p0=0.3,δ=0.1。以优效性试验转为非劣效性试验为例,模拟结果见表3、4(非劣效性试验转为优效性试验结果类似),其中第一行为阈值的几种取值情况,第一列表示样本量,对于每个样本量值,有3种非劣效边界的取值。 由表3、4可以看出,全局Ⅰ类错误率基本可以控制在0.1以内。不同样本量N之间的全局Ⅰ类错误率有所差异,但总体来看差异并不明显;不同的非劣效边界w对试验的Ⅰ类错误率有一定的影响;优效性阈值C1的变动对全局Ⅰ类错误率几乎无影响,而对于不同的非劣效性阈值C2,试验的Ⅰ类错误率波动很大。当C2=0.9时,Ⅰ类错误率较大在0.1左右,当C2=0.96时,Ⅰ类错误率均小于0.05,总的来说,试验的Ⅰ类错误率随着C2的增加呈下降趋势。 表3 优效转非劣效试验中样本量N、非劣效边界w及优效性阈值的变动对全局Ⅰ类错误率的影响 *:此时C2固定为0.95。 表4 优效转非劣效试验中样本量N、非劣效边界w及非劣效性阈值的变动对全局Ⅰ类错误率的影响 *:此时C1固定为0.95。 模拟研究结果表明,无论是优效性试验转换为非劣效性试验还是非劣效性试验转换为优效性试验,一般条件下,其Ⅰ类错误率都能控制在0.1以内,而在稍加严格的条件下,如增大非劣效性阈值,则全局Ⅰ类错误率可控制在0.05以内。 通过敏感性分析可知,非劣效性阈值对试验的Ⅰ类错误率的影响很大,甚至会影响到定性判断,这是因为非劣效性阈值的大小直接影响到了非劣效性检验的Ⅰ类错误率从而导致全局Ⅰ类错误率的较大变化。由以上数据可直观地看出,当非劣效性阈值的取值大于0.91时是比较安全的,即能确保Ⅰ类错误率小于0.1。推荐非劣效性阈值取为0.95,此时的Ⅰ类错误率几乎在0.05左右;若考虑进一步削减试验的Ⅰ类错误率,则可以选择稍大一点的非劣效性阈值,如0.96,此时的全局Ⅰ类错误率均控制在0.05以内。而不同的标准药初始有效反应率p0对试验的Ⅰ类错误率也有较大影响,p0越大,试验的Ⅰ类错误率则越小。p0的取值一般根据标准药的历史试验给出。 对于其他参数的取值,其中优效性阈值一般取为0.95,由于该阈值对全局Ⅰ类错误率的影响甚微,因此也可以在其附近取值。而非劣效边界值一般情况下可以取0.5*p0(p0为标准对照药的初始有效反应率),但最优的非劣效边界值并非是固定的,需视不同药物的情况而定。 本文基于贝叶斯框架就优效性试验与非劣效性试验转换时Ⅰ类错误率的控制问题进行了模拟研究分析,验证了其全局Ⅰ类错误率能得到有效的控制,证明了优效性试验与非劣效性试验相互转换的可行性,在实际临床中可加以应用。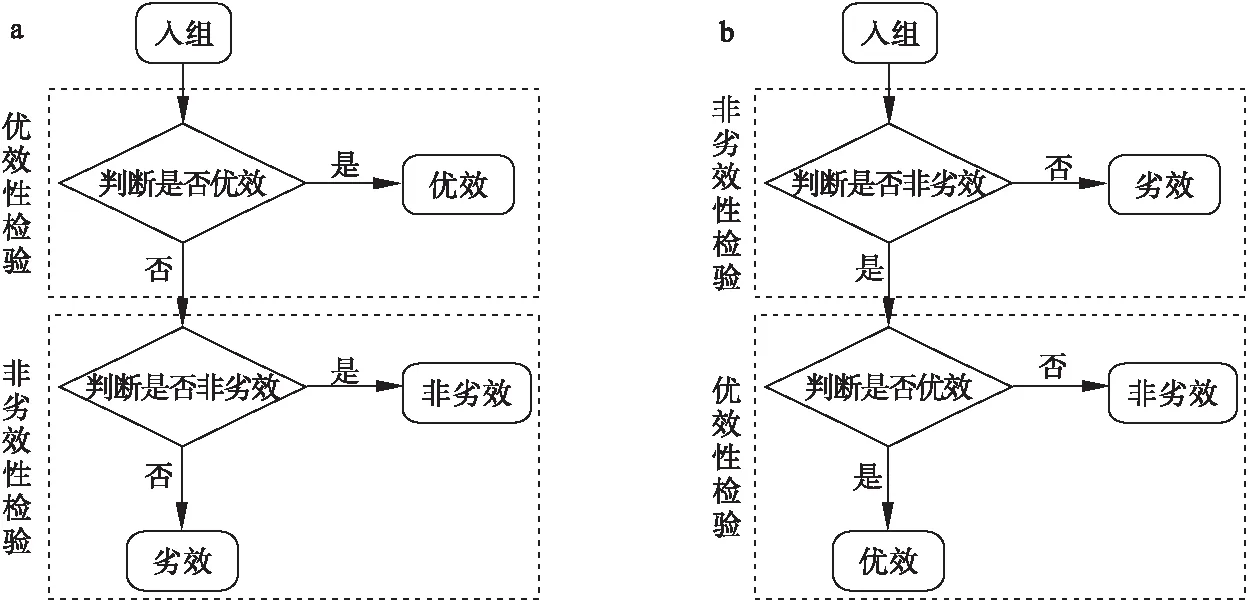
模 拟


讨 论
