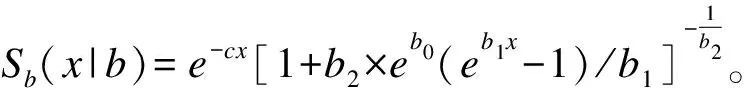R软件BaSTA包在恶性肿瘤患者生存分析中的应用*

华东理工大学理学院(200237) 干晨晨 钱夕元

国内对恶性肿瘤患者的生存分析研究大部分是以医院数据为基础的临床生存分析。为了获得恶性肿瘤患者出院后的生存情况，传统的方式是对病人进行随访。由于随访工作普遍存在花费大，时间久，效率低等缺点，寻求更加简便高效的方法成为了一个亟待解决的难题。Fernando Colchero[1]等人开发了一种专门用于生存分析的R软件包BaSTA(Bayesian survival trajectory analysis)，即贝叶斯生存轨迹分析。该包采用捕获-再捕获方法，利用贝叶斯框架，对种群的年龄别死亡率和生存率进行估计。本文尝试着将BaSTA包在恶性肿瘤患者这一特殊种群中进行应用，借助已有的住院病人医疗记录、档案等对患者的年龄别死亡率和生存率进行估计。

生存模型及BaSTA包简介

1.生存模型简介

在研究种群年龄别死亡率和生存率的捕获-再捕获实验中，每个个体i(i=1,2,…,n)均涉及到两组数据。第一组是描述该个体纵向捕获历史的二进制变量，即yi={yi,t}。若yi,t=1，则表示个体i在时间t被捕获到了；若yi,t=0，则表示没有被捕获到。

第二组数据描述了该个体的出生时间(bi)与死亡时间(di)。其中，部分个体的出生时间或者死亡时间是缺失的，这可能是它在实验之前出生(左侧截断)或者在实验结束之后才死亡(右侧删失)，也可能是它在实验期间发生了死亡但未被捕获到。

通常，对于捕获-再捕获数据集的年龄别生存分析，主要是通过结合生存模型和捕获概率模型来进行的。分别用x表示年龄，X表示死亡年龄，θ表示生存参数。假设年龄x连续，则年龄别死亡率为

(1)

因此，生存到年龄x的概率，即生存函数为

(2)

那么相对应的在年龄x之前发生死亡的概率为

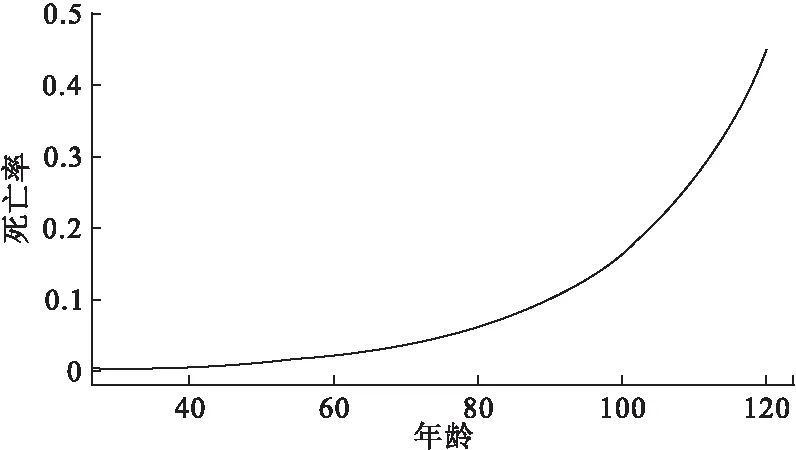
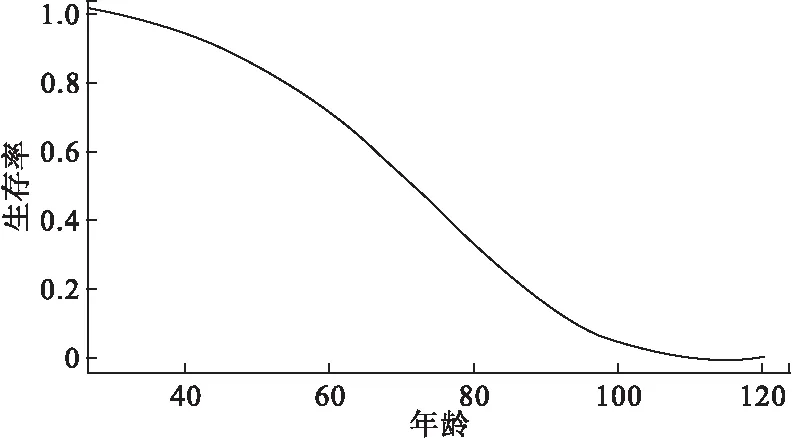
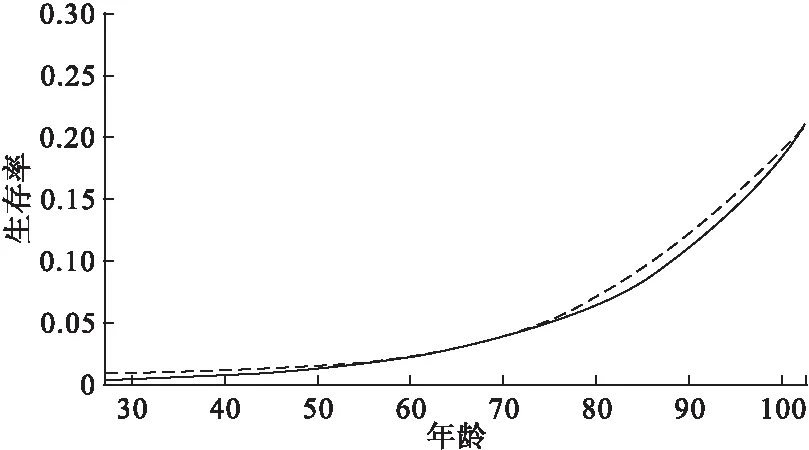
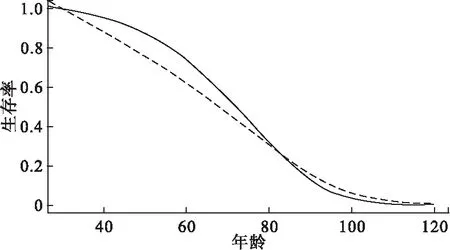
F(x|θ)=Pr(X

(3)

且死亡年龄的概率密度函数为

f(x|θ)=Pr(x≤X<(x+Δx))=S(x|θ)μ(x|θ)

(4)

在这里，我们采用贝叶斯方法分别对生存参数θ，未知死亡年龄Xu以及捕获概率π进行估计。

首先，生存参数的条件后验分布为

p(θ|Xu,Xk)∝p(Xu,Xk|θ)p(θ|θp)∝f(X|θ)p(θ|θp)

其中，p(θ|θp)是生存参数θ的先验分布。

其次，若个体i在第一次捕获之前和最后一次捕获之后共有ηi年未被捕获到，则未知死亡年龄Xu的条件后验分布为

p(Xu|Xk,θ,yu,π)∝p(yu|π,Xu)p(Xk|Xu,θ)p(X|θp)∝(1-π)ηf(X|θ)p(X|θp)

最后，由于捕获概率π的似然函数为二项分布密度的乘积，同时取其先验为具有超参数ρ1和ρ2的Beta先验，则捕获概率π的共轭Beta条件后验为

在该贝叶斯分层框架下，只需利用Metropolis-within-Gibbs[2]采样方法就可以获得上述三者的估计值。

2.BaSTA包简介

BaSTA包采用贝叶斯方法，对一个部分数据缺失的捕获-再捕获数据集进行年龄别生存分析。它不但能够对生存参数，捕获概率，以及未知的出生和死亡时间进行估计，还允许用户测试一系列不同的生存模型。

在实际操作中，首先需要在R软件中安装BaSTA包，程序如下：

install.packages(“BaSTA”)；library(BaSTA)

实际操作BaSTA包主要从以下几个步骤考虑:

(1) 数据读取：读取需要进行年龄别生存分析的数据集

data <- read.table(“location of the data set.txt”,sep=“ ”,header=TRUE)

读取的数据集需具备表1的组织形式。

其中，每一行对应于一个个体，且用ID作为唯一的身份识别标志。对于每一个个体，若可以明确获知其出生或者死亡的时间，就在出生时间列和死亡时间列记录具体的年份，若无法获知，就记为0。在捕获-再捕获实验中，假设捕获周期的数量为T，时间间隔为1年，那么时间1，时间2，…，时间T分别表示实验开始的第1年，第2年，…，第T年。若个体在该时间被捕获到了就记为1，否则就记为0。这组长度为T的数据构成了个体的捕获历史。

表1 导入数据的格式

(2) 模型选择：选择用于数据集分析的生存模型

multiout<- multibasta(data,studyStart,studyEnd,

models=c(“EX”,“GO”,“WE”,“LO”),

shapes=c(“simple”,“Makeham”,“bathtub”))

studyStart和studyEnd分别表示捕获-再捕获实验开始和结束的时间。

BaSTA包提供了四个基本的models(生存模型)，分别为：(a)Exponential，(b)Gompertz，(c)Weibull和(d)Logistic。每个模型所描述的年龄别死亡率和生存率具有不同的走向趋势。此外，BaSTA包还允许用户对这些基本模型进行扩展，从而具有更加复杂的模型形式。具体而言，就是定义了三种shapes形式：(a)simple，仅使用上述基本模型的死亡率函数；(b)Makeham，向函数中添加一个常数；(c)bathtub，向函数中添加一个常数和一个减小的Gompertz函数。其中，Exponential模型仅能与simple形式相组合。因此，BaSTA包总共包含了10种组合生存模型，具有相当大的灵活性。选择哪一种生存模型来进行分析，可以利用偏差信息准则(deviance information criterion，DIC)[3]和相关的统计量来对模型的拟合程度和复杂程度进行评价。

multibasta()函数允许用户在同一数据集上运行具有不同函数形式的模型，进行模型比较并可视化输出运行的结果。如果模型的所有参数都已经收敛，那么BaSTA包会计算出DIC值。一般情况下，选择DIC值较小的模型。

(3) 模型拟合：用选择的生存模型对数据集进行拟合，并且估计参数值

fit<- basta(data,studyStart,studyEnd,minAge,model,shape,niter,burnin,thinning,nsim,…)

其中，minAge表示年龄别生存分析的起始年龄，niter表示MCMC算法迭代的次数，burnin表示删除的初始迭代的次数，thinning表示为了减小自相关所跳过的MCMC步骤数，以及nsim表示运行的模拟链数目。

(4) 结果输出：输出参数估计值，并绘制相关曲线

summary(fit)

plot(fitt,plot.trace)

summary()函数可查看模型拟合后的结果，包括参数的估计值，以及相对应的标准差等。plot()函数可以绘制相关的曲线图。若plot.trace=FALSE，则绘制种群的年龄别死亡率和生存率曲线图；若plot.trace=TRUE，则绘制出生存参数的迭代过程。

实例分析

1.数据来源

本文数据来源于2007年1月至2015年12月上海曙光医院住院部肠癌患者的就诊记录。一共搜集到原始数据33118条。将搜集到的数据用病人的患者主索引号(EMPI)作为唯一的身份识别标志，且以12个月为一个捕获周期，借助Python软件对原始数据进行处理。整理得到2050例肠癌患者的捕获-再捕获数据，其中仅有151例可以明确地获知死亡年龄。一共有女性患者924例，男性患者1126例；直肠癌患者为932例，结肠癌患者为939例，其他肠癌患者为179例。

2.数据分析

由于所获得的数据中，年龄小于30岁的住院患者样本数目较少，故本次年龄别生存从最小年龄30岁开始进行。

(1) 肠癌患者整体年龄别生存分析

根据multibasta()函数运行的结果，选择Gompertz函数[4]来对肠癌患者的整体数据进行拟合，则年龄别死亡率函数可以表示为μb(x|b)=eb0+b1x，相对应的生存函数可以表示为Sb(x|b)=exp[eb0(1-eb1x)/b1]。其中，eb0表示初始死亡率，b1表示死亡率随着年龄呈指数增长的速度。假定捕获概率随时间而变化，构造两条马尔科夫链，且各自迭代40000次。运行程序如下：

fit <-basta(data,studyStart=2007,studyEnd=2015,minAge=30,

model=“GO”,shape=“simple”,

niter=40000,burnin=20000,thinning=50,

nsim=2)

程序运行之后，得到的生存模型的参数迭代过程如图1所示。从图中可以观察到，两条马尔科夫链最后收敛于同一值。去掉最开始的20000次迭代后，得到的参数估计值分别为b0=-5.30105，b1=0.04982，对应的标准差分别为0.141918，0.003668，可信水平95%下的可信区间分别为(-5.59110，-5.05633)，(0.04340，0.05695)。由于参数的标准差都很小，且可信区间都很短，即波动性很小，因此参数的估计是合理的。肠癌患者的年龄别死亡率和生存率曲线如图2和图3所示。

图1 肠癌患者整体生存模型参数的迭代过程

图2 肠癌患者整体年龄别死亡率曲线图

图3 肠癌患者整体年龄别生存率曲线图

(2) 不同性别年龄别生存分析

选择Gompertz函数来对女性肠癌患者的数据进行拟合，得到的参数估计值为b0=-5.39197，b1=0.05283，对应的标准差分别为0.178862，0.004184，可信水平95%下的可信区间分别为(-5.72823，-5.01510)，(0.04465，0.06090)。经检验，参数的估计是合理的。

不同性别的年龄别死亡率和生存率曲线分别如图4和图5所示。其中实线代表为女性患者，虚线代表男性患者。

图4 不同性别肠癌患者的年龄别死亡率曲线图

图5 不同性别肠癌患者的年龄别生存率曲线图

(3) 直肠和结肠癌患者年龄别生存分析

选择logistic函数加上Makeham形状的组合模型来对结肠癌患者的数据进行拟合，得到的参数估计值为c=0.009167，b0=-6.037297，b1=0.060407，b2=0.159034，对应的标准差分别为0.004261，0.621924，0.011753，0.136671，可信水平下的95%可信区间分别为(0.00122，0.01725)，(-7.10853，-4.50925)，(0.033934，0.08072)，(0.00588，0.50675)。 经检验，参数的估计是合理的。

直肠和结肠癌患者的年龄别死亡率和生存率曲线如图6和图7所示。其中实线代表为直肠癌患者，虚线代表结肠癌患者。

图6 不同患癌部位肠癌患者的年龄别死亡率曲线图

图7 不同患癌部位肠癌患者的年龄别生存率曲线图

3.结论分析

肠癌患者整体死亡率随着年龄的增长而增长，其死亡中位年龄为71.55岁。不同性别肠癌患者的死亡率均随着年龄的增长而增长，其中男性患者的年龄别死亡率高于女性患者，这与李德錄[7]，王宁[8]等人得到的结论相同。死亡中位年龄分别为女性71.65岁，男性69.25岁。

不同患癌部位的肠癌患者死亡率均随着年龄的增长而增长，其中大约在60岁之前，直肠癌患者的年龄别死亡率低于结肠癌患者，在60岁之后，直肠癌患者的年龄别死亡率高于结肠癌患者，得到的结果与李德錄[7]大致相同。死亡中位年龄分别为直肠癌71.25岁，直肠癌68.05岁。

本文通过实例介绍了R软件BaSTA包在贝叶斯框架下，对捕获-再捕获数据集进行年龄别生存分析的方法。借助该包对患者进行生存分析，可有效分析现有的临床医学数据，给出患者的生存参数估计值，并进行可视化展示，具有广泛的应用价值。